基于疲劳试验的车轮拓扑优化和多目标优化∗
2018-01-15王登峰
王登峰,张 帅,陈 辉,汪 勇
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
前言
车轮是汽车行驶系中最重要的承载件和安全件,属于非簧载质量,其轻量化程度和综合性能优劣直接影响汽车的经济性、动力性、操纵性、平顺性、制动性和行车安全[1]。
自文献[2]中提出拓扑优化的均匀化方法以来,拓扑优化方法在结构优化设计中得到了深入发展和广泛应用[3-6]。文献[7]中对铝合金车轮进行了拓扑优化,并仿真分析了优化后车轮的强度和刚度。文献[8]中以轮辋和轮缘厚度为设计变量、弯曲疲劳和径向疲劳工况的车轮最大应力为约束、车轮质量最小为目标,对铝合金车轮进行了优化。文献[9]中基于弯曲疲劳试验对钢制车轮进行了多目标拓扑优化,以柔度和模态频率为目标对车轮进行轻量化设计,并进行了车轮应力分析和试验验证。
国内外学者在车轮疲劳试验的仿真分析上取得了很多成果。文献[10]中采用ANSYS对铝合金车轮弯曲疲劳寿命进行了预测。文献[11]中对钢制车轮冲压过程进行了仿真分析和试验验证,提取了冲压残余应力,研究了残余应力对车轮弯曲疲劳寿命的影响。文献[12]中通过材料拉伸试验得到A356-T6铝合金车轮的S-N曲线,仿真分析了车轮的弯曲疲劳寿命和应变并进行了试验验证。文献[13]中通过仿真分析研究了充气压力对铝合金车轮冲击试验和径向载荷试验车轮应力的影响。文献[14]中研究了轮胎参数在径向疲劳试验仿真分析中的作用,结果表明轮胎竖直刚度对车轮径向疲劳寿命有重要影响。文献[15]中基于弯曲疲劳和径向疲劳试验的车轮受力状况,对镁合金车轮进行了强度和模态分析。
在疲劳寿命的计算和优化方面,文献[16]中模拟了铝合金车轮的低压铸造,进行了疲劳寿命和冲击试验的简化仿真分析,实现了工艺过程模拟与结构有限元模拟的仿真技术集成。文献[17]中采用ANSYS计算了弯曲疲劳试验下镁合金车轮的应力,对S-N曲线进行插值计算得出疲劳寿命,以轮辋和轮辐的厚度为设计变量对车轮进行了轻量化设计。文献[18]中建立了铝合金车轮弯曲疲劳和径向疲劳试验的有限元模型,使用FE-SAFE软件预测车轮疲劳寿命,用试验验证了有限元方法预测寿命的可行性。此外,国内外学者在车轮试验与仿真对比和新材料的应用上也进行了研究[19-23]。
但是,以上研究多集中在疲劳试验的仿真分析和试验验证上;在优化设计中将疲劳寿命仅用作检验和校核优化后的车轮,而不是直接作为约束条件;车轮轻量化设计时没有建立参数化车轮模型,而是在参数化阶段设置多组模型进行对比或者仅将车轮厚度作为设计变量,极大地影响了车轮结构的变形能力,从而使优化空间和效果有限。同时,以上优化设计没有兼顾车轮概念设计阶段的拓扑优化和参数化阶段的多目标优化;所研究的车轮均为单一材料的整体式结构,没有研究异种材料的组装式车轮。
因此,本文中基于车轮疲劳试验提出了一种联合拓扑优化方法,设计了一个16×6J型的组装式车轮。将组装式车轮的强度、刚度、疲劳寿命和径向疲劳寿命安全系数等综合性能参数直接作为优化设计指标,提升了车轮性能和优化空间;利用网格变形技术建立了组装式车轮在弯曲和径向疲劳试验工况下的参数化模型,提升了车轮的变形能力,实现了高精度的实验设计采样和近似模型拟合,通过多目标优化实现了与车轮概念设计和参数化设计的协同优化以及同时考虑多种性能的车轮轻量化设计。
1 组装式车轮建模
1.1 基于弯曲疲劳试验工况的轮辐拓扑优化设计
(1)试验工况

图1 车轮概念设计模型
根据GB/T 5334—2005《乘用车车轮性能要求和试验方法》,车轮应满足动态弯曲疲劳试验要求,试验方法如图2所示。

图2 车轮动态弯曲疲劳试验示意图
试验时在加载轴末端施加力F产生弯矩,车轮在恒定的弯矩作用下旋转,达到10万次循环前车轮不能出现新可见裂纹,加载点偏移量不能超过初始全加载偏移量的20%。
取加载轴长度L=0.9m。试验弯矩M和加载力F分别为

式中:μ为轮胎与路面间的摩擦因数;R为轮胎静负荷半径,m;d为车轮偏距,m;Fv为车轮最大垂直静负荷,N;S为强化试验因数。
结合车轮型号,试验参数确定如下:μ=0.7,R=0.316m,d=0.053m,Fv=6027N,S=1.6。 由式(1)和式(2)算得M=2644N·m,F=2938N。
(2)车轮拓扑优化建模
将车轮的概念设计模型导入HyperMesh中进行几何清理,并采用四面体单元进行网格划分。其中,轮辋单元大小为4mm,轮辐拓扑空间单元大小为5mm,加载轴单元大小为10mm,允许最小尺寸均为2mm。按照车轮动态弯曲疲劳试验方法要求,约束轮辋内侧外沿节点的全部自由度,在加载轴末端施加2 938N的力。轮辋、轮辐和加载轴分别赋予镁合金AZ80、铝合金A356和A3钢的材料属性。各材料参数如表1所示,建立的车轮拓扑优化有限元模型如图3所示。
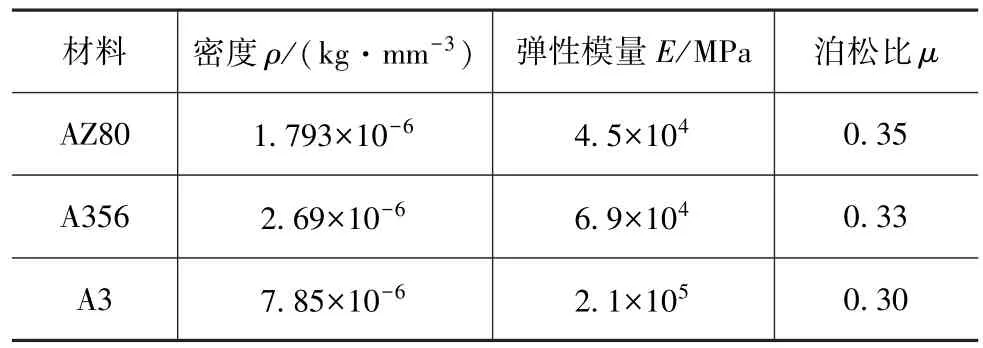
表1 材料参数

图3 车轮弯曲疲劳工况拓扑优化模型
有限元分析时,使用材料的屈服许用应力作为应力约束来保障车轮的疲劳寿命,镁、铝合金的安全因数s取1.2来计算屈服许用应力,材料属性见表2。
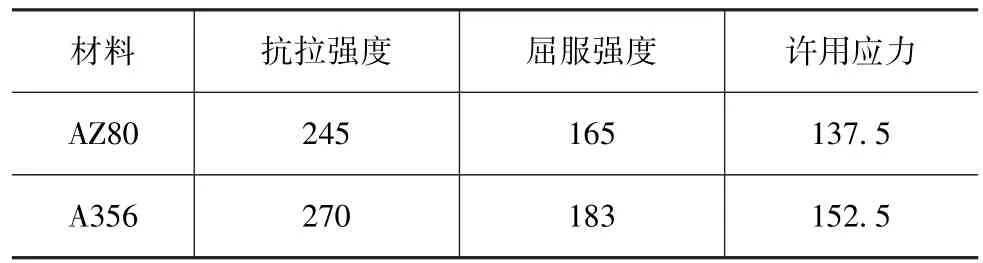
表2 镁、铝合金材料属性 MPa
(3)车轮拓扑优化设计
采用Optistruct进行拓扑优化。为模拟弯曲疲劳试验时载荷的动态变化,添加周向对称约束[26]。为模拟车轮的锻压工艺,添加拔模约束。为清晰显示拓扑优化结果中的材料分布,添加最小密度单元约束,约束单元最小尺寸为2mm。约束车轮的强度和刚度,车轮强度用许用应力约束,车轮刚度通过车轮节点的最大偏移量约束。以车轮单元密度为设计变量,最大Von Mises应力、节点最大偏移量为约束条件,质量最小为目标函数进行拓扑优化。拓扑优化的数学模型为

式中:m(ρ)为车轮质量,kg;σb(ρ)为轮辐弯曲载荷下的最大 Von Mises应力,MPa;σd为轮辐许用应力,MPa,σd=152.5MPa;D(ρ)为车轮节点最大偏移量,mm;D0为车轮节点许用偏移量,mm,D0=0.8mm;ρ为单元密度,kg/mm3。
当单元密度为0.3kg/mm3时,5辐和6辐车轮的拓扑优化结果如图4所示。

图4 车轮弯曲疲劳工况拓扑优化结果
车轮的材料分布由内部的应力传递路径决定,材料密度与应力值有关。加载轴的弯矩沿着车轮螺栓孔向轮辐传递,而且其产生的应力依次递减,这决定了车轮的材料分布和密度。依据拓扑优化结果,5辐车轮结构最优,这是由车轮安装面的螺栓孔个数决定的。
1.2 基于径向疲劳试验工况的轮辐拓扑优化设计
(1)试验工况
根据GB/T 5334—2005,车轮应满足动态径向疲劳试验要求,试验方法如图5所示。
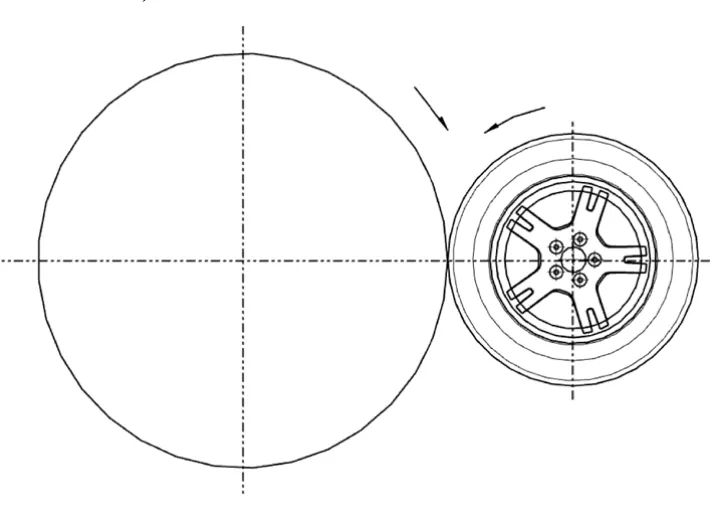
图5 车轮动态径向疲劳试验示意图
图中车轮在试验台上转动时,转鼓向其传递径向负荷Fr,在循环50万次前车轮不能出现新的可见裂纹。
车轮的径向负荷Fr为

式中:Fv为车轮最大垂直静负荷,N;K为强化试验因数。
结合车轮型号,试验参数确定如下:Fv=6027N,K=2.25。 根据式(4),算得 Fr=13561N。 轮辋外表面所受充气压力选为0.45MPa。
车轮的径向负荷通过轮胎对称加载在轮辋两侧的胎圈座上,并在2θ0角度内成余弦分布。在此需要说明的是,根据力学原理,两个接触物体之间的相互作用力是沿着表面法向的,因此,胎圈对胎圈座的分布压力理应沿着径向,但公式推导过程发现这样的计算比较复杂。鉴于分布压力采用余弦规律分布本身就是一个近似的假设,故为简化计算,参照文献[27],将分布压力简化为沿垂向施加,如图6所示。

图6 车轮径向加载示意图
在图6中设立柱坐标系,设单侧胎圈座受力为F,加载处半径为rb,加载面的宽度为B,单个加载压力为A,与竖直方向夹角为θ,则加载压力的余弦振幅A0推导如式(5)和式(6)。
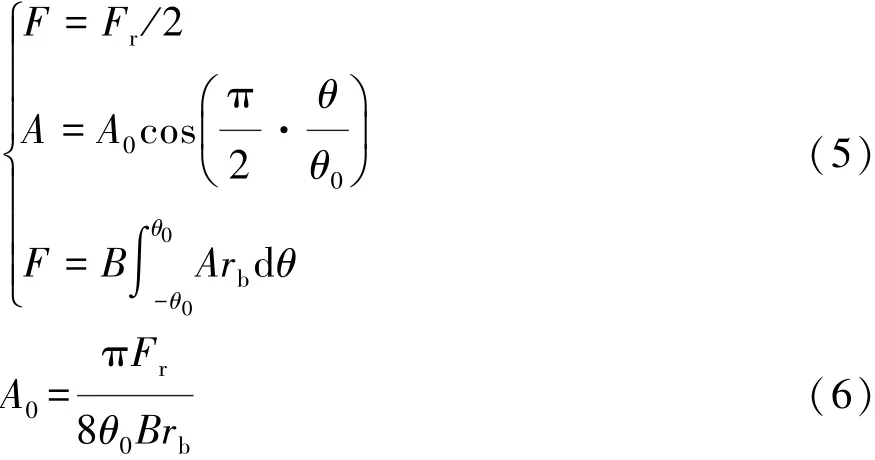
(2)车轮拓扑优化建模
在HyperMesh中对车轮拓扑优化模型采用四面体单元进行网格划分。其中,轮辋单元大小为4mm,轮辐单元大小为5mm,允许最小尺寸均为2mm。轮辋和轮辐分别赋予镁合金AZ80和铝合金A356的材料属性。按照车轮动态径向疲劳试验方法要求,约束车轮安装面上5个螺栓孔的全部自由度,胎圈座2θ0内加载振幅为1.88MPa的余弦压力,两胎圈座之间的轮辋外表面上加载0.45MPa的充气压力。拓扑优化有限元模型如图7所示。

图7 车轮径向疲劳工况拓扑优化模型
(3)车轮拓扑优化
在优化设计中,把刚度增大问题等效为柔度减小问题来研究,柔度则用应变能来定义[28-29]。多个工况的柔度加权和即为加权柔度,如式(7)所示。
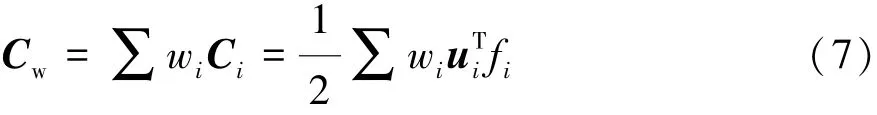
式中:Cw为加权柔度,N·mm;wi为各工况的柔度权重,取值0~1;Ci为第 i个工况的柔度,N·mm;uT
i为位移矩阵的转置矩阵;fi为第i个工况的载荷,N。
采用Optistruct进行拓扑优化,添加周向对称约束、拔模约束、单元最小尺寸为2mm等约束。以车轮单元密度为设计变量,最大Von Mises应力、加权柔度为约束条件,质量最小为目标函数。拓扑优化数学模型为
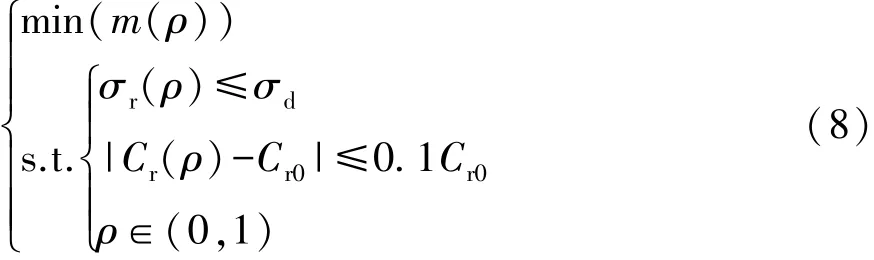
式中:m(ρ)为车轮质量,kg;σr(ρ)为轮辐径向载荷下的最大 Von Mises应力,MPa;σd为轮辐许用应力,MPa,σd=152.5MPa;Cr(ρ)为车轮径向载荷下的加权柔度,N·mm;Cr0为柔度许用值,N·mm,Cr0=3820N·mm。
当单元密度为0.3时,5辐和6辐车轮的拓扑结果如图8所示。
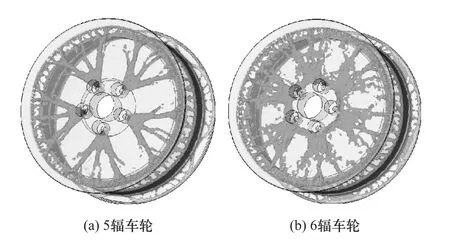
图8 车轮径向疲劳工况拓扑优化结果
径向疲劳试验时,因为轮辋表面受均匀气压,所以轮辋和轮辐交接处的材料密度分布均匀,在设计组装式车轮时此处可以设计成圆环。同时,胎圈座承受了在2θ0角度内成余弦分布的径向负荷,所以轮辐材料沿着安装面螺栓孔向轮辋扩散分布。拓扑优化结果由安装面螺栓孔的个数和径向负荷分布角度2θ0决定,5辐和6辐车轮结构均优。
1.3 联合两种工况的轮辐拓扑优化设计
根据第1.1和1.2节的拓扑优化结果,采用Optistruct对车轮进行联合拓扑优化设计。单元密度为0.3kg/mm3时,5辐和6辐车轮的拓扑结果如图9所示。
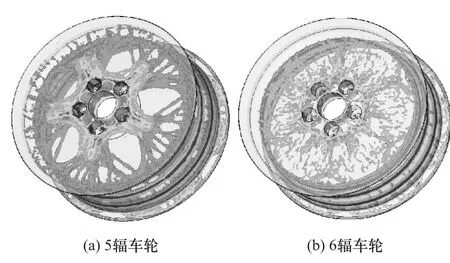
图9 车轮联合拓扑优化结果
联合拓扑优化设计时,车轮内部应力传递既包含了弯矩的传递路径,又兼顾了径向负荷的分布角度等因素,材料分布更加合理。如图9所示,5辐车轮结构最优,选择该结构对车轮进行建模。
1.4 组装式车轮结构设计
采用HyperView,将联合拓扑优化的5辐车轮结构导出三维几何模型。参照该模型尺寸,在UG中建立拓扑优化后的组装式车轮模型,如图10所示。
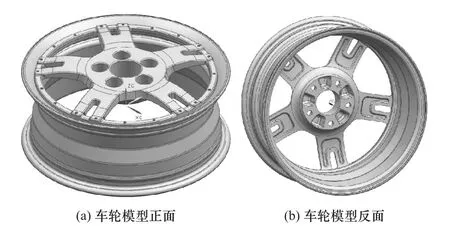
图10 组装式车轮模型
2 组装式车轮弯曲疲劳性能分析
2.1 有限元建模
按1.1节(2)的前处理方法,对组装式车轮模型进行前处理。共离散为389 445个单元和108 858个节点,有限元模型如图11所示。
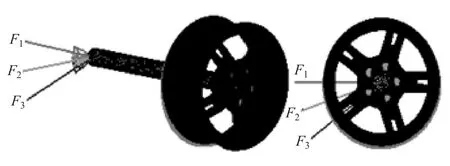
图11 车轮弯曲疲劳试验有限元模型
如图11所示,力F设置3个加载方向,分别为F1,F2和 F3,夹角为 18°,模拟范围为 36°,是车轮受力对称周期的。其中:F正对窗口,F在中间位12置,F3正对辐条。轮辋和轮辐之间的螺栓连接用rbe2模拟。
2.2 强度分析
运用MSC.Nastran进行强度计算,结果如图12所示。
由图12可见,轮辐在F3时产生最大应力,为132.92MPa,发生在轮辐背面根部减重处;轮辋在F1时产生最大应力,为107.02MPa,发生在轮辋与轮辐连接的螺栓孔处;在F2时轮辐根部的节点产生最大位移0.48mm。轮辐和轮辋的应力均小于其许用应力,该设计满足强度要求;车轮节点的最大偏移量小于其许用值0.8mm,该设计满足刚度要求。

2.3 疲劳寿命分析
车轮的疲劳失效通常为低载高周疲劳损伤,采用名义应力法(S-N法)进行疲劳寿命分析。该方法通过S-N曲线将疲劳寿命和应力之间的关系定义为

式中:σa为真实循环应力幅,MPa;σf′为疲劳强度因数;Nf为以循环数计的疲劳寿命;b为疲劳强度指数。
基于Palmgren-Miner线性疲劳损伤累积理论,变幅载荷下部件的疲劳损伤和疲劳寿命定义为

式中:D为疲劳损伤;k为变幅载荷的应力水平级数;ni为第i级载荷的循环次数;Nfi为第i级载荷下的疲劳寿命。
本文中载荷正弦变化,是对称恒幅循环载荷。根据式(10),车轮的疲劳损伤和疲劳寿命定义为

式中:n为载荷的循环次数;N为疲劳寿命。
材料S-N曲线,通过式(12)定义:

式中:S为应力;m和C为与材料、应力比和加载方式等有关的参数。
AZ80和A356材料的S-N曲线如图13所示。
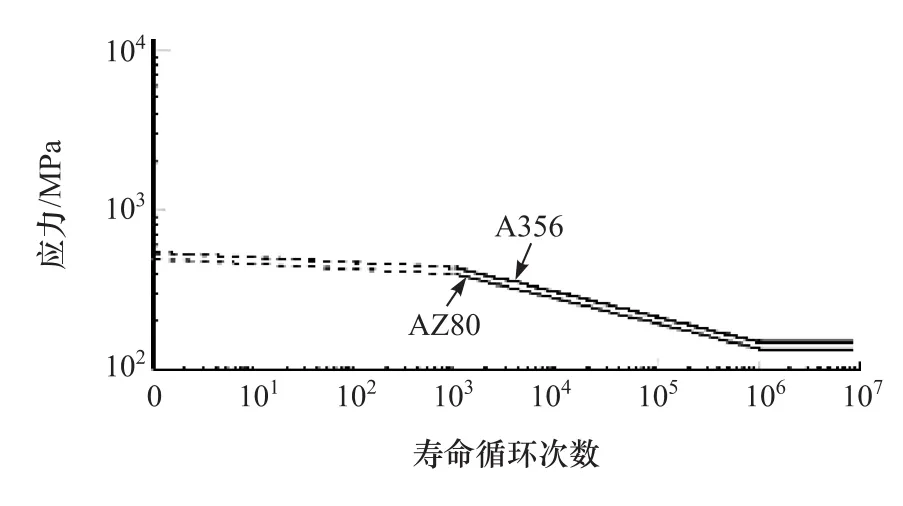
图13 AZ80和A356的S-N曲线
基于上述方法,在MSC.Fatigue软件中进行疲劳寿命计算。设置存活率为96%,应力组合方式为Von Mises,载荷时间历程曲线为正弦函数,不进行平均应力修正。分别以轮辋和轮辐应力最大的工况1和工况3进行计算,得到的车轮疲劳寿命云图分别如图14和图15所示。

图14 工况1车轮疲劳寿命云图

图15 工况3车轮疲劳寿命云图
车轮在工况3下疲劳寿命最低,轮辐在正面开槽处寿命较低,在背面根部减重处的寿命最低,为15.4万次,满足弯曲疲劳寿命要大于10万次的要求。轮辋寿命为1020次,属于无限寿命,满足寿命要求。车轮结构有进一步优化的空间。
3 组装式车轮径向疲劳性能分析
3.1 有限元建模
按1.2节(2)的前处理方法,对组装式车轮模型进行前处理。共离散为362 600个单元和102 398个节点,有限元模型如图16所示。
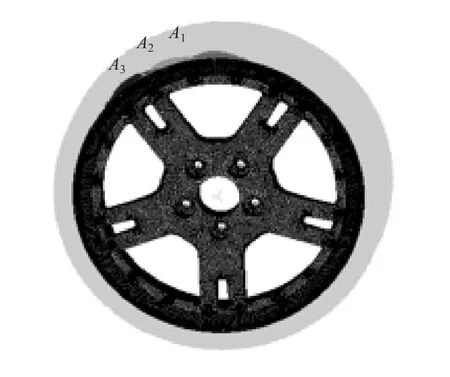
图16 车轮径向疲劳试验有限元模型
余弦压力A的加载位置设置为3处,分别为A1,A2和 A3,夹角为 18°,模拟范围为 36°,是车轮受力对称周期的。其中:A正对窗口,A在中间位置,A123正对辐条。轮辋和轮辐之间的螺栓连接用rbe2模拟。
3.2 强度分析
运用MSC.Nastran进行计算,结果如图17所示。
由图17可见,轮辐和轮辋均在A2时产生最大应力,分别为70.07和43.99MPa;轮辐最大应力发生在背面中部减重处,轮辋最大应力发生在胎圈座余弦压力最大值加载处;但应力远小于其许用应力,车轮满足强度要求。车轮节点在A3时产生最大位移为1.03mm;在远离辐条的加载处轮辋节点偏移量最大,此偏移量只定性分析径向疲劳试验时车轮的刚度,定量分析时采用车轮加权柔度表征。
3.3 疲劳寿命及其安全系数分析
基于2.3节所述方法,采用MSC.Fatigue软件进行疲劳寿命计算。设置存活率为96%,应力组合方式为Von Mises,载荷时间历程曲线为正弦函数,不进行平均应力修正。以工况2进行计算,得到的车轮疲劳寿命云图如图18所示。
由图可见,车轮寿命达1020次,属于无限寿命,满足径向疲劳寿命要大于50万次的要求。
对于无限寿命部件,需要研究其疲劳寿命安全系数来评价其疲劳损伤情况。采用MSC.Fatigue软件对车轮进行疲劳寿命安全系数计算,结果如图19所示。

图17 车轮应力和节点位移云图
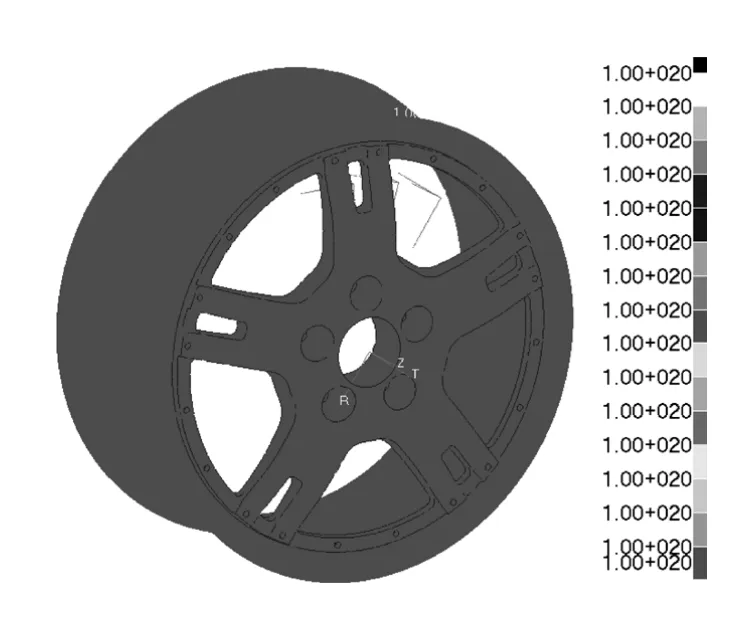
图18 工况2车轮疲劳寿命云图

图19 工况2车轮疲劳寿命安全系数云图
由图可见,轮辋内侧和余弦压力加载处辐条的疲劳寿命安全系数最小,为1.87,但仍满足安全系数大于1.5的要求,车轮结构有进一步优化的空间。
4 组装式车轮多目标优化
4.1 组装式车轮参数化建模
为研究车轮结构与性能的关系,并对车轮进行多目标优化设计,需要对车轮模型进行参数化[30-31]。
基于网格变形技术,采用DEP-MeshWorks软件分别对弯曲疲劳试验和径向疲劳试验工况有限元模型中的车轮进行参数化,建立组装式车轮的参数化模型,定义10个厚度变量和2个形状变量(设为x1,x2,…,x12),如图20所示。各设计变量和取值范围如表3所示。
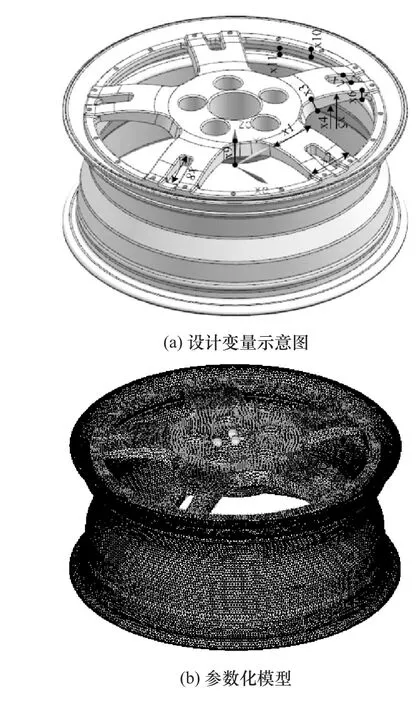
图20 车轮设计变量及参数化模型
4.2 近似模型的建立
为提高优化效率,使用近似模型进行多目标优化[32]。采用Kriging近似模型代替仿真模型来表达各设计变量和各性能指标之间的关系[33-34]。根据每个设计变量的取值范围,使用Hammersley试验设计方法在两个有限元模型中分别选取72个样本点拟合各性能指标的Kriging近似模型。使用决定系数R2检验近似模型的精度[35],其表达式为
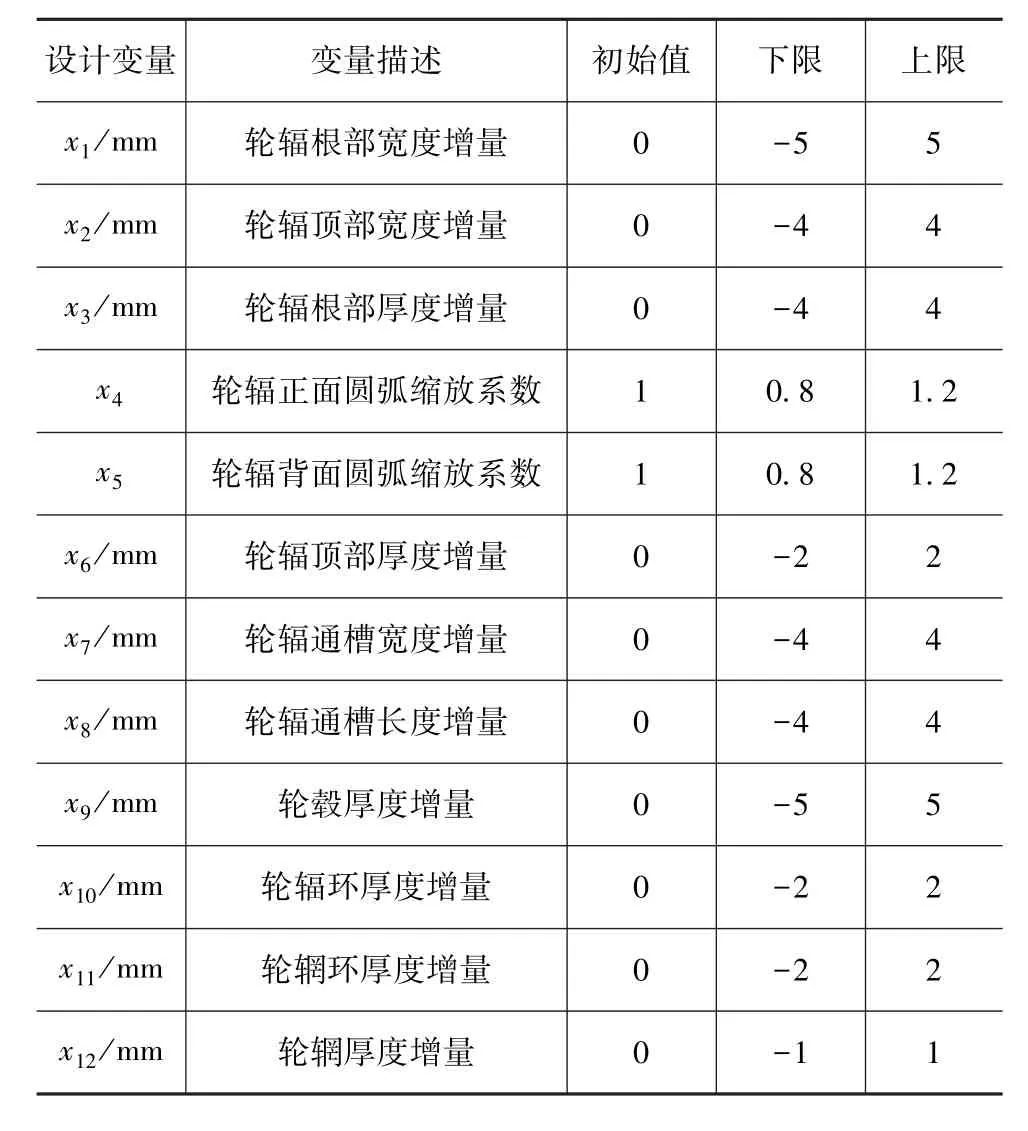
表3 各设计变量及取值范围
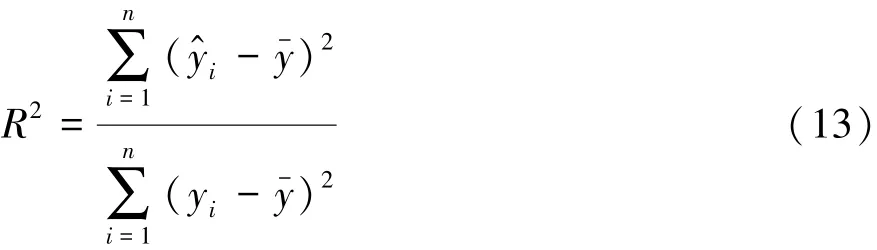
式中:n为样本点数量;y^i为第i个响应的近似模型预测值;y-为平均值;yi为第i个响应的仿真值。
R2的值越逼近100%,则近似模型的拟合精度越高。采用最优拉丁超立方设计另外选取10个样本点检验近似模型精度,得到各性能指标的决定系数R2值均大于95%,满足近似模型拟合精度要求。部分性能指标的近似模型精度检验结果如图21所示。
4.3 多目标优化
综合考虑车轮质量、强度、刚度、疲劳寿命和径向疲劳安全系数等性能指标,对组装式车轮进行多目标优化,优化数学模型为

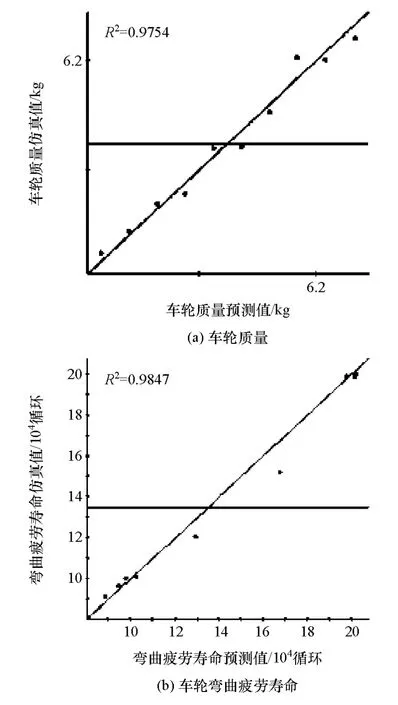
图21 部分性能指标的近似模型精度
式中:m(x)为多目标优化中的车轮质量,kg;Nb(x)为车轮动态弯曲疲劳寿命,104循环;sN(x)为车轮动态径向疲劳寿命的安全系数;σbd和σrd分别为弯曲和径向工况下轮辐最大Von Mises应力,MPa;σbr和σrr分别为弯曲和径向工况下轮辋最大Von Mises应力,MPa;σd0和σr0分别为轮辐和轮辋的屈服应力,σd0=183MPa,σr0=165MPa;Db(x)和 Db0分别为弯曲工况下车轮节点的最大位移和许用位移值,Db0=0.8mm;Cr(x)和Cr0分别为径向工况下车轮的柔度和许用值,Cr0=3800N·mm;Nr(x)和Nr0分别为车轮动态径向疲劳寿命和许用值,104循环;Nr0=50×104循环;x为设计变量;xL和xU分别为设计变量取值的下限和上限。
使用Isight软件集成各性能指标的计算组件,选取第二代非劣排序遗传算法(NSGA-Ⅱ),建立基于Kriging近似模型的组装式车轮多目标优化设计模型,如图22所示。
4.4 优化结果分析
经过8 002次迭代,优化得到的Pareto前沿如图23所示。
由图23可知,车轮质量、弯曲疲劳寿命和径向疲劳寿命安全系数这3个目标的Pareto前沿的变化是复杂的、非同步的。主要因为这3个目标是矛盾的,此外,在设计变量中不仅有厚度变量,还有形状变量,而且两者之间又相互转化,这些原因共同决定了3个目标的Pareto解的复杂性,需要根据设计需求从Pareto解集中选择Pareto解。以车轮质量和径向疲劳寿命安全系数为优先考虑,在Pareto前沿中选取一个妥协解,如图23中箭头所指。优化前后各设计变量和各性能指标的对比分别如表4和表5所示。

图22 车轮多目标优化设计模型
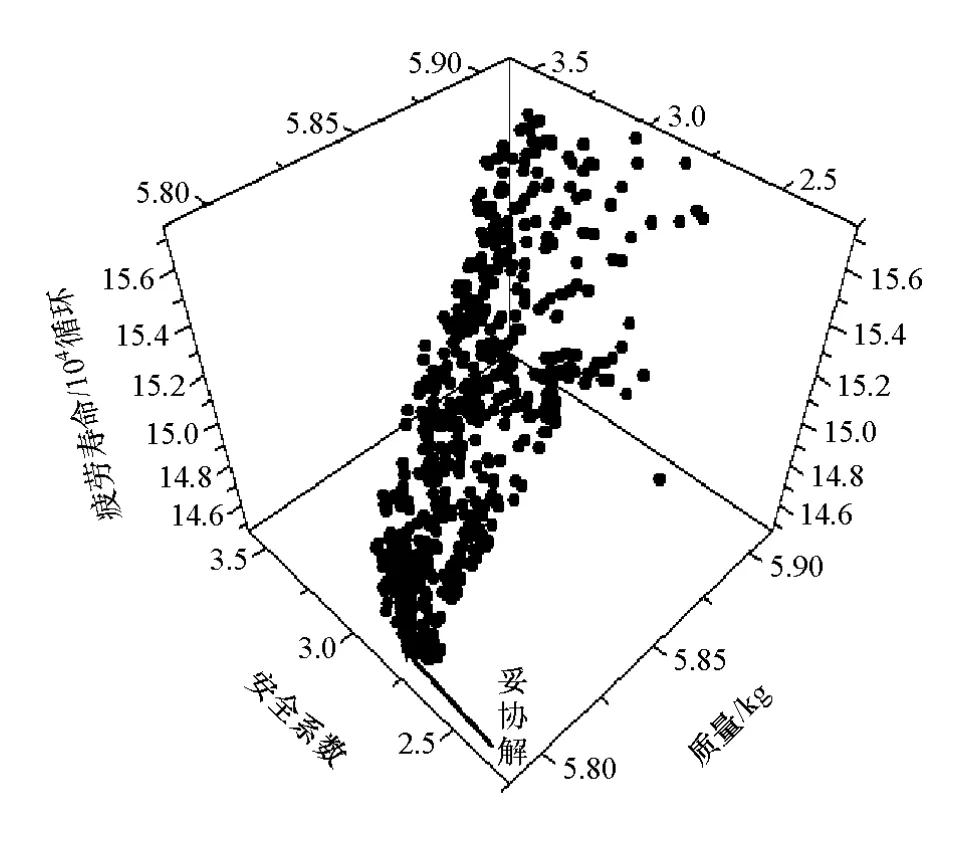
图23 Pareto前沿

表4 优化前后设计变量取值

表5 优化前后各性能值对比
由表5可见,通过NSGA-Ⅱ算法对Kriging近似模型进行迭代优化,使得车轮质量比拓扑优化后的质量降低了6.44%,弯曲疲劳寿命降低了5.84%,径向疲劳寿命安全系数提高了50.80%。其中,车轮径向疲劳寿命在优化前后均为无限寿命,各项性能指标均满足设计要求。与市场上某同型号铸造铝合金整体式车轮质量8.213kg相比,本文中优化设计的组装式车轮质量减小2.417kg,降低29.42%。
5 结论
(2)综合考虑了两种工况下车轮内部应力的传递路径和应力值,对车轮进行了联合拓扑优化,得到了轮辐拓扑结构和材料密度云图,设计了一个镁合金轮辋、铝合金轮辐并通过螺栓连接的组装式车轮。
(3)建立了组装式车轮在动态弯曲疲劳试验和动态径向疲劳试验工况下的有限元模型,分析了两种工况下车轮的强度和疲劳寿命,以及径向疲劳试验工况下车轮疲劳寿命的安全系数等性能参数,研究了各性能与车轮结构的关系。
(4)基于网格变形技术建立了两种工况下车轮的参数化模型,综合运用DOE采样、近似模型理论和NSGA-Ⅱ算法,对组装式车轮进行了多目标优化设计,得到了Pareto前沿。在综合考虑并满足了车轮各项性能的条件下选取了一个妥协解,并对比分析了优化前后车轮各性能指标的变化,结果表明:相对于同型铸造铝合金整体式车轮,本组装式车轮减重29.42%。
(5)通过对车轮的拓扑优化、疲劳试验性能的仿真分析和参数化建模,实现了一套基于车轮疲劳性能的结构设计流程和优化方法,为车轮多目标优化设计提供了理论和技术依据。
[1] SONGW,WOODS JL,DAVISR T,et al.Failure analysis and simulation evaluation of an al 6061 alloy wheel hub[J].Journal of Failure Analysis and Prevention,2015,15(4):521-533.
[2] BENDSØE M P, KIKUCHI N.Generating optimal topologies in structural design using a homogenization method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(2):197-224.
[3] DEATON JD,GRANDHIR V.A survey of structural and multidisciplinary continuum topology optimization:post2000[J].Structural and Multidisciplinary Optimization,2014,49(1):1-38.
[4] JEONG SH,YOON G H,TAKEZAWA A,et al.Development of a novel phase-fieldmethod for local stress-based shape and topology optimization[J].Computers & Structures,2014,132:84-98.
[5] SANGREER,CARSTENSEN JV,GAYNOR A T,etal.Topology optimization as a teaching tool for undergraduate education in structural engineering[C].Structures Congress 2015.2632-2642.
[6] LIU J,MA Y.A survey ofmanufacturing oriented topology optimization methods[J].Advances in Engineering Software,2016,100:161-175.
[7] ZHANG Z J,JIA H L,SUN JY,et al.Application of topological optimization on aluminum alloy automobile wheel designing[C].Advanced Materials Research.Trans Tech Publications,2012,562:705-708.
[8] HU JH,LIU X X,SUN H X,et al.Development and application of light-weight design of the aluminum alloy wheel[C].Applied Mechanics and Materials.Trans Tech Publications, 2013, 310:253-257.
[9] XIAOD,ZHANGH,LIU X,etal.Novel steelwheel design based on multi-objective topology optimization[J].Journal of Mechanical Science and Technology,2014,28(3):1007-1016.
[10] 韩兵,朱茂桃,张永建.铝合金车轮动态弯曲疲劳寿命预测[J].农业机械学报,2008,39(5):208-210.
[11] SHANG D,LIU X,SHAN Y,etal.Research on the stamping residual stress of steelwheel disc and its effecton the fatigue life of wheel[J].International Journal of Fatigue,2016,93:173-183.
[12] BALLO F,FRIZZIR,MASTINU G,et al.Lightweight design and construction of aluminum wheels[C].SAE Paper 2016-01-1575.
[13] 闫胜昝,童水光,朱训明.轮胎充气压力对车轮应力分布影响的数值模拟[J].浙江大学学报(工学版),2009,43(3):565-569.
[14] OERY T, SANKARAN R T,NESARIKAR A S.Simulation and test correlation ofwheel radial fatigue test[C].SAE Paper 2013-01-1198.
[15] 郑松林,郑钻玺,徐洪慧,等.汽车镁合金车轮动态特性分析[J].汽车工程,2011,33(2):148-151.
[16] 张响.铝合金车轮数字化仿真及工艺优化[D].杭州:浙江大学,2008.
[17] 周渝庆.镁合金车轮疲劳寿命预测与优化设计[D].重庆:重庆大学,2008.
[18] 尤金艳.基于弯曲与径向疲劳试验的铝合金车轮有限元分析[D].广州:华南理工大学,2013.
[19] FIRATM,KOZANR,OZSOYM,etal.Numericalmodeling and simulation ofwheel radial fatigue tests[J].Engineering Failure A-nalysis,2009,16(5):1533-1541.
[20] WAN X,SHAN Y,LIU X,etal.Simulation of biaxialwheel test and fatigue life estimation considering the influence of tire and wheel camber[J].Advances in Engineering Software,2016,92:57-64.
[21] TIWARID, ARORA J, KHANGER R.Study of parameters affecting the impact performance of an alloy wheel and noble approach followed to improve the impact performance[C].SAE Paper 2015-01-1514.
[22] 王宁,杜林秀,吴迪,等.超级钢汽车车轮强度有限元分析[J].东北大学学报(自然科学版),2006,27(7):779-781.
[23] 畅世为,张维刚.复合材料车轮冲击试验仿真分析[J].汽车工程,2010,32(1):65-68.
[24] SAH S K,BAWASE M A,SARAFM R.Light-weightmaterials and their automotive applications[C].SAE Paper 2014-28-0025.[25] BALLO F,MASTINUG,GOBBIM.Lightweight design of a racingmotorcycle wheel[C].SAE Paper 2016-01-1576.
[26] ROZVANY G IN.On symmetry and non-uniqueness in exact topology optimization[J].Structural and Multidisciplinary Optimization,2011,43(3):297-317.
[27] STEARNS J, SRIVATSAN T S, PRAKASH A, et al.Modeling themechanical response of an aluminum alloy automotive rim[J].Materials Science and Engineering: A,2004,366(2):262-268.
[28] COLLETM,BRUGGIM,DUYSINX P.Topology optimization for minimum weight with compliance and simplified nominal stress constraints for fatigue resistance[J].Structural and Multidisciplinary Optimization,2016:1-17.
[29] BRUGGIM,DUYSINX P.Topology optimization for minimum weightwith compliance and stress constraints[J].Structural and Multidisciplinary Optimization,2012,46(3):369-384.
[30] YIG,KIM N H.Identifying boundaries of topology optimization results using basic parametric features[J].Structural and Multidisciplinary Optimization,2016:1-14.
[31] HAHN Y,COFER J I.Study of parametric and non-parametric optimization of a rotor-bearing system[C].ASME Turbo Expo 2014:Turbine Technical Conference and Exposition.American Society of Mechanical Engineers, 2014: V07AT28A001-V07AT28A001.
[32] LEIFSSON L,HERMANNSSON E,KOZIEL S.Optimal shape design of multi-element trawl-doors using local surrogate models[J].Journal of Computational Science,2015,10:55-62.
[33] GOLZARIA,SEFATM H,JAMSHIDIS.Development of an adaptive surrogatemodel for production optimization[J].Journal of Petroleum Science and Engineering,2015,133:677-688.
[34] PAN I,DASS.Kriging based surrogatemodeling for fractionalorder control ofmicrogrids[J].IEEE Transactions on Smart Grid,2015,6(1):36-44.
[35] MEHMANIA,CHOWDHURY S,MESSACA.Predictive quantification of surrogatemodel fidelity based onmodal variations with sample density[J].Structural and Multidisciplinary Optimization,2015,52(2):353-373.
