采用极限学习机实现锂离子电池健康状态在线估算∗
2018-01-15潘海鸿吕治强韦海燕
潘海鸿,吕治强,付 兵,韦海燕,陈 琳
(1.广西大学机械工程学院,南宁 530000; 2.广西制造系统与先进制造技术重点实验室(广西大学机械工程学院),南宁 530000)
前言
锂离子电池因其能量密度大、循环寿命长、自放电率低和环保无污染等优点广泛应用于电动汽车领域[1-2]。为保证汽车电池工作可靠性,电池管理系统(battery management system,BMS)必不可少[3]。电池健康状态(state of health,SOH)决定电池更换时间和预测行驶里程,SOH在线估算也是BMS核心功能之一[4]。因此,准确估算锂离子电池SOH,对有效保障整车性能、电池利用最大化和避免电池意外失效等方面具有重要意义[5]。
锂离子电池SOH估算通常要求[6]:(1)计算简单;(2)精度高;(3)成本低且易于实施。因此,针对锂离子电池SOH在线估算,国内外展开大量探索性研究,主要方法可分为3类[7]:(1)直接测量法;(2)基于模型法;(3)数据驱动法。其中,直接测量法是基于SOH定义,通过专门设备测量电池当前最大可用容量或阻抗来计算SOH;直接测量法计算结果相对准确,但该方法耗时长且需要专门测量设备,难以在线实施[7]。基于模型法是建立电池等效模型,常用模型包括电化学模型[8]和等效电路模型[9]等,通过模型参数估算电池容量或阻抗进而估算电池SOH[8];该方法可在线实施,但其有效性和适应性受限于电池模型可信度和鲁棒性[10]。数据驱动法将电池视为“黑箱”,无须了解电池内部机理,通过智能算法,包括人工神经网络、支持向量机和模糊逻辑等,处理大量电池工作数据来估算电池SOH[7],具有较高灵活性和估算精度;但该方法计算量大,难以在线实施[11]。
文献[12]和文献[13]中首次提出具有精度高、速度快、参数简单等优点的极限学习机(extreme learningmachine,ELM)。ELM比BP神经网络、支持向量机(support vectormachine,SVM)和支持向量回归(support vector regression,SVR)等精度更高,耗时更短,已应用于其他领域。因此,基于锂离子电池Thevenin模型,将ELM引入电池SOH在线估算,提出一种模型和数据驱动融合方法。首先以锂离子电池在线辨识平均欧姆内阻增加量为表征电池衰退状态的健康指标(health indicator,HI);其次离线训练锂离子电池全生命周期衰减的ELM模型;最后基于动态工况在线辨识欧姆内阻,构建健康指标,并基于该健康指标和电池ELM衰退模型在线估算电池SOH。
1 基本方法
锂离子电池SOH表征电池存储电量能力,是定量描述电池衰退程度的指标,其计算公式为

式中:Qi为老化试验第i次循环后的电池最大可用容量;Q1为初始电池最大可用容量。
1.1 HI的构建
锂离子电池衰退状态识别是不同性能变量映射到对应HI以确定电池当前健康水平[4]。而从电池整个老化周期看,锂离子电池性能衰退的主要原因是随着锂离子电池充放电次数增加,固态电解质膜(solid electrolyte interphase,SEI)的扩展使得活性物质与电解液损耗[14],最终导致锂离子电池容量衰减和欧姆内阻增加。而在实际应用中,容量难以在线测量,只能通过在线可测量参数实现电池衰退识别。因此,提出在动态工况下辨识电池欧姆内阻,以平均欧姆内阻增加量构建表征电池衰退的HI。
构建HI,以表征电池衰退状态的详细过程如下。
以锂离子电池第一次容量测试作为基准,计算锂离子电池老化过程中的容量衰减量:

式中:ΔQi为第i次老化循环后电池容量衰减量,即容量退化状态。
从文献[15]和文献[16]中可以看出,锂离子电池欧姆内阻在[40%,90%]的荷电状态(state-ofcharge,SOC)区间内基本保持不变,且此区间也是电动汽车实际中SOC常用区间。因此,基于电池Thevenin模型,在线辨识电池欧姆内阻,根据式(3)计算SOC区间为[40%,90%]时的欧姆内阻平均值作为当前SOH的估算欧姆内阻,并记录第一次的平均欧姆内阻为R1。
式中:Ri为第i次老化循环后电池平均欧姆内阻;RSOC为动态工况下某一SOC时刻电池欧姆内阻;n为指定区间内的SOC数值个数。
以锂离子电池第一次平均欧姆内阻R1作为基准,根据式(4)分别计算锂离子电池老化过程中欧姆内阻增加量:

式中ΔRi为第i次老化循环后电池平均欧姆内阻增加量,即为构建的HI。
1.2 ELM基本原理
ELM是一种单隐层前馈神经网络[12-13],主要特点是将输入权值和隐节点偏差随机赋值,其网络结构如图1所示。

图1 ELM网络结构图
在图1中,{X}是输入训练数据集;{y}是对应输出测试数据集;{ω}是连接输入节点和隐节点的输入权值;{b}是隐节点偏差;{β}是连接隐节点和输出节点的输出权值;ELM包含L个隐节点,且一般隐节点数目小于输入训练数据集数目N。因此,当激活函数为g(x)时,建立ELM数学模型:

式中ωi·xj为ωi与xj的内积。
将式(5)改写为一个包含 L个方程的线性方程:

式中:β=[β1,β2,…,βL]T;y=[y1,y2,…,yN]T;H 为ELM隐含层输出矩阵,如式(7)所示:
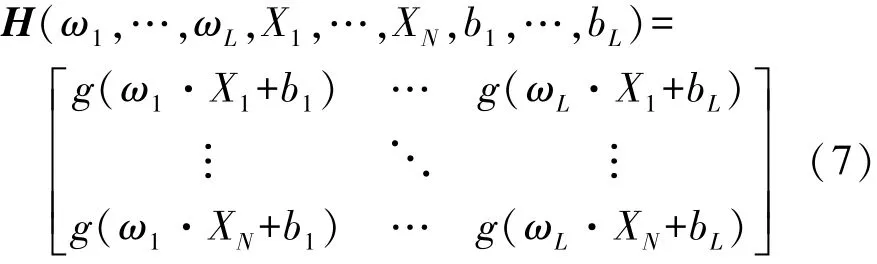
当激活函数无限可微时,对任意ωi和bi存在βi,使得式(8)成立[12-13]。

式中:H+为H的Moore-Penrose广义逆矩阵。
至此,求解出输出权值β即完成ELM训练。
2 ELM估算SOH方法
采用ELM实现锂离子电池SOH在线估算的方法,基本框架如图2所示,包括以下步骤。

图2 估算SOH方法框架
(1)ELM离线训练 首先,将电池进行小倍率电流放电,获取电池每次老化循环后的最大可用容量Qi;其次,将电池进行动态工况放电,实时采集电池工作电压电流,基于电池等效电路模型辨识电池欧姆内阻R;最后,计算NO.30电池全生命周期内的欧姆内阻增加量ΔR序列和容量衰减量ΔQ序列,以欧姆内阻增加量ΔR序列作为ELM输入训练数据集,容量衰减量ΔQ序列作为输出测试数据集,由式(5)~式(8)求解输出权值β,完成锂离子电池全生命周期衰减的ELM模型训练。
(2)HI在线构建 基于动态工况在线辨识目标电池(NO.17电池)欧姆内阻,计算欧姆内阻增加量ΔR,构建表征锂离子电池衰退的HI。
(3)SOH在线估算 将目标电池在线构建的HI,输入步骤(1)中已训练的电池ELM衰退模型,由式(5)实时在线计算目标电池容量衰减量估算值ΔQ^,再计算电池当前最大可用容量估算值Q,完成锂离子电池SOH在线估算。
3 实验设计
3.1 实验平台
该实验平台由锂离子电池、充放电系统和恒温箱等3部分组成。充放电系统由直流电源、电子负载仪和中央控制电脑组成,用于电池充电和模拟动态工况放电,并实时记录电池工作电压、电流和电量。温控系统主要部分是恒温箱,用于控制电池工作环境温度。
从同类型相同批次的三星三元锂离子电池ICR18650-26F中随机挑选两颗电池进行老化实验,编号分别为NO.30和NO.17,其详细参数见表1。

表1 三星ICR18650-26F电池参数
3.2 锂离子电池老化实验
为验证HI构建方法和引入的ELM方法在线估算电池SOH的有效性,进行锂离子电池全生命周期的老化验证实验。
依据电池使用手册,设计了锂离子电池老化实验流程,如图3所示。它包括电池容量测试、内阻测试和电池老化测试等3部分。
电池容量测试是为获取电池最大可用容量真实值,先将电池以标准 CC-CV(constont-current and constant-voltage)充电法满充后静置1h,再将电池进行小倍率电流放电至电池截止电压,记录电池初始最大可用容量为Q1,第i次老化循环后电池最大可用容量为Qi。在线内阻测试是先将电池以标准CCCV充电法满充后静置1h后,将电池统一以NEDC(new european driving cycle)动态工况循环放电至截止电压,电流如图4(a)所示,并利用Thevenin模型和递推最小二乘法在线辨识电池欧姆内阻。电池老化测试则是将电池以标准CC-CV充电法满充后静置1h后,将电池进行10次充放电循环,持续进行直至容量衰减20%,即当Qi/Q0≤80%,则认为该电池报废,停止实验[17]。其中,电池老化测试的放电部分,根据图3分别对2颗锂离子电池(NO.30和NO.17)采用不同的规范。
老化测试放电规范一:对NO.30锂离子电池老化测试的放电由60s,1.95A和15s,5.2A恒流放电组成,间隔15s(静置)后重复,如图4(b)所示,且将整个实验温度控制在35℃。
老化测试放电规范二:为加速锂离子电池老化速率,将NO.17电池老化实验循环实验温度提高到45℃。老化放电电流由 UDDS(urban dynamometer driving schedule)工况,30s,2.6A 和 120s,5.2A 恒流放电组成,如图4(c)所示。

图3 老化实验流程图

图4 不同工况下老化测试放电电流
4 结果分析
为评判以平均欧姆内阻增加量构建HI表征电池衰退状态和ELM估算电池SOH方法的准确性,首先验证欧姆内阻在线辨识精度;其次进行HI和容量衰减量的关联分析,验证HI的有效性;最后进行ELM在线估算电池SOH精度和鲁棒性验证。
4.1 电池模型参数在线辨识
在给定环境温度下,锂离子电池可视为受不同电池激励而产生相应端电压响应的单输入单输出系统。将与实测相同的激励电流输入电池Thevenin模型,基于递推最小二乘法实时辨识模型参数。若算法充分收敛后,模型估算端电压与实测电池端电压误差不超过一定阈值(电池放电截止电压的1%),则认为电池模型足够精确[18]。此外,根据文献[16]可知,与高温相比,低温时电池欧姆内阻对温度的变化更加敏感,变化速率更大,这是由电解质溶液中的离子移动速度决定的。因此,本方法适用于锂离子电池工作的温度范围为25~40℃之间。
随机挑选NO.30电池老化实验中欧姆内阻测试部分的一次NEDC工况进行电池模型参数辨识,结果如图5所示。

图5 电池模型参数在线辨识结果
由图5(a)和图5(b)可见,电池实测端电压曲线和模型估算端电压曲线具有较高重合度,两者之间的整体估算误差小于±5mV,小于电池截止电压的1%(27.5mV)。表明电池Thevenin模型能真实模拟锂离子电池的动态特性,且递推最小二乘法能实现锂离子电池模型参数准确估算。由图5(c)可见,当SOC低于0.2时,欧姆内阻变化较为剧烈;而在[40%,90%]的SOC区间内基本保持不变。因此,以此区间内欧姆内阻平均值作为当前健康状态下的估算欧姆内阻可有效避免个别异常值的影响,保证HI的鲁棒性。
4.2 关联分析
为验证以平均内阻增加量构建HI的有效性,展开HI与容量衰减量的关联分析,定量判定锂离子电池平均欧姆内阻增加量对容量衰减量的影响程度。
将NO.30和NO.17电池容量衰减量和HI数据经低通滤波器处理后,利用式(9)分别计算Pearson相关系数rp和Spearman相关系数rs,进行关联度分析,结果如表2所示。
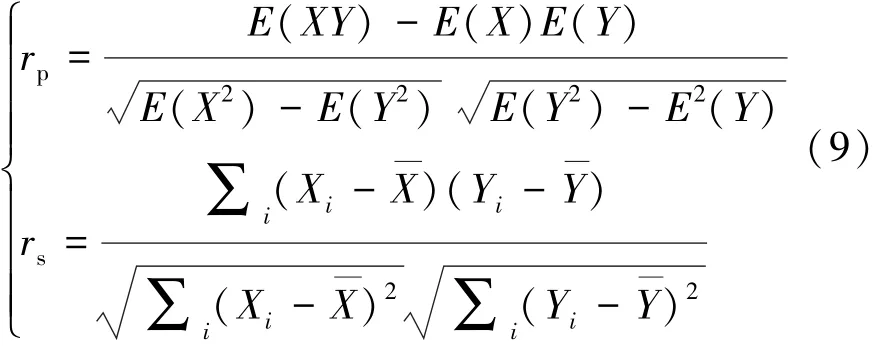
式中:X,Y分别为待求解关联系数的两个数据序列。

表2 相关系数统计表
在实际应用中,以X代表构建的健康指标ΔR序列,Y代表电池容量衰减量ΔQ序列。
rp是定量描述两个数据序列之间线性关系的评价标准,rs是度量两个变量之间是否严格单调的指标[19]。rp和rs越接近于1,则说明两组数据之间近似线性关系越明显。
从表2可知,NO.30电池和NO.17电池的两种相关系数(rp和rs)计算结果都接近于1,表明锂离子电池老化过程中平均欧姆内阻增加量ΔR和容量衰减量ΔQ之间存在强相关关系。因此,以在线获取平均欧姆内阻增加量ΔR构建锂离子HI描述锂离子电池性能衰退状态,进而基于两者之间的近似线性关系训练的电池ELM衰退模型估算锂离子电池SOH理论上是可行的。
4.3 容量衰减在线估算
在实现在线估算前,必须离线建立ELM的模型,然后以NO.30电池提供的历史数据离线训练电池ELM衰退模型,再以NO.17电池作为目标电池,基于建立的ELM模型实现SOH在线估算,并验证该方法精度,具体步骤如下。
首先,利用NO.30电池全生命周期的历史测试数据(容量测试数据和欧姆内阻测试数据),以平均欧姆内阻增加量构建与电池衰退状态相一致的HI。设置隐节点个数为20,激活函数类型为Sigmoid函数,离线训练电池全生命周期ELM衰退模型,建立HI与电池容量衰减状态的定量关系。
其次,通过动态工况在线辨识NO.17电池欧姆内阻,构建HI,输入已训练完成的ELM衰退模型中进行容量衰减在线估算。
最后,根据容量衰减估算值计算电池当前最大可用容量,完成SOH在线估算。
基于上述流程,使用 ELM方法在线计算出NO.17锂离子电池容量衰减量估算值ΔQ^,结果如图6所示。

图6 在线估算容量衰减结果
由图6(a)可见,在锂离子电池老化过程中,欧姆内阻不断增加,容量不断衰减。而容量衰减量与电池平均欧姆内阻增加量近似成线性关系[4]。基于此关系训练电池容量衰减的ELM模型,能准确跟踪电池容量衰减变化,容量衰减量最大估算误差不超过0.04A·h(图6(b)),即不超过电池额定容量的2%。
为详细说明基于ELM所建电池衰退模型的优劣,将模型的训练时间,估算值和真实值的均方根误

式中:ΔQ为NO.17电池实测容量衰减真实值;ΔQ^为采用ELM模型计算的电池容量衰减估算值。
根据式(10)分别计算ELM估算模型训练数据精度(RMSE)为0.014,测试数据精度为0.017,记录训练时间0.010s。从精度和时间两方面可以看出,ELM整体估算电池容量衰减性能较好,且运行时间较短,充分体现了ELM速度快、精度高的优点。
4.4 SOH在线估算
将式(2)变形得式(11),根据4.3节中NO.17电池初始电池最大可用容量Q1和采用ELM方法在线估算的容量衰减量,可由式(11)计算出电池最大可用容量估计值,结果如图7所示。


图7 最大可用容量计算结果与真实值的对比
由图7可见,随着电池不断老化,其容量随着平均欧姆内阻的增加而不断降低。而电池容量各点之间间距不同,间接说明电池老化是一个复杂的非线性时变过程。
根据式(11)估算的电池最大可用容量Q^和老化实验二中获取的电池实测最大可用容量Q,由式(1)分别计算出锂离子电池SOH在线估算值和SOH真实值,对比结果如图8所示。
由图8可见,随着电池逐渐老化过程,锂离子电池容量不断下降,使用ELM在线估算的电池SOH曲线能很好地与真实SOH曲线重合。SOH估算误差也随着电池老化上下波动,最大不超过2%。差作为评价指标来评价模型。其中均方根误差(root-mean-square error,RMSE)主要衡量估算值同真实值之间的偏差,RMSE越接近于0说明估算值越接近于真实值,其定义为

图8 在线估算SOH结果
分别计算SOH估算值的最大估算误差(maximum error, ME),平均绝对误差(mean absolute error,MAE)和RMSE,以衡量SOH在线估算精度,结果如表3所示。

表3 SOH在线估算结果评价
从表3可知,SOH估算值与SOH真实值之间RMSE为0.005 9,且整体估算误差不超过2%,估算精度较高。一方面是在线构建的健康指标能准确反映电池衰退状态;另一方面,ELM学习速度快,泛化精度高,不会陷入局部最小值,且有多种无限可微的激活函数选择[12-13],有利于锂离子电池SOH的在线估算。
5 结论
针对电动汽车锂离子电池SOH在线估算问题,引入ELM方法,并进行三元锂离子电池老化实验验证,得到如下结论。
(1)在动态工况下,以欧姆内阻增加量ΔR构建表征锂离子电池衰退状态的健康指标HI,并通过Pearson和Spearman相关系数证明HI的有效性。
(2)基于锂离子电池全生命周期的HI和容量衰减量ΔQ,采用ELM方法离线训练锂离子电池容量衰减模型。结果表明,该模型能准确描述电池衰退状态。
(3)在线构建电池健康指标HI,应用电池全生命周期的ELM衰退模型实现SOH在线估算。结果表明,SOH在线估算耗时较短,且估算误差不超过2%。
[1] 李军求,吴朴恩,张承宁.电动汽车动力电池热管理技术的研究与实现[J].汽车工程,2016,38(1):22-27.
[2] 王常虹,董汉成,凌明祥,等.车用锂离子电池剩余使用寿命预测方法[J].汽车工程,2015,37(4):476-479.
[3] 毕军,康燕琼,邵赛.纯电动汽车动力锂电池Nernst模型参数辨识[J].汽车工程,2015,37(6):725-730.
[4] 董汉成,凌明祥,王常虹,等.锂离子电池健康状态估计与剩余寿命预测[J].北京理工大学学报,2015,35(10):1074-1078.
[5] OZKURT C,CAMCI F,ATAMURADOV V,et al.Integration of sampling based battery state of health estimation method in electric vehicles[J].Applied Energy,2016,175:356-367.
[6] TORAIS,NAKAGOMIM,YOSHITAKE S,et al.State-of-health estimation of LiFePO4/graphite batteries based on a model using differential capacity[J].Journal of Power Sources,2016,306:62-69.
[7] BERECIBAR M, GANDIAGA I, VILLARREAL I, et al.Critical review of state of health estimation methods of Li-ion batteries for real applications[J].Renewable and Sustainable Energy Reviews,2016,56:572-587.
[8] BARTLETT A, MARCICKI J, ONORI S, et al.Electrochemical model-based state of charge and capacity estimation for a composite electrode Lithium-Ion battery[J].IEEE Transactions on Control Systems Technology,2016,24(2):384-399.
[9] DAIH F,WEIX Z,SUN ZC.A new SOH prediction concept for the power lithium-ion battery used on HEVs[C].IEEE Vehicle Power and Propulsion Conference VPPC.NEW YORK: IEEE,2009:1432-1436.
[10] HU X,JIANG J,CAOD,etal.Battery health prognosis for electric vehicles using sample entropy and sparse bayesian predictive modeling[J].IEEE Transactions on Industrial Electronics,2016,63(4):2645-2656.
[11] CHEN L,LINW,LI J,et al.Prediction of lithium-ion battery capacity with metabolic greymodel[J].Energy,2016,106:662-672.
[12] HUANG G,ZHUQ,SIEW C.Extreme learningmachine:Theory and applications[J].Neurocomputing,2006,70(1-3):489-501.
[13] ZHANG K,LUO M.Outlier-robust extreme learningmachine for regression problems[J].Neurocomputing,2015,151(3):1519-1527.
[14] 董汉成.卫星电源电池健康状态诊断方法研究[D].哈尔滨:哈尔滨工业大学,2015.
[15] XIONG R,HE H,SUN F,et al.Evaluation on state of charge estimation of batteries with adaptive extended kalman filter by experiment approach[J].IEEE Transactions on Vehicular Technology,2013,62(1):108-117.
[16] 李哲.纯电动汽车磷酸铁锂电池性能研究[D].北京:清华大学,2011.
[17] 陈琳,田彬彬,林伟龙,等.影响锂离子电池SOC因素的灰色关联分析[J].电测与仪表,2016,53(13):5-9.
[18] 熊瑞.基于数据模型融合的电动车辆动力电池组状态估计研究[D].北京:北京理工大学,2014.
[19] 周建宝.基于RVM的锂离子电池剩余寿命预测方法研究[D].哈尔滨:哈尔滨工业大学,2013.
