新超混沌系统的线性反馈修正投影同步的电路实现

李德奎

(甘肃中医药大学，理科教学部，甘肃 定西743000)

新超混沌系统的线性反馈修正投影同步的电路实现

李德奎

(甘肃中医药大学，理科教学部，甘肃 定西743000)

研究了新超混沌系统的线性反馈修正投影同步及电路实现．首先对Lorenz系统反馈控制并应用Lyapunov指数方法，提出一个新超混沌系统，然后基于Lyapunov稳定性定理，利用最简单的线性反馈控制，实现该新超混沌系统的修正投影同步，最后通过数值仿真验证理论分析的正确性，并构建新超混沌系统修正投影同步的仿真电路，示波器显示出的修正投影同步波形图与数值仿真的结果一致，说明该新超混沌系统修正投影同步电路实现的可行性及正确性．

线性反馈； 修正投影同步； 电路实现； 新超混沌系统

构造和研究混沌系统模型是混沌应用的基础，1963年，气象学家Lorenz提出了著名的Lorenz混沌系统[1]，该系统的提出开启了混沌研究和应用的新纪元．随后许多混沌和超混沌系统模型被先后提出[2-8]．Lyapunov指数是衡量系统动力学特性的一个重要定量指标，表示了系统在相空间中相邻轨道间收敛或发散的平均指数率.正的Lyapunov指数表示在系统相空间中，无论初始2条轨线的间距多么小，其差别都会随着时间的演化而成指数率的增加，达到无法预测的混沌现象.正的Lyapunov指数越多，表明系统的混沌特性越强，具有1个正的Lyapunov指数值的系统称为混沌系统，具有2个或2个以上正的Lyapunov指数值的系统称为超混沌系统，超混沌系统模型的构造是混沌研究的一个热点.文献[9]提出了一个新超混沌系统，研究了系统发生Hopf分岔的参数条件，并构建了新超混沌系统的仿真电路，得到了与数值仿真相同的混沌吸引子.

1990年，Pecora 和Carroll提出了驱动-响应混沌同步策略[10]．随后耦合控制策略[11-12]、反馈控制策略[4,13]、自适应控制策略[14]等．通过自适应控制器的作用，2个混沌系统不需要人为干预，随着时间的变化就能够实现同步，但是自适应控制器结构比较复杂，电路实现比较困难.反馈控制法分为线性反馈同步[4, 13-15]和非线性反馈同步[16-17]方法，其中非线性反馈同步同样有电路实现比较困难的缺陷，线性反馈同步电路实现较为方便.

近年来，许多混沌同步方法先后被学者提出，例如完全同步[18]、相同步[19]、滞后同步[20]、广义同步[21]和投影同步[22-23]．投影同步是指驱动系统与响应系统的状态变量之间以不等于1的常数比例实现同步.相比较以上各种同步方法，投影同步能够使得混沌通信更加安全可靠，所以投影同步近年来得到广泛的研究[24-25]．

修正投影同步是指驱动系统和响应系统的各对状态变量以不同的比例因子实现同步，因此，在混沌遮掩保密通信中，攻击者即使得到信道中的传输信号和遮掩有用信号的混沌系统，由于不知道其同步比例因子，就很难准确将有用信号重新还原，提高了保密通信的安全性[26]．

基于以上考虑，笔者利用Lyapunov稳定性定理和牵制控制方法，设计同步线性反馈控制器.在控制器作用下实现新超混沌系统[9]的修正投影同步，然后进行数值仿真验证同步控制器的有效性，最后利用Multisim电路仿真平台构建新超混沌系统修正投影同步的仿真电路，为新超混沌系统修正投影同步在保密通信中应用奠定电路基础.

1 线性反馈修正投影同步

新超混沌系统[9]的微分方程组为

(1)

当参数a=10,b=28,c=2,θ=4，k=8时，系统(1)处于超混沌状态，且有如图1所示的混沌吸引子．

图1 新超混沌系统的奇怪吸引子

线性反馈控制结构形式简单，电路实现容易，在实际应用中具有更大普适性，针对超混沌系统(1)构造响应系统为

(2)

其中，[y1,y2,y3,y4]为响应系统的状态向量，[k1,k2,k3,k4]线性反馈系数向量，[α1,α2,α3,α4]为修正投影同步的比例因子向量．

设误差e1=y1-α1x1，e2=y2-α2x2,e3=y3-α3x3,e4=y4-α4x4,且设同步比例因子α1=α2=α4，于是得到驱动系统(1)和响应系统(2)的误差系统为

(3)

当修正投影同步的比例因子满足α2=α1α3，α3=α1α2时，误差系统(3)重写为

(4)

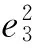
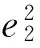
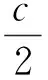
(5)

当系统(1)和(2)同步时，比例因子满足

(6)

此方程组有2组解α3=1,α1=α2=α4=-1和α1=α2=α2=α4=1．

取系统(1)和(2)实现同步的比例因子为α3=1，α1=α2=α4=-1，系统(1)和(2)实现修正投影同步.

2 数值仿真

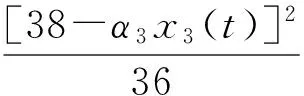
根据(5)式并结合图2，取线性反馈系数，k1=40，k2=10，k3=20,k4=18．取初值为[x1,x2,x3,x4]=[0.1，-1，2，-0.3]，[y1,y2,y3,y4]=[1,0,1,-1]，采用步长为0.01的四阶龙格库塔方法进行仿真，得到系统(1)和(2)的同步状态误差曲线，如图3所示．

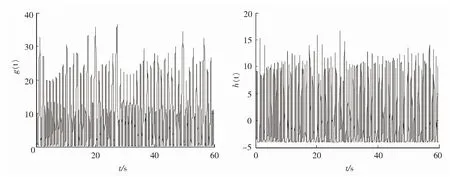
图2 函数g(t)和h(t)的时间序列图

由图3可以看出，通过线性反馈控制，系统(1)和(2)能够在不到0.5s的时间里实现修正函数投影同步，同步时间非常快．

图3 系统(1)和(1)的同步状态误差曲线图

图4中实线表示系统(1)的状态曲线，虚线表示系统(2)的状态曲线．从图4所示的系统(1)和(2)的状态同步时间序列图可以看出，系统(1)的状态变量x1，x2，x4和系统(2)的状态变量y1，y2，y4按比例因子-1实现反相位同步，而系统(1)的状态变量x3和系统(2)的状态变量y3按比例因子1实现完全同步．在2个系统之间的各状态变量按照不同的比例因子实现同步，从而验证了系统(1)和(2)之间通过线性反馈控制，能够实现修正投影同步．

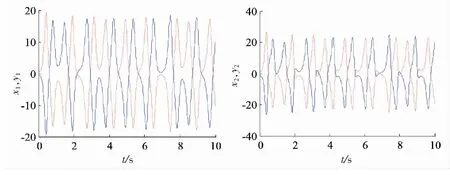
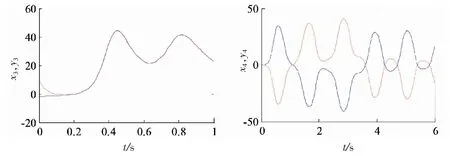
图4 系统(1)和(2)的同步状态时间序列图

3 同步电路设计

基于非线性电路设计原理，基于同相比例器、反相比例器、乘法器和积分运算器等，设计驱动系统(1)和响应系统(2)的修正投影步电路(如图5所示)，其中虚线框里面的电路实现了驱动系统(1)，电路中所有的运算放大器型号均为TL084CN，乘法器型号为AD633(增益为0.1),所有的电容器的电容为1μF，其余电路元件参数值如图5所示．

虚线框内的电路仿真驱动系统(1)，用电压u1,u2,u3,u4分别实现驱动系统⑴的状态变量x1,x2,x3,x4．虚线框外的电路仿真响应系统(2)，用电压v1,v2,v3,v4分别实现响应(2)的状态变量y1,y2,y3,y4．设计新超混沌系统线性反馈修正投影同步的仿真电路如图5所示．

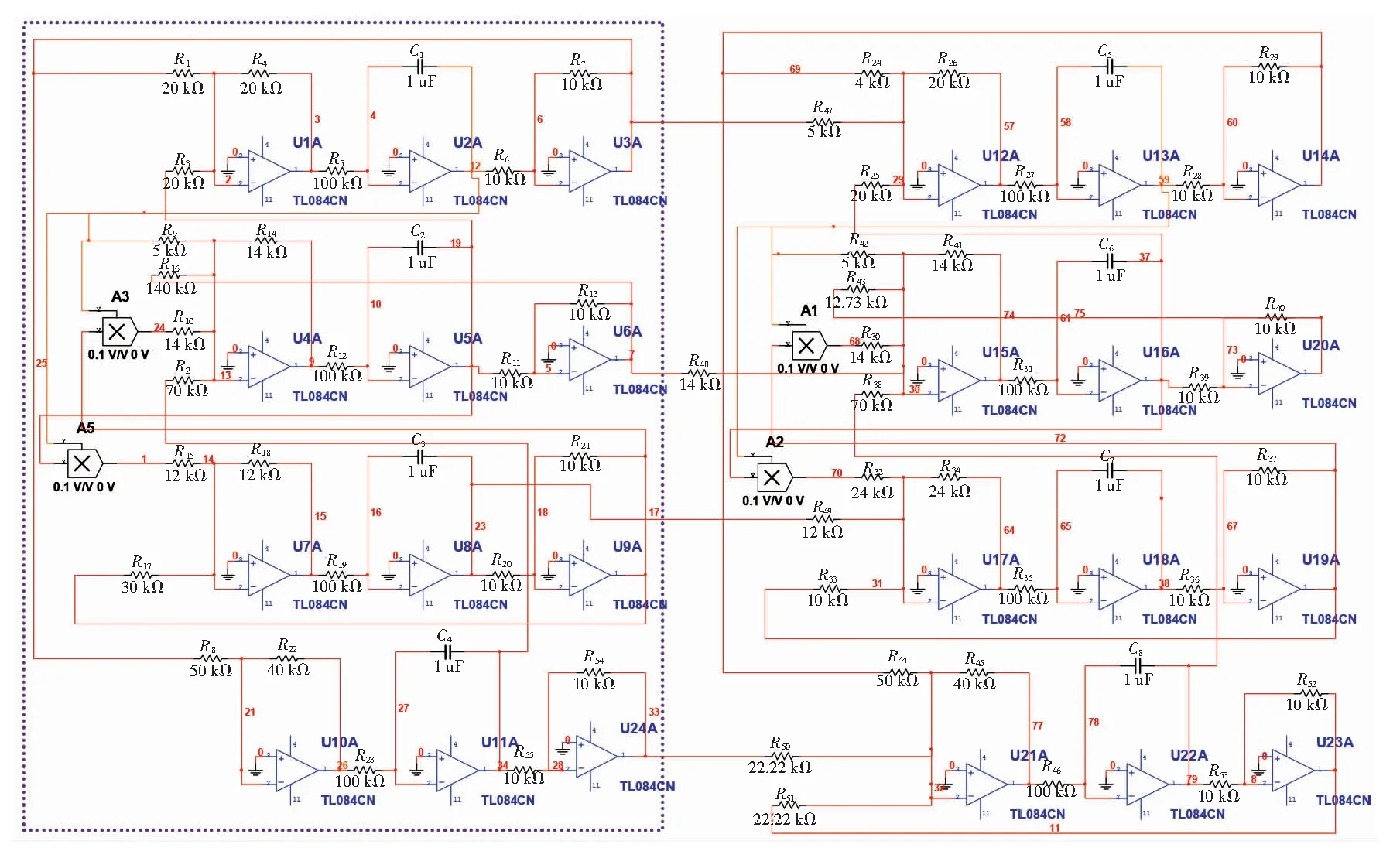
图5 系统(1)和(2)的修正投影同步电路图

根据图5所示的驱动系统(1)和响应系统(2)的修正投影同步电路图，并结合电路理论知识，可以得图5的电路状态方程为

图5所示模拟电路的示波器显示出修正投影同步的电压波形如图6所示．示波器1、2、4上分别显示出u1和v1,u2和v2,u4和v4按比例因子-1实现反同步，而示波器3上显示出u3和v3按比例因子1实现完全同步．图6所示的驱动响应系统同步波形图,与Matlab仿真得到的图4所示的同步波形图一致，说明新超混沌系统线性反馈修正投影同步电路实现是可行的．

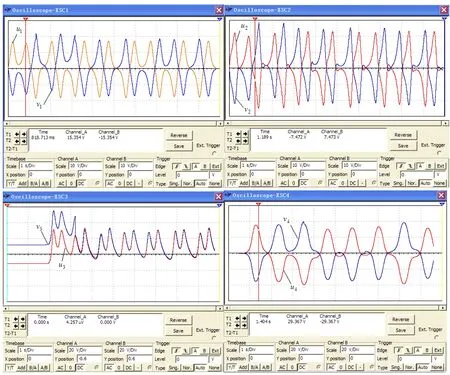
图6 示波器显示同步波形图

4 小 结

通过研究新超混沌系统的线性反馈修正投影同步及其电路仿真，得出以下结论

1) 理论分析和数值仿真的结果表明，所构造的线性反馈控制器能够实现新超混沌系统的修正投影同步，该线性反馈控制器具有有效性.

2) 构建实现新超混沌系统修正投影同步的仿真电路，示波器显示出的修正投影同步波形图与数值仿真的波形图一致，说明电路实现新超混沌系统修正投影同步的可行性和电路设计的正确性．

[1] Lorenz E N. Deterministic non-periodic flow[J]. Journal of Atmosphere Science, 1963, 20: 130-141.

[2] Chen G R, Ueta T. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos，1999, 9(7): 1 465-1 466.

[3] Suwat K. Chaos synchronization of unified chaotic systems via LMI[J]. Physics Letters A . 2009, 373(32): 2 837-2 840.

[4] 陶朝海，陆君安，吕金虎．统一混沌系统的反馈同步[J]. 物理学报，2002, 51(7):1 497-1 501．

[5] Xu Y H,Lu Y J,Xie C R,et al. Impulsive synchronization of Lü chaotic systems via the hybrid controller[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(5): 2 575-2 578.

[6] Xue W,Fang Y F,Li Q. A novel four-wing hyper-chaotic system and its circuit implementation[J]. Procedia Engineering, 2012, 29: 1 264-1 269.

[7] Niu Y J, Wang X Y, Wang M J,et al. A new hyperchaotic system and its circuit implementation [J]. Communications in Nonlinear Science and Numerical Simulation , 2010, 15(11):3 518- 3 524.

[8] Qia G Y,Van Wyk M A ,Van Wyk B J,et al. On a new hyperchaotic system[J]. Physics Letters A, 2008,372( 2): 124-136.

[9] 李德奎.一个新超混沌Lorenz系统的Hopf分岔及电路实现[J]. 宁夏大学学报:自然科学版，2016, 37(3): 294-300.

[10] Pecora L M, Carroll T L. Synchronization in chaotic system[J]. Physics Letters A, 1990, 64(4): 821-824.

[11] Jiang G P,Tang W K S, Chen G R. A simple global synchronization criterion for coupled chaotic systems [J]. Chaos, Solitons and Fractals, 2003, 15 (5): 925-935.

[12] Li D M,Lu J A, Wu X Q. Linearly coupled synchronization of the unified chaotic systems and the Lorenz systems [J]. Chaos, solitons & Fractals, 2005, 23(1): 79-85.

[13] 刘扬正，姜长生．线性反馈控制新的4维超混沌系统同步[J]. 四川大学学报:工程科学版, 2007, 39(6): 138-142.

[14] Rafikova M, Balthazarb J M.On control and synchronization in chaotic and hyperchaotic systems via linear feedback control [J]. Communications in Nonlinear Science and Numerical Simulation, 2008,13(7):1 246-1 255.

[15] Pan H,Nian X H,Gui W H. Synchronization in dynamic networks with time-varying delay coupling based on linear feedback controllers[J].Acta Automatica Sinica, 2010, 36(12): 1 766-1 798.

[16] 陈志盛, 孙克辉, 张泰山. Liu混沌系统的非线性反馈同步控制[J]. 物理学报, 2005, 54(6): 2 580-2 583.

[17]李德奎,连玉平,张建刚. 时变时滞耦合复杂网络的函数投影同步[J]. 北京工业大学学报, 2015,41(2): 207-214.

[18] Agiza H N . Chaos synchronization of Lü dynamical system [J]. Nonlinear Analysis, 2004, 58(1/2):11-20.

[19] Pikovsky A S, Rosenblum M G, Osipov G V. Phase synchronization of chaotic oscillators by external driving [J]. Physica D: Nonlinear Phenomena, 1997, 104(3/4):219-238.

[20] Li C D, Liao X F, Wong K W. Chaotic lag synchronization of coupled time-delayed systems and its applications in secure communication[J]. Physica D: Nonlinear Phenomena, 2004, 194(3/4):187-202.

[21] Rulkov N F, Sushchik M M, Tsimring L S, et al. Generalized synchronization of chaos in directionally coupled chaotic systems[J]. Phys. Rev.E, 1995,51: 980-994.

[22] Yan J P, Li C P. Generalized projective synchronization of a unified chaotic system [J]. Chaos Solitons and Fractals, 2005, 26(4):1 119-1 124.

[23] Agrawal S K, Das S. Function projective synchronization between four dimensional chaotic systems with uncertain parameters using modified adaptive control method [J]. Journal of Process Control, 2014, 24(5): 517-530.

[24] Li C P, Yan J P. Generalized projective synchronization of chaos: the cascade synchronization approach [J].Chaos Solitons and Fractals, 2006, 30(1):140-146.

[25] Li Z A, Xu D L. Stability criterion for projective synchronization in three-dimensional chaotic systems[J]. Physics Letters A, 2001, 282(3): 175-179.

[26] 方洁，姜长生．错位修正混沌函数投影同步及在保密通信中的应用[J]．四川大学学报：工程科学版,2011,43(2):137-149．

CircuitImplementationforLinearFeedbackModifiedProjectiveSynchronizationofANewHyper-chaoticSystem

Li Dekui

(Department Teaching of Science, Gansu University of Chinese Medicine, Dingxi 743000, China)

In the report, the linear feedback modified projective synchronization and circuit implementations were studied. At first, a new hyperchaotic system was put forward by a feedback control for Lorenz system; secondly, based on the Lyapunov stability theorem, the simplest linear feedback control was used to implement the modified projective synchronization of the new superchaotic system; finally, the numerical simulation experiments were performed to verify the correctness of the theoretical analysis, and the simulation circuit of a modified projective synchronization for the new hyperchaotic system was constructed. The results indicated that some modified projection synchronization waves from the oscilloscopes were consistent with the results of numerical simulation, which suggested that the circuit implementation of the modified projection synchronization for the new hyperchaotic system was feasible and correct.

linear feedback; modified projective synchronization; circuit implementation; a new hyper-chaotic system

2017-09-28

甘肃省自然科学基金(1610RJZA080)；甘肃省高等学校科研项目(2017A-155)

李德奎(1979-)，男，甘肃通渭人，副教授，硕士，研究方向：混沌理论及应用，E-mail: dkli2009@163.com

1004-1729(2017)04-0329-08

O 415.5

ADOl10.15886/j.cnki.hdxbzkb.2017.0051