耦合Schrödinger-KdV方程的高阶离散线积分方法

陈宵玮，孙建强

(海南大学 信息科学技术学院,海南 海口 570228)

耦合Schrödinger-KdV方程的高阶离散线积分方法

陈宵玮，孙建强

(海南大学 信息科学技术学院,海南 海口 570228)

基于四阶平均向量场方法和Boole离散线积分理论，提出了哈密尔顿系统的高阶Boole离散线积分方法.利用高阶Boole离散线积分方法求解具有能量守恒特性的耦合Schrödinger-KdV方程，得到了耦合Schrödinger-KdV方程的新的高阶格式.数值模拟结果表明新的高阶格式能很好地模拟耦合Schrödinger-KdV方程的演化行为，并能很好地保持方程的离散能量守恒.

耦合Schrödinger-KdV方程； 高阶离散线积分方法； 哈密尔顿系统

非线性现象在应用数学和物理研究中占有非常重要的作用.许多非线性现象需要通过耦合的偏微分方程来描述,如KdV-mKdV方程、KdV-ZK方程、Schrödinger-KdV方程等.特别是耦合Schrödinger-KdV方程在等离子体物理中的广泛应用，已成为研究的热点.讨论如下耦合Schrödinger-KdV方程[1]

(1)

(2)

其中,I(0)为常数.在理论上,已有许多关于耦合Schrödinger-KdV方程的研究，如耦合Schrödinger-KdV方程柯西问题适定性[2]和方程的精确解[3]等.在数值模拟中，张弘等人给出了耦合Schrödinger-KdV方程的二阶平均向量场方法，该方法能很好地模拟方程的行为，并精确地保持了微分方程的能量；Izady[4]等人提出了对于方程的傅里叶变换的一种分解方法；Golbabai[5]等人提出了对于该方程数值解的无网格方法.

在1996年Gonzalez[6]首次提出离散梯度方法后，McLachlan[7]等人在离散梯度法的基础上提出了平均向量场方法，并已广泛应用于偏微分方程的计算[8],取得了较好的数值结果.Iavernaro[9]等人利用离散线积分方法对二阶平均向量场方法的积分项数值离散得到了一个新的计算格式. 后来Quispel[10]和Celledoni[11]提出了高阶平均向量场方法.利用四阶平均向量场方法和Boole离散线积分理论得到了高阶Boole离散线积分方法并应用于耦合Schrödinger-KdV方程的计算.

1 高阶Boole离散线积分方法

考虑如下哈密尔顿系统

(3)

其中，H∶Rn→R是哈密尔顿函数，S是反对称矩阵，哈密尔顿系统具有能量守恒特性.

1999年Quispel等人提出了哈密尔顿系统(3)如下的二阶平均向量场方法

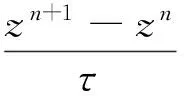
(4)

其中，τ是时间步长，并证明了该方法能够保持哈密尔顿系统(3)不同时刻的能量守恒，即满足

H(zn+1)=H(zn).

(5)

2007年Iavernaro等人在二阶平均向量场方法的基础上提出如下Boole离散线积分方法.

假设初值是zn，在t=τ处的数值解为zn+1，设连接zn和zn+1的最简单路径为

(6)

并对二阶平均向量场格式(4)右边的积分项进行Boole积分，令Zi=σ(c1)≡cizn+1+(1-ci)zn,可以得到如下的Boole离散线积分公式

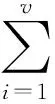
(7)

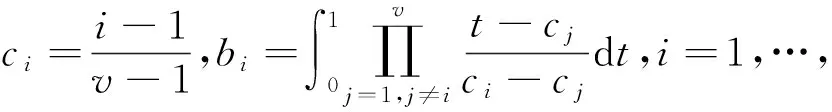
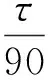
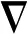
(8)

当多项式哈密尔顿函数H的次数小于等于4时，式(8)可以精确地保持哈密尔顿系统(3)的能量守恒.

2008年Quispel等人提出了保哈密顿系统能量守恒的高阶平均向量场方法

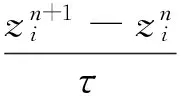
(9)

根据式(9),给出四阶平均向量场方法如下的矩阵向量形式

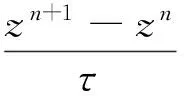
(10)

基于Boole离散线积分的理论，对四阶平均向量场方法(10)的积分项进行数值积分，得到如下的

高阶Boole离散线积分格式

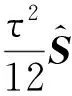
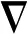
(11)

显然，格式(11)在时间方向上同样具有四阶精度.

2 耦合Schrödinger-KdV方程的高阶Boole离散线积分格式

设E(x,t)=p(x,t)+q(x,t)i，耦合Schrödinger-KdV方程等价于

(12)

方程(12)可以表示成典则哈密尔顿系统

(13)

其中,z=(p,N,q)T,∂x为一阶偏导数，相应的哈密尔顿函数为

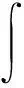
(14)

对系统(13)在空间方向上用拟谱方法离散[12-13].对于∂xxx用谱微分矩阵D1D2近似离散，从而可得到方程(1)的半离散拟谱格式

(15)

(16)

(17)

其中,di,j是矩阵D1第i行，第j列的元素,A=D1D2，而D1和D2分别是如下一阶谱矩阵和二阶谱矩阵

方程(15～17)在空间方向拟谱离散后可写成有限维哈密尔顿系统

(18)

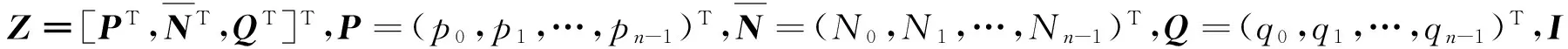
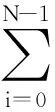
(19)

对格式(18)用四阶平均向量场方法进行离散，有

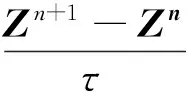
(20)

(21)

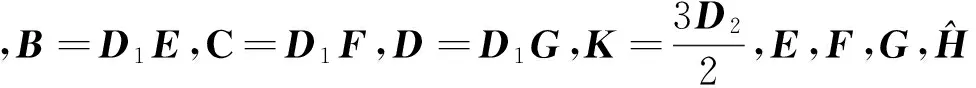
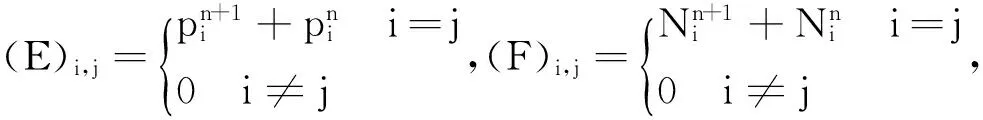
将耦合Schrödinger-KdV方程的四阶平均向量场格式(20)的积分项用Boole离散线积分离散，有

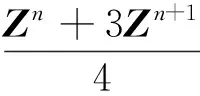
(22)

格式(22)表示成如下矩阵向量形式

(23)

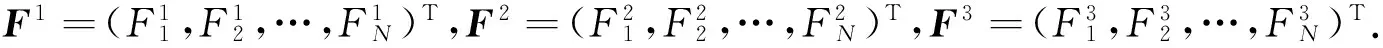
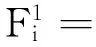
(24)

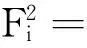
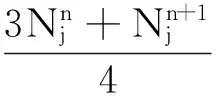
(25)

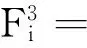
(26)

为了验证耦合Schrödinger-KdV方程新格式(23)的保能量守恒特性，定义能量误差为

(27)

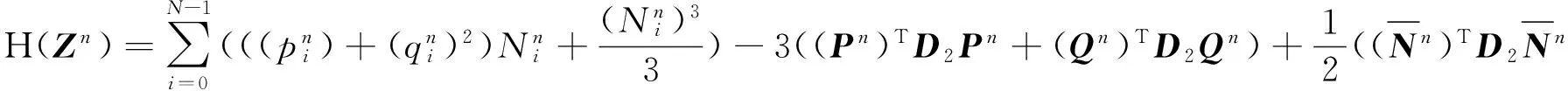
3 数值模拟

3.1 单孤立波的模拟 设方程(1)的初始条件为

(28)

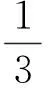
(29)

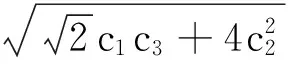
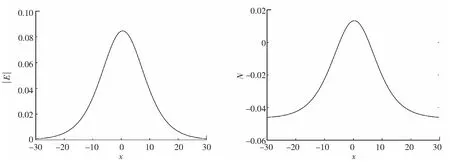
图1 |E|在t=1时刻的数值解 图2 N在t=1时刻的数值解

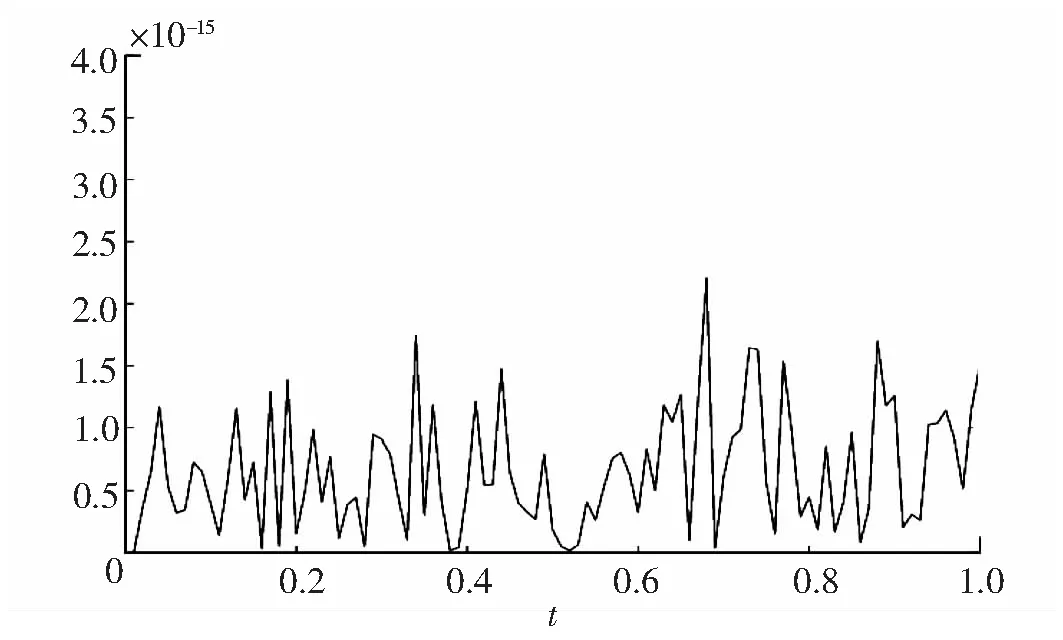
图3 数值解在t[0,1]内能量误差变化

由图1～2可知,格式(23)能够很好地模拟方程单孤立波的传播，数值结果与文献[1]一致.由图3可知，方程(1)在相应时间内的能量误差已达到10-15，能量误差可忽略不计.由图1～3可知，耦合Schrödinger-KdV方程高阶离散线积分格式(23)能很好地模拟方程孤立波的演化行为，且很好地保持了方程的离散能量.

3.2 多孤立波的演化情况 设方程(1)初始条件为

(30)

(31)

由图4～5可知,格式(23)能够很好地模拟方程多孤立波的传播.由图6可知，方程(1)在相应时间内的能量误差已达到10-13，故能量误差可忽略不计.由图4～6可知，耦合Schrödinger-KdV方程高阶离散线积分格式(23)同样能有效地模拟方程多孤立波的演化行为，并很好地保持了方程的离散能量.

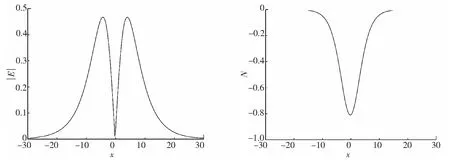
图4 |E|在t=1时刻的数值解 图5 N在t=1时刻的数值解

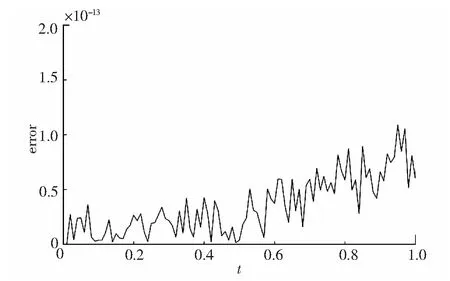
图6 数值解在t[0,1]内能量误差变化

4 小 结

在四阶平均向量场方法和Boole离散线积分理论的基础上，首先构造了耦合Schrödinger-KdV方程的新的高阶Boole离散线积分格式，其次在不同初值条件下对方程进行数值模拟并分析新格式的相对能量误差，最后计算结果表明得到的新格式既能较好地模拟耦合Schrödinger-KdV方程孤立波的行为，也能较好地保持方程的离散能量守恒.

[1] Zhang H , Song S H, Chen X D,et al. Average vector field methods for the coupled Schrödinger KdV equations[EB/OL].[2017-06-10]. https://www.researchgate.net/publication/263668796_Average_vector_field_methods_for_the_coupled_Schrodinger-KdV_equations.

[2] Guo B L, Miao C X. Well-Posedness of the Cauchy problem for the coupled system of the Schrödinger-KdV equations[J].Acta Mathematica Sinica, English series. 1999,15 (2): 215-224.

[3] 陈贺灵,孙福伟.耦合Schrödinger-KdV的精确解[J].北方工业大学学报, 2007, 19 (1): 54-65.

[4] Izady P, Zand A. A new algorithm for solving coupled Schrödinger KdV equation: an application of the Fourier transform adomian decomposition method[J]. Advanced Studies in Theoretical Physics, 2014, 8(8): 357-364.

[5] Golbabai A, Safdari-Vaighani A. A meshless method for numerical solution of the coupled Schrödinger-KdV equations[J]. Springer-Verlag,2011,92(3):225-242.

[6] Gonzalez O. Time integration and discrete Hamiltonian systems[J]. Journal of Nonlinear Science, 1996, 6 (5): 449-467.

[7] Mclachlan R I, Quispel G R W, Robidoux N. Geometric integration using discrete gradients[J]. Philosophical Transactions of the Royal Society B Biological Sciences, 1998, 357 (1754): 1 021-1 045.

[8] Celledoni E, Grimm R I, Mclachlan D I, et al. Preserving energy resp. dissipation in numerical PDEs using the average vector feild method[J]. Journal of Computational Physics, 2012, 231 (20): 6 770-6 789.

[9] Iavernaro F, Pace B. S-Stage trapezoidal methods for the conservation of Hamiltonian Funtions of Polynomial type[J]. AIP Conference Proceedings, 2007, 936 (1): 603-606.

[10] Quispel G R W, McLaren D I. A new class of energy-preserving numerical integration methods[EB/OL].[2017-06-10]. http://adsabs.harvard.edu/abs/2008JPhA...41d5206Q.

[11] Celledoni E, Mclachlan R I, Owren B, et al. On Conjugate B-series and their eometric structure[J]. European Society of Computational Methods in Sciences and Engineering, 2010, 5: 85-94.

[12] Cai J X, Wang Y S. A conservation Fourier pseudospectral algorithm for a coupled nonlinear Schrödinger system[J]. China Phys B, 2013, 22 (6): 135-140.

[13] Chen J B, Qin M Z. Multi-symplectic Fourier pseudospectral method for the nonlinear Schrödinger equation[J]. Electronic Transactions On Numerical Analysis, 2001, 12(11):193-204.

HighOrderDiscreteLineIntegralMethodfortheCoupledSchrödinger-KdVEquation

Chen Xiaowei, Sun Jianqiang

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

Based on the fourth order average vector field method and the Boole discrete line integral theory, the high order Boole discrete line integral method of the Hamiltonian system was proposed. The method was used to solve the energy conservation coupled Schrödinger-KdV equation, and a new high order scheme of the energy conservation coupled Schrödinger-KdV equation was obtained. The numerical results showed that the new scheme can simulate the evolution behaviors of the coupled Schrödinger-KdV equation very well; moreover, the discrete energy conservation property was also preserved.

coupled Schrödinger-KdV equation; high order discrete line integral method; Hamiltonian system

2017-07-01

国家自然科学基金项目(11561018)

陈宵玮(1993-)，女，安徽天长人，海南大学2015级硕士研究生，研究方向：微分方程数值解，E-mail: 838072754@qq.com

孙建强(1971-)，男，湖南双峰人，博士，教授，研究方向：微分方程数值解，E-mail: sunjq123@qq.com

1004-1729(2017)04-0303-07

O 241.8

ADOl10.15886/j.cnki.hdxbzkb.2017.0047