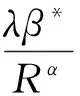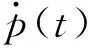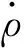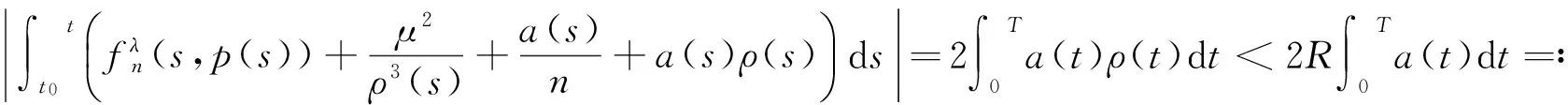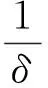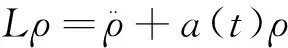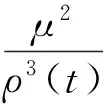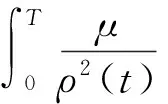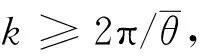具大角动量的奇异径向对称扰动系统的周期轨道

尹丽杰，王燕华，李胜军

(海南大学 信息科学技术学院, 海南 海口 570228)

具大角动量的奇异径向对称扰动系统的周期轨道

尹丽杰，王燕华，李胜军

(海南大学 信息科学技术学院, 海南 海口 570228)

应用拓扑度理论，首先研究了Hill方程奇异径向对称扰动系统周期轨道的存在性及轨道的运动特征，最后得到了在排斥奇异情形下大的角动量及大的向径旋转.

周期轨； 奇异径向对称系统； 拓扑度理论

考虑径向对称系统

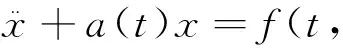
(1)

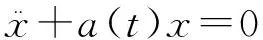
(2)

的非线性奇异径向对称扰动. 关于纯量奇异微分方程

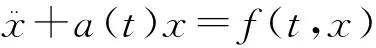
正周期解的存在性以及多重性已经吸引了诸多学者的关注，可以参考文献[2-5].

由于系统(1)的每个解x∶I→R2{0}在其最大存在区间I⊂R满足x(t)≠0，把系统(1)的解表示成极坐标的形式

x(t)=ρ(t)(cosφ(t),sinφ(t))，

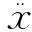
(3)

另一方面，近几年来关于径向对称开普勒型系统

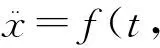
(4)

周期轨道的存在性问题，Fonda等在文献[6-11]中进行了研究，其中f允许在原点有奇异性. Fonda把系统用向径和角度来表示，并把角动量作为参数来考虑. 如文献[11]所述，自然界中的许多物理现象可用系统(4)来描述，例如描述引力场中物体运动的牛顿方程.

在文献[6-8]中考虑了如下系统

(5)

其中,c(t),e(t)是T-周期函数，γ≥1，得到如下定理[8].

定理1假设γ≥2，c是局部可积的T-周期函数,存在常数c1，c2使得

则对任意局部可积的T-周期函数e, 存在k1≥1,使得任意的正整数k≥k1, 系统(5)有周期解xk(t), 其最小周期为kT,且在一个周期里刚好转一圈, 即在极坐标意义下满足φ(t+kT)=φ(t)+2π.

当a(t)≡0时,系统(1)即为系统(4), 或者说, 系统(1)可以写成类似于系统(4)的形式

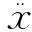
关于系统(1)和系统(4)的证明有本质上的区别，文献[6-11]中的结果不能包含笔者所需结果，并且既不需要Landesman-Lazer条件，也不需要非共振条件，但在文献[8-11]中，这些假设条件是必须的. 另一方面，考虑的是排斥奇异，而文献[7]处理的是吸引奇异(排斥奇异和吸引奇异有本质的不同[1]).

本文结果叙述如下

定理2假设Hill方程(2)有正的Green函数，且满足以下条件

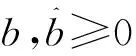
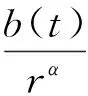
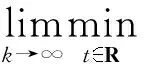
1 预备知识

假设Hill方程满足以下条件

(6)

的解ρ(t)可以表示为积分形式

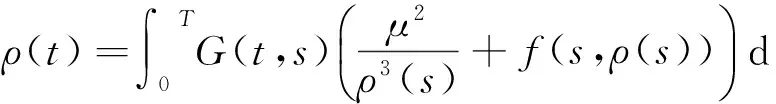
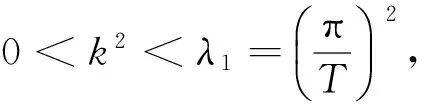
当假设条件(G)成立，引入如下记号

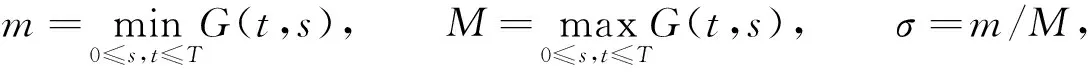
其中，M>m>0，0<σ<1.

相比于系统(4)，系统(1)有一个优势，就是可以直接利用等价系统(3)的Green函数的性质，为了证明本文结果，需要引理2和引理3，其中引理2是Leray-Schauder全局连续性原理[12].

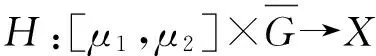
(7)

在[μ1,μ2]×∂G上无解，则方程(7)的解包含一条连接{μ1}×G与{μ2}×G的连通分支.

在叙述引理3之前，先介绍相关的符号和概念.

给定Banach空间X,Z分别为

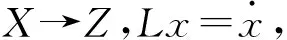
degLS(L-M0,Ω)=(-1)mdegB(F,Ω∩Rm,0),

其中，degLS，degB分别表示Leray-Schauder度和Brouwer度.

2 定理2的证明

2.1引理的证明定义截断函数fn∶R×R→R，

同时考虑一族方程

(8)

注意到ρ是方程(8)的T-周期解当且仅当ρ满足积分方程

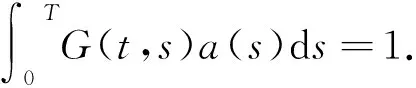
其次，证明μ足够大时，方程(8)有T-周期解. 为此，考虑同伦方程

(9)

和

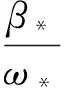
(10)

证明如果ρ是方程(9)的周期解，则ρ满足

因此，

证毕.

证明用反证法. 设ρn是方程

(11)

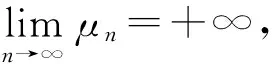
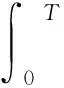
因此，

与μn→+∞矛盾.

证毕.

成立.

证明首先可以选取足够大的R>0，使得

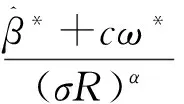
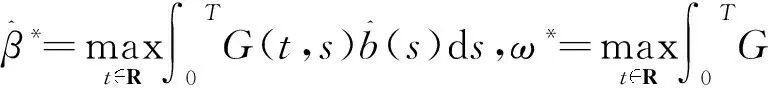
ρ(t)≥σ‖ρ‖≥σR.

另一方面，由于

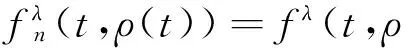
即与上面的假设相矛盾，因此‖ρ‖

其次又由条件(H), 得到

下面将证明，存在常数L>0，使得

于是，

证毕.

(12)

的解.

证明定义如下算子

L∶dom(L)⊂C1[0,T]→L1(0,T)，

和

N∶[A,B]×C1[0,T]→L1(0,T)，

容易知道式(12)的第一个方程等价于以下算子方程

Lρ=N(μ,ρ)，

由于Hill方程满足条件(G),L可逆，因此

ρ-L-1N(μ,ρ)=0.

(13)

定义

为了计算拓扑度，考虑同伦方程(9)，由引理6和同伦不变性，考虑方程(9)λ=0时的情况，即方程

等价于以下系统

其中，Y=(ρ,μ)，以及F(Y)定义为

由a(t)的正性和

可知F有唯一零点，设为(ρ0,μ0)，且其Jacobian行列式|JF(ρ0,u0)|>0，由引理3，I-L-1N(μ,·)的Leray-Schauder度等于F的Brouwer度，即

结论得证.

证毕.

将定义函数Φ:→R为

显然，Φ是连续函数，下面证明Φ的像是一个区间.

成立.

证明令(μ,ρ)是的元素且则

将上式两边积分，得

另一方面，

于是，

得到

证毕.

Φ(μ,ρ)=θ，

显然，ρ是T周期的，且式(3)的第一个方程成立. 定义

则φ(t)满足式(3)的第二个方程，且

即结论成立.

证毕.

因此，(ρ,μ)是系统(3)的解.

x(t+T)=x(t)exp(iθ)，

(14)

综上可知，定理2得证.

证毕.

[1] Lazer A, Solimini S. On periodic solutions of nonlinear differential equations with singularities[J]. Proc. Amer. Math. Soc., 1987 (99): 109-114.

[2] Ren J, Cheng Z, Siegmund S. Positive periodic solution for Brillouin electron beam focusing system[J]. Discrete Contin. Dyn. Syst. Ser. B, 2011 (16): 385-392.

[3] Jiang D, Chu J, Zhang M. Multiplicity of positive periodic solutions to superlinear repulsive singular equations[J]. Joumal of Differential Equations, 2005 (211): 282-302.

[4] Torres P J. Existence of one-signed periodic solutions of some second-order differential equations via a Krasnoselskii fixed point theorem[J]. J. Differential Equations, 2003 (190): 643-662.

[5] Torres P J. Non-collision periodic solutions of forced dynamical systems with weak singularities[J]. Discrete Contin. Dyn. Syst.,2004 (11): 693-698.

[6] Fonda A, Toader R. Periodic orbits of radially symmetric Keplerian-like systems: A topological degree approach[J]. Journal of Differential Equations, 2008 (244): 3 235-3 264.

[7] Fonda A, Urena A J. Periodic, subharmonic, and quasi-periodic oscillations under the action of a central force[J]. Discrete Contin. Dyn. Syst., 2011 (29): 169-192.

[8] Fonda A, Toader R. Periodic solutions of radially symmetric perturbations of Newt-onian systems[J]. Proc. Amer. Math. Soc., 2012 (140): 1 331-1 341.

[9] Fonda A, Toader R. Radially symmetric systems with a singularity and asymptotically linear growth[J]. Nonlinear Anal, 2011 (74): 2 485-2 496.

[10] Fonda A, Toader R. Periodic orbits of radially symmetric systems with a singularity: the repulsive case[J]. Adv. Nonlinear Stud, 2011 (11): 853-874.

[11] Fonda A, Toader R, Zanolin F. Periodic solutions of singular radially symmetric systems with superlinear growth[J]. Ann. Mat. Pura Appl. 2012 (191) : 181-204.

[12] Zeidler E. Nonlinear functional analysis and its applications[M]. New York: Springer, 1986.

PeriodicOrbitsofSingularRadiallySymmetricSystemswithALargeAngularMomentum

Yin Lijie, Wang Yanhua, Li Shengjun

(College of Information Sciences and Technology, Hainan University, Haikou 570228, China)

In the report, the theory of topological degree was used to study the existence of periodic orbits of radically symmetric systems with a repulsive singularity. The periodic orbits rotate around the origin with both large angular and large amplitude was obtained.

periodic orbits; singular radically symmetric systems; topological degree theory

2017-10-10

国家自然科学基金(11461016)；海南省自然科学基金(117005)；海南省高等学校教育教学改革研究(Hnjg2017-6)；海南大学青年基金(hdkyxj201718)

尹丽杰(1993-), 女, 山东德州人,海南大学2016级硕士研究生, 研究方向:变分与拓扑方法,E-mail:18315913978@163.com.

李胜军(1976-), 男, 湖南娄底人,副教授,博士,研究方向：泛函算子理论研究, E-mail: shjli626@126.com

1004-1729(2017)04-0295-08

O 177

ADOl10.15886/j.cnki.hdxbzkb.2017.0046