一种二值图像物体形状特征计算方法
2018-01-11何立风高启航
何立风, 高启航, 赵 晓, 姚 斌
(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)
0 引言
二值图像连通域(物体)的形状特征提取是物体识别、图像分析和计算机视觉等领域不可或缺的处理.连通域的形状特征一般包含面积、周长、圆形度和重心等[1-3].连通域形状特征的计算一般以连通域标记算法为前提.首先要对图像中的各个连通域用不同的标号进行标记,再根据标号对各个连通域进行形状特征的计算.主流的连通域标记算法[4]有以下两类:
(1)标号传播算法[5,6].该类算法首先寻找一个未标记的像素,将其用一个新的标号进行标记,再用该标号标记该像素所在连通域的所有其他像素.此类算法中最高效的是文献[6]中提出的基于边界追踪的连通域标记算法.
(2)基于等价标号解析的算法[7-17].此类算法按照扫描像素的次数可分为多次扫描[7,8]、二次扫描[9-16]和四次扫描[17]算法.首先,对扫描中遇到的前景像素分配一个暂定标号并将属于同一连通域的不同暂定标号记录为等价标号(同一连通域上的所有暂定标号都将是等价标号).其次,通过解析等价标号关系,将等价标号中的最小标号作为该连通域所有暂定标号的代表标号.最后,将各个像素的暂定标号用其代表标号进行替换,得到最终的标号.
针对现有的物体形状特征提取的方法[1-3]只能处理不含孔洞的物体的局限性,本文提出一种计算含有孔洞的物体的形状特征的算法.在上述的连通域标记算法中,文献[6]中提出的基于边界追踪的连通域标记算法可以在进行标记的同时提取连通区域的边界,并具有一次标记、标号值不会改变且标号值连续的特点.本文提出的算法是在基于边界追踪的连通域标记算法的基础上,融合了物体形状特征计算.实验结果表明本算法能有效地进行连通域标记和物体形状特征提取.
1 背景知识
M×N的二值图像I(M,N)在(x,y)处的像素及其值用p(x,y)表示,其中0≤x 连通域标记示意图如图1所示.经过标记的图像,每个连通域上的像素都由一个相同的标号(数字)标记,不同的连通域代表不同的物体,具有不同的标号.由于二值图像中的前景像素值为1,所以为了区分标号值与原始二值图像的前景像素值,在基于边界追踪的连通域标记算法中,连通区域的标号取2以上的整数. 图1 连通区域标记示意图 连通区域基本形状特征主要有面积、周长、圆形度和重心等[2]. (1)面积 面积的定义:连通域内所有像素的个数,用A表示. (2)周长 图2 四种边界模式 (3)圆形度 圆形度是衡量连通域形状的重要特征,是表示连通域圆形程度的指标,值介于0和1之间,用C表示.圆形度的计算与连通域的面积与周长有关.如果连通域中含有孔洞,则计算圆形度时的面积包括孔洞面积H.圆形度的计算公式如下所示: C=4π·(A+H)/P2 (1) 从公式(1)中可以看出,当C=1时,连通区域即为圆形;C越小,连通区域与圆形差距越大. (4)重心 连通区域的重心和中心含义相同,用所有像素点的中心位置表示.中心位置即所有坐标点的行和列的坐标值的平均值.设重心坐标为(X,Y),计算公式如下所示: (2) (3) 连通域形状特征的计算是基于连通域标记算法的.边界追踪标记算法是连通域标记算法中的一种典型算法,该算法能同时完成连通域标记和连通域边界提取.边界追踪标记算法的大致思路是:从上到下、从左到右扫描图像像素,当扫描到前景像素时,按照下面四个步骤处理: (1)当扫描到的前景像素是未标记的外边界像素Aout时,首先用一个新的标号l标记该像素,然后从该像素出发进行外边界追踪操作直到回到像素Aout,用相同的标号l标记这个连通域的外边界上所有的像素,如图3(a)所示; (3)当扫描到的、已标记过的前景像素是未经内边界追踪处理过的内边界像素Ain时,从该像素出发进行内边界追踪操作直到回到像素Ain,并用Ain的标号标记该内边界上的所有像素,如图3(c)所示; (a) 未标记的外边界 (b) 已标记的外边界 (c) 未处理的内边界 (d) 已处理的内边界图3 边界追踪标记步骤示意图 另外,在以上四个步骤中,当进行外边界追踪时,用-1标记与边界像素邻接的背景像素,在图3中用“-”表示;在进行内边界追踪时,用-2标记与边界像素邻接的背景像素,在图3中用“*”表示. 算法中的边界追踪方法简述如下: 边界追踪的目的是找到连通域的外边界或内边界.边界追踪的大致思路为:设P为边界追踪的起始当前像素,初始检查方向为K.如果P是一个孤立像素,则结束追踪;否则,从K方向开始沿顺时钟方向检查该方向上的P的邻接像素,如果检查中的邻接像素为前景像素,则该像素也是边界像素,把该像素作为当前像素继续(重复)边界追踪处理,直到下列两个条件同时得到满足时终止:①当前像素为起始像素P;②检查方向与起始像素P的初始检查方向K一致. 外边界追踪与内边界追踪的唯一区别在于初始检查方向不同.方向标号表示图如图4所示.外边界追踪的初始方向为起始像素P的正上方,在图4中为像素A0的方向;内边界追踪的初始方向在P的正下方,在图4中为像素A4的方向. 图4 方向标号表示图 在使用边界追踪标记算法对连通域进行标记时,需要对连通域的边界进行追踪.在进行边界追踪的同时,可以计算连通域的边界长(周长),这为计算连通域的形状特征提供了极大的方便.如上所述,连通域的形状特征包括面积、周长、圆形度和重心.根据前述形状特征的定义,可在边界追踪标记的基础上按照下列方法计算连通域的形状特征: (1)连通域的面积为连通域上所有像素个数之和,所以只须在连通域标记过程中添加对每一个标号的像素的计数操作,就可以在结束图像扫描时完成所有连通域的面积计算; (2)连通域的周长为外边界的长度,因此可以在对连通域进行外边界追踪的过程中同时计算该连通域的周长; (3)重心坐标是连通域内所有像素点的坐标的平均数,所以在标记连通域时,对同一标号的像素的横纵轴坐标分别进行累加,在标记结束后用相应的累加值除以该连通域的面积就可得到重心坐标; (4)圆形度与连通域的面积、连通域内的孔洞面积以及连通域的外周长有关,由公式(1)计算.各个连通域的面积和连通域的外周长可由上述(1)和(2)分别获得.而各个连通域的孔洞面积可以在标记结束后,通过再次扫描图像计算. 算法的伪代码如下: 算法:使用边界追踪标记算法计算连通域基本形状特征 InitializeA,H,P,C,X,Y←0 l=2 x=0,y=0 Whiley |Whilex | |Ifp(x,y)==1 | | |Ifp(x,y)是未被标记的外边界像素 | | | |OuterTrace(p(x,y),l) | | | |Ifp(x,y)是未被内边界追踪处理过的 | | | | 像素 | | | | |InnerTrace(p(x,y),l) | | | |EndIf | | | |l++ | | |Else | | | |Whilep(x,y)==1 | | | | |Ifp(x,y)是未被标记的内边界像素 | | | | | |InnerTrace(p(x,y),p(x-1,y)) | | | | |Else | | | | | |p(x,y)=p(x-1,y) | | | | | |A[p(x,y)]+=1 | | | | | |X[p(x,y)]+=x,Y[p(x,y)]+=y | | | | |EndIf | | | | |x++ | | | |EndWhile | | |EndIf | |x++ |EndWhile |y++ EndWhile % 计算孔洞面积 x=0,y=0 Whiley |Whilex | |Ifp(x,y)属于标号m的孔洞部分: | | |H[m]+= 1 | |EndIf |EndWhile EndWhile % 计算各个连通域的圆形度和重心 i=2 Whilei |C[i]=4π*(A[i]+H[i])/(P[i]∧2) |X[i]/=A[i],Y[i]/=A[i] EndWhile 在执行外边界追踪函数OuterTrace时,从像素p(x,y)开始沿外边界追踪边界像素,边标记边计算累加面积和周长,并将检查到的背景像素标记为-1.该函数伪代码如下: FunctionOuterTrace(p(x,y),l) |For从像素p(x,y)开始的外边界追踪处理中 | | 的每个当前像素p(u,v) | |Ifp(u,v)是背景像素 | | |p(u,v)=-1 | |Else | | |p(u,v)=l | | |A[l]+=1 | | |X[l]+=x,Y[l]+=y | | |Ifp(u,v)与前一个外边界像素在同行或 | | | 同列 | | | |P[l]+=1 | | |Else | | |EndIf | |EndIf |EndFor End 由于连通域内边界与周长无关,所以在执行内边界追踪函数InnerTrace时,不需要计算周长,其伪代码如下: FunctionInnerTrace(p(x,y),l) |For从像素p(x,y)开始的内边界上追踪处理 | 中的每一个当前像素p(u,v) | |Ifp(u,v) 是背景像素 | | |p(u,v)=-2 | |Else | | |p(u,v)=l | | |A[l]+=1 | | |X[l]+=u,Y[l]+=v |EndFor End 第一次扫描完毕后,对于标号为l的连通域,其面积和外周长分别为A[l]和P[l];重心的横纵坐标可分别由X[l]=X[l]/A[l]和Y[l]=Y[l]/A[l]计算.由于在对标号为l的连通域的内边界追踪时将扫描到的背景像素用-2标记,孔洞部分可以看作以-2为边界的背景像素的连通域.在第二次扫描中,统计孔洞部分的像素个数就能得到相应的孔洞面积.这样,标号为l的连通域的圆形度C[l]可由C[l]=4π*(A[l]+H[l])/(P[l]∧2)计算.如果连通域不含孔洞,则在第二次扫描中不会做任何处理,所以算法也同样适用于不含孔洞的连通域形状特征的计算. 为了验证本文提出的计算物体特征算法的有效性,在图5(a)所示的测试图像进行了测试.算法程序用C语言编写,编译环境为GCC 5.4.0,操作系统为Ubuntu14.04 64位.计算机硬件配置为:Intel i5-3470 3.2 GHz双核处理器,4 GB内存.图5(b)是经过连通域标记的图像,每个连通域上方的数字代表其标号值.表1为各个连通域(物体)的各种形状特征的计算结果.算法在测试图像上运行500次的平均运行时间为7.36毫秒. (a) 测试图像 (b) 带标号的图像图5 测试图像与标记后的图像 标号周长面积孔洞面积重心(X)重心(Y)圆形度21228.7775949211922056880.813867.5041440126222912360.9041002.015718605317110.7251266.0064525282716022660.736984.192761148767897200.427711.972799286258682370.91 基于边界追踪的连通域标记算法只需扫描图像一次.在扫描过程中,非边界像素只访问一次,边界像素被访问的次数不超过4次,因此算法在线性时间内完成[6],时间复杂度为O(n),其中n为图像的像素个数.本文提出的算法在第一次扫描图像时,与连通域标记算法对像素的扫描方式和访问模式相同,在第二次扫描时,只对孔洞区域进行处理,故本文算法的时间复杂度也为O(n). 基于边界追踪的连通域标记算法在原始图像上完成标记,不需要占用额外空间,因此其空间复杂度为O(1).本文连通域形状特征计算方法与此标记算法相比只需要存储各个连通域的形状特征量等,故算法所占空间仅依赖于连通域的数量.由于像素个数为n的图像的最大连通域的数量为n/4[11],因此本文算法的空间复杂度为O(n). 本文在基于边界追踪的连通域标记算法的基础上,首次提出了一种计算二值图像中含孔洞物体的形状特征的算法.本文提出的计算含有孔洞的物体的形状特征的算法优点有:①可以同时进行连通域标记和形状特征的计算;②除了计算连通域的形状特征,算法还可以直接提取连通域的边界;③本文算法在线性时间和线性空间内完成;④本文算法可扩展性好,经过简单扩展还可应用于欧拉数、密度等其他形状特性的计算.实验结果表明本算法可以有效的计算二值图像中含有孔洞的连通域的基本形状特征. [1] Rafael Gonzalez,Richard Woods.数字图像处理[M].3版.阮秋琦,阮宇智.北京:电子工业出版社,2017. [2] Richard Szeliski.计算机视觉:算法与应用[M].1版.艾海舟,兴军亮.北京:清华大学出版社,2012. [3] David Forsyth,Jean Ponce.计算机视觉——一种现代方法[M].2版.高永强.北京:电子工业出版社,2017. [4] He L,Ren X,Gao Q,et al.The connected-compo-nent labeling problem:A review of state-of-the-art al-gorithms[J].Pattern Recognition,2017(70):25-43. [5] Hu Q,Qian G,Nowinski W L.Fast connected-component labelling in three-dimensional binary images based on iterative recursion[J].Computer Vision and Image Understanding,2005,99(3):414-434. [6] Chang F,Chen C J,Lu C J.A linear-time compo-nent-labeling algorithm using contour tracing technique[J].Computer Vision and Image Understanding,2004,93(2):206-220. [7] He L,Chao Y,Suzuki K.A run-based one-and-a-half-scan connected-component labeling algorithm[J].International Journal of Pattern Recognition and Artificial Intelligence,2010,24(4):557-579. [8] 冯海文,牛连强,刘晓明.高效的一遍扫描式连通区域标记算法[J].计算机工程与应用,2014,50(23):31-35. [9] Wu K,Otoo E,Shoshani A.Optimizing connected component labeling algorithms[C]//Proceedings of the 19th International Conference on Information Processing in Medical Imaging. Glenwood:IEEE,2005:1 965-1 976. [10] He L,Chao Y,Suzuki K.A run-based two-scan labeling algorithm[J].IEEE Transactions on Image Processing,2008,17(5):749-756. [11] He L,Chao Y,Suzuki K,et al.Fast connected-component labeling[J].Pattern Recognition,2009,42(9):1 977-1 987. [12] 谢宜壮,谭许彬,陈 禾.一种新的连通域标记算法[J].北京理工大学学报,2012,32(12):1 273-1 278. [13] Zhao X,He L,Yao B,et al.A new connected-component labeling algorithm[J].IEICE Transactions on Information & Systems,2015(11):2 013-2 016. [14] 牛连强,彭 敏,孙忠礼,等.利用游程集合的标号传播实现快速连通域标记[J].计算机辅助设计与图形学学报,2015,27(1):128-135. [15] Grana C,Borghesani D,Cucchiara R.Fast block based connected components labeling[C]//Proceedings of the International Conference on Image Processing.Cairo:IEEE,2009:4 061-4 064. [16] He L,Chao Y,Zhao X,et al.Configuration-transition-based connected-component labeling[J].IEEE Transactions on Image Processing,2014,23(2):943-951. [17] Suzuki K,Horiba I,Sugie N.Linear-time connected-component labeling based on sequential local operations[J].Computer Vision and Image Understanding,2003,89(1):1-23.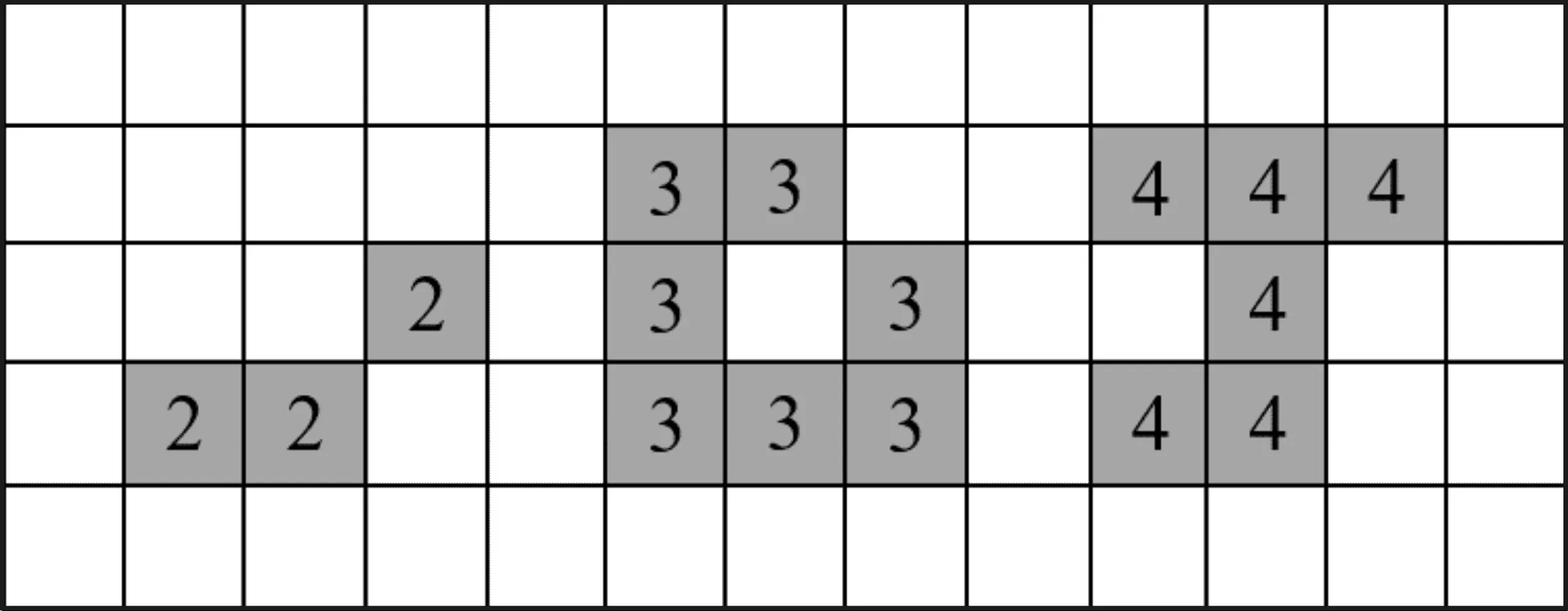
1.1 连通域基本形状特征的定义
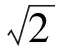
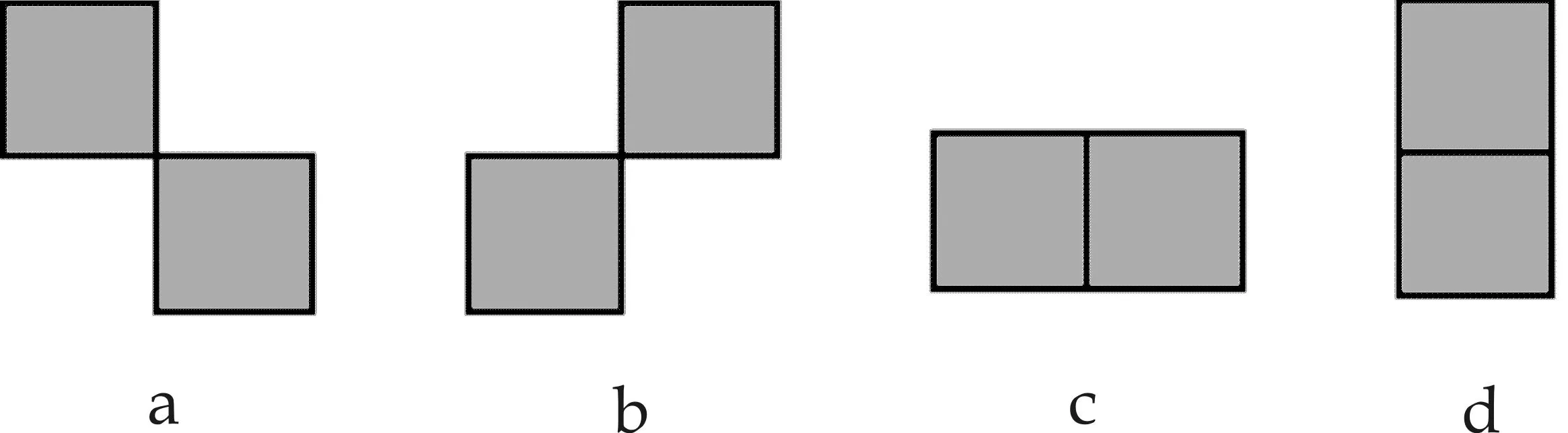


1.2 边界追踪标记算法
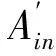

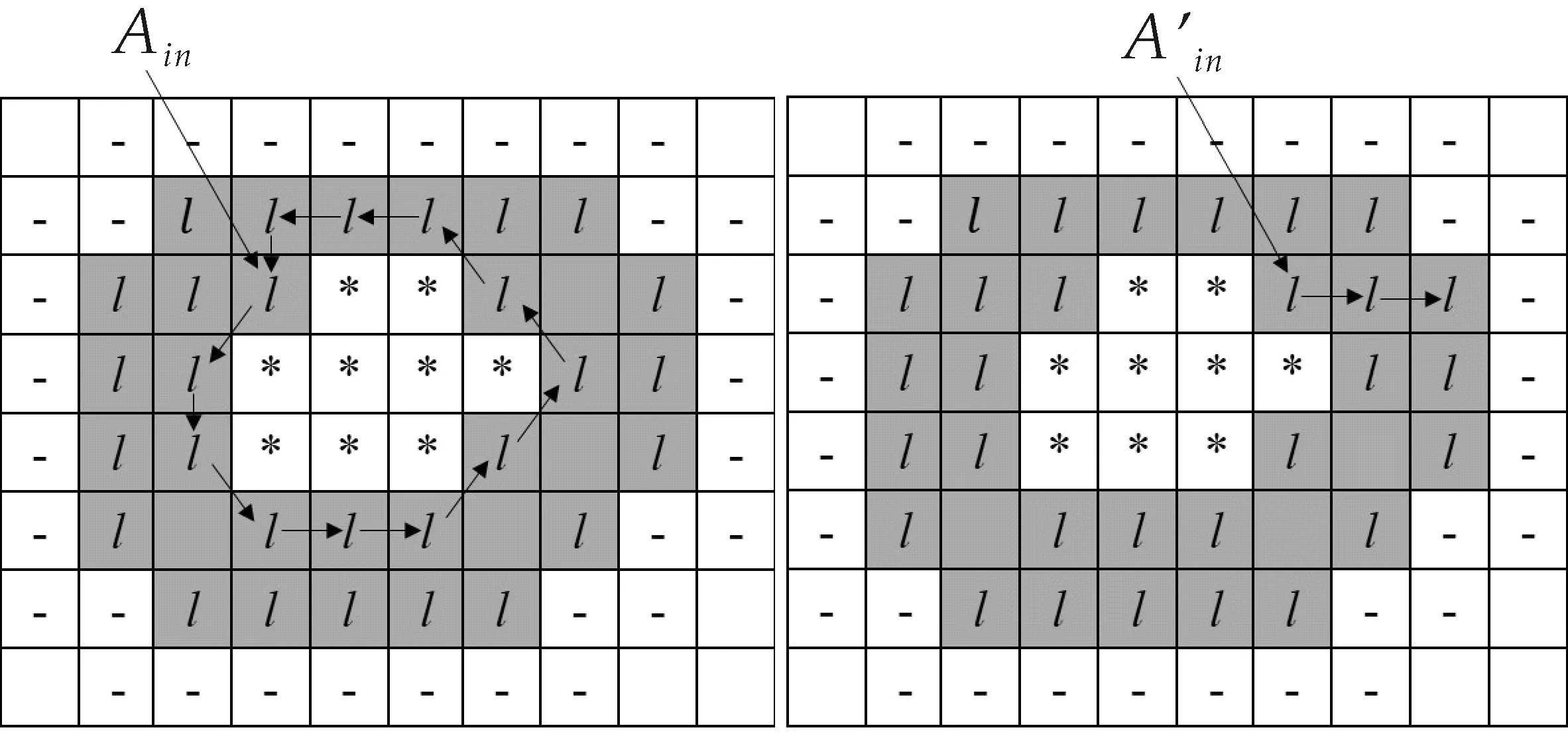
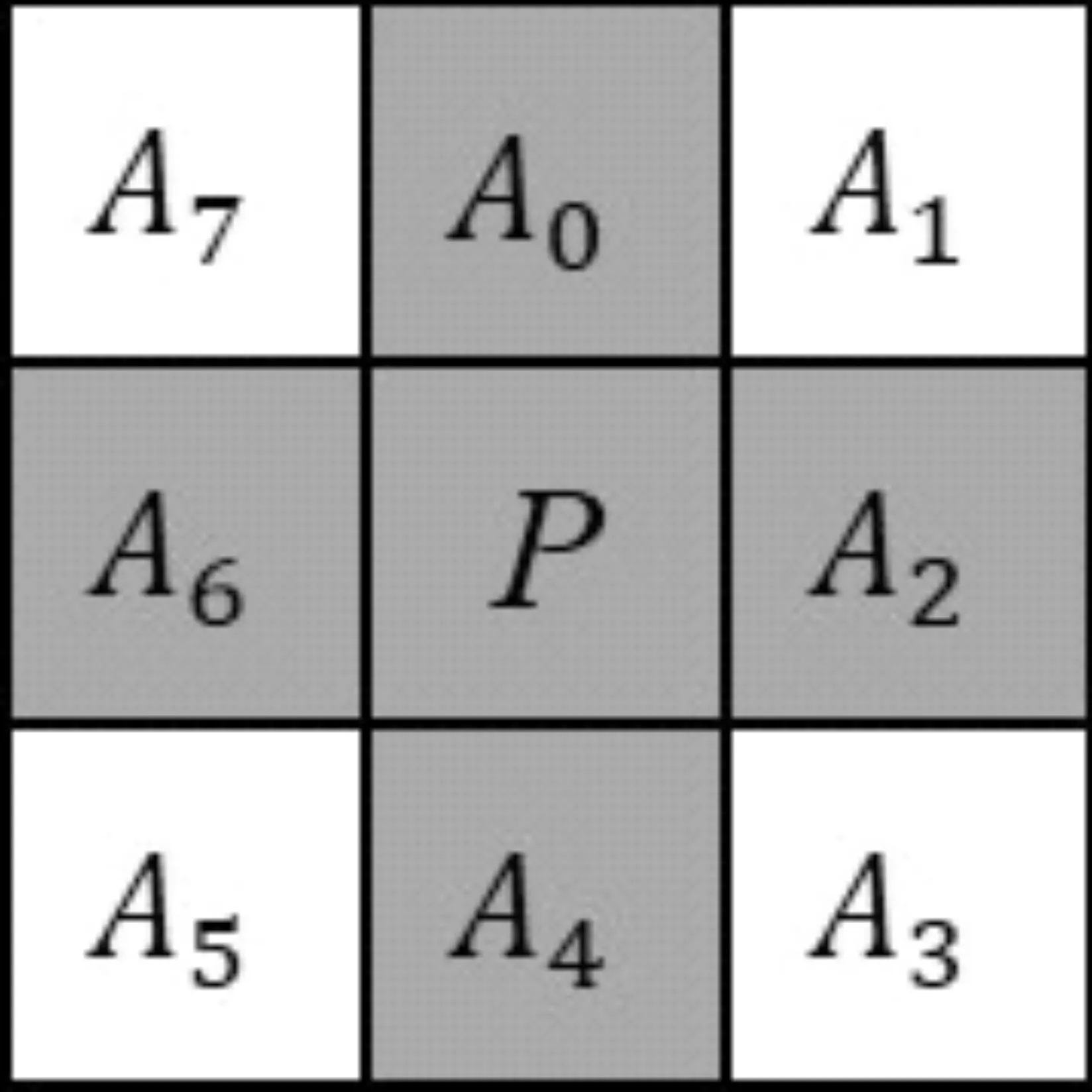
2 基于边界追踪的连通域形状特征计算方法
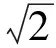
3 实验结果


4 算法性能分析
5 结论
