另辟蹊径有效引导化繁为简

孙小军

[摘 要]切割填补法、容斥原理法、等积转化法、旋转移动法、重新构图法等是将一般图形转化为特殊图形常用的方法，这些方法能使抽象问题具体化、复杂问题简单化，提高学生的数学素养，值得教师重视。

[关键词]几何图形；转化；一般；特殊；构图

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）35-0065-02

求稍复杂的阴影部分的面积，是小学“图形与几何”的重点和难点。解决这类问题关键在于因题制宜，将一般图形转化为特殊图形。常用方法有以下五种。

一、切割填补法

切割填补法是通过观察阴影部分与整体图形之间的关系，添加辅助线，切割某个部分填补整体，从而使不规则图形变为规则图形。这一方法最为常用、最具代表性，也最为简单有效。

【例1】如图1，四分之一圆的半径为10厘米，以它的两条半径为直径，在内部作两个半圆，求阴影部分的面积。

分析：图1中的阴影部分比较规则，观察它的特征，发现通过添加辅助线进行切割，再整体填补，图1的阴影部分就转化为图2中的阴影部分，所以所求阴影部分的面积实际就是等腰直角三角形（如图2阴影部分）的面积：S=10×10÷2=50（平方厘米）。

二、容斥原理法

对于比较规则的图形，用切割填补法虽然也能解决问题，但是却大费周折、浪费时间。这时运用容斥原理法，可以省时省力，事半功倍。

【例2】如图3，正方形的边长为8厘米，求图中阴影部分的面积。

分析：图3是正方形中套着四个半圆，四个半圆相加就得到2个完整的圆，在这个过程中每个阴影部分被加了两次，减去一个正方形，正好得到阴影部分的面积，那么阴影部分的面积就是S=3.14×4×4×2-8×8=36.48（平方厘米）。

【例3】求圖4阴影部分的面积。（单位：厘米）

分析：图4是由直径为6厘米和8厘米的两个半圆和一个直角三角形组成的，单独求阴影部分面积比较困难。认真观察图形后发现，阴影部分的面积等于直径是6 厘米和8厘米的两个半圆加一个直角三角形的面积减去直径是10厘米的大半圆的面积，即S=3.14×（3×3+4×4）÷2+6×8÷2-3.14×5×5÷2=24（平方厘米）。

三、等积转化法

这个方法与切割填补法类似，都是在忠于题意的前提下实现对图形的转化，通过点的移动，改变原有图形的形状，但是阴影部分的面积却不变，实现的是等积变换。

【例4】如图5，已知一大一小两个正方形拼凑在一起，大正方形的边长为8厘米，求阴影部分的面积。

分析：题目并没有告知小正方形的边长，因此要想方设法将所求阴影部分转化到大正方形中，如图6。连接AB，得AB[?]CD，因此点A和点B到CD的距离相等，得S△ACD=S△BCD，即原来的阴影部分的面积总和保持不变。S=[14][π]r2=3.14×8×8÷4=50.24（平方厘米）。

【例5】如图7，求阴影部分的面积。（单位：厘米）

分析：图中阴影部分是一个梯形，它的上底、下底和高都不知道，显然无法直接求出它的面积。因此，要想方设法将其转化为求另一个图形的面积。观察可知，平行四边形BCDG的面积等于长方形ABCE的面积（等底等高），两者都减去同一个三角形BCF，所以阴影部分的面积等于梯形ABFE的面积（如图8），即S=（2+6）×4÷2=16（平方厘米）。

四、旋转移动法

一些图形的阴影部分比较杂乱分散，看似毫无章法，但是进行适当旋转、移动后重新组合在一起，就可以得到一个较为简单的新图形。

【例6】如图9，已知大圆的半径等于小圆的直径，大圆的半径为4厘米，求阴影部分的面积。

分析：图9中阴影部分分为三小块，分别求出各部分的面积再相加非常困难。仔细观察发现，可以将图形旋转拼凑为图10，阴影部分形如一个“逗号”，而整个大圆可以分成四个“逗号”（如图11），那么阴影部分的面积就是整个大圆的[14]，即S=[14][πr2]=3.14×4×4÷4=12.56（平方厘米）。

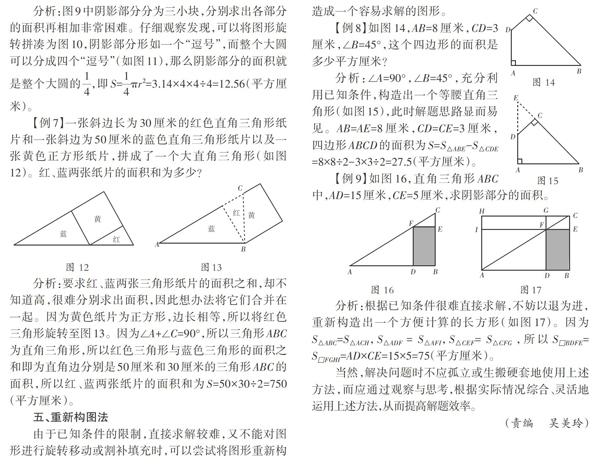
【例7】一张斜边长为30厘米的红色直角三角形纸片和一张斜边为50厘米的蓝色直角三角形纸片以及一张黄色正方形纸片，拼成了一个大直角三角形（如图12）。红、蓝两张纸片的面积和为多少？

分析：要求红、蓝两张三角形纸片的面积之和，却不知道高，很难分别求出面积，因此想办法将它们合并在一起。因为黄色纸片为正方形，边长相等，所以将红色三角形旋转至图13。因为∠A+∠C=90°，所以三角形ABC为直角三角形，所以红色三角形与蓝色三角形的面积之和即为直角边分别是50厘米和30厘米的三角形ABC的面积，所以红、蓝两张纸片的面积和为S=50×30÷2=750（平方厘米）。

五、重新构图法

由于已知条件的限制，直接求解较难，又不能对图形进行旋转移动或割补填充时，可以尝试将图形重新构造成一个容易求解的图形。

【例8】如图14，AB=8厘米，CD=3厘米，∠B=45°，这个四边形的面积是多少平方厘米？

分析：∠A=90°，∠B=45°，充分利用已知条件，构造出一个等腰直角三角形（如图15），此时解题思路显而易见。AB=AE=8厘米，CD=CE=3厘米，四边形[ABCD]的面积为S=S△ABE-S△CDE=8×8÷2-3×3÷2=27.5（平方厘米）。

【例9】如图16，直角三角形ABC中，AD=15厘米，CE=5厘米，求阴影部分的面积。

分析：根据已知条件很难直接求解，不妨以退为进，重新构造出一个方便计算的长方形（如图17）。因为S△ABC=S△ACH，S△ADF = S△AFI，S△CEF= S△CFG ，所以S□BDFE= S□FGHI=AD×CE=15×5=75（平方厘米）。

当然，解决问题时不应孤立或生搬硬套地使用上述方法，而应通过观察与思考，根据实际情况综合、灵活地运用上述方法，从而提高解题效率。

（责编 吴美玲）