基于ADAMS的1 t电动平衡吊失衡力分析及解决方法

张 彦, 张文强

(合肥工业大学 机械工程学院,安徽 合肥 230009)

基于ADAMS的1 t电动平衡吊失衡力分析及解决方法

张 彦, 张文强

(合肥工业大学 机械工程学院,安徽 合肥 230009)

由杆件自重引起的失衡力对平衡吊的随遇平衡有着极大的不利影响。文章以1 t电动平衡的设计参数为基础,建立了数字化模型,并利用ADAMS虚拟样机软件对失衡力的影响因素及变化趋势进行了研究;提出了一种通过改变水平导轨形状来降低失衡力的改进方案,并选取失衡力较为显著的某一极限位置建立了一系列不同梯度的模型加以验证。由分析结果可以得出,对水平导轨适宜变形可以有效地将失衡力降低至合理范围内,以保障平衡吊的随遇平衡。

平衡吊;随遇平衡;失衡力;水平导轨;极限位置

电动平衡吊是一种应用广泛的机械助力设备,具有结构简单、操作灵活、价格低廉、维护方便等特点,因而多见于车间、码头等需要频繁装卸的工作场合。

理论上说,平衡吊在其工作区间内无论是否悬挂重物都可以在任意时刻、任意位置达到平衡静止的状态,即随遇平衡状态[1]。然而,在实际工作中平衡吊由于杆系的自重、变形以及尺寸误差的影响,会使平衡吊在某些位置不能随遇平衡而产生滑移。对平衡吊失衡问题的研究已有了许多进展,如通过精确装配以减小径向操作力[2];通过对杆件的优化设计及加强筋的合理布置以减少变形;通过在实际应用中将摩擦力限制在某一范围内以获得最优性能等。而对于吊重达1 t以上的平衡吊,由于失衡力造成的影响非常明显,采用原有的弹簧平衡法[3]和重锤平衡法[4]所能起到的作用十分有限。针对这一问题,本文对某型号1 t平衡吊进行数字化建模及动力学仿真[5-9],分析自重引起的失衡力大小及其影响因素,并提出结构改进方案。

1 平衡吊工作原理及随遇平衡特性

平衡吊工作机构可简化为一平面四杆机构,如图1所示。4根杆由铰链连接,水平滑块和竖直升降件可分别在C处水平槽和A处竖直槽内滑动,以实现重物的移动和升降。

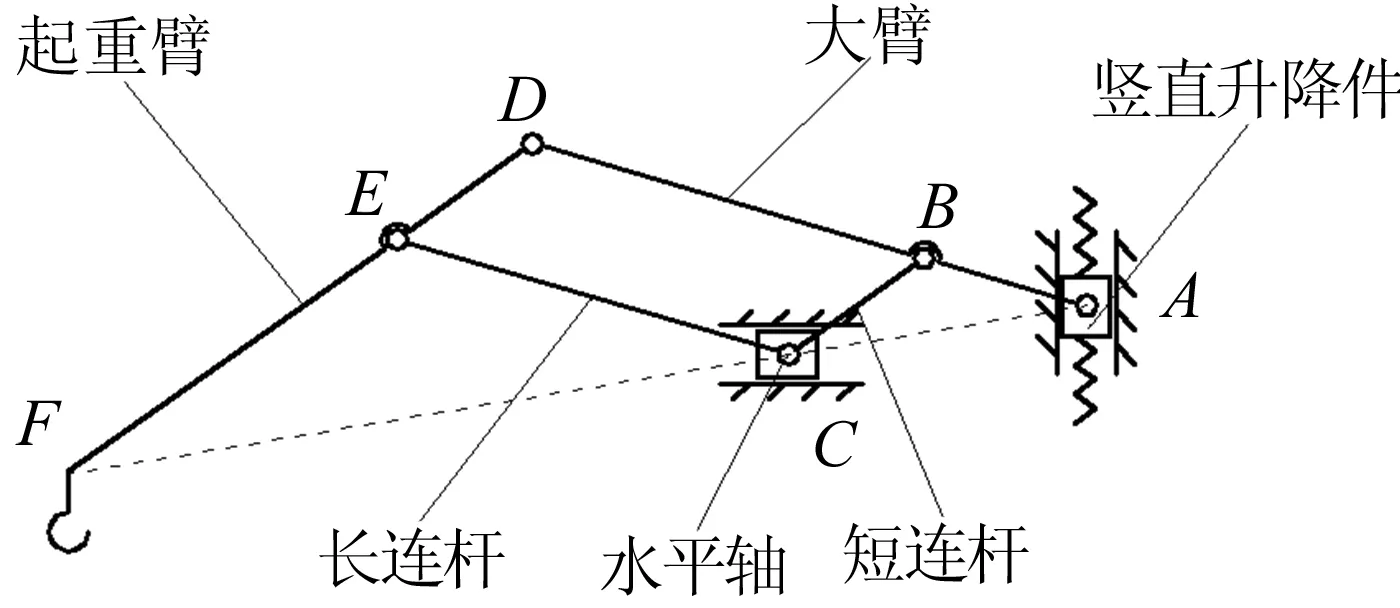
图1 平衡吊工作机构结构简图

为实现随遇平衡杆系需满足杆长条件[10]为:

AD/AB=DF/DE=m

(1)

其中，m为平行四边形放大系数。在不计杆件自重及杆件负载变形的基础上,满足(1)式的平衡吊均可保证随遇平衡。在此,可将杆系视为特殊的杠杆机构,并有以下特性:① 当平移重物时,若在F点水平移动距离X,则C点将同向移动x=X/m的距离;② 若作用在F点的水平力为f,则在C点受力大小为f/m;③ 当竖直起吊重物时,若F点需竖直移动距离Y,A点只需移动y=Y/(m-1)即可;④ 若提升的重物重力为G,A点受力大小为(m-1)G。

根据经验,m值取在5～10之间。当取值较大时,对于提高工作效率、减轻工作强度有较大帮助,但对各杆件的强度要求较高,因此多用于轻载平衡吊。本文所研究的1 t平衡吊,由于载重量较大,选取m=5以获得较好的受力条件,减小杆件变形量。

2 平衡吊动力学仿真及失衡力分析

2.1 模型动力学仿真

为细致分析杆件自重对失衡力的影响,并提出有效的减少失衡力的改进方案,现以某型号1 t平衡吊结构为基础,进行数字化建模分析。平衡吊结构布局及极限位置如图2所示。

由以往经验可知,当平衡吊处于4个极限位置时,失衡情况最为严重,因此按以上步骤分别建立位于下内、下外、上内状态的模型。将其导入ADAMS软件中,对各零件赋值[11]并在起重臂末端F处施加一速度为0.1 m/s水平驱动motion1,以模拟正常工作时水平移动的状态,并对模型进行仿真运行。

对于仿真结果来说,失衡力是无法直接体现的,但可以通过测试motion1的驱动力M间接求得。由于未设置摩擦系数,motion1为实现匀速运动所施加的力全部用于克服失衡力,需要注意的是motion1处测得的力F为失衡力作用在点F处的效果,两者间有一个放大倍数m的关系,即5F与失衡力等大反向。为叙述方便,下文出现的数值均为F点测得的数值。

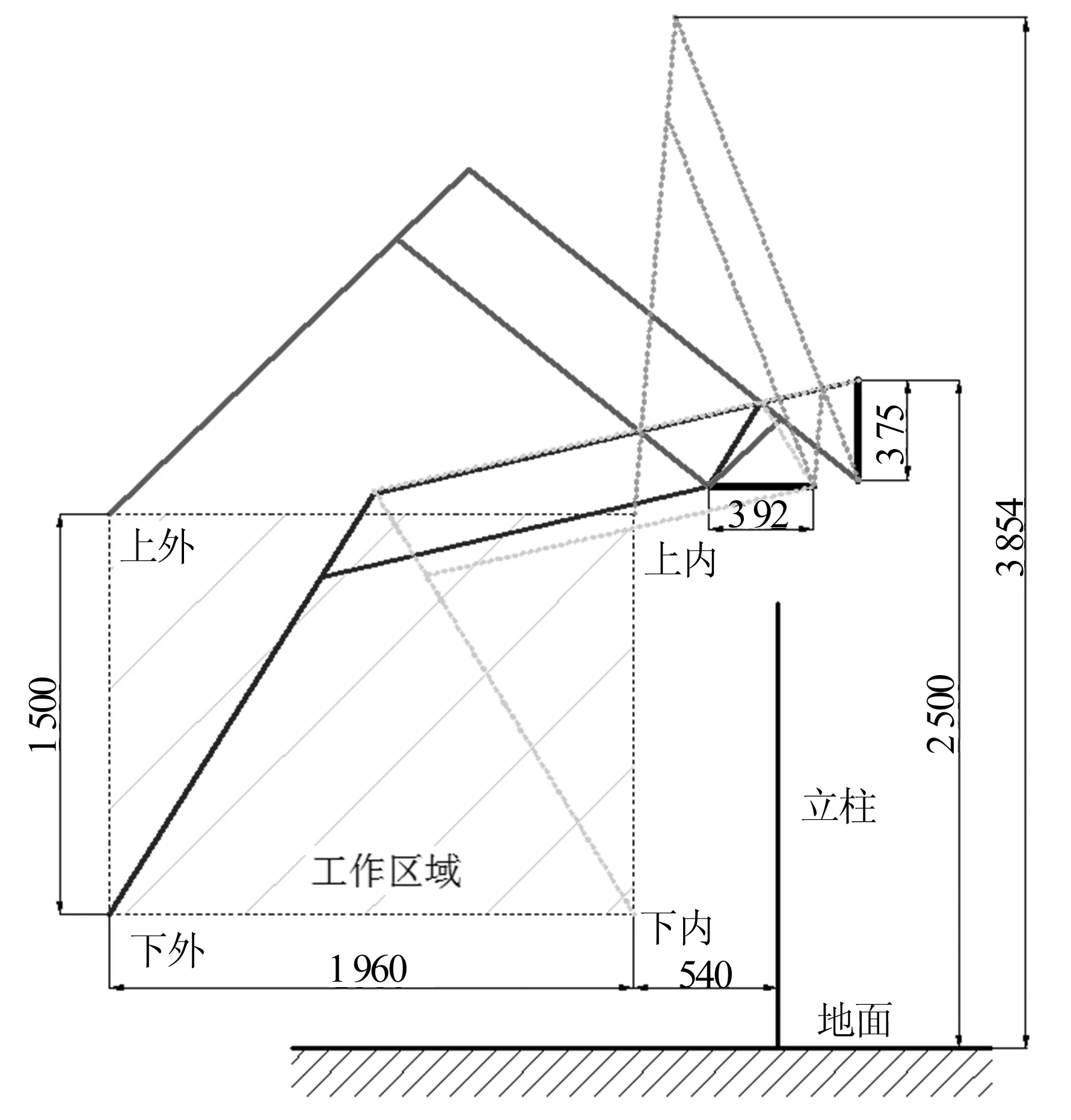
图2 1 t平衡吊结构布局

为探究移动速度与失衡力的关系,将下外模型的驱动速度分别设置为0.1、0.2 m/s进行仿真。仿真结果如图3所示,模型起始位置依次为下内、下外和上内状态。3个模型4次仿真所测得的失衡力数据见表1所列。

比较仿真1与仿真2曲线可知,平衡吊进行水平运行时,失衡力的大小与运动方向无关;比较仿真2与仿真3曲线可知,失衡力大小与运行速度无关;比较仿真1与仿真4曲线可知,平衡吊处于较低工作位置时失衡力更大。因此,下文均以平衡吊处于下内位置时的状态为基准模型。

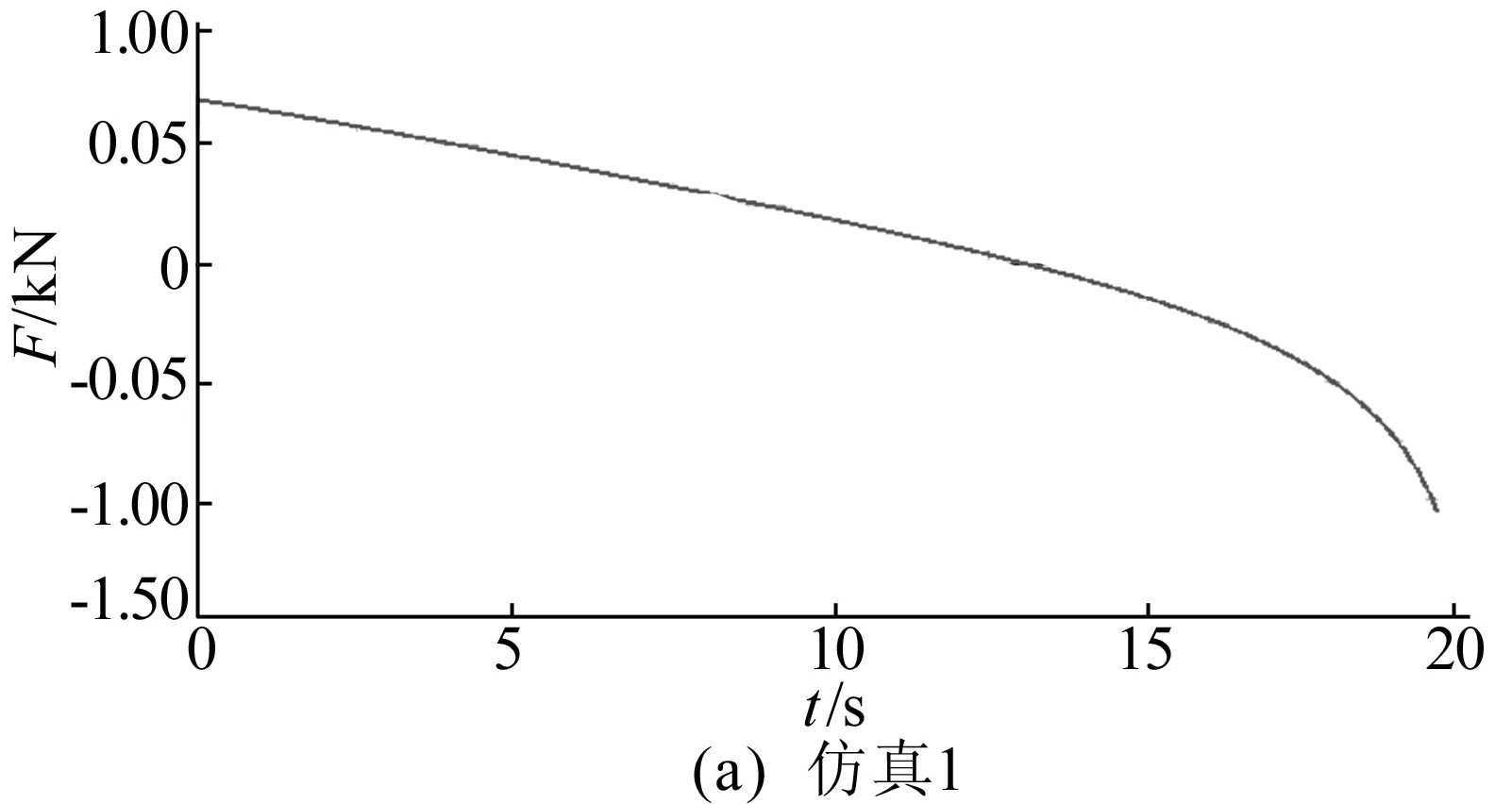
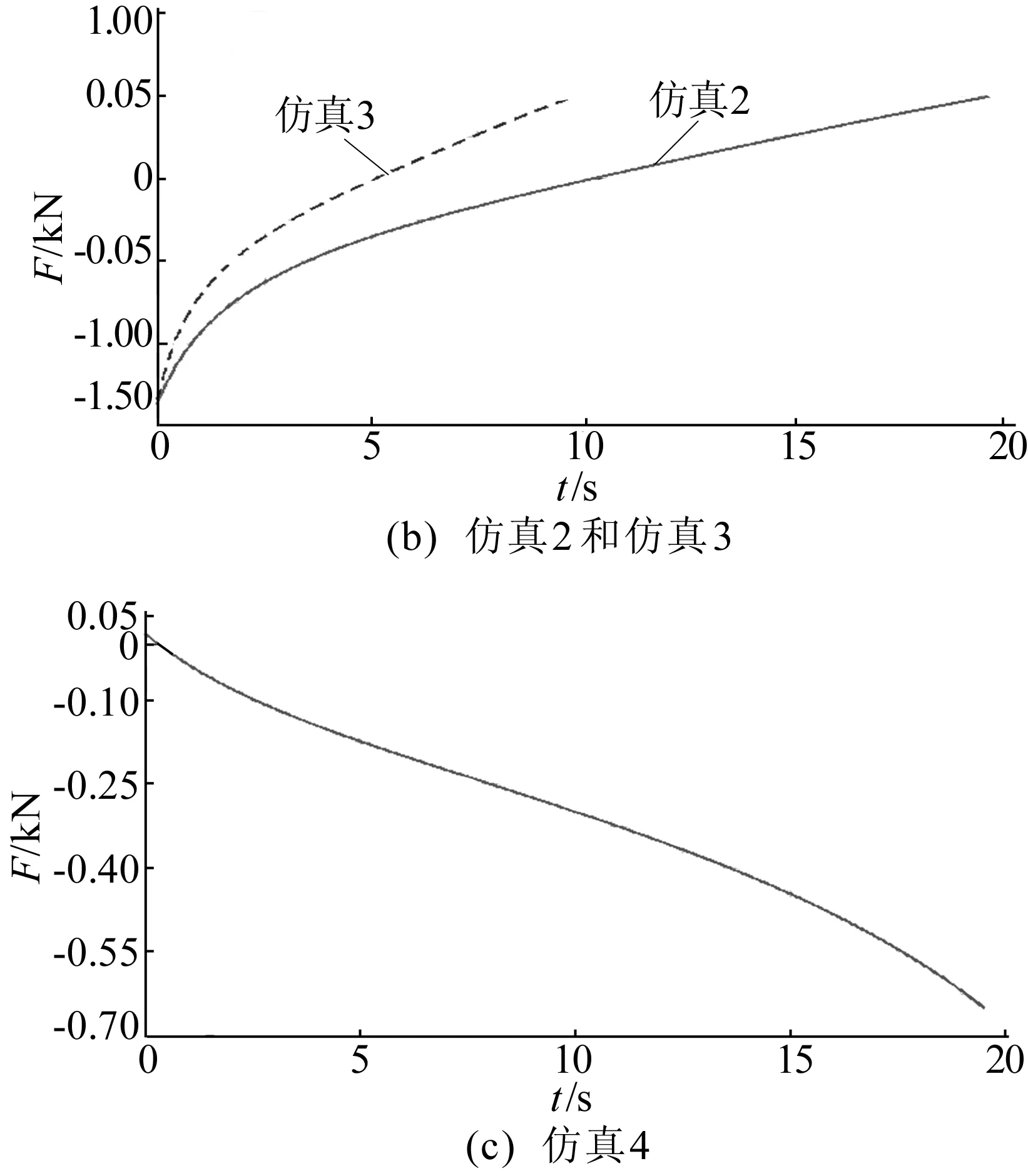
图3 平衡吊极限位置失衡力变化

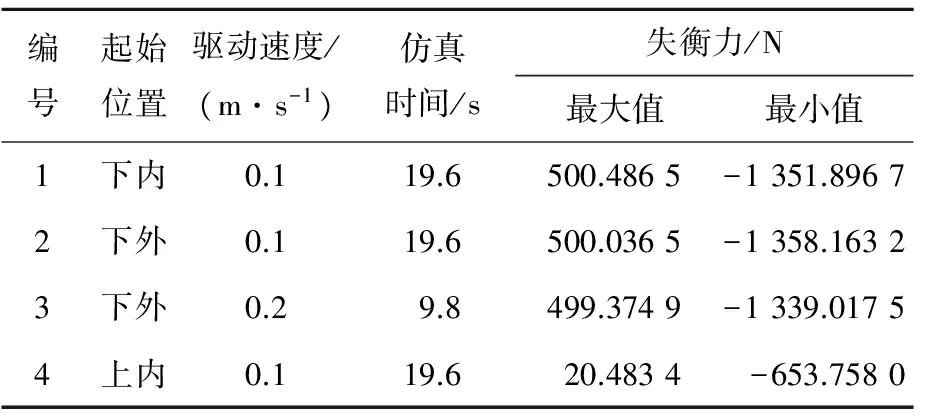
编号起始位置驱动速度/(m·s-1)仿真时间/s失衡力/N最大值最小值1下内0．119．6500．4865-1351．89672下外0．119．6500．0365-1358．16323下外0．29．8499．3749-1339．01754上内0．119．620．4834-653．7580

2.2 平衡吊失衡力分析

由于杆件自重是失衡力产生的直接原因,而由杆件自重引起的失衡力,其大小可通过理论力学推导得出[12]。

任意位置失衡力F大小的数学表达式为:

F=

其中,l为D、E两点间距离;h为A、B两点间距离;Gi(i=1,2,3,4)分别为DF杆、AD杆、BC杆、CE杆的重力;S1为DF杆上F点到其重心的距离;S2为AD杆上A点到其重心的距离;S3为BC杆上C点到其重心的距离;S4为CE杆上C点到其重心的距离;α为DF杆与水平方向夹角;β为AB杆与竖直方向夹角。

(2)式阐明了杆件重心在竖直方向的变化情况与失衡力大小存在相关关系。分析杆件重心位移可知其变化规律为先升高后下降。为实现降低失衡力的目的,提出如下改进方案:在不影响平衡吊正常工作的情况下,对其水平导轨进行适当变形,使其呈现两端高、中间低的外形。

在进行试验前,先对原模型进行力学分析,以得到结构优化的目标。运行仿真前需要为原模型销轴与水平导轨间的滑移副赋予一摩擦系数,考虑到各运动副运动状态及实际润滑情况,此处取0.001 5较为合适。对模型进行仿真,测定销轴与水平导轨间的摩擦力变化曲线,将曲线按照放大倍数m折算到起重臂末端F点,并将上文求得的失衡力绝对值放于同一图像内加以比较,结果如图4所示。其中,实线为失衡力变化趋势;虚线为等效摩擦力变化趋势,其变化较为平缓,位于下内位置时为198.576 4 N,移至下外位置时变为298.713 4 N。当失衡力大于摩擦力时会发生侧滑情况,破坏随遇平衡。因此,为保证随遇平衡,通过改进应使失衡力降至摩擦力曲线以下。

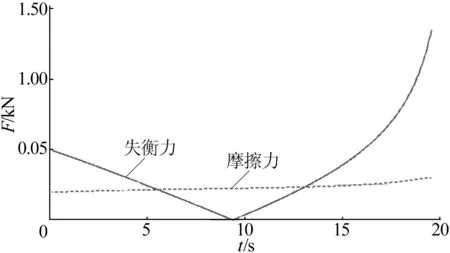
图4 失衡力与摩擦力的比较

3 平衡吊结构改进方案及效果验证

对总长392 mm的水平导轨进行改进,以原导轨内侧端点为坐标原点,导轨方向为x轴正方向,分别以(0,w)、(100,0)、(292,0)、(392,z)为坐标拟合出样条曲线并依此对导轨进行外形改进,使其呈现两端略高的形状,再以w-z形式命名各模型。在保持其他条件不变的情况下对各模型进行模拟仿真。各模型测得的失衡力示意图如图5所示，从上至下6组模型依次为5-5、10-10、15-15、20-20、20-30、20-35。

通过6组模型测得的失衡力数值及变化情况见表2所列。

通过表2可以得出如下结论:① 由前4组模型数据可知，水平导轨结构的改进对失衡力有着较大影响,且变形幅度越大,降低失衡力的效果也越明显;② 由20-20模型的数据可知位于下内位置时的失衡力已小于此位置的摩擦力,足以保证随遇平衡;而由于平衡吊的失衡力变化特性,杆件运行至下外位置时失衡力仍较大;③ 由20-35模型的数据可知,通过进一步提高导轨外端高度,失衡力变化的2个峰值均已降低至等效摩擦力以下,即实现了运行过程全程的随遇平衡。

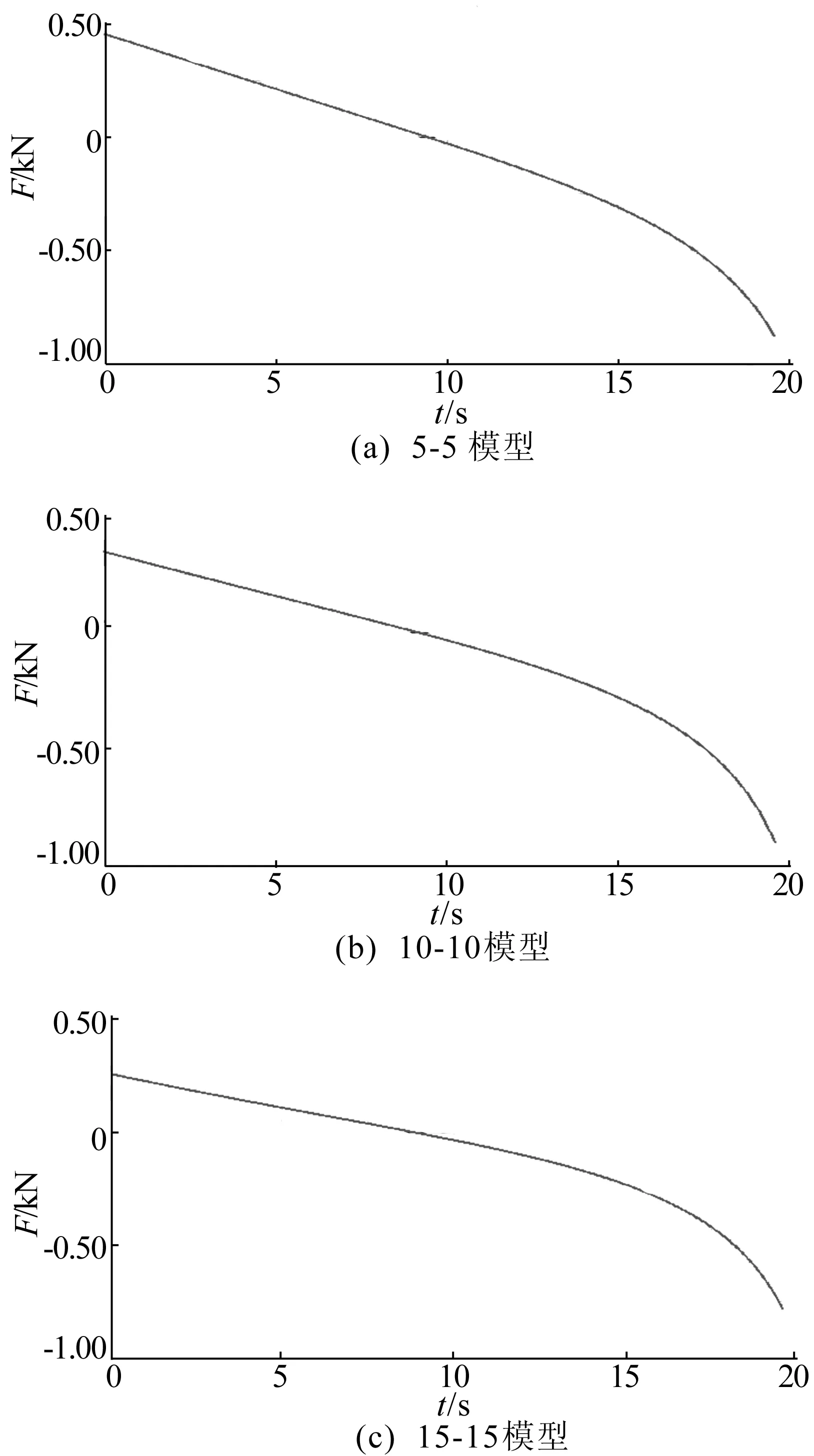
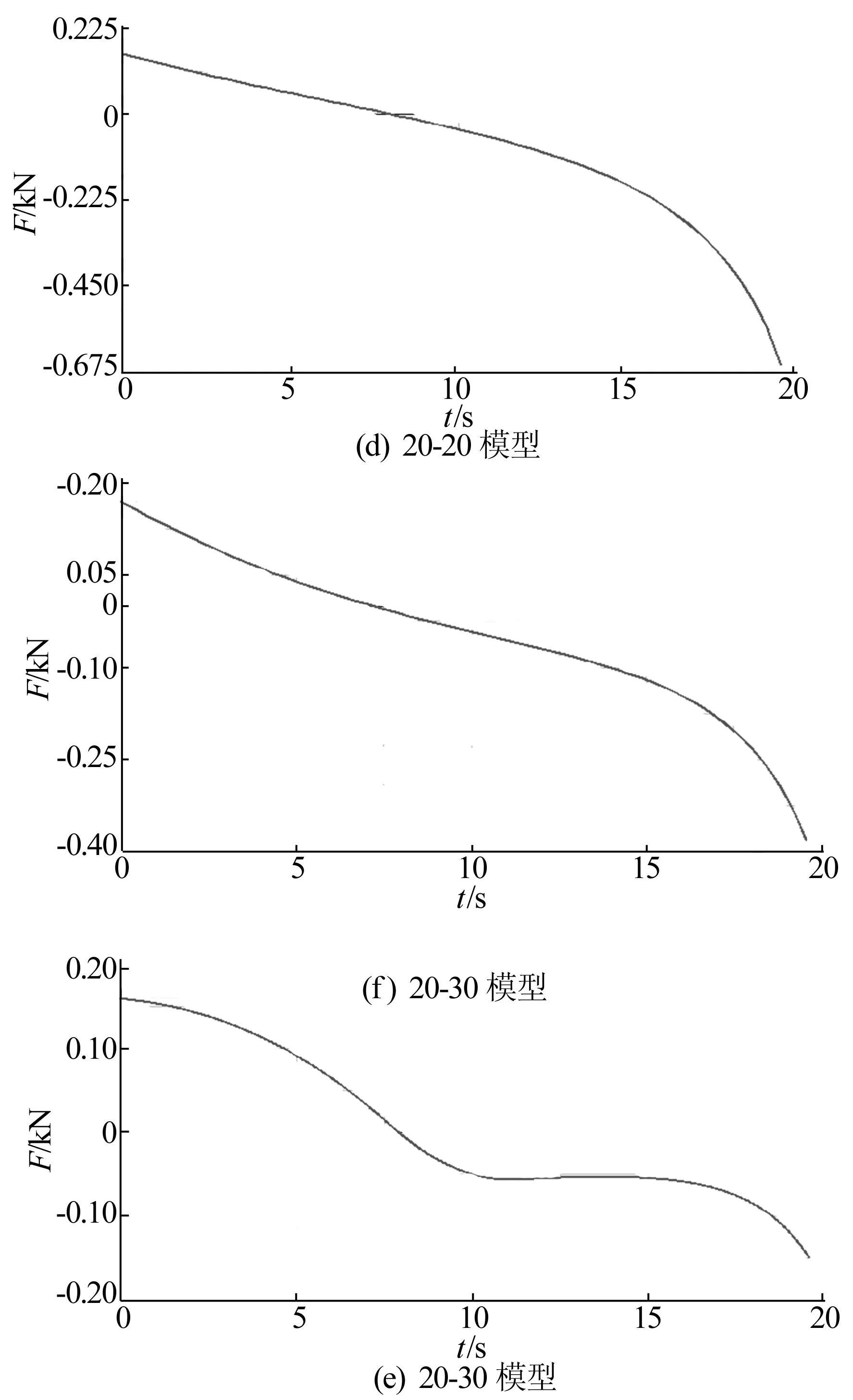
图5 各模型失衡力变化示意图

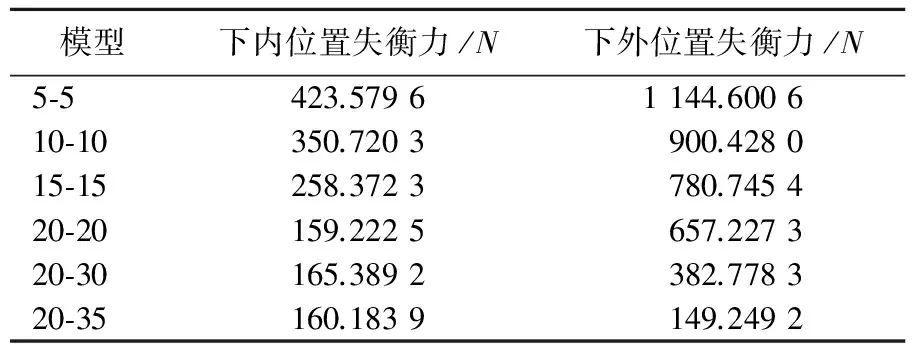
表2 改进后6组模型失衡力变化情况

4 结 论

本文以1 t电动平衡吊结构设计为基础,运用数字化建模及虚拟样机仿真的方法,得到了失衡力变化曲线;提出了在不增加自重的前提下通过改进水平导轨外形以降低失衡力的方法。对改进方法的仿真分析和效果验证可以证明,在电动平衡吊的设计过程中,该方法能够有效地降低失衡力对随遇平衡的不利影响,进而提高电动平衡吊工作效率及定位准确度,同时也为今后的平衡吊设计及改进工作提供一定的参考。

[1] 何全茂，何富贤.平行四连杆机构在平衡吊中的应用[J].煤矿机械，2011，31(10):196-197.

[2] 曹伟,郭伟,杨文珍.平衡吊切向和径向操作力的控制[J].装备制造技术,2011(2):144-149.

[3] 杨冲,陈坤.气动助力平衡吊设计及应用[J].中国机械，2013(2):103-104.

[4] CHENG X C，JIANG X W，CHENG Z X. Design and exploration on automobile counterweight balance [J]. Applied Mechanics and Materials，2014，457/458:1503-1506.

[5] 贺兵,刘扬,刘建华.基于ADAMS软件的啤酒瓶装箱机双四杆机构的运动仿真优化[J].轻工机械,2008,26(5):34-37.

[6] 汪奇谋,李华,姚进.基于ADAMS的变速箱传动系统的动力学仿真[J].机械传动,2013,37(6):75-77.

[7] 张晓帆,饶东杰,赵金涛.基于ADAMS的微车主减速器振动分析[J].合肥工业大学学报(自然科学版),2013,36(2):129-132,170.

[8] 陈晃,胡元洲,成相宜.基于MATLAB与ADAMS的四杆机构优化设计与仿真[J].中国机械,2014(13):201-202.

[9] 阚萍,石琴,祝安定.基于ADAMS的双横臂式前悬架K&C特性的仿真分析[J].合肥工业大学学报(自然科学版),2012,35(6): 732-735.

[10] 郑柳.机构放大倍数对平衡吊工作性能影响的分析与研究[J].装备制造技术,2010(9):50-52.

[11] 李增刚.ADAMS入门详解与实例[M].2版.北京:国防工业出版社,2014:67-87.

[12] 东南大学理论力学教研室.理论力学[M].3版.北京:高等教育出版社,2015:454-458.

Researchandsolutionsonout-of-balanceforceof1telectricbalancecranebasedonADAMSsoftware

ZHANG Yan, ZHANG Wenqiang

(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)

The out-of-balance force caused by self-weight of bars has an enormous adverse effect on neutral balance of balance crane. In this paper, digital models were built based on the design parameters of 1 t electric balance crane. And ADAMS software was used to research the influencing factors and trends of the out-of-balance force. An improvement scheme of changing the shape of horizontal guide rail was proposed to reduce the out-of-balance force. Remarkable extreme position was chosen to set up a series of models to test the proposed measure. The results show that the out-of-balance force can be reduced to a reasonable scope by changing the shape of horizontal guide rail properly, and then the neutral balance of balance crane can be guaranteed.

balance crane; neutral balance; out-of-balance force; horizontal guide rail; extreme position

2016-03-31；

2016-05-23

国家科技支撑计划资助项目(2012KJZC0789)

张 彦(1973-),女,山东临清人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.12.001

TH213.1

A

1003-5060(2017)12-1585-04

(责任编辑胡亚敏)