冲旋钻头结构对其寿命及破岩效率的影响研究

徐海良, 郑 义, 赵宏强, 徐绍军

(中南大学 机电工程学院,湖南 长沙 410083)

冲旋钻头结构对其寿命及破岩效率的影响研究

徐海良, 郑 义, 赵宏强, 徐绍军

(中南大学 机电工程学院,湖南 长沙 410083)

为研究气体冲旋钻头结构对其破岩性能的影响,文章采用非线性有限元分析软件ANSYS/LS-DYNA,以岩石力学和有限元理论为基础,选择适合岩石侵彻问题的Drucker-Prager本构模型,建立了气体冲旋钻头破岩的有限元模型,模拟不同结构气体冲旋钻头破岩的过程，得到了钻头破岩过程中力与时间的变化曲线以及平均力、比能随结构参数变化的曲线;当第2齿面倾角取25°、第3齿面倾角取44°、露齿高度取7.25 mm、钻齿半径取6.75 mm时,钻头所受的阻力平均值和钻头破岩所需比能较小,有利于延长气体冲旋钻头的使用寿命,并能提高能量利用率。

冲旋钻头;ANSYS/LS-DYNA软件;有限元;齿面倾角;载荷波动

为了解决硬质地层中非开挖扩孔的问题,设计了一种新型扩孔设备——反向扩孔气动冲击器[1]。该设备将冲击和旋转相结合进行破岩,活塞在高压气体的推动下快速周期运动,快速运动的活塞能够产生很大的冲击力,作用于钻头上,使得钻头与岩石的接触应力瞬时达到最大值,造成岩石较大的体积破碎,同时钻头在水平定向钻机带动下旋转切削岩石,实现冲击加旋转的破岩方式,极大地提高了碎岩效率[2-3]。但是由于对破岩机理的基础理论研究不足,导致缺乏较好地适用于该设备的钻具[4]。随着计算机技术的快速发展,采用计算机仿真技术对复杂的物理模型进行研究成为可能[5]。

文献[6]对冲旋钻头在单纯冲击载荷作用下的破岩效率进行了研究,但没有考虑钻头在冲击和旋转联合作用下所受的载荷;文献[7]研究了单个刀齿以不同的安装角及不同的钻进速度破岩时刀头的受力情况,但对钻头的露出高度、钻头大小没做相应的研究。在扩孔过程中,钻头的结构参数齿面倾角、露齿高度和钻齿半径会影响钻头的受力和比能。而钻头的受力和比能对钻头的使用寿命、能源利用率产生影响,进而决定了工程进度和成本。

因此，本文针对钻头的齿面倾角、露齿高度、钻齿半径展开研究,从而确定合适的钻头结构,以提高反向扩孔气动冲击器的整体性能。

1 钻头结构及工作原理

反向扩孔气动冲击器钻头结构如图1所示。钻头由刀体和嵌在刀体上的球齿组成,钻头前端分三级齿面,每个齿面上都嵌有球齿,以实现逐级扩孔的功能。钻头上设计了3条排气管道,不仅能排出冲击器内的尾气,而且能够为排屑流场提供入口气流。图1中钻头的关键参数有第2齿面倾角α(第2齿面与第1齿面的夹角)、第3齿面倾角β(第3齿面与第1齿面的夹角)、露齿高度h、钻齿半径r。

在工作过程中,第1齿面的齿尖最先与岩石接触,并将力作用于岩石的表面,由于作用力属于瞬时冲击动载荷,与刀齿接触的岩石瞬时就达到了其屈服极限,接触区域周围的岩石瞬间被压碎,形成破碎区,随着球齿钻入岩石,2个侧面的齿开始与岩石接触。在钻头的冲击力、摩擦力和切削力的共同作用下逐级扩孔。

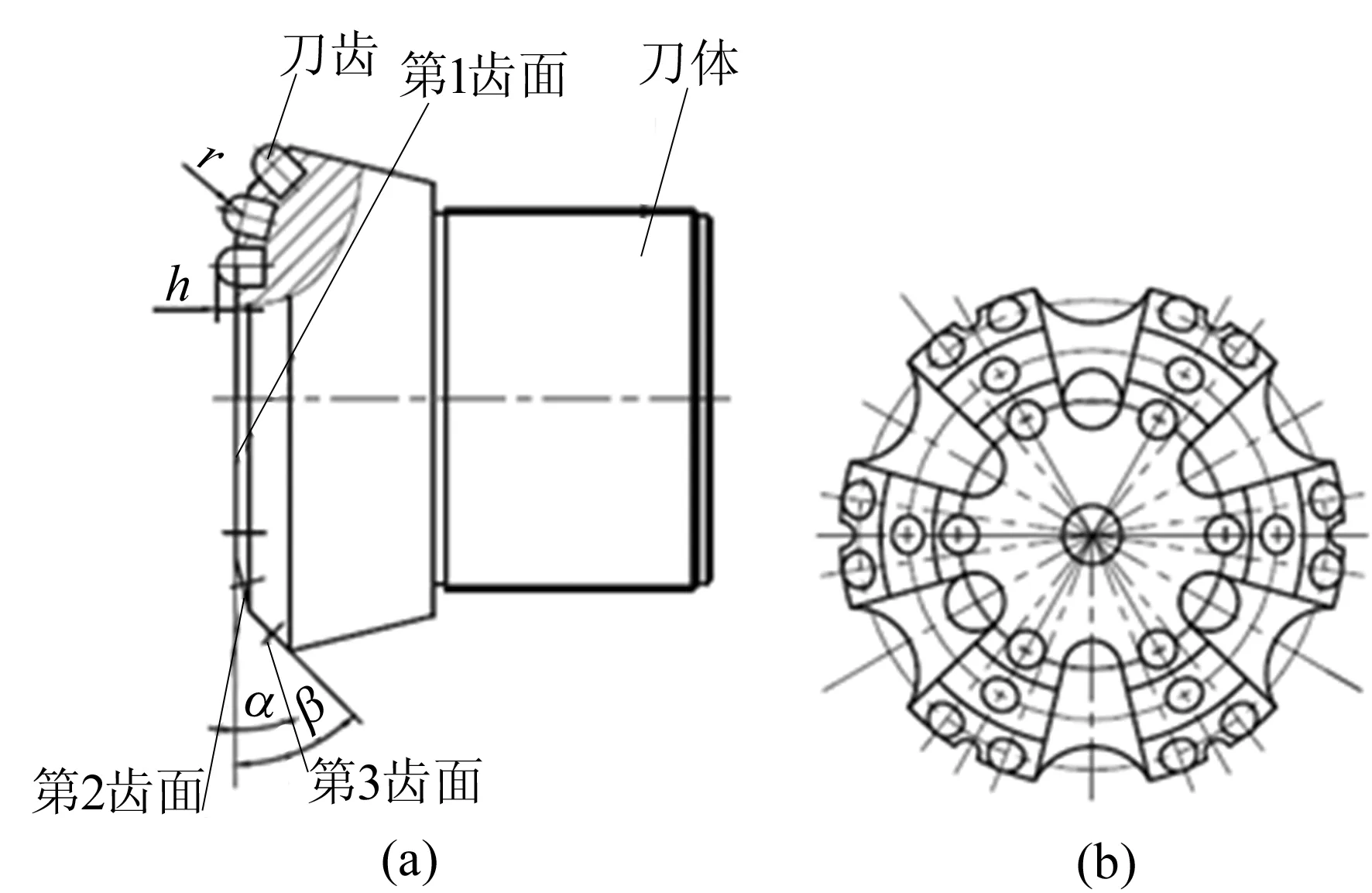
图1 冲旋钻头结构

2 钻齿的受力分析

冲旋钻头的钻齿由实心半球和圆柱组成,一部分通过过盈配合嵌入钻头,与钻头轴线的角度为钻齿倾角γ,球形钻齿的半径为r,露齿高度(整个牙齿高度减去嵌入钻头那部分高度)为h。球形钻齿对岩石的轴向载荷来源于冲击器活塞冲击钻头产生的冲击力[7],因此岩石对球形钻齿的轴向载荷方向向左,大小为P,钻齿破岩石时随着钻头转动,岩石对齿有水平载荷,方向垂直纸面向外,大小为F。球形钻齿与岩石互作用示意图如图2所示。

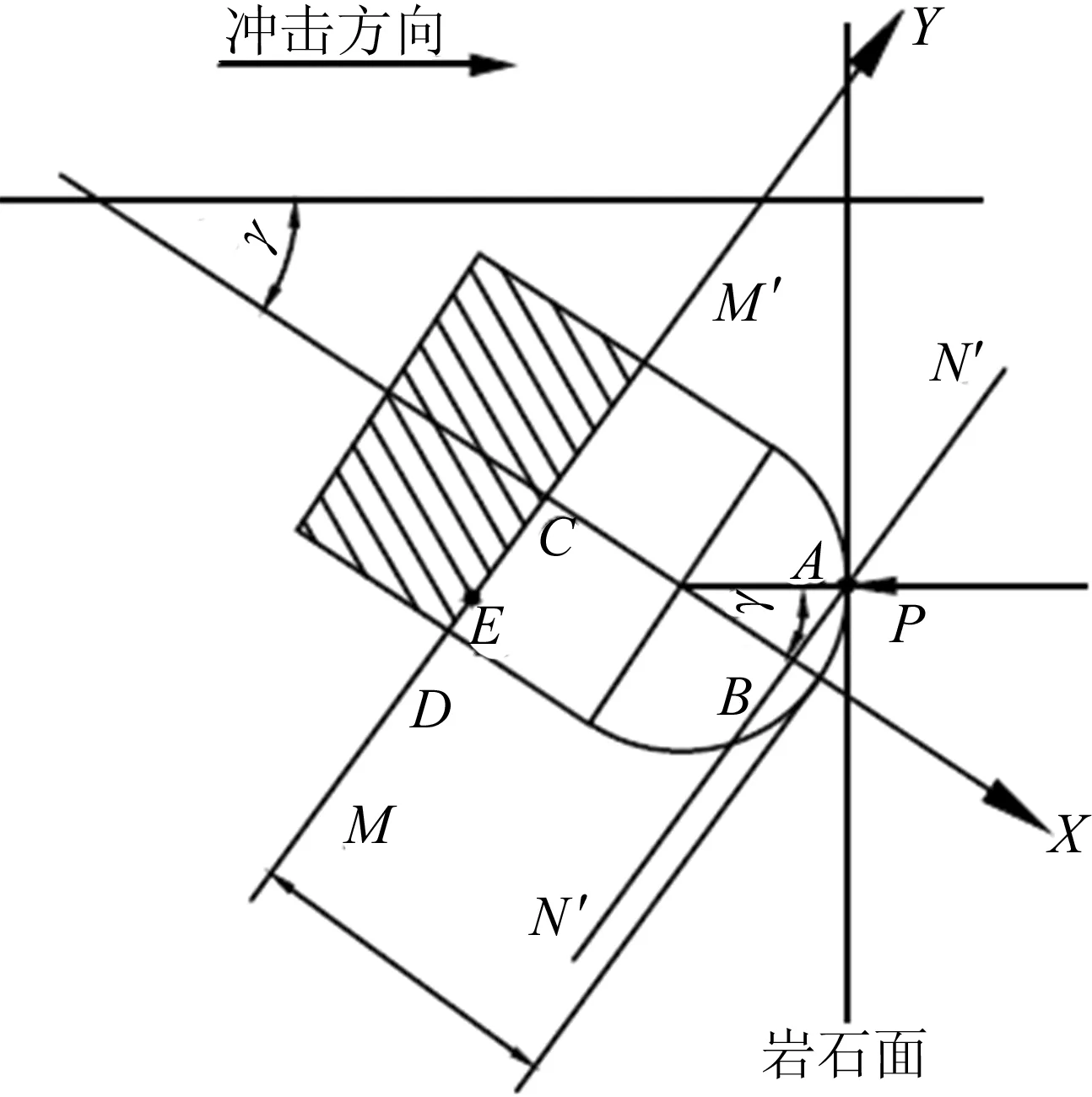
图2 球形钻齿与岩石相互作用示意图

3 建立仿真模型

3.1 三维实体模型的建立

在Pro/E中建立钻头及岩石的几何模型,岩石采用500mm×500mm×120mm的长方体。将模型导入HyperMesh中,在HyperMesh中对刀体、钻齿以及岩石分别采用自动划分网格,生成有限元模型,如图3所示。刀体、钻齿以及岩石均为实体模型,单元类型选取Solid164。应用单点高斯积分的单元,它能够较好地适用于大变形、材料失效以及接触等非线性问题。为了避免产生沙漏问题,采用总体附加刚度，使总体砂漏不超过模型总体内能的10%[8]。

图3 钻头和岩石的有限元模型

3.2 模型材料的定义

本文中刀齿材料采用YG15硬质合金,因为钻头的强度和硬度远大于岩石的强度和硬度,破岩过程中钻头形变量非常小,且仿真过程的目的在于分析钻头的受力,而不是钻头的变形,所以将钻齿和钻头都视作刚体,以缩短计算时间。用*CONSTRAINED-RIGID-BODIES将2个刚体连接起来,并对钻头的X、Y位移约束和X、Y、Z转动进行约束[9]。

本文岩石采用线性Drucker-Prager模型,它能够反映岩石的基本特性,将相应的参数设置作为岩石的材料参数,用于模拟岩石材料本构。相应的材料参数见表1所列。添加失效模型MAT-ADD-EROSION,控制主应力为20MPa来模拟裂纹的扩展,即认为当岩石受到的主应力超过材料失效准则所设定的主应力之后,单元失效删除。

表1 材料参数

3.3 定义接触、边界条件及载荷、求解时间

3.3.1 定义接触

在K文件中添加*CONTACT-ERODING-SURFACE-TO-SURFACE,即将钻齿和岩石之间的接触类型定义为面对面的侵蚀接触,来模拟钻头破碎岩石过程。

3.3.2 定义边界条件及载荷

将岩石的底面全约束,限制岩石的移动和转动。为了避免在岩石模型的边界产生的人工应力波反射重新进入模型从而破坏结果,设定岩石模型外表面为非反射边界条件,以模拟无限域。

为了实现钻头的旋转和进给2种运动,定义钻头的旋转速度n=150r/min和钻进18mm,并限制其他4个自由度。

3.3.3 求解控制设置

为了充分模拟钻头在破岩过程中的受力状况,添加关键字*CONTROL-TERMINATION,并设置求解时间为0.4s。

4 气体冲旋钻头结构参数的分析

在破岩过程中,钻头所受的平均阻力大小以及比能是判断钻头结构优劣的依据。比能是指破碎单位体积岩石所消耗能量,该值越小,说明所需的能量越小,钻头结构越合理[10-11]。由于本文采用体积相等的单元划分岩石,单元数目间接反映了体积的大小。为了便于计算,将破碎删除单位个数的单元所需能量记为We,其值越小,说明所需的能量越小,钻头结构越合理。下面对钻头破岩的主要影响因素逐一进行分析。

4.1 第2齿面倾角α

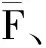
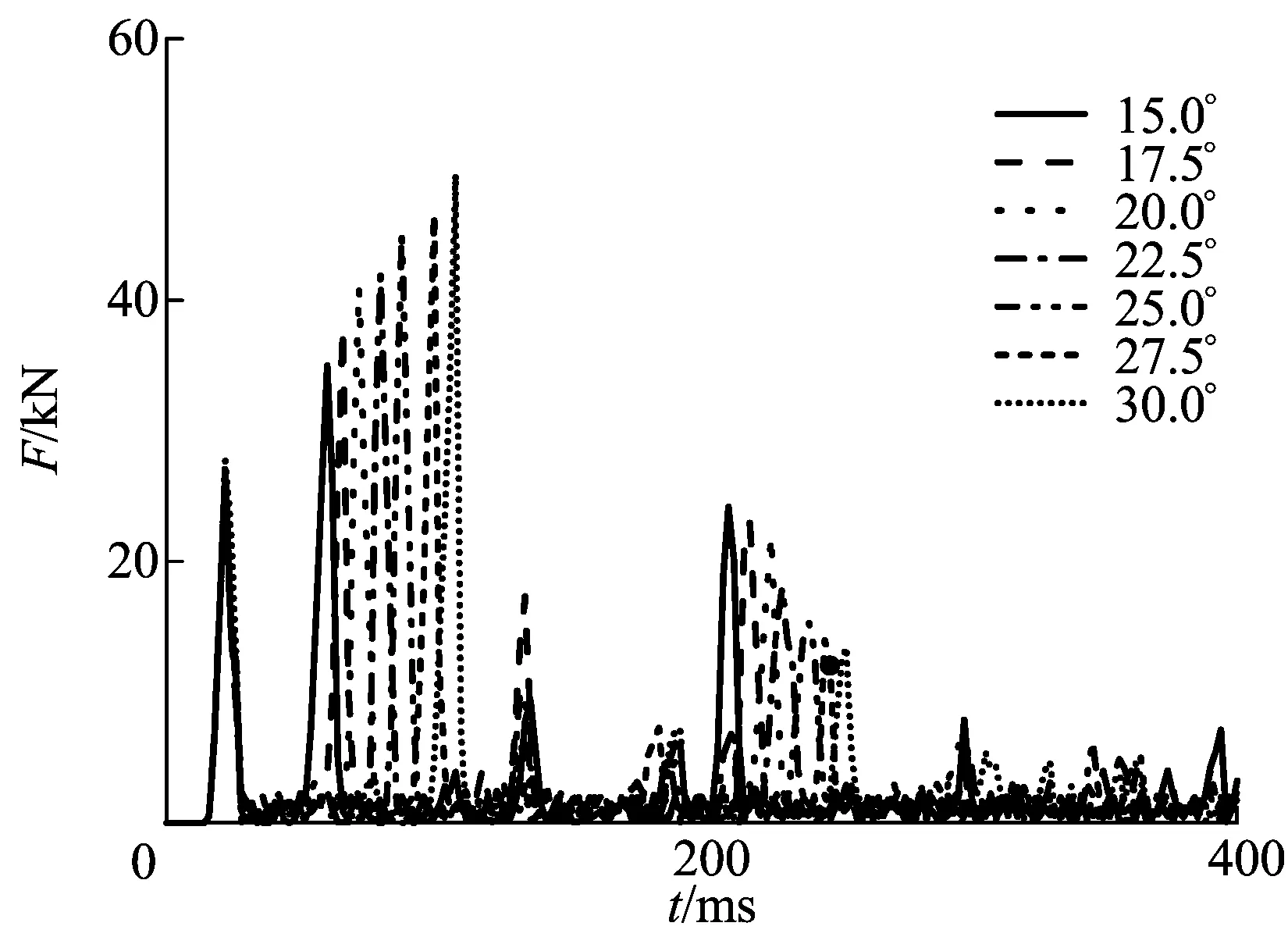
图4 α不同时阻力随时间变化的曲线

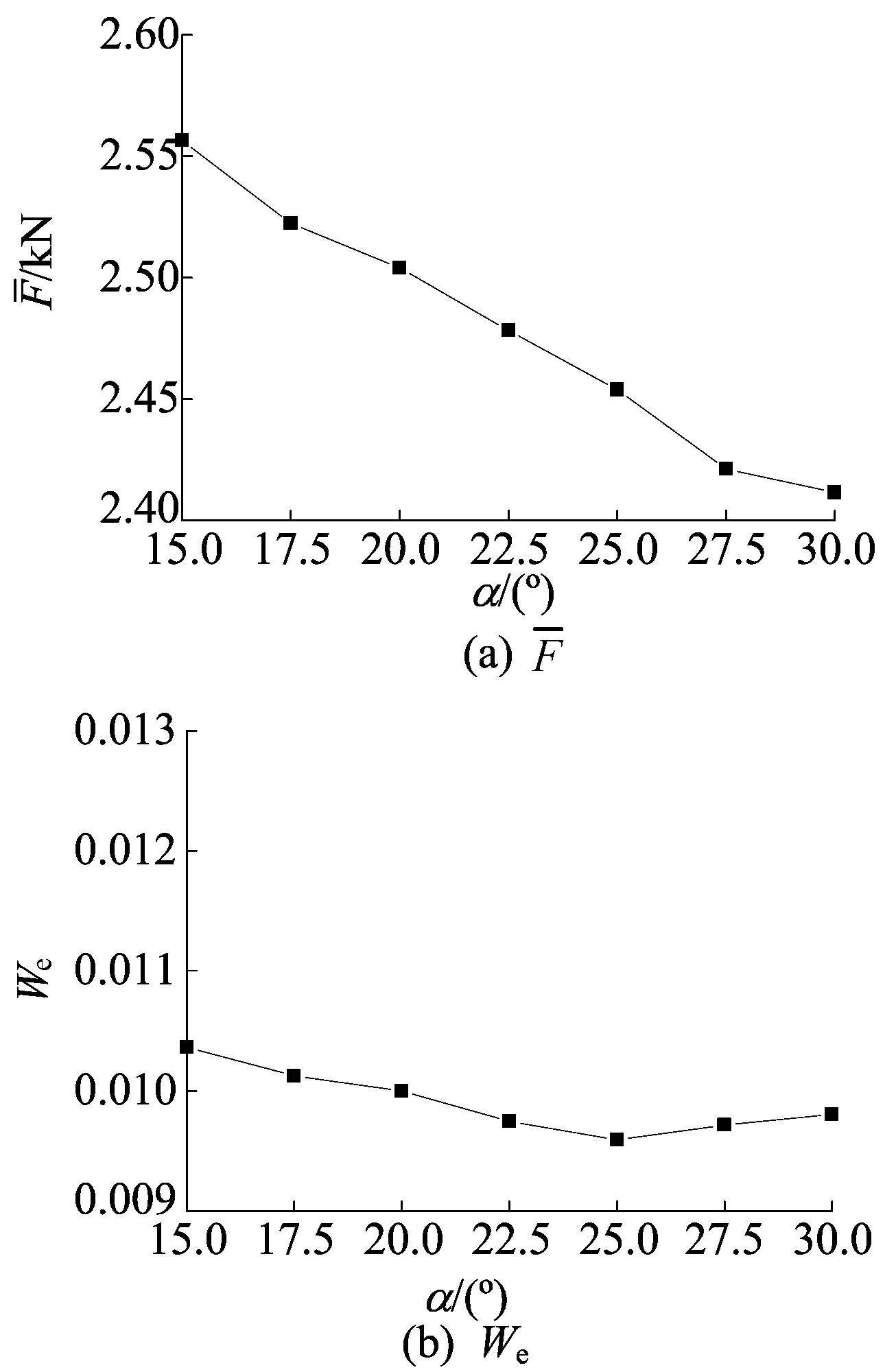
图5 平均阻力和比能随第2齿面倾角变化的曲线

由图4和图5可知,随着第2齿面倾角的增加,第2个主波峰数值增大,出现的时间越来越靠后；第3个主波峰数值变小，出现的时间也越来越靠后。这是由于随着第2齿面倾角的增加,齿面上的钻齿与岩石的相对位置越来越靠后。钻头所受平均阻力随着第2齿面倾角的增加逐渐减小。当α=25°时,钻头破岩所需要的比能耗最低。

4.2 第3齿面倾角β

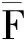
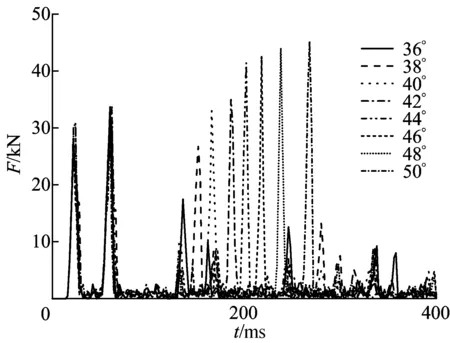
图6 β不同时阻力随时间变化的曲线

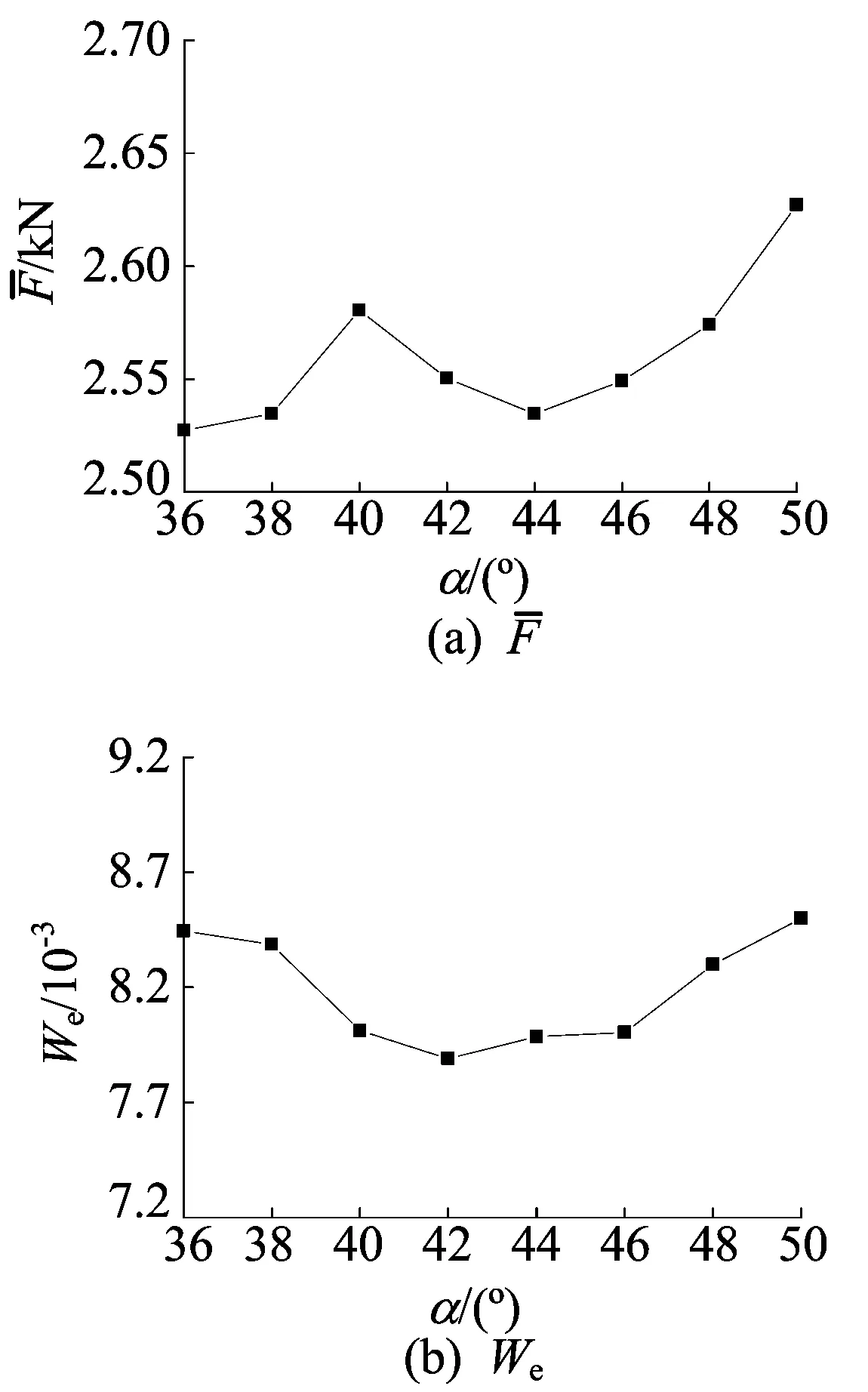
图7 平均阻力和比能随第3齿面倾角变化的曲线

由图6、图7可知,由于第1齿面、第2齿面倾角不发生变化,因此前2个主波峰出现的时间基本一致,钻头所受阻力基本相等。随着第3齿面倾角的增加,齿面上的钻齿与岩石的相对位置越来越靠后,第3个主波峰出现的时间也越来越靠后,且阻力的最大值不断增加。当β为36°、38°、44°时,钻头所受阻力较小,使用寿命增加；当β为42°、44°时,钻头破岩所需要的比能耗低。因此，在其他参数不变的情况下,第3齿面倾角取44°比较好。

4.3 露齿高度h

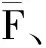
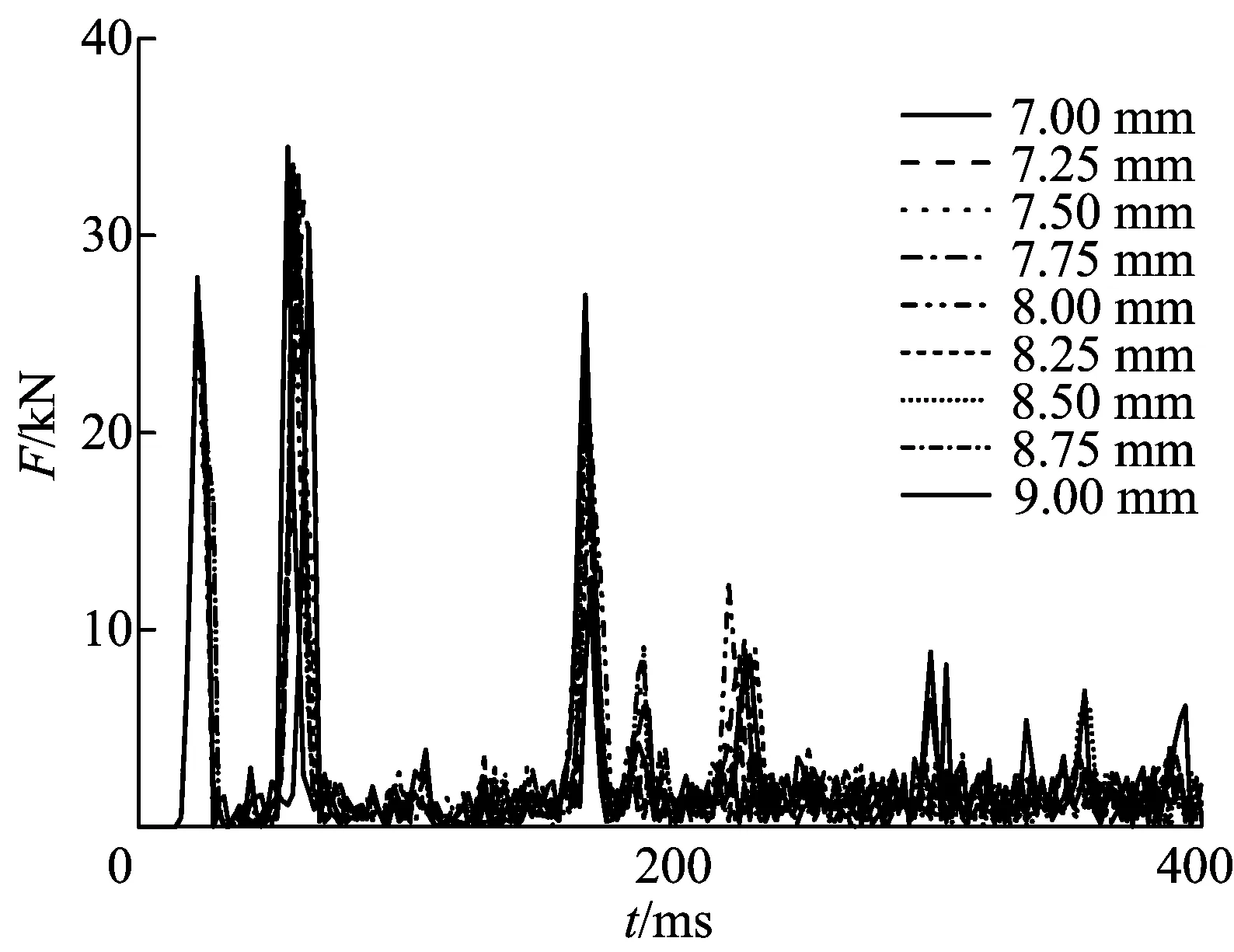
图8 h不同时阻力随时间变化的曲线

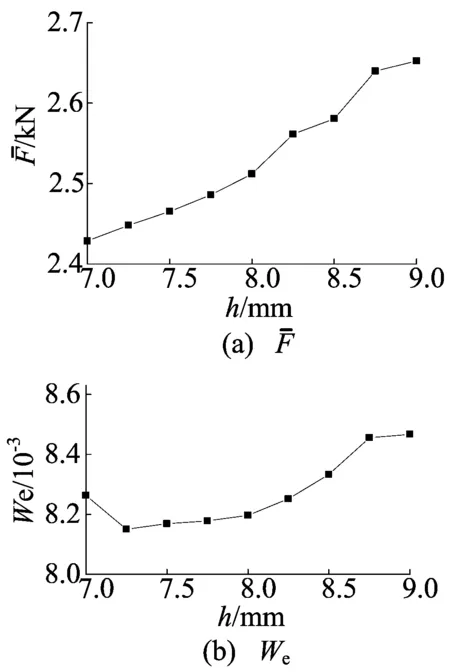
图9 平均阻力和比能随露齿高度变化的曲线

由图8、图9可知,3个主波峰出现的时间点会随着露齿高度的增加,而向前移动,但幅度不大。这是由于在同样的齿面倾角下,露齿高度越高,钻头与岩石接触的时间越早,钻齿与岩石的接触面积增加,引起破岩量的增多以及阻力的增大。钻头所受的平均阻力随着露齿高度的增加而增加。当h=7.25mm时,钻头破岩时单位体积所需要的比能耗最低。

4.4 钻齿半径r

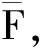
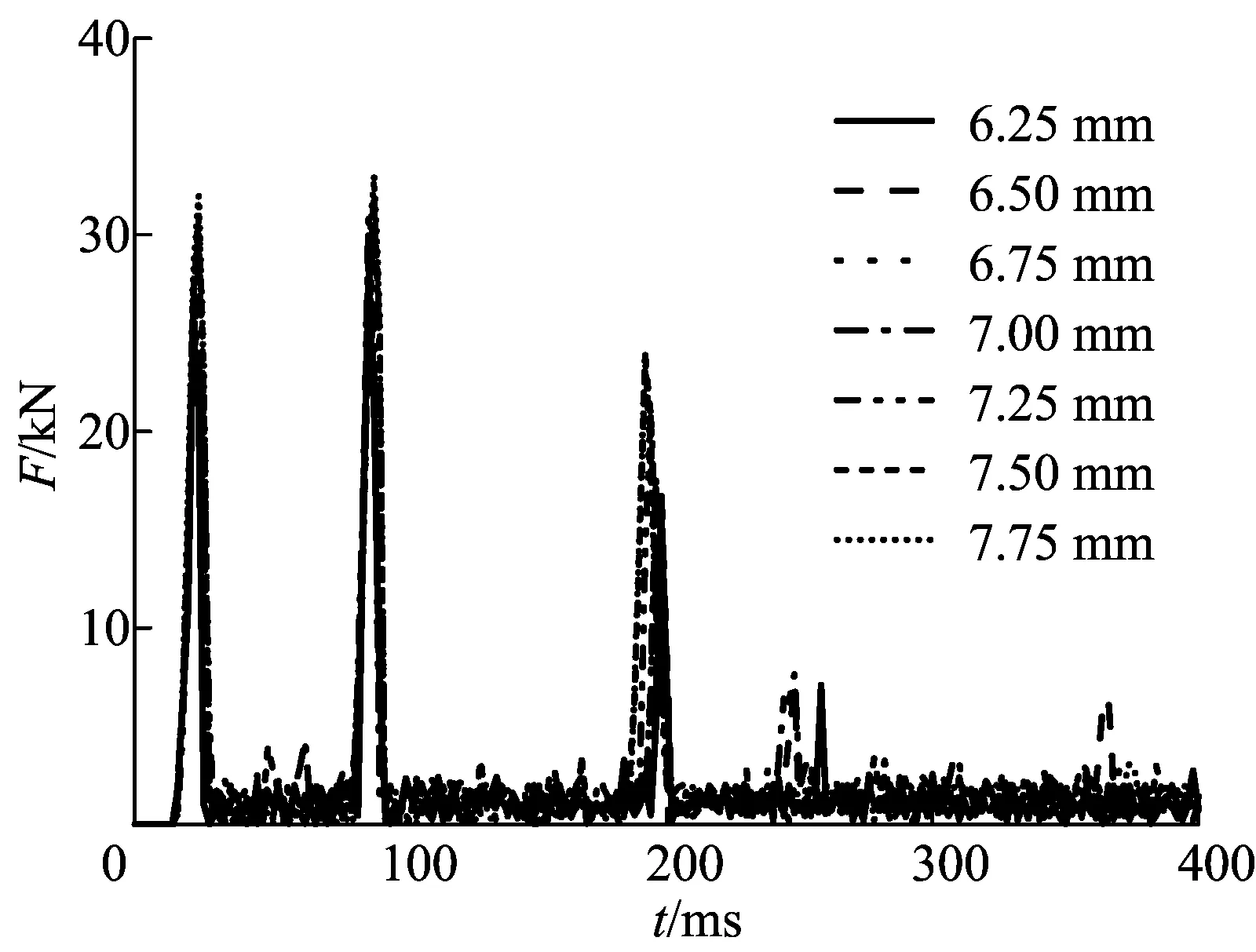
图10 r不同时阻力随时间变化的曲线

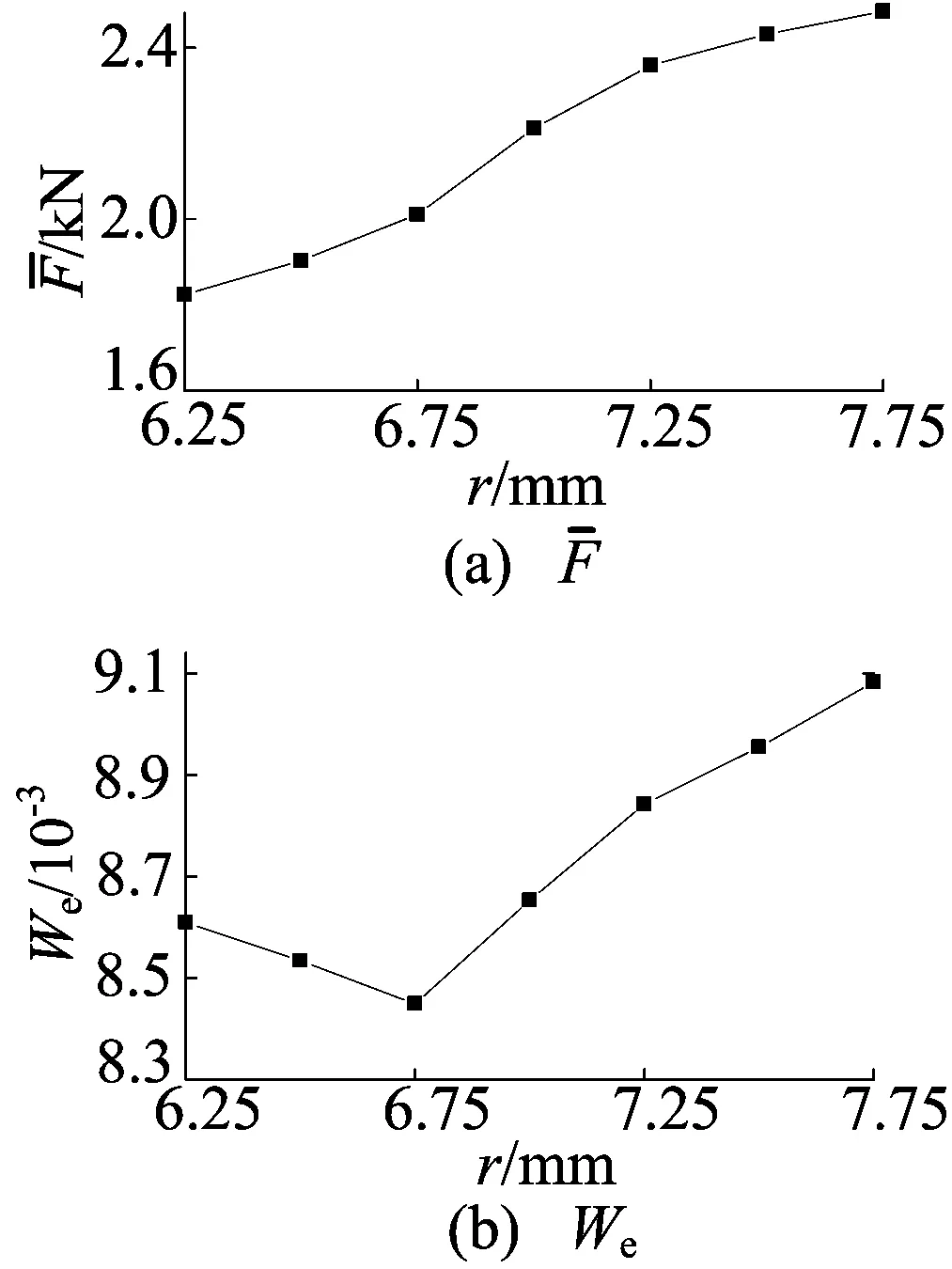
图11 平均阻力及比能随钻齿半径变化的曲线

由图10、图11可知,3个主波峰出现的时间点会随着钻齿半径的增加而向前移动,但幅度不大。这是由于在同样的齿面倾角下,钻齿半径越大,钻头与岩石接触的时间越早。同时由于钻齿半径增大,钻齿与岩石的接触面积增加,引起破岩量的增多以及阻力的增大。钻头所受的平均阻力随着钻齿半径的增加而增加。当r=6.75mm时,钻头破岩时单位体积所需要的比能耗最低。

5 结 论

本文利用LS-DYNA对钻头扩孔过程进行了模拟,通过对仿真结果分析得出如下结论:

(1) 在其他参数不变的情况下,第2齿面倾角取25°时,钻头所受的阻力平均值较小,有利于延长钻头使用寿命,同时钻头破岩的比能达到最小。

(2) 第3齿面倾角取44°时,不仅扩孔效率较高,而且钻头所受平均阻力小,此种结构有利于延长钻头的使用寿命。

(3) 露齿高度h=7.25mm时,钻头所受平均阻力最小,同时比能低。

(4) 钻齿半径r=6.75mm时,钻头破岩时单位体积所需要的能耗最低,平均阻力小。

本文得到的结构参数与切削力及比能的变化关系可以用于指导钻头结构参数的合理选择,最终实现钻头的优化设计。

[1] 徐绍军,徐大鹏,徐海良,等.气动回扩锤的计算机仿真与优化研究[J].工程机械,2008,39(1):16-19.

[2] 呼咏.钻头自回转型潜孔锤研究及仿真分析[D].长春:吉林大学,2007.

[3] AN B,TANNANT D.Discrete element method contact model for dynamic simulation of inelastic rock impact[J].Computers & Geosciences,2007,33(4):513-521.

[4] 谭力,徐延金,黄志强,等.气动冲旋钻头破岩过程仿真研究[J].西部探矿工程,2008,20(4):69-71.

[5] 梅顺齐.现代设计方法[M].武汉:华中科技大学出版社,2009.

[6] 黄志强,范永涛,魏振强,等.冲旋钻头破岩机理仿真研究[J].西南石油大学学报(自然科学版),2010,32(1):148-150.

[7] 张艳林,闫炳雷,陈锷,等.基于ANSYS/LS-DYNA的掘进机截齿截割煤岩动力学分析[J].机械设计,2013,30(2):74-77.

[8] 林元华,李润方,施太和,等.空气冲旋钻井机械钻速仿真算法[J].重庆大学学报(自然科学版),2004,27(8):1-6.

[9] 黄志强,谭力,金鑫,等.基于LS-DYNA的冲旋钻头牙齿破岩机理仿真研究[J].天然气工业,2007,27(4):76-78.

[10] 闫铁,李玮,毕雪亮,等.一种基于破碎比功的岩石破碎效率评价新方法[J].石油学报,2009,30(2):291-294.

[11] 李玮,闫铁.基于分形岩石破碎比功方程的钻井优化[J].石油学报,2011,32(4):693-696.

Effectofstructureofpercussion-rotarybitonitsservicelifeandrockbreakingperformance

XU Hailiang, ZHENG Yi, ZHAO Hongqiang, XU Shaojun

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

In order to study the effect of the structure of air percussion-rotary bit on its rock breaking performance, the nonlinear finite element software ANSYS/LS-DYNA was adopted. According to rock mechanics and finite element theory, a Drucker-Prager constitutive model was selected for penetration problems of rock, and the finite element model of air percussion-rotary bit was then established to simulate the process of rock breaking by air percussion-rotary bits with different structures. The curves of resultant force varying with time, the relation curves of average resultant force and specific energy varying with structure parameters were gotten. When the second and the third tooth surface angle of the air percussion-rotary bit, the height and radius of the teeth of the air percussion-rotary bit was 25°, 44°, 7.25 mm and 6.75 mm， respectively, the average resultant force and specific energy were relatively smaller. This can help to prolong the service life of the air percussion-rotary bit and to improve energy utilization.

percussion-rotary bit; ANSYS/LS-DYNA; finite element; angle of tooth surface; load fluctuation

2016-07-19；

2016-02-13

国家自然科学基金资助项目(51375499)

徐海良(1965-),男,湖南湘乡人,博士,中南大学教授,博士生导师;

徐绍军(1965-),女,湖南沅江人,博士,中南大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.12.004

TH47

A

1003-5060(2017)12-1599-05

(责任编辑胡亚敏)