分数槽Halbach永磁直线同步电机磁场解析计算

师宇飞, 汪旭东, 许孝卓, 封海潮

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

分数槽Halbach永磁直线同步电机磁场解析计算

师宇飞, 汪旭东, 许孝卓, 封海潮

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

分数槽Halbach永磁直线同步电机(fractional-slot Halbach permanent magnet linear synchronous motor,FH-PMLSM)的次级永磁体采用Halbach阵列,初级绕组采用端部不重叠的集中绕组,与常规的分数槽永磁同步直线电机相比,具有推力密度大、损耗小等优点,适用于长行程、大推力驱动场合。文章在Halbach永磁阵列的电流密度等效基础上,对16极15槽FH-PMLSM建立分层解析模型,利用矢量磁位和边界条件推导出气隙区域、齿槽和永磁体区域磁场的解析公式,并结合分布式卡式系数分析FH-PMLSM励磁磁场的分布,进一步对不同气隙长度的FH-PMLSM的电磁推力进行计算。结果表明:解析计算与有限元计算的磁场结果基本吻合,验证了该解析方法的正确性,为分数槽Halbach永磁同步直线电机的工程分析和优化设计提供了依据。

Halbach永磁直线同步电机;分层解析模型;分数槽集中绕组;分布卡式系数;磁场计算

在垂直提升系统领域内,永磁直线同步电机(permanent magnet linear synchronous motors,PMLSM)以其结构简单、力能指标高、动态性能好、功率密度高等优点[1],被公认为是最理想的驱动源之一。尤其是分数槽集中绕组的永磁直线同步电机,具有端部绕组短、铜耗小、推力波动小、安装成本低等显著优势[2]。但是,与整数槽分布绕组的永磁直线同步电机相比,其推力密度下降。这样就减小了提升系统的推力自重比,降低了提升系统性能。而次级采用Halbach磁体结构的永磁直线同步电机,比常规的磁体结构,推力密度得到了提高[3]。本文研究的分数槽Halbach永磁直线同步电机(fractional-slot Halbach permanent magnet linear synchronous motor,FH-PMLSM,FH-PMLSM)在具有分数槽永磁直线同步电机优点的同时,弥补了分数槽直线电机推力小的劣势,在垂直提升系统中具有更高的应用价值。

目前,国内外对分数槽Halbach永磁直线同步电机的研究很少,大部分是关于无铁心Halbach型永磁直线电机的研究。文献[4]对比分析了径向永磁阵列结构和Halbach阵列结构的2种无铁心绕组的直线电机,通过空载反电动势、静态推力和闭环定位实验说明了Halbach阵列较径向永磁阵列的优点;文献[5]提出并分析了一种新型Halbach阵列的无铁心永磁直线电机;文献[6]将一种梯形型式的绕组应用到无铁心Halbach永磁直线电机中,并建立解析模型,进而分析了推力波动等问题。近年来,分数槽集中绕组技术以其特别的优势引起国内外学者的广泛关注[7]。文献[8]研究了分数槽低速永磁风力发电机的电磁设计和性能优化等问题;文献[9]通过不同极槽配合的电机绕组排列方式,推导出分数槽集中绕组电机电枢反应磁场的公式,通过相对磁导函数计及开槽对电枢反应磁场的影响,并以此为基础分析了磁场的各次谐波含量。

本文在合理假设的前提下,建立分数槽Halbach永磁直线同步电机的分层解析模型,对Halbach永磁体进行等效,运用傅式级数法推导出电机不同区域下磁场的解析公式,考虑齿槽效应的影响,应用分布式卡式系数改进磁场计算精度,解析求解不同气隙下电机的推力,通过有限元结果验证所提方法的正确性。

1 电机分析模型

分数槽Halbach永磁直线同步电机的物理模型如图1所示。Halbach阵列每极下具有2块永磁体,充磁方式分别为水平充磁和竖直充磁。为简化分析,本文做如下假设:① 磁场沿z轴方向无变化,因此电机磁场可按照二维场进行近似求解；② 次级背铁和初级铁轭的磁导率为无穷大；③ 永磁体均匀磁化,其磁导率等于空气磁导率；④ 忽略铁芯饱和的影响；⑤ 忽略槽口对磁场分布的影响；⑥ 电机齿槽区域等效为x、y方向磁导率不同的均匀线性区,且x、y方向的相对磁导率[10]分别为:

μy=μ0[2bs/ts+μr(1-2bs/ts)]

(2)

其中,μ0为空气磁导率;μr为铁心相对磁导率;bs为虚槽宽；ts=bt+2bs为槽距，bt为齿宽。在上述假设的基础上建立分数槽Halbach永磁直线同步电机磁场的分层解析模型,如图2所示。图2中，g为气隙长度；hm为永磁体厚度；hs为槽深。

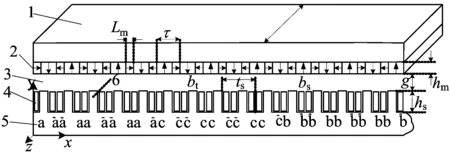
1.次级轭 2.Halbach永磁阵列 3.气隙 4.槽绕组 5.初级轭 6.齿图1 电机分析物理模型

图2 电机磁场分层解析模型

2 永磁体等效电流密度分布

虽然本文提出的分数槽Halbach永磁直线同步电机(FH-PMLSM)与分数槽集中绕组永磁直线同步电机(FW-PMLSM)的初级结构和电枢绕组布置方式一致,但次级的磁体结构不同,其中FW-PMLSM的次级下均为竖直充磁的永磁体,而FH-PMLSM 的次级不仅有竖直充磁的永磁体,还有水平充磁的永磁体,FW-PMLSM的永磁体等效处理方法不能适用于FH-PMLSM的永磁磁场分析,因此,本文对Halbach永磁阵列进行等效,提出适用于FH-PMLSM永磁磁场的分析方法。本文对永磁体磁场的分析采用等效磁化强度法,将Halbach阵列中的永磁体作为“统一的整体”等效为上、下2个无限薄的面电流层和位于两者之间的体电流,Halbach阵列中永磁体的等效磁化强度空间分布函数为:

M=Mxi+Myj

(3)

其中,Mx为永磁体沿x方向磁化的磁化强度分量;My为永磁体沿y方向磁化的磁化强度分量,其表达式为:

其中,n为计算谐波次数;τe为电机x方向有效长度;β=π/τe。

永磁体等效面电流层电流密度分布可以表示为:

采用傅立叶级数展开上式,可得:

其中,p为电机极对数;Hc为永磁体矫顽力。

永磁体等效体电流密度分布表示为:

采用傅立叶级数展开(7)式,可得:

3 磁场计算和修正

3.1 永磁磁场计算

为简化磁场计算推导过程,首先定义以下函数:

f1(r,a,b)=coshacoshb+rsinhasinhb

(9)

f2(r,a,b)=coshasinhb+rsinhacoshb

(10)

标量磁位方程如下:

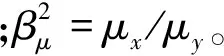
Hp1x|y=0=0,

Hp3x|y=hs+g+hm=Jzp(x),

Bp1y|y=hs=Bp2y|y=hs,

Hp1x|y=hs=Hp2x|y=hs,

Bp3y|y=hs+g=Bp2y|y=hs+g,

Hp3x|y=hs+g=Hp2x|y=hs+g+Jzp(x)

(12)

通过分离变量法求解(11)式、(12)式,得到Halbach永磁体作用下磁场的解析公式。

齿槽区域磁场为:

Bp1y(x,y)=

其中,R=βμμ0/μx；V=nββμ；L=g+hm；α=(1-coshnβhm)Mxpn+(sinhnβhm)Mypn。

气隙区域磁场为:

Bp2y(x,y)=

coshnβy+f2(R,Vhs,-nβhs)sinhnβy]

(14)

Halbach永磁体区域磁场为:

Wsinhnβy)cosnβx

(15)

其中

Mxpnsinhnβhg-Mypncoshnβhg;

Mxpncoshnβhg+Mypnsinhnβhg；hg=g+hs。

3.2 电枢反应磁场

在上述的磁场分析计算中,虽然未涉及到电枢绕组单独作用下的磁场求解。但是对于电机的初级结构和电枢绕组布置方式,本文研究的分数槽Halbach永磁直线同步电机与文献[11]研究的电机基本一致。因此电枢反应气隙磁密的解析计算公式可以引用文献[11]中相应的公式,这里不再赘述。公式如下:

coshnβ(y-hp)cosnβx

(16)

其中

hp=hm+g+hs。

3.3 计及齿槽效应的修正系数

针对分数槽永磁直线同步电机磁场解析计算的情况,传统卡式系数法在磁密波峰处会出现明显的误差,而分布式卡式系数法能计及铁心开槽对磁场分布的影响,使误差能够降到满足工程分析需要的范围内[11]。因此,本文采用分布式卡式系数对磁场解析计算的结果进行修正。

传统的卡式系数法实际上是将有槽电机等效为一台气隙长度为Kcg的无槽电机,其中Kc为依据许克变换得出的等效气隙系数[11],即

其中

分布式卡式系数K(x)公式[12]如下:

其中

Kn=(Kc-1)[sinnk(bt+bs)-sinnkbs]/nπ；

k=2π/ts。

计及齿槽效应下的磁密分布B′(x,y)为:

B′(x,y)=K(x)B(x,y)

(19)

其中,B(x,y)为等效无槽电机的磁密分布。

4 有限元结果验证

为验证上述分析方法的正确性,本文运用Magnet有限元软件对一台16极15槽电机进行建模仿真,计算得到电机气隙磁密分布结果,并与解析结果进行对比验证。电机参数见表1所列。

表1 电机参数

电机气隙磁密解析计算结果与有限元计算结果的对比情况如图4所示。

图3 电机气隙磁密分布

由图4可知，解析法与有限元法得到的气隙磁密波形基本吻合，分布式卡式系数修正后的解析结果很好地反映了铁心开槽对磁场分布的影响,验证了本文所提解析方法的合理性。

5 电磁推力分析

电机的电磁推力计算公式为:

其中,S为齿槽区域面积;Lw为电枢有效长度;Jw(x,y)为电枢绕组等效体电流密度函数[12]。

在相同电枢电流的前提下,采用解析法分别对不同气隙长度的FH-PMLSM电磁推力进行计算,并与有限元法计算的结果进行对比,结果见表2所列。计算结果表明,针对不同气隙长度的电机,解析法和有限元法计算得到电磁推力的相对误差基本在5%以内,满足工程分析的需要。

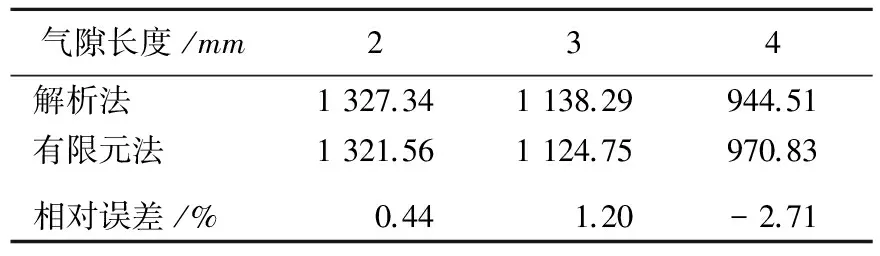
表2 不同气隙长度的电机推力 N

在与FH-PMLSM的永磁体用量相等的条件下,本文采用解析法计算了具有不同气隙长度的FW-PMLSM的电磁推力值[12],并与FH-PMLSM的电磁推力解析值进行了比较，结果见表3所列。从计算结果可以看出,本文提出的FH-PMLSM与传统的FW-PMLSM相比,电磁推力明显增加,增幅比在15%左右,且随着气隙长度的增加,推力增幅比逐渐下降。

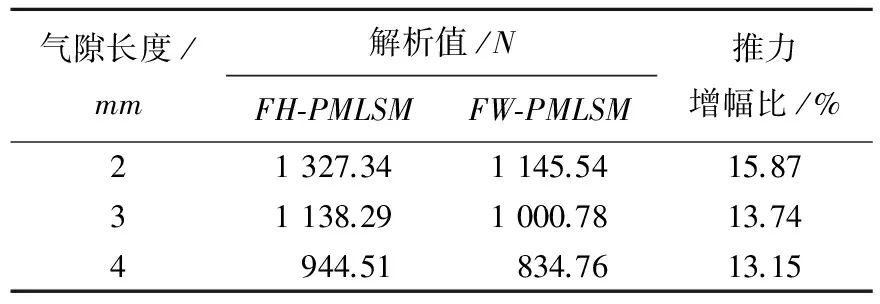
表3 2种电机的电磁推力解析值

6 结 论

本文将Halbach永磁体等效成2个无限薄的电流层和位于两者之间的体电流,在分层解析模型的基础上,利用矢量磁位和边界条件对分数槽Halbach永磁直线电机的励磁磁场进行了求解分析,并运用分布式卡式系数改进磁场计算精度,而且在该解析方法的基础上计算了不同气隙长度下的电机推力。有限元结果表明:解析计算与有限元仿真的结果基本吻合,满足工程计算精度的要求,程序运行时间只需十几秒,大幅度地缩短了求解时间,降低了计算规模,为FH-PMLSM的进一步优化设计提供了依据。此外,从2种电机的推力解析值可以看出,本文提出的FH-PMLSM的电磁推力更大,在垂直提升系统中的应用价值更高。

本文对Halbach永磁阵列的电流密度等效,恰好完整体现了永磁体激励源的作用位置和大小,从永磁体和电枢绕组等效电流密度的公式看出,理论上任意极槽配合的电机都可采用本文所提的解析方法进行磁场计算分析,这给此类电机的快速优化设计带来了极大的便利。

[1] ZHU Z Q,HOWE D.Electrical machines and drives for electric hybrid,and fuel cell vehicles[J].IEEE Proceedings, 2007, 95(4):746-765.

[2] 王玉彬,孙建鑫.分数槽集中绕组嵌入式永磁同步电机设计[J].电工技术学报,2014,29(5):70-76.

[3] 崔皆凡,蒋莉莉,王贺敏,等.Halbach磁体结构应用于永磁直线同步电机的研究[J].沈阳工业大学学报,2007,29(4):400-403.

[4] 黄学良,张前,周赣.一种无铁Halbach型永磁直线电机[J].电工技术学报,2010,25(6):1-6.

[5] 张鲁,寇宝泉,赵斌超,等.新型Halbach次级结构永磁同步直线电机[J].电工技术学报,2013,28(7):39-45.

[6] ZHOU G,HUANG X L,JIANG H,et al.Analysis method to a Halbach PM ironless linear motor with trapezoid windings [J].IEEE Transactions on Magnetics,2011,47(10):4167-4170.

[7] EL-REFAIE A M.Fractional-slot concentrated windings synchronous permanent magnet machines: opportunities and challenges[J].IEEE Transactions on Industrial Electronics,2010,57(1):107-121.

[8] 何庆领,王群京.低速永磁风力发电机的参数分析及优化设计[J].合肥工业大学学报(自然科学版),2011,34(9):1317-1320.

[9] 林福,左曙光,马琮淦,等.考虑开槽的分数槽集中绕组永磁同步电机电枢反应磁场解析计算[J].电工技术学报,2014,29(5):29-35.

[10] 上官璇峰.分段初级永磁直线同步电机理论与实验研究[D].西安:西安交通大学,2006.

[11] 许孝卓,汪旭东,封海潮,等.分数槽集中绕组永磁同步直线电机磁场解析计算[J].电工技术学报,2015,30(14):122-129.

Magneticfieldcalculationoffractional-slotHalbachpermanentmagnetlinearsynchronousmotor

SHI Yufei, WANG Xudong, XU Xiaozhuo, FENG Haichao

(School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000, China)

Fractional-slot Halbach permanent magnet linear synchronous motor(FH-PMLSM), which has secondary permanent magnet with Halbach array and primary winding with concentrated winding of non-overlapping ends, possesses the merits of high thrust density and low power losses and is especially suitable for the long stroke transportation and large thrust system. The multilayer analytical model of a FH-PMLSM prototype with 16 poles and 15 slots is presented based on the current density equivalence of Halbach array. Combined with the distributed Carter coefficient function, the magnetic fields of FH-PMLSM generated by permanent magnet are analyzed and calculated according to the analytical flux formulas of air gap field, slot field and permanent magnet field derived by vector potential and boundary conditions. And the electromagnetic force of FH-PMLSM with different air gap length is calculated by using the analytical method. It is shown that the results of the analytical calculation are consistent with those of the finite element calculation, thus verifying the correctness of the analytical method. The study can provide references for the engineering analysis and optimization of the FH-PMLSM.

Halbach permanent magnet linear synchronous motor; multilayer analytical model; fractional-slot concentrated winding; distributed Carter coefficient; magnetic field calculation

2016-04-15；

2016-06-16

国家自然科学基金资助项目(61074095);河南省教育厅自然科学研究资助项目(13A470337)和河南省国际合作资助项目(144300510014)

师宇飞(1991-),男,山西长子人,河南理工大学硕士生;

汪旭东(1967-),男,江西景德镇人,博士, 河南理工大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.12.008

TM359.4

A

1003-5060(2017)12-1619-05

(责任编辑张 镅)