基于非线性降维的合成生物元件可视化

李荣灿, 杨矫云, 王海鹏

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

基于非线性降维的合成生物元件可视化

李荣灿, 杨矫云, 王海鹏

(合肥工业大学 计算机与信息学院,安徽 合肥 230009)

合成生物学中标准化元件数量多、种类杂,使得构建生物设备时难以选择标准化元件,将这些元件可视化有助于提高生物设备构建效率。考虑生物元件为长度不一的基因短序列,文章通过结合编辑距离与高斯核函数构建生物元件距离矩阵,使用拉普拉斯特征映射方法将生物元件序列降为二维或三维数据；通过图形化展示,功能类似的生物元件可有效地聚类,功能差异大的元件可有效地区分,且对降维后数据聚类显示的二分类精度达到91.6%,三分类精度达到82.4%。实验结果表明，降维后的数据具有良好的区分度,通过降维可视化将显著提高标准化元件的选择效率。

可视化;合成生物学;非线性降维;编辑距离;聚类

当前合成生物学的可视化多集中于设备构造过程的可视化,如Pigeoncad[1]、TinkerCell[2]、VisBOL[3]等软件。这些软件通过构建生物元件的可视化符号,将生物设备的构建过程进行形象化展示,从而促进生物设备的设计。当前合成生物学的迅猛发展,标准生物元件库已积累三万多个标准生物元件,在构建生物设备时,如何进行元件选择是一件耗时费力的工作。考虑到合成生物标准元件种类多、数量大,若将生物元件进行可视化展示,具有不同功能的元件可有效区分,则可降低合成生物元件选择时的复杂程度,提高生物设备的合成效率。

生物元件为基因片段,当前也有若干基因可视化方法,如Cytoscape[4]、ParaView[5]等,这些方法多是对单个基因组可视化,从而形象化展示基因内部结构。而本文期望能够对生物元件进行可视化聚类,这对当前的方法提出了挑战。

对生物元件可视化聚类的一个思路是数据降维。当前数据降维主要分为线性降维与非线性降维。线性降维以主成分分析(principal component analysis,PCA)为主要代表[6],通过将原始数据进行线性变换,消除属性相关项;非线性变换以局部线性嵌入(locally linear embedding,LLE)[7]、拉普拉斯特征映射(Laplacian eigenmaps,LE)[8]为主要代表,通过维持原始数据的流行结构,使得降维后的数据与原始数据维持结构一致。鉴于标准生物元件为长度不一的文本序列,难以直接对其进行线性变换,同时非线性变换中的局部关系构建也不适用于序列文本数据,因此需要构建一种针对长度不一的基因文本序列进行降维可视化的方法。

本文通过改进拉普拉斯特征映射来进行合成生物标准元件可视化。首先采用编辑距离构建生物元件的距离矩阵,并利用高斯核函数进行距离映射,然后借助映射后的距离矩阵构建拉普拉斯矩阵,最后进行特征分解完成数据降维并可视化。通过在合成生物标准元件库上的应用,实验结果表明，本文提出的可视化方法可有效区分具有功能差异的生物元件,通过聚类发现,2类元件和3类元件的聚类精度分别达到91.6%和82.4%。这不仅为合成生物学家提供了一种利用可视化快速选择元件的方法,也提供了一种有效分类生物元件序列的方法。

1 算法流程介绍

标准生物元件为长度不一致的基因片段序列,传统基于欧氏距离的方法难以有效衡量生物元件的相似性,因此本文算法主要采用编辑距离进行生物元件相似性度量。通过结合编辑距离与拉普拉斯特征映射,对生物元件序列降维,达到序列数据可视化的目的。该主要过程步骤如下:

(1) 相似度计算。使用编辑距离作为衡量数据间距离的标准,并进行归一化处理,以构建表征数据集的加权无向图矩阵。

(2) 非线性降维。构建拉普拉斯矩阵,进行矩阵分解,得到降维后的数据。

(3) 可视化。将降维后的数据以图形化方式进行展示。

1.1 距离矩阵构建

编辑距离,又称Levenshtein距离,是指2个字串之间由一个转成另一个所需的最少编辑操作次数[9]。通常,编辑距离越小,2个字符串的相似度越高。例如计算TAGAA→TGACA的编辑距离为2,TAGAA到TGACA编辑操作转换过程如图2所示。

图1 TAGAA到TGACA编辑操作转换过程

当前编辑距离的计算主要是基于动态规划算法[10]。给定2条长为m、n的序列x、y,动态规划算法构建大小为m×n的矩阵E其中的每个值Ei,j表示子序列x1x2…xi和y1y2…yj中xi与yj的最小编辑距离。Ei,j的计算公式为:

其中,δ(xi,-)、δ(-,yj)分别为插入、删除的得分。若xi=yj,则δ(xi,yj)表示匹配得分;若xi≠yj,则δ(xi,yj)表示错配得分。

DNA序列TAGAA和TGACA的动态规划矩阵见表1所列。以(3,3)格计算为例，取如下3个值的最小值填入单元格。

(1) 若最上方的字符等于最左方的字符,则取左上方的数字;否则取左上方的数字加1(对于(3,3)格来说为3)。

(2) 左方数字加1(对于(3,3)格来说为2)。

(3) 上方数字加1(对于(3,3)格来说为2)。

矩阵右下角的值即为2条序列的编辑距离。

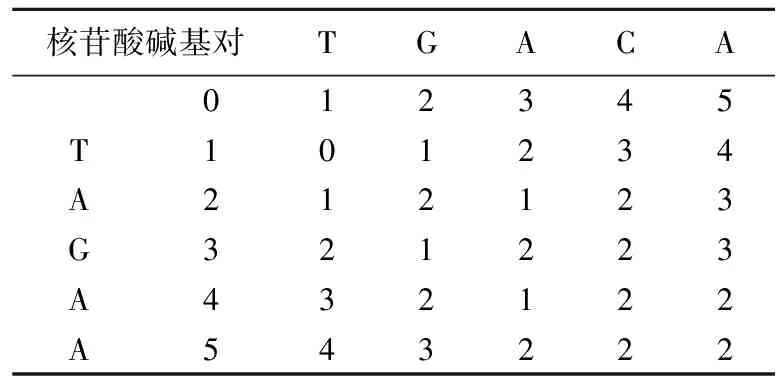
表1 TGACA和TAGAA的动态规划矩阵

编辑距离与2条序列的长度相关,其长度为:

因为降维可视化是要得到不同序列间的相似程度,所以计算出编辑距离值后应对其进行归一化处理,即用ED(x,y)值除以2个序列中较长序列的长度(maxLength(|x|,|y|)值)。编辑距离与2条序列的长度相关,长为m、n的序列间的编辑距离最大为max(m,n),即最长序列的长度。

得到归一化距离后,为使距离矩阵具有更好的局部性,本文对计算得到的编辑距离使用径向基函数核做高斯化处理,定义为:

1.2 拉普拉斯特征映射

拉普拉斯特征映射是非线性降维的主要方法,其主要思想是保证2个很相似的数据在降维的子空间里尽可能接近。假设数据实例xi、xj降维后数据实例为yi、yj,则拉普拉斯特征映射的目标函数为:

其中,Wi,j为实例xi、xj相似度。传统拉普拉斯特征映射采用欧氏距离等计算相似度,本文通过(2)式计算得到实例间的距离矩阵,从而更好地刻画不同基因序列间的相似度。

(4)式中目标函数的求解可转化为最小化目标函数yTLy,再通过矩阵分解进行计算。因此拉普拉斯特征映射的主要步骤为:

(1) 采用特定的距离衡量方法,得到所有点间的相似度值,并构建一个相似度矩阵W,本文使用编辑距离来确定,即

Wi,j=K(xi,yj)

(5)

(2) 借助W和度矩阵D(D是由di构成的对角矩阵)计算拉普拉斯矩阵L,并计算其特征值与特征向量,即

L=D-W

(7)

Ly=λDy

(8)

(3) 取最小的k个非零特征值对应的特征向量作为LE算法的结果输出,得到降维后的数据结果。

1.3 算法流程

本文算法的详细流程为:

(1) 计算任意2条序列x、y间的编辑距离ED(x,y),并依据(2)式进行标准化处理。

(2) 利用步骤(1)的距离计算结果构造距离相似度矩阵W。

(3) 对步骤(2)的矩阵W进行高斯化处理,其中参数σ需要不断调整以实现好的聚类效果。

(4) 计算度矩阵D。具体公式如下：

(5) 将度矩阵D和邻接矩阵W相减得到拉普拉斯矩阵L。

L=D-W

(12)

(6) 再通过对相似矩阵进行特征分解得到特征向量。

Ly=λDy

(13)

(7) 取最小的k个非零特征值对应的特征向量作为LE算法的结果输出,得到降维后的数据结果,并进行可视化展示。

2 实验结果

本文从合成生物学标准元件数据库中选取了3类生物元件,即复合部件(composite)、核糖体绑定位点(ribosome binding site,RBS)、引物(primer)来检验算法分类效果。其中复合部件数目为200,核糖体绑定位点数目为300,引物数目为300。实验中的参数σ取值为0.3。

2类组件的可视化结果如图2所示。图2a表示复合部件与引物的可视化结果,其中深色代表复合部件,浅色代表引物;图2b表示复合部件与核糖体绑定位点的可视化结果,其中深色代表核糖体绑定位点,浅色代表复合部件。图2中不同颜色和符号代表不同类型的元件,可以看出,同一类型的元件会聚集在一起,不同类型间的元件会有较大差距。这说明本文的可视化方法可以很好地区分不同的元件,使得用户可依据功能差异进行元件选择。

3类元件的三维可视化结果如图3所示。由图3可以看出,浅色代表的复合部件与其他2类元件具有显著差异性,而深色(左侧下方)代表的核糖体绑定位点与深色(左侧上方)代表的引物之间差别相对较小,但也可明显看出两者之间具有明显聚类。产生这种现象的原因是复合部件是由不同元件构成的复合体,功能复杂,而核糖体绑定位点与引物相对简单,差异性较小。这也反映了本文基于编辑距离的可视化很好地区分出了不同元件的功能。

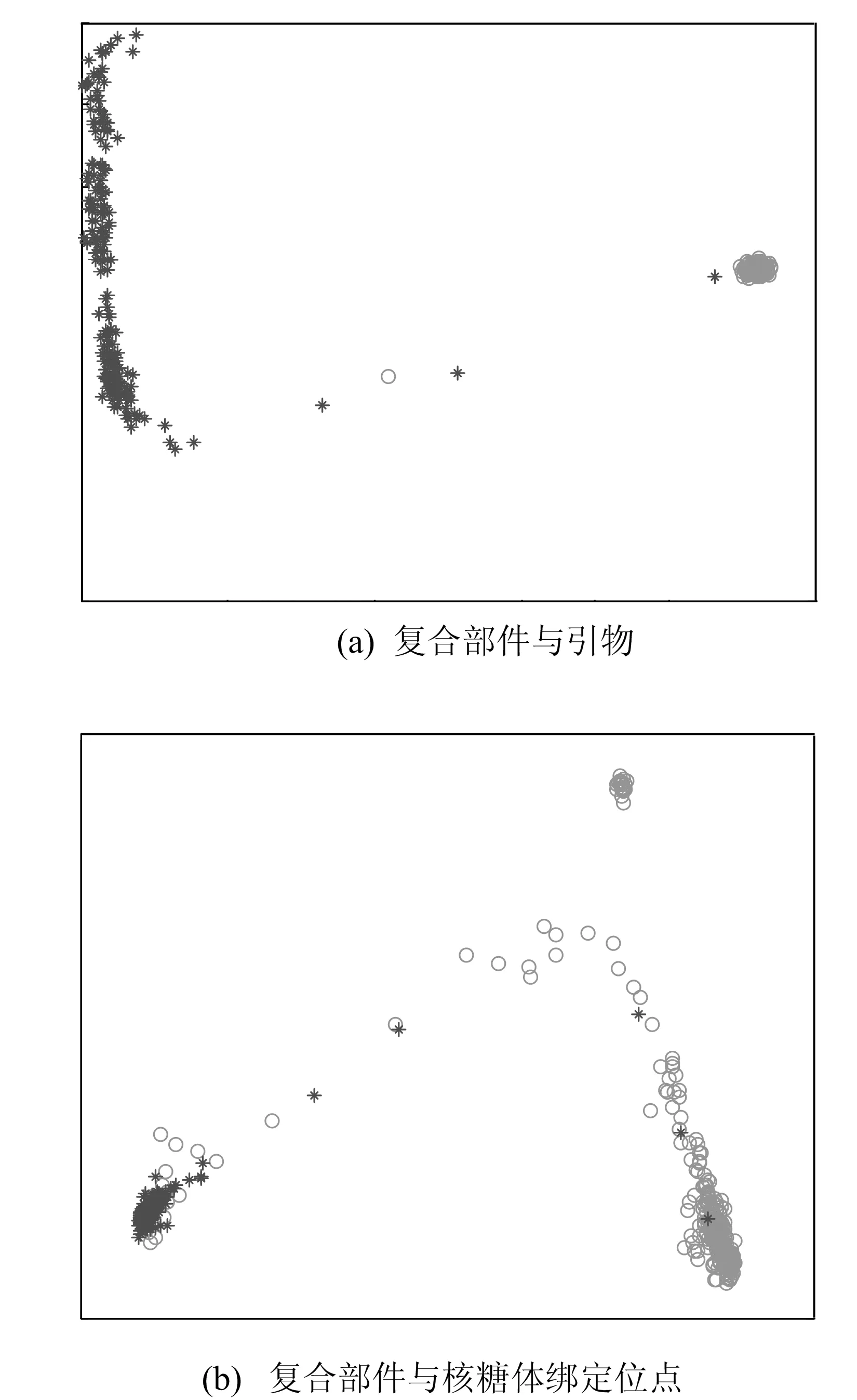
图2 2类组件的可视化结果

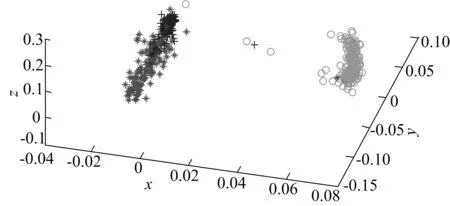
图3 复合部件、核糖体绑定位点和引物的可视化结果

使用k-means算法对3类降维可视化的数据进行聚类,结果如下:对于2种合成元件的组合,复合部件与引物、复合部件与核糖体绑定位点的分类准确率分别为99.2%、91.6%;对于3种合成元件的组合,复合部件、引物与核糖体绑定位点的分类准确率为82.4%。可见降维后的数据具有较好的区分度。这里的准确率是指聚类后与元件的原类型相比正确分类的比率。

3 结 论

本文针对多类型的大规模合成生物元件数据集进行降维可视化,通过将编辑距离与高斯核函数相结合,建立不同元件间的相似度关系矩阵,然后基于此相似度关系进行拉普拉斯特征映射,达到元件降维目的。通过观察降维后的数据可视化结果,表明不同类型的元件可构成不同聚类,功能差异性在图中表现出了距离差异性，从而说明合成生物学者依据可视化的结果帮助进行元件选择的可能性。

[1] BHATIA S,DENSMORE D.Pigeon:a design visualizer for synthetic biology[J].ACS Synthetic Biology,2013,2(6):348-350.

[2] CHANDRAN D,BERGMANN F T,SAURO H M.TinkerCell:modular CAD tool for synthetic biology[J].Journal of Biological Engineering,2009,3(1):1-17.

[3] MCLAUGHLIN J A,POCOCK M,MISIR G,et al.VisBOL:web-based tools for synthetic biology design visualization[J].ACS Synthetic Biology,2016,5(8):874.

[4] SHANNON P,MARKIEL A,OZIER O,et al.Cytoscape:a software environment for integrated models of biomolecular interaction networks[J].Genome Research,2003,13(11):2498-2504.

[5] HENDERSON A,AHRENS J,LAW C,et al.The paraview guide[M].New York:Kitware,2004.

[6] KARL PEARSON F R S.LIII.On lines and planes of closest fit to systems of points in space[J].Philosophical Magazine Series 6,2010,2(11):559-572.

[7] ROWEIS S T,SAUL L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.

[8] BELKIN M,NIYOGI P.Laplacian eigenmaps and spectral techniques for embedding and clustering[J].Advances in Neural Information Processing Systems,2001(14):585-591.

[9] LI Y J,LIU B.A normalized levenshtein distance metric [J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2007,29(6):1091-1095.

[10] JONES N C,PEVZNER P A.An introduction to bioinformatics algorithms [M]//An introduction to bioinformatics algorithms.Massachusetts:MIT Press,2004:626-626.

Visualizationofstandardsyntheticbiologicalpartsbasedonnonlineardimensionalityreduction

LI Rongcan, YANG Jiaoyun, WANG Haipeng

(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

In synthetic biology, there are a number of standard parts with a wide variety of categories, making it hard to choose a part when constructing devices. Visualizing these parts could simplify the part selection. Considering that synthetic biological parts are DNA segments with various lengths, the similarity of these parts is evaluated by the integration of edit distance and Gaussian kernel. Based on the similarity, Laplacian Eigenmaps is employed to reduce data dimensions to two or three dimensions. By visualizing the reduced data, the parts with similar functionality could cluster together, and the parts with different functionality could be separated efficiently. Besides, the cluster accuracy for two kinds and three kinds of parts reaches 91.6% and 82.4%, respectively, which proves the discrimination of the reduced data, and this could significantly improve the efficiency of parts selection.

visualization; synthetic biology; nonlinear dimensionality reduction; edit distance; clustering

2016-04-05；

2016-05-16

国家自然科学基金资助项目(61502135);中央高校基本科研业务费专项资金资助项目(JZ2015HGBZ0111)和国家高等学校学科创新引智计划资助项目(B14025)

李荣灿(1990-),男,福建泉州人,合肥工业大学硕士生;

杨矫云(1987-),男,山东招远人,博士,合肥工业大学副教授,通讯作者，E-mail:jiaoyun@hfut.edu.edu.cn.

10.3969/j.issn.1003-5060.2017.12.006

TP317.4

A

1003-5060(2017)12-1610-04

(责任编辑胡亚敏)