基于Kelly公式的仓位管理策略及经验证据
2018-01-09王志强东北财经大学金融学院辽宁大连116025
王志强,张 聪(东北财经大学 金融学院,辽宁 大连 116025)
·金融与投资·
基于Kelly公式的仓位管理策略及经验证据
王志强,张 聪
(东北财经大学 金融学院,辽宁 大连 116025)
基于Kelly公式及其扩展模型,本文在仓位管理理论分析的基础上,用中国A股市场部分指数对最优仓位估计和仓位管理策略进行了经验分析。研究结果表明:(1)中国A股市场中存在实现资产长期增长率最大化的最优仓位,进行仓位管理是有利可图的。(2)仓位管理的额外回报源于其高杠杆。(3)简单动态仓位管理策略无法达到最优仓位,会造成资产的重大损失。(4)经波动率调整的动态仓位管理策略能够显著提高资产增长率,但不能完全战胜买入持有策略。(5)买卖信号增强的经波动率调整的动态仓位管理策略能够完胜买入持有策略,尤其是对偏重于大市值的指数效果更佳。
Kelly公式;仓位管理;波动率;交易杠杆;技术分析
一、问题的提出
仓位(Position)指投资者的风险资产市值占其总资产(风险资产+无风险资产)市值的比率。仓位与组合之间的区别在于,仓位考察某类或某种风险资产占总资产的比率,而组合考察不同种类资产之间的比重。仓位管理关注的是风险资产价格波动给投资者带来的损失,仓位管理的目标是使得投资者资产的长期增长率最大,是一个多期投资决策问题,其核心在于应对风险资产收益波动的不对称性;组合选择关注的是不同种类资产之间的搭配给整个组合带来的收益与风险变化,组合选择的目标是组合的效用最大化,是一个单期投资决策问题,其核心在于应对不同资产收益之间的相关性。
仓位管理的一个理论基础是Kelly公式,它是Kelly[1]通过研究博彩者在追求财富长期增长最大化的目标下如何选择投注而得到的。Kelly[1]的研究结果显示,在一个可以进行无限次投注的博彩游戏中,博彩者每次按其财富的某一比率(被称之为最优投注比率)进行投注,可以使得自己的财富长期增长最大。当然,该模型假设博彩者的财富是无限可分的,且所有财富(包括本金和利润)都可以用于博彩游戏。将Kelly公式应用到股票市场,计算出其最优投注比率,就是我们需要的最优仓位[2]。考虑到股票价格的波动特点,其中需要假设:(1)投资者的目标是使资产长期增长率最大化。(2)每期投资仅在股票资产(可以是个股也可以是股票组合或指数)和现金之间选择。(3)股票价格变动遵循几何布朗运动,这意味着股票短期收益率近似服从正态分布,每期收益率独立同分布。结果显示,最优仓位与股票收益率的期望值正相关,与股票收益率的方差负相关。投资者应根据对未来收益率及其波动的预期来决定做多还是做空,是加仓还是减仓,是提高杠杆还是降低杠杆。简言之,由于股票收益波动存在不对称性,最优仓位能够让投资者在损失的情况下不至于伤筋动骨,在盈利的情况下尽可能实现快速增值。
后续的相关研究主要围绕上述三个假设或放松或扩展进行展开:(1)由于资产长期增长率的目标函数中没有考虑风险因素,因而许多研究者将该目标函数扩展到包含风险的各种效用函数。(2)部分研究将一项风险资产扩展到多项风险资产,并考虑各项风险资产之间的相关性。(3)考虑风险资产的收益率并不独立同分布于正态分布,而是具有尖峰厚尾和时间序列相关特性,因而部分研究主要采用经验研究方法考察Kelly公式的实用效果。
在目标函数方面,Samuelson[3]将最大化资产长期增长的目标函数换成幂效用函数考察最优仓位,研究结果显示,最优仓位独立于投资者的财富水平,每期中投资者根据其总资产的某一比率投资于风险资产。Hakansson[4]采用四种效用函数(包括正幂效用函数、负幂效用函数、对数效用函数和指数效用函数)将Samuelson[3]的研究问题扩展到更一般的形式,得到类似结果。Merton和Samuelson[5]将最大化资产长期增长的目标函数简单直接地扩展为对数效用函数,结果发现将其用于多期投资决策时风险较高。Miller[6]的研究结果表明,当投资期限趋近无穷大时,最大化资产的期望对数效用函数所得到的投资比重是最优的,此时资产的长期增长率主要取决于资产的期望收益率。Aucamp[7]的研究结果显示,在跨期和不确定环境中,采用最优仓位策略进行投资的话,需要非常长的投资期限才能实现资产长期增长最大化的目标。但从中期来看,只要资产风险较小,最优仓位策略优于其他策略。Maclean等[8]模拟了Kelly最优仓位策略中期运行效果,其研究表明Kelly最优仓位策略不但可以实现资产长期增长的最大化,而且能够避免破产的发生,另外还优于所有其他策略。
扩展到多项资产情形,Maslov和Zhang[9]假设组合中各资产价格变动遵循多维几何布朗运动,将单项资产形式扩展到多项资产形式,得到与单项资产形式类似的结果。Medo等[10]考察了相互独立的多项资产情形,结果显示,在不超过5项资产的情形下,能够得出最优仓位的解析解;超过5项资产,只能采用数值方法近似求解。Medo和Zhang[11]考察了存在相关性的多项资产情形,结果发现,组合中风险资产之间的正相关会导致组合中资产的配置比重相应减少。
在经验分析方面,Samuelson[12]的研究结果显示,从长期来看,采用最优仓位策略的基金经理将获得更多的资产增长;即使风险资产的期望收益为正,Kelly最优仓位策略在长期投资期限内也可能出现亏损,在实际运用时要做好风险控制;相对于基于其他效用函数的仓位管理策略,Kelly最优仓位策略最优。Rotando和Thorp[13]基于S&P500指数考察了Kelly最优仓位策略的实用效果,发现其具有相对比较优势。Maclean等[14]基于资产增长与安全的测度方法考察了动态投资过程中资产增长与安全问题,研究表明,风险资产的配置比重不能超过Kelly最优仓位。如果风险资产的配置比重超过Kelly最优仓位,投资风险增加,资产增长率降低,他们认为Kelly最优仓位策略优于其他策略。Anderson和Faff[15]用五分钟高频期货数据对Kelly最优仓位策略进行回测和检验,结果表明,仓位管理策略在期货交易中非常重要,只有清楚仓位管理的可行范围,才能避免破产,同时实现资产长期增长率的最大化。
国内对基于Kelly公式的仓位管理研究相对较少。凌士勤[16]提出了基于VAR及Kelly增长体系的“基于最优增长路径的增长-安全模型”,并在离散条件下,用基于情景分析的方法考察了模型的实用效果,他认为该模型可作为投资活动的一种实践工具。罗勇[17]基于Kelly理论,建立了风险约束下的Kelly动态投资组合模型,采用理论模型和经验分析研究了在最大资金衰落与交易成本约束下的基金资产动态最优增长问题。
综上所述,笔者认为,已有的相关研究存在两个不足:第一,理论模型的假设与现实不完全相同致使Kelly最优仓位管理策略的效果无法保证。事实上,许多证据显示风险资产收益率并不独立同分布于正态分布,而是具有尖峰厚尾和时间序列相关特性,这要求Kelly最优仓位管理策略的实效性需要回测与检验。第二,已有的国内外相关研究并没有告诉我们Kelly最优仓位管理策略在中国A股市场中是否适用。鉴于此,本文尝试采用中国A股部分指数对Kelly最优仓位管理策略进行回测和检验,在此基础上寻求更好的仓位管理策略。
本文的可能贡献在于:第一,首次尝试采用中国A股市场指数回测与检验最优仓位的存在性,我们确定最优仓位存在于中国A股市场,且其额外回报来源于投资者对交易杠杆的使用。第二,首次提出采用波动率调整和买卖信号增强的方法动态调整仓位,经验检验结果证明该方法可以极大地提高投资者的收益率。
二、基于Kelly公式的仓位管理理论分析
(一)基本模型:Kelly公式
假设一个博彩者的初始财富为W0,该博彩者可以将其财富的一部分不断重复地投入到一个风险游戏中。每轮游戏中,博彩者赢的概率为p,输的概率为1-p,如果获胜,博彩者可以得到投注的两倍,否则失去投注。若每轮游戏中博彩者的收益率为Rt,则博彩者赢时Rt=1,博彩者输时Rt=-1。若博彩者每次下注比率(或投入比率,我们称之为仓位)为f,那么T期期末投资者的财富WT为:
(1)
由于每轮游戏中博彩者的收益率Rt可以视为独立同分布于两点分布(1,-1; p,1-p),因而博彩者的资产长期指数增长率为[1]:
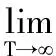
(2)
最大化式(2)获得最优仓位为:
f*=(2p-1)×100%
(3)
式(3)显示,如果赢的概率大于1/2,博彩者就下注,其最优下注比率随着概率增加而增加。譬如,赢的概率p=0.6000时最优下注比率为20%,此时博彩者的资产长期指数增长率为2.03%。
(二)扩展模型:Kelly公式的扩展
将Kelly公式应用到股票市场,同时考虑到股票市场的特点,我们假设投资者每期的收益率独立同分布于两点分布(rw, -rl; p, 1-p),则投资者的资产长期指数增长率为:
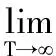
(4)
最大化式(4)可以得到最优仓位为:
f*=[prw-(1-p)rl]/rwrl×100%=E(R)/rwrl×100%
(5)
式(5)显示,如果期望收益为正,投资者应该做多;如果期望收益为负,投资者应该做空。投资者的最优仓位大小与期望收益正相关,与rwrl负相关。实际上,由于该两点分布的方差为Var(R)=p(1-p)(rw+rl)2,可以证明,当p和E(R)固定不变的情况下,rwrl会随着方差Var(R)增加而增大。因此,我们可以推出,该两点分布的方差越大,最优仓位f*越小。这意味着,投资者的最优仓位大小与两点分布的方差负相关。
考虑到股票收益率服从两点分布的假设较为特殊,我们将假设改为常用的假设:股票价格S的变动遵循几何布朗运动,即dS=Sdt+Sdz,在此假设下股票价格服从对数正态分布,股票的短期收益率近似服从正态分布N(-2/2,)。考虑一个由股票和无风险资产组成的组合,其仓位(或投资比率)分别为f和1-f,无风险收益率记为r,则投资者的资产长期指数增长率为:
g=fμ-1/2(fσ)2+(1-f)r
(6)
最大化式(6)可以得到最优仓位为:
f*=(μ-r)/σ2×100%
(7)
基于式(7),我们从理论上进一步证明了最优仓位与股票收益率的期望值正相关,与股票收益率的方差负相关。这表明,在收益率的方差不变的条件下,预期收益越高,最优仓位越大,投资者的资产长期增长速度就越快;在期望收益率不变的条件下,收益率的方差越大,最优仓位越小,投资者的资产长期增长速度就越快。投资者应根据对未来收益率及其波动的预期,来决定做多还是做空,是加仓还是减仓,是提高杠杆还是降低杠杆。
需要说明的是,最优仓位的计算公式建立在不同时期的投资收益是独立同分布的,且每期的仓位是固定的。实践中,很多经验证据显示股票收益具有均值回复特点,且股价波动具有聚集效应,即股价波动在一段时期内较小而下一段时期较大,周而复始。
三、最优仓位估计:来自中国A股部分指数的经验证据
(一)最优仓位测算
在下文的具体分析过程中,我们选择中国A股市场中7个主要指数对最优仓位进行回测和检验,这7个指数分别是沪深300指数、上证指数、上证50指数、上证180指数、深圳成份指数、中小板指数和创业板指数。之所以选择指数进行回测和检验,是因为指数收益率相对于个股收益率更接近正态分布,这一结果获得许多经验证据支持,同时也是因为部分指数可以通过相关的衍生产品进行杠杆交易或做空交易。我们使用这7个指数周收益率的全部样本分别估计其样本均值和样本方差,根据式(7)计算其最优仓位,这里我们不考虑闲置资金的无风险投资收益,即假设r=0,则f*=μ/σ2×100%。考虑到现行的涨跌停限制始于1996年年底,此前的股市波动幅度显著高于此后的股市,譬如,1995年5月15日至1995年5月19日上证指数上涨超过46%,1996年12月2日至1996年12月6日上证指数上涨超过17%,1996年12月16日至1996年12月20日上证指数下跌超过20%,我们对较早开始的上证指数和深圳成份指数增加了1997年之后的样本区间进行回测和检验。具体测算结果如表1所示。
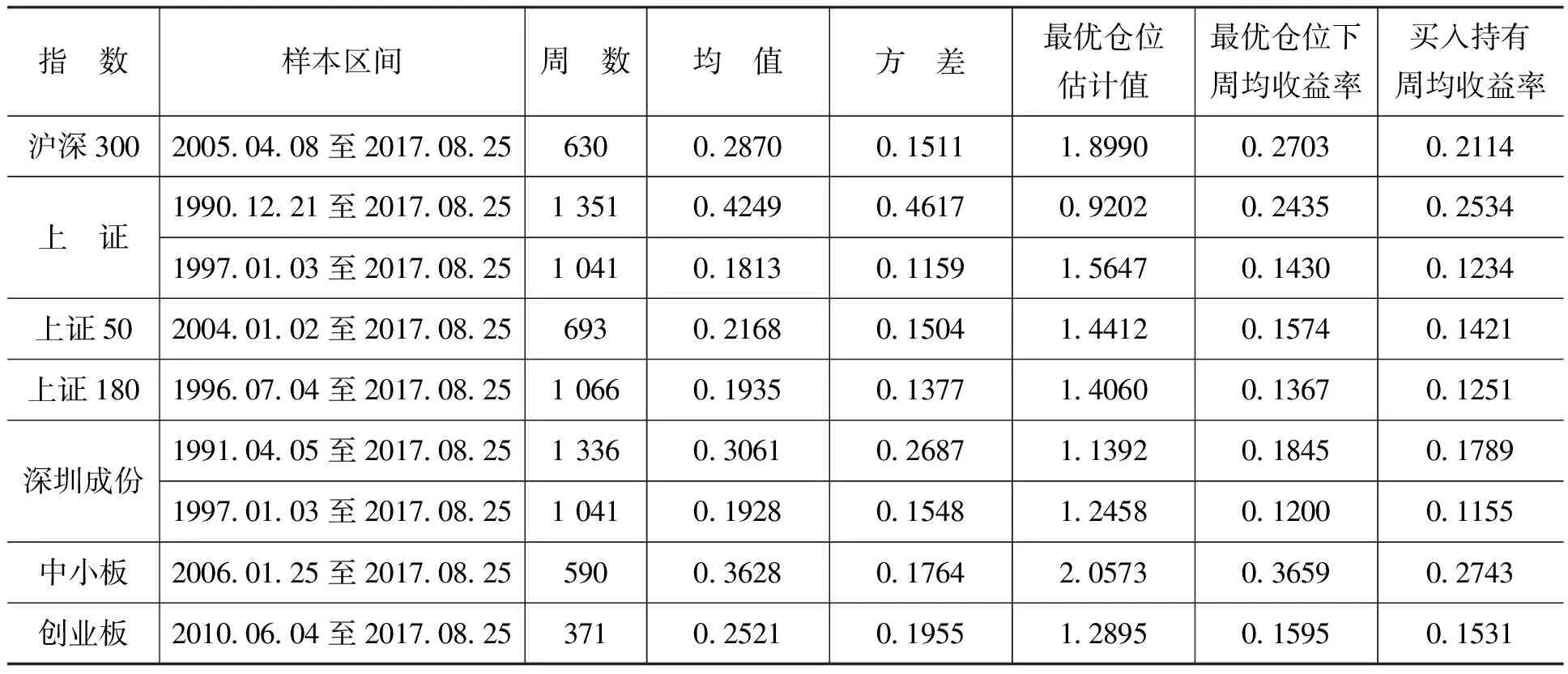
表1 基于指数的最优仓位估计与收益率测算 单位:周,%
注:周均收益率是指样本区间内总收益率的几何平均收益率。下同。
从表1可以看出,第一,除了上证指数在1990年12月21日至2017年8月25日样本区间内的最优仓位估计值下周均收益率(0.2435%)低于该区间内买入持有的周均收益率(0.2534%)之外,其他指数的最优仓位估计值下周均收益率均高于该区间内买入持有的周均收益率。这表明,有一个更好的仓位能够让投资指数的长期收益超过简单被动的买入持有收益。第二,除了上证指数在1990年12月21日至2017年8月25日样本区间内的最优仓位估计值(0.9202)小于1之外,其他指数的最优仓位估计值都大于1,这表明为实现高于买入持有策略的资产增长率,投资者应该借助杠杆手段加大仓位。第三,沪深300指数和中小板指数的最优仓位估计值下周均收益率显著高于该区间内买入持有的周均收益率,其他指数不明显。这表明,采用式(7)计算出的最优仓位估计值在实际应用时应该慎重。需要说明的是,上述经验结果并没有考虑交易成本因素的影响,部分结果在实践中的效果有待进一步考察。
(二)不同仓位下收益率测算与比较
表1的结果只能告诉我们,根据式(7)计算出的最优仓位估计值能够让投资指数的长期收益超过简单被动的买入持有收益,但是并不能说明该估计值就是最优仓位,因为我们并没有证明该最优仓位估计值下周均收益率高于其他仓位下的周均收益率。下面,我们以沪深300指数为例,考察最优仓位估计值下周均收益率是否高于其他仓位下的周均收益率,如果该估计值下周均收益率均高于其他仓位下的周均收益率,则证明该估计值是最优仓位,否则不是。为此,我们围绕沪深300指数的最优仓位估计值(1.8990),以0.1000为间隔向前向后各选择9个仓位计算其样本区间内总收益率和周均收益率,如表2所示。
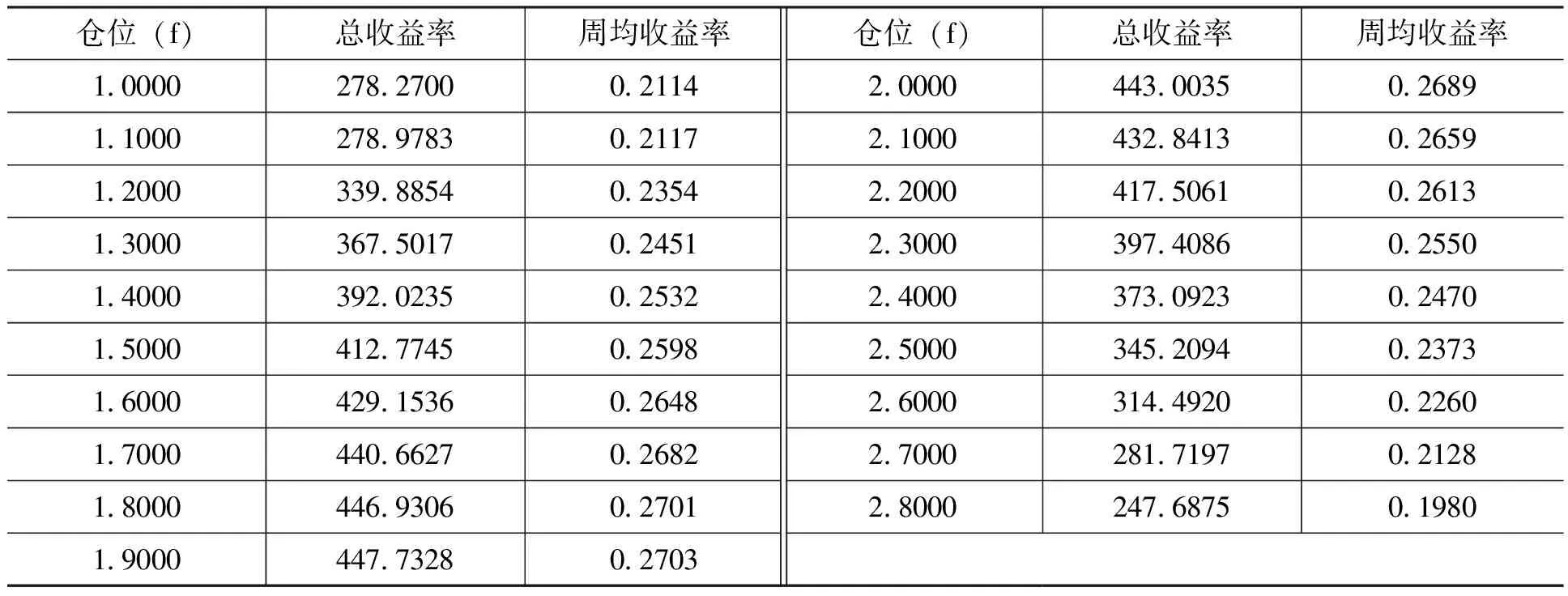
表2 不同仓位下的收益率测算:基于沪深300指数周收益 单位:%
从表2可以看出,仓位在1.9000下总收益率(447.7328%)和周均收益率(0.2703%)最高,样本区间内其他仓位下总收益率和周均收益率均相对较小。这表明,1.9000的仓位具有相对较强的长期收益优势。
为了反映全貌,我们将小于1.0000的仓位下总收益率和周均收益率也进行了计算,如图1和图2所示。很明显,在我们所考察的样本区间内最优仓位是1.9000。因此,结合从表1中得出的结果,我们认为,中国A股市场中存在资产长期增长目标下的最优仓位,仓位管理是一件应该考虑和值得去做的事情,投资者应该借助杠杆手段加大仓位,以实现资产的长期高增长。
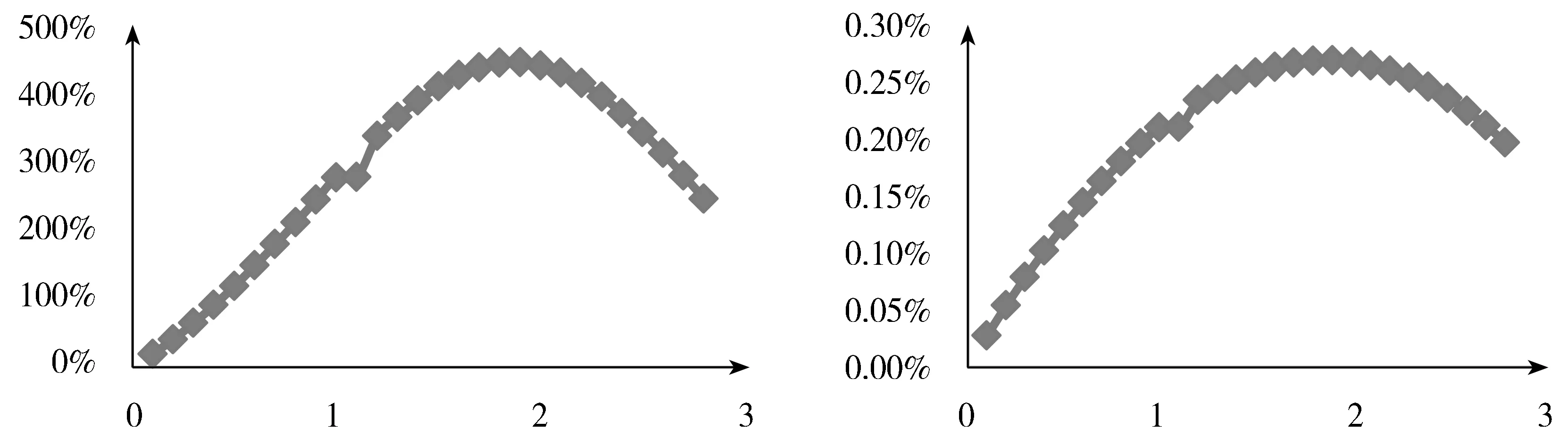
图1 总收益率随仓位大小的变化 图2 几何平均收益率随仓位大小的变化
四、动态仓位管理策略的经验证据
上文对最优仓位的估计与检验中,采用的是固定仓位方法,即整个样本区间内仓位是固定的,但是这可能会引起前视偏差(Look-Ahead Bias),在实践中是行不通的。因此,实际操作中我们必须根据可获取的相关数据,判断是否采取动态调整仓位的管理策略进行仓位管理。本部分我们检测简单动态仓位管理策略、经波动率调整的动态仓位管理策略、考虑买卖信号的简单动态仓位管理策略和考虑买卖信号的经波动率调整的动态仓位管理策略。
(一)简单动态仓位管理策略
一种最简单的动态仓位管理策略是基于当期已有数据估计收益率的期望和方差,根据式(7)计算最优仓位,依据该最优仓位建仓,下一期加入最新数据滚动计算新的最优仓位,再依据新的最优仓位进行调仓,以此类推。我们采用过去50周(约一年)的周收益率估计当期期望和当期方差,根据式(7)计算最优仓位,然后计算当期收益率,滚动计算直至样本期结束,最后计算整个样本区间内总收益率和几何平均周收益率。具体测算结果列于表3的左边。从表3可以看出,简单动态仓位管理策略的总收益率基本上等于或接近-100%,这意味着简单动态仓位管理策略在实践中是行不通的,其原因在于短期内股价的大幅波动会导致当期期望和当期方差的估计值偏离理论值,进而引起计算出的最优仓位远离真正的最优仓位。这种情况下,依据错误的最优仓位进行建仓或调仓就会很容易被短期内股价的暴涨暴跌击穿仓位或者损失殆尽难以恢复。
(二)经波动率调整的动态仓位管理策略
借鉴Barroso和Santa-Clara[18]对动量崩溃(Momentum Crashes)的管理思想,我们的波动率调整思路是,由于波动率具有较好的预测性,可以采用自回归模型预测其未来的波动率,因而我们可以用波动率的预测值修正或者调整最优仓位,具体而言,当波动率的预测值较高时调低仓位,当波动率的预测值较低时调高仓位。经波动率调整的动态仓位用如下公式进行计算:
fm=1+(Dmax-D)/(Dmax-Dmin)
(8)
其中,D、Dmax和Dmin分别表示当期方差、过去n期内最大方差和过去n期内最小方差的估计值。
式(8)的含义是,当期方差估计值相对较大的时候仓位增加相对较小,当期方差估计值相对较小的时候仓位增加相对较大。这很容易理解,当期方差估计值相对较大意味着市场波动加大,风险增加,此时应该轻仓;当期方差估计值相对较小意味着市场波动减小,风险降低,此时应该重仓。理论上讲,我们应该在最优仓位的基础上根据波动率变化及其预测的高低进行减仓或加仓的调整,但是考虑到我们要以满仓买入持有为比较基准,分析经波动率调整的仓位管理策略的幅度和效果,因而在式(8)中我们用满仓(即“1”)取代了最优仓位,同时也对减仓或加仓的调整项,即式(8)中等号右边第二项做出了调整。
本文中,我们取n为100周(约两年),根据式(8)计算经波动率调整的动态仓位,每周滚动调整仓位。具体测算结果列于表3的中间。从表3可以看出,第一,除了上证180指数的收益率为负,总收益率和周均收益率分别为-33.6517%和-0.0448%,其他6个指数的总收益率和周均收益率均大于零。这表明,经波动率调整的动态仓位管理策略远远优于简单动态仓位管理策略。第二,7个指数中沪深300指数、中小板指数和创业板指数的收益率超过买入持有收益率,另外4个指数没有战胜买入持有策略。这表明,相对于简单动态仓位管理策略,经波动率调整的动态仓位管理策略尽管有了显著改善,但是其收益率仍然难以让人满意。
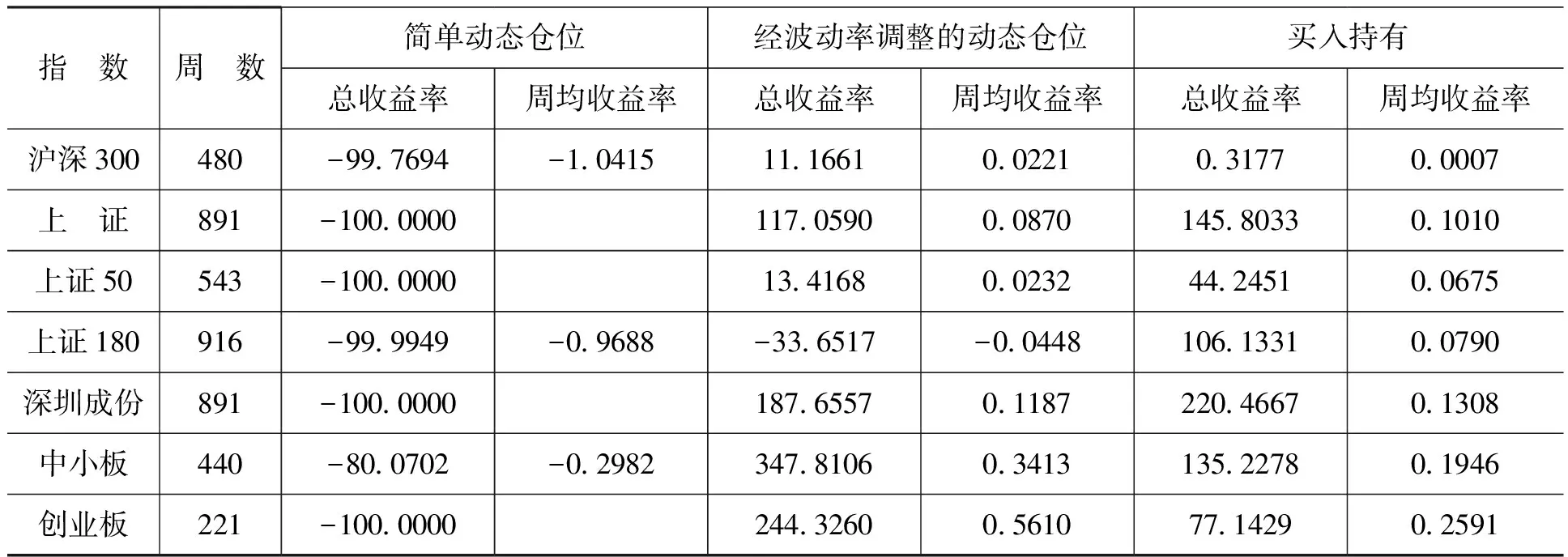
表3 动态仓位管理策略的收益率测算 单位:周,%
经过仔细分析,笔者认为,经波动率调整的动态仓位管理策略之所以没有获得令人满意的收益率,是因为我们在式(8)中根据波动率大小以负线性相关的方式进行了调整,无论什么原因,只要波动率上升就降低仓位,波动率下降就提升仓位。因此,这种调整方式没有区分波动率的变动是来源于指数的大幅上涨还是大幅下跌,从而会引起指数大幅上涨时降低仓位,进而导致收益率的下跌。为了避免这一缺陷,在下文中我们拟根据来自技术分析方法的买卖信号增强的经波动率调整的动态仓位管理策略。
(三)考虑买卖信号的经波动率调整的动态仓位管理策略
均线系统显示出金叉后股价指数通常会在均线的上方运行,均线系统显示出死叉后股价指数通常会在均线的下方运行。借助这一规律,我们引入来自技术分析方法的买卖信号增强经波动率调整的动态仓位管理策略。具体而言,均线处于多头排列发出买入信号时应该增加仓位,均线处于空头排列发出卖出信号时应该减少仓位。因此,我们将式(8)调整为:
fm=1+sign[(Dmax-D)/(Dmax-Dmin)]
(9)
其中,sign表示买卖信号,当股价指数大于其均线值时sign=1,当股价指数小于等于其均线值时sign=-1。
式(9)的含义是,当股价指数在其均线的上方时根据波动率的相对大小加仓,当股价指数在其均线的下方时根据波动率的相对大小减仓。为了便于比较,我们也考虑了买卖信号增强的简单动态仓位管理策略,即根据买卖信号直接确定简单动态仓位。具体地,当均线处于多头排列发出买入信号时仓位为正(即做多),均线处于空头排列发出卖出信号时仓位为负(即做空)。本文中,我们以5周均线为基准,当股价指数大于过去5周指数均值时根据式(9)加仓,当股价指数小于等于过去5周指数均值时根据式(9)减仓。如表4所示。
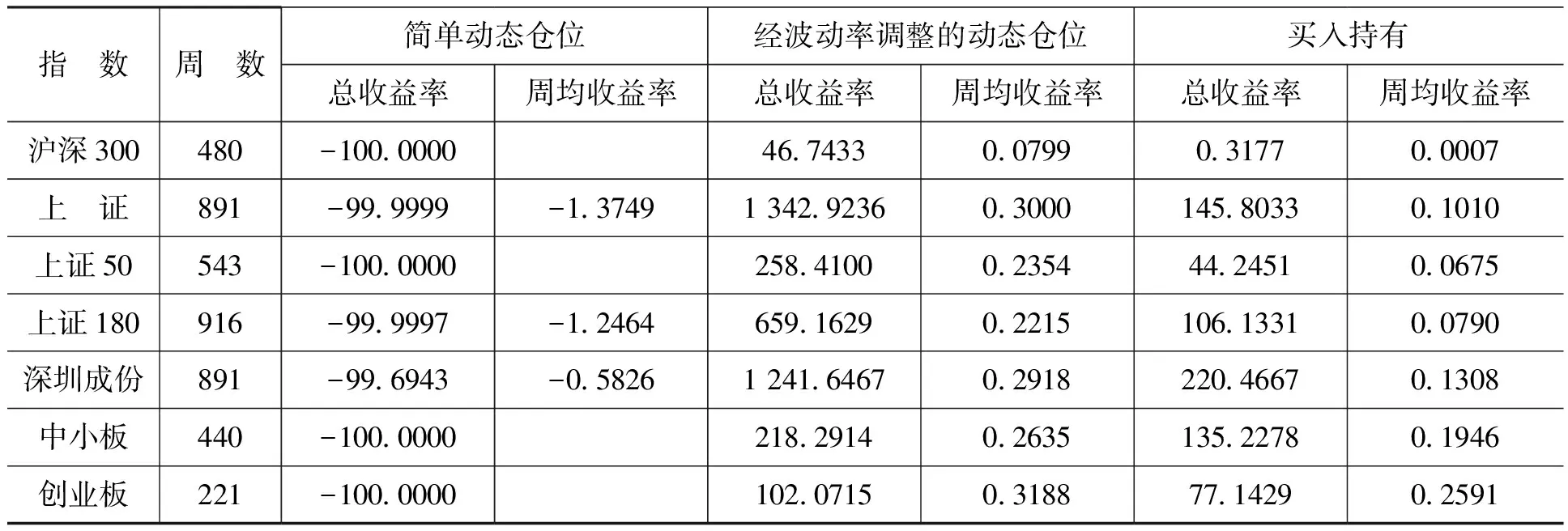
表4 买卖信号增强的动态仓位管理策略的收益率测算 单位:周,%
从表4可以看出,第一,考虑买卖信号增强的简单动态仓位管理策略与不考虑买卖信号增强的简单动态仓位管理策略一样,其总收益率全部等于或接近-100%,考虑买卖信号并没有提高仓位管理的收益率。第二,买卖信号增强且经波动率调整后,7个指数的总收益率和周均收益率均显著地高于买入持有的总收益率和周均收益率。这表明,买卖信号增强的经波动率调整的动态仓位管理策略显著地提高了仓位管理的收益率。第三,相对于经波动率调整的动态仓位管理策略,买卖信号增强的经波动率调整的动态仓位管理策略对于中小板指数和创业板指数的仓位管理效果有所下降。我们认为,其原因可能在于中小板指数和创业板指数频繁大幅波动,相对于主板指数而言它们发出的买卖信号的可靠性较差,由此造成买卖信号增强的经波动率调整的动态仓位管理策略不如不考虑买卖信号的经波动率调整的动态仓位管理策略。
五、结 论
基于Kelly公式及其扩展模型,本文在仓位管理理论分析的基础上,用中国A股市场7个主要指数(沪深300指数、上证指数、上证50指数、上证180指数、深圳成份指数、中小板指数和创业板指数)对最优仓位估计和仓位管理策略进行了经验分析。我们的研究结果表明:(1)中国A股市场中存在实现资产长期增长率最大化的最优仓位,进行仓位管理是有利可图的。因此,作为资产管理者和投资者应该重视仓位管理,选择适当的仓位管理策略寻求最优仓位,以实现资产长期增长的最大化。(2)仓位管理的额外回报源于其高杠杆。交易杠杆具有两面性,选择适当的杠杆能够提高资产的长期增长率,杠杆过高或者过低均会阻碍或损坏资产的长期增长。(3)简单动态仓位管理策略无法达到最优仓位,会造成资产的重大损失。中国A股市场仍然处于结构变化和逐渐完善之中,投资理念、投资方法和投资者情绪都在发展变化,这种情况下估计出一个与实际相近的最优仓位是较为困难的,因此,我们不能简单套用理论模型估计最优仓位,必须要根据市场波动规律调整最优仓位估计值。(4)经波动率调整的动态仓位管理策略能够显著提高资产增长率,但不能完全战胜买入持有策略。大量经验证据显示波动率具有预测性,波动率的这种预测性具有一定的应用价值,本文的经验证据也显示出波动率可以被用来改善仓位管理。(5)用买卖信号增强的经波动率调整的动态仓位管理策略能够完胜买入持有策略,尤其是对偏重于大市值的指数。
[1] Kelly, J.L.A New Interpretation of Information Rate[J].Bell System Technical Journal, 1956,35(1):917-926.
[2] Thorp, E.O.The Kelly Criterion in Blackjack Sports Betting and the Stock Market[J].Hand-Book of Asset and Liability Management, 2006, 11(1):387-428.
[3] Samuelson, P.A.Lifetime Portfolio Selection by Dynamic Stochastic Programming[J].Review of Economics and Statistics, 1969, 51(3):239-246.
[4] Hakansson, N.H.Optimal Investment and Consumption Strategies Under Risk for a Class of Utilities Functions[J].Econometrica, 1970, 38(5):587-607.
[5] Merton, R.C., Samuelson, P.A.Fallacy of the Log-Normal Approximation to Optimal Portfolio Decision-Making Over Many Periods[J].Journal of Financial Economics, 1974, 11(1):67-94.
[6] Miller, B.L.Optimal Portfolio Decision Making Where the Horizon Is Infinite[J].Management Science, 1975, 22(2):220-225.
[7] Aucamp, D.On the Extensive Number of Plays to Achieve Superior Performance With the Geometric Mean Strategy[J]. Management Science, 1993, 39(9):1163-1172.
[8] Maclean, L.C., Thorp, E.O.,Zhao, W.T.,et al.Medium Term Simulations of the Full Kelly and Fractional Kelly Investment Strategies[J].The Kelly Capital Growth Investment Criterion: Theory and Practice, 2010, 11(2):543-562.
[9] Maslov, S.,Zhang, Y.C.Optimal Investment Strategy for Risky Assets[J].International Journal of Theoretical and Applied Finance, 1998, 1(3):377-387.
[10] Medo, M., Pis’Mak, Y.M., Zhang, Y.C.Diversification and Limited Information in the Kelly Game[J].Physica A Statistical Mechanics & Its Application, 2008, 387(24): 6151-6158.
[11] Medo, M., Zhang, Y.C.How to Quantify the Influence of Correlations on Investment Diversification[J].International Review of Financial Analysis, 2009, 18(1-2):34-39.
[12] Samuelson, P.A.Why We Should not Make Mean Log of Wealth Big Though Years to Act Are Long[J].Journal of Banking and Finance, 1979, 3(4):305-307.
[13] Rotando, L.M., Thorp, E.O.The Kelly Criterion and the Stock Market[J].The American Mathematical Monthly, 1992, 99(10):922-931.
[14] Maclean, L.C., Ziemba, W.T., Blazenko, G.Growth Versus Security in Dynamic Investment Analysis[J].Management Science, 1992, 38(11):1562-1585.
[15] Anderson, J.A., Faff, R.W.Maximizing Futures Returns Using Fixed Fraction Asset Allocation[J].Applied Financial Economics, 2004, 14(15):1067-1073.
[16] 凌士勤.基于最优增长路径的多期投资组合选择及其动态调整研究[D].武汉:华中科技大学博士学位论文, 2006.
[17] 罗勇.风险约束下的Kelly动态投资组合优化[D].成都:电子科技大学博士学位论文, 2015.
[18] Barroso, P., Santa-Clara, P.Momentum Has Its Moments[J].Journal of Financial Economics, 2015,116(1): 111-120.
2017-09-10
辽宁省社会科学规划基金项目“金融冲击、企业分散度与经济风险分析”(L15CJY005)
王志强(1965-),男(蒙古族),内蒙古乌海人,教授,博士生导师,主要从事金融学、数量经济学等方面的研究。E-mail:wangzhiqiang@dufe.edu.cn张 聪(1989-),男,辽宁大连人,博士研究生,主要从事金融工程研究。E-mail:zhangcongchuck@163.com
F832.1
A
1000-176X(2017)12-0037-08
巴红静)
