基于生灭论的通信缓存区数据队长研究*
2018-01-08王亚军周圣武李金玉
王亚军,张 艳,周圣武,李金玉
(中国矿业大学)
基于生灭论的通信缓存区数据队长研究*
王亚军,张 艳,周圣武,李金玉
(中国矿业大学)
在通信网络中,基站和终端数据传输上下行的速率不同,数据成功上传之前,经常会有一定的数据包滞留在终端,这个滞留区称作缓存区.本文研究了缓存区滞留数据包的队长问题,求得了队长的绝对分布和数据包平均队长、平均滞留时间的稳态解.
生灭论;通信网络;缓存区;队长
0 引言
缓存(Cache memory)是硬盘控制器上的一块内存芯片,它是计算机硬盘内部存储和外界接口之间的缓冲器.由于硬盘的内部数据传输速度和外界介面传输速度不同,缓存在其中起到一个缓冲的作用.通信系统中,首先需要对通信网络进行建模,一个普遍的通信系统模型是一个AP接入点为一组物理设备提供服务,这里称接入点为基站,每个物理设备称为终端.基站和终端之间要进行数据的交换,它们对数据包的处理能力不同,因此基站和终端之间数据交换的上下行的速度不同.终端接收数据后上传到基站或其他终端设备前,需要对数据进行分析和处理,这段时间数据就停留在终端设备,此时终端设备就起到数据缓存区的作用.缓存区数据包的个数称为数据队长,分析缓存区数据的队长对通信系统的网络建模具有重要意义.
1 缓存区数据队长的提出
一个普遍的通信网络模型是一个基站为多个终端提供服务[1],即数据的交换.此时假设通信在n个时隙中有k个终端想要与之进行数据传输,定义Lmn为第m个终端在第n个时隙中缓存中数据包的个数(即队长),第m个终端在第n个时隙中接收数据包的概率p1(h)=λ1h+o(h),λi>0,终端向基站上行数据包的概率p2(h)=μih+o(h),μi>0,数据上传后从缓存区删除,否则继续存在于缓存区,接收的数据包在缓存区累加排队处理,按照先进先出的原则依次处理和上传数据.相邻两个数据包的上行和下行都具有一定的时间间隔,在非常短的时间间隔内只有1个数据包的上行或下行.该文考虑的是一个数据终端的队长情况,因此把Lmn简记为Lm.
2 数据队长模型
根据模型和实际情况,有如下状态转移式:

这里pi,i+1(h)表示在时间为h的间隔内,缓存区数据队长由i增加到i+1的概率,λi表示增加的速率,μi表示减少的速率,它们反映单位时间内基站和终端上下行数据包的多少.第i个终端t时刻缓存区队长Lm只依赖t-1时刻的取值,而与t-1之前的结果无关,因此队长Lm(t)是一个马尔科夫链,具体讲它是一个生灭过程,其状态空间E={0,1,2,…},状态转移仅仅在相邻的状态中进行,其状态转移图如图1所示.

图1
该生灭过程可作如下解释[2]:Lm(t)代表时刻第m个终端缓存中数据包的队长,则在很小的时隙内,缓存中队长的变化有三种可能,状态由i变到i+1,即基站向终端发送数据,缓存数据包增加一个,其概率为λih+o(h);状态由i变到i-1,缓存数据包减少一个,其概率为μih+o(h);数据包数量不变,其概率为1-λih-μih+o(h),若记状态转移矩阵p(h)=(pij(h)),I为同阶单位矩阵,则该过程的状态转移速率矩阵Q为
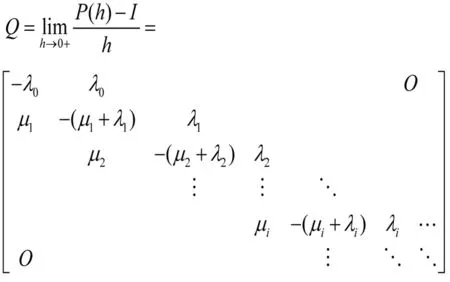
对于一般化的通信系统,假定基站向终端源源不断的发送数据,终端缓存区所允许的数据包的队长是无限的,对于终端,基站的下行数据包的到达均为Poisson到达[3],到达强度为λ.因此在长度为h的时间间隔内终端接收到一个数据包的概率为λh+o(h),多于一个数据包的概率为o(h),没有数据包到达的概率为1-λh+o(h).有泊松理论,接收到相邻两个数据包的时间间隔是独立同参数为λ的指数变量.另一方面,在长度为h的时间间隔内终端上传一个数据包的概率为μh+o(h),多于一个数据包离开的概率为o(h),没有数据包上传的概率为1-μh+o(h),上传相邻两个数据包的时间间隔是独立同参数为μ的指数变量.若记L(t),(t≥0)表示时刻缓存区的队长,其状态空间是E={0,1,2,…},于是它的Q矩阵

由柯尔莫格洛夫向后方程可得{L(t),t≥0}的绝对概率分布pj(t)=P{L(t)=j},(j∈E)满足方程
由上述Q矩阵,在t时刻缓存区数据队长所满足的微分方程为
3 数据队长的极限分布求解

k>0

该分布为几何分布.这里π0为缓存区没有数据包的概率,而1-π0表示缓存区有数据包等待的概率.
有了上述极限分布之后,不难算出下面2个缓存区在稳态时的数值参量:
(1)缓存区数据包的平均数即平均队长为
(2)数据包在缓存区的平均滞留时间,由文献[4-5]可得

4 结束语
通信系统中进行数据传输经常遇到输入和输出速率不对称的情况,基站和服务终端数据传送由于终端对数据的分析与处理也会导致上下行速率不一,终端在上行或转发数据之前会把数据暂存于缓存区,这样,数据包经常在缓存区滞留.该文研究了缓存区的数据包的队长问题,得出了其平稳分布、平均队长、平均滞留时间的稳态解.文中考虑的是最普通的通信网络系统的情形,对更复杂的多基站多终端组成的通信网络缓存区队长研究具有重要意义.
[1] 赵天驰,邢远.基于马尔科夫链理论的通信网络建模与性能分析[J].电子科学技术,2015,2(6):657-660.
[2] 孙洪祥.随机过程[M].北京:机械工业出版社,2009.
[3] 戴琳,秦叔明,董艳梅.切换排队且排队优先的通信信道配置模型[J].云南师范大学学报,2012,32(2):42-46.
[4] 王亚军,张艳.σ-代数下条件期望的若干应用[J].哈尔滨师范大学自然科学学报,2016,32(3):1-3.
[5] 陈红燕,邓臻.随机变量数学期望计算[J].哈尔滨师范大学自然科学学报,2015,31(5):44-45.
ResearchonDataQueueofCommunicationBufferBasedonBirth-DeathTheory
Wang Yajun, Zhang Yan, Zhou Shengwu, Li Jingyu
(China University of Mining and Technology)
In a communication network, the rate of uplink and downlink of data transmission between base station and terminal is different. Before the data is uploaded successfully, a certain number of packets are stuck at the terminal. This retention area is called the buffer zone. In this paper, the queue length problem of the buffer packets is studied, and the absolute distribution of the queue length and the steady-state solution of the average queue length and the average residence time of the packets are obtained.
Birth death theory; Communication network; Buffer area; Queue length
季春阳)
O211.62;TN911
A
1000-5617(2017)04-0006-03
2017-04-11
*中国矿业大学2017年校教育教学改革立项项目(2017YB28)
