非倍测度下局部Ap权的性质
2018-01-08孙红妍宋福陶
孙红妍, 丰 华,宋福陶
(哈尔滨师范大学)
非倍测度下局部Ap权的性质
孙红妍, 丰 华,宋福陶
(哈尔滨师范大学)
文献[1]介绍了经典Ap权的定义, 随后文献[2]介绍了局部Ap权的定义, 最后在文献[3]-[5]中了解到非倍测度的定义和倍测度下的局部Ap权的很多性质的证明. 给出了可测度量空间中非倍测度下局部Ap权的性质, 并且特别证明了非倍测度下局部Ap权性质是和方体边长的限制常数无关的.
非倍测度; 局部Ap权; 反Hölder不等式
0 引言
1972年, Muckenhoupt[1]在讨论Hardy-Littlewood极大算子有界性时开创了Ap权理论.
定义1[1]设w≥0,w∈Lloc(Rn),1

则称w∈Ap.若存在常数C>0,使得对所有的方体Q都有:

则称w∈A1.
自从Muckenhoupt给出了Ap权定义后, 权理论便得到了广泛的关注, 学者们开始考虑算子在不同空间以及不同测度下的加权有界性, 在讨论奇异积分有界性时曾多次用到一个初等的事实:|2Q|=2n|Q|, 因此为了得到类似的结论, 常常假设μ具有倍测度性质, 即存在常数D,使得对所有的方体Q都有:μ(2Q)≤Dμ(Q).
2010年, Lin和Stempak[2]定义了Rn(n≥1)中的局部Ap权.

定义2[2]设0


在2002年,Orobitg和Pe′rez[3]给出了非倍测度的定义以及在此测度下Ap权的定义和性质. 并且定义了一个d维的Borel测度μ, 使得它不具有倍测度的性质, 即:μ(B(x,r))≤rd,x∈Rn,r>0.
定义3[4]设w是测度空间(Rn,μ)上的非负局部可积函数, 对于0


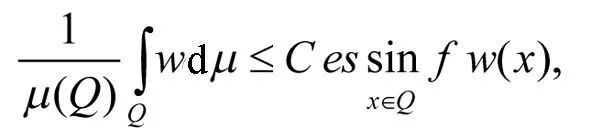



其中C仅与p,k和w的非倍测度下局部k-Ap权常数有关.
1 主要结果







另一方面,









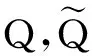



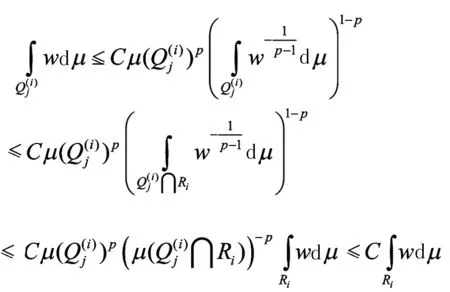
其中C>0.


类似的有

以及










(i)设D=Q∩{x:|f(x)|=0},μ(D)=0,则有:

证明






(e)存在常数C1,C2>0, 使得对∀Q∈Ok有:


(f)存在常数C1,C2>0, 使得对∀Q∈Ok有:
当p=1时, 显然.


因此, 有:


(g)存在常数C1,C2>0, 使得对∀Q∈Ok有:
当p=1时, 由定义可知:

其中M表示非倍测度下H-L极大算子.
当p>1时, 有下列不等式


(h)存在常数C1,C2>0, 使得对∀Q∈Ok有
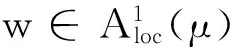


则有
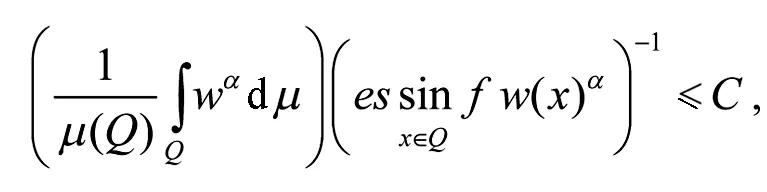



α2>1, 则有

取α=min{α1,α2}, 则有






[1] Muckenhoupt B. Weighted norm inequalities for Hardy maximal function[J]. Trans Amer Math Soc, 1972, 165: 207-226.
[2] Lin C C, Stempak K. Local Hardy-Littlewood maximal operator[J]. Math Ann, 2010,4(348): 797-813.
[3] Orobitg J, Pérez C.Apweights for nondoubling measures inRnand applications[J]. Amer Math Soc, 2002, 5(354): 2013-2033.
[4] 丰华. 非倍测度下的C-Z奇异积分算子在局部权下的有界性[D].哈尔滨师范大学, 2017.
[5] 鞠娜, 陈建仁.Rd(d≥1)上局部Ap权的性质与反Hölder不等式[J]. 哈尔滨师范大学自然科学学报,2011,27(3):27.
ThePropertiesofLocalApWeightsonNondoublingMeasures
Sun Hongyan, Feng Hua, Song Futao
(Harbin Normal University)
In this paper, the definition of classicalAprights was introduced through literature[1], then the definition of localAprights was introduced through literature[2]. In the end, the definition of non-double measure and the many properties of localAprights under the double measure were proved. Therefore, the property of the partial power of the measurable measurement space was given, and the localApproperty of the non-double measure is independent of the limit constant of the side length of the square were proved.
Nondoubling measures; LocalApweights; Reverse Hölder ineguality
于达)
O174.12
A
1000-5617(2017)04-0009-05
2017-05-04
