结合纹理去除的遥感图像分割

周明非，汪西莉

(陕西师范大学 计算机科学学院，西安 710119)

结合纹理去除的遥感图像分割

周明非，汪西莉*

(陕西师范大学 计算机科学学院，西安 710119)

针对包含复杂纹理信息的遥感图像难以进行精准图像分割的问题，提出了一种结合纹理去除的遥感图像分割方法。首先，改进了相对全变差纹理去除方法,通过引入新的范数约束使相对全变差纹理去除方法可以在去除纹理信息的同时凸显图像中的主要结构，达到辅助分割的效果；然后，使用均值漂移算法对经过纹理去除的遥感图像进行无监督聚类，达到分割的目的；最后，提出的遥感图像分割算法在不同遥感图像上进行了测试。实验结果表明，在高分辨遥感图像的分割上，所提算法可以分割出遥感图像中的主要目标，和直接分割或者结合其他纹理去除方法相比取得了更好的分割结果。所提出的分割算法可以降低纹理信息对图像分割的影响，提高遥感图像分割的精度。

纹理；相对全变差；均值漂移；遥感图像分割

0 引言

遥感图像分割指的是把遥感图像中的主要目标(如房屋、道路、农田等)分割出来，为进一步的图像分类和目标检测做好准备。在高分辨遥感图像的分割上，由于大量纹理信息的存在，目标可能较小，精准的图像分割变得十分困难[1-2]。目前比较流行的遥感图像分割方法主要有多阈值分割[3]、拓扑无监督学习[4]、模糊聚类[5]、遗传算法[6]以及活动轮廓[7]等。但是上述方法都没有考虑纹理信息对图像分割的影响。如何抑制图像中的纹理信息并得到精准的遥感图像分割轮廓，成为一个具有挑战性的课题。

2011年，Xu等[8]提出了L0平滑方法实现图像纹理信息的去除。L0平滑方法是指在处理图像时引入全局性的稀疏性约束，通过控制整幅图像中的非零梯度的数量来达到凸显图像中的主要边缘并抑制部分低振幅纹理和噪声的效果[9-10]。但是这种L0平滑方法并不能处理图像中的大区域或者高振幅的纹理信息和噪声，直接用L0平滑方法辅助遥感图像的分割并不能得到理想的效果。2012年，Xu等[11]在全变差理论的基础上[12-15]提出了基于相对全变差(Relative Total Variation, RTV)的纹理去除方法。使用相对全变差方法进行纹理去除时，既能保留图像中的主要结构，又能去除纹理信息的影响[16]。和双边滤波[17]以及加权最小二乘法[18]相比，相对全变差方法取得了更好的纹理去除效果。2016年，Liu等[19]改进了相对全变差方法，通过改变相对全变差方法中窗口全变差和窗口固有变差的定义，得到了较好的纹理去除效果。但是由于高分辨遥感图像中存在大量纹理信息并且主要结构目标和纹理杂糅在一起，使用相对全变差方法处理高分辨遥感图像时会带来图像的过度平滑并模糊主体结构边缘，不利于辅助图像分割。

本文提出了一种结合纹理去除的遥感图像分割方法，改进体现在三个方面: 首先，纹理信息的存在会阻碍遥感图像的分割，本文把纹理去除方法引入到了高分辨遥感图像的分割中，和直接分割相比提升了遥感图像的分割效果; 其次，本文提出了一个针对相对全变差方法的改进方案，把相对全变差方法中图像相似性约束项的L2范数改为L1范数, 通过引入L1范数，可以使得相对全变差方法在平滑纹理信息的同时更好地保留图像主体结构，从而避免过度平滑并辅助分割; 再次，提出的新的遥感图像分割方案中，遥感图像首先使用基于L1范数的相对全变差方法进行纹理信息的去除，然后使用均值漂移(Mean Shift)算法[20]进行图像分割。实验结果表明，使用基于L1范数的纹理去除方法进行图像预处理之后，遥感图像中的主要目标会被凸显出来，此时使用均值漂移算法对遥感图像进行分割可以得到更高的分割精度和更清晰的分割边缘。

1 相对全变差与均值漂移算法

本章首先介绍相对全变差方法与均值漂移算法的基本原理。

1.1 相对全变差纹理去除方法

相对全变差方法通过对图像求解一个全局目标函数来达到纹理去除的效果。相对全变差方法构造的目标函数如式(1)所示：

(1)

以两个维度的灰度图为例，式(1)中的O表示目标图像，即算法的输出图像；I表示输入图像；p表示二维图像中的像素。式(1)中的项(O-I)2表示目标函数中的使用L2范数的图像相似性约束项。图像相似性约束项之后是相对全变差正则项，其中，k是一个权重系数，代表目标函数中相对全变差正则项所占的比重。τ是一个很小的正数，设置τ是为了避免分母为0的情形发生。相对全变差正则项有两个重要组成部分，分别是窗口全变差(Windowed Total Variation, WTV)和窗口固有变差(Windowed Inherent Variation, WIV)。x方向和y方向的窗口全变差对应于式(1)中的Dx(p)和Dy(p)，x方向和y方向的窗口固有变差对应于式(1)中的Lx(p)和Ly(p)。其中，x方向和y方向的窗口全变差的定义如式(2)和式(3)所示:

(2)

(3)

其中：q∈U(p)表示像素点q属于一个以像素点p为中心的四方形邻域中；∂x和∂y表示二维图像中的像素在x和y两个方向上的偏导数。gp,q是一个权重系数，其定义为:

(4)

其中σ控制正则项中的空间尺度。x方向和y方向的窗口固有变差的定义如式(5)和式(6)所示:

(5)

(6)

含有大量纹理信息的窗口区域和含有主要结构边缘的窗口区域相比有较小的窗口固有变差值，这就使得窗口固有变差成为保留图像主要结构并去除纹理信息的关键。另外，窗口全变差衡量的是图像区域中结构的强度和显著性，引入窗口全变差可以强化图像中的主要结构。因此，使用相对全变差方法去除纹理时图像纹理和主要结构具有了可分性，从而避免了图像纹理信息和主要结构信息在进行优化时受到同等惩罚的情况，得到了较好的纹理去除效果。

但是，遥感图像中目标较小，且目标和纹理信息往往杂糅在一起，使用相对全变差方法时会产生过度平滑并模糊主要目标边缘，不利于下一步的图像分割。关于相对全变差方法的改进在第2章阐述。

1.2 均值漂移图像分割算法

在处理高分辨遥感图像的分割时，由于图像的规模和信息量十分巨大，直接使用均值漂移算法进行分割的计算消耗就变得十分巨大。本文使用的均值漂移算法是Paris等[20]对经典的均值漂移算法的一种改进。通过引入拓扑学的相关知识，均值漂移算法可以更加高效地提取特征空间中的密集点，大幅降低了均值漂移图像聚类所消耗的时间，提高了图像分割的效率。经测试，使用Paris等[20]的方法进行大幅遥感图像分割和使用经典均值漂移算法相比速度提高3～6倍。

Paris等[20]提出的均值漂移算法主要包含3个参数，分别是尺度因子σsc、空间因子σsp和阈值τthr。其中，尺度因子和空间因子分别代表进行分割时算法在颜色空间和X、Y轴上的选择尺度。尺度因子和空间因子的值越小，初始聚类越多，分割越细致，但是内存消耗越大。尺度因子和空间因子越大，分割越简略，内存消耗变少。而阈值τthr是衡量两个聚类区域是否需要合并的标准。一般情况下，过小的阈值设定会带来更多的聚类和冗余的分割边界，本应该被分为一类的目标有可能被分开；而如果使用过大的阈值设定，很多本应该被分开的目标会被合并在一起。

2 L1范数的相对全变差纹理去除方法

在高分辨遥感图像的分割中，使用相对全变差方法时无法显著区分较为相似的纹理信息和图像主要结构的边界，从而导致图像的过度平滑，遥感图像中的一些主要目标将不会被检测出来，从而降低图像分割的精度。

针对以上问题，本文提出的解决思路是在相对全变差纹理去除方法中引入L1范数。从Liu等[19]的证明中可以得出结论，和L2范数相比，L1范数可以保护全局不同目标之间的对比度并减小纹理去除方法对图像异常值的敏感度，使用L1范数更能保护图像中的主要结构信息。改进后的方法可以强化图像中的主要结构，并提升图像不同目标之间的对比度，这对进一步的分割来说是十分重要的。结合L1范数的相对全变差方法的目标函数如式(7)所示：

(7)

和相对全变差方法的目标函数相比，式(7)的不同之处在于图像相似性约束项改为使用L1范数。改进后的方法中的窗口全变差和窗口固有变差的定义均和相对全变差方法相同；同时，范数的改变使得目标函数求解计算变得方便。

式(7)所表示的目标函数是非凸的。由于带有平方项的目标函数也可以被线性地优化，相对全变差正则项可以被分解成一个非线性项和一个平方项来处理。由于其中的非线性项又可以转化为一系列的线性优化问题来求解，这就找到了一种高效求解目标函数的方式。根据Xu等[11]的陈述，在x坐标方向上，相对全变差正则项可以按照式(8)的方式进行分解。

(8)

式(8)可以近似为式(9)：

(9)

进一步简化得到式(10):

(10)

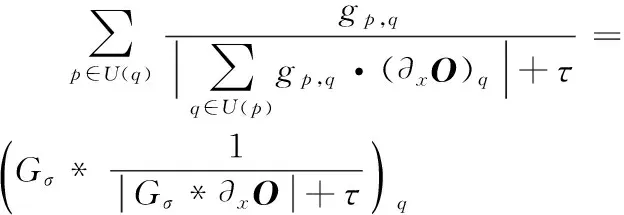
(11)

(12)

式(11)中:Gσ是一个标准差为σ的高斯过滤器。运算符*指卷积运算。式(12)中，τs是一个防止分母为0的小正数。同样的，在y坐标方向上，可以对相对全变差正则项作式(13)所示的分解。

(13)

式(13)中同样包含两个非线性项和一个平方项。平方项是y坐标方向上偏导数的平方，两个非线性项的定义分别如式(14)和式(15)所示:

(14)

(15)

上述分解有助于把全变差正则项转变为矩阵形式。为了把目标函数全部转化为矩阵形式，需要对式(7)中的L1范数作一些变形。根据Liu等[19]的表述，L1范数和L2范数之间存在相关性，可以对L1范数作式(16)所示的变换。

(16)

经过上述变换，目标函数可以被变换成式(17)所示的形式:

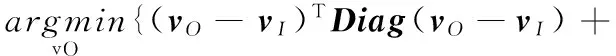
k·(vOTCxTUxWxCxvO+vOTCyTUyWyCyvO)}

(17)

式(17)中，Diag是一个对角矩阵，其对角值如式(18)所示:

(18)

式(18)表示，对角矩阵Diag的对角值为1除以矩阵O和矩阵I的对应元素差值加上一个很小的正数。式(17)中，vO代表目标图像O的向量表示，vI代表输入图像I的向量表示。Cx和Cy是由离散梯度算子得到的Toeplitz矩阵。Ux、Uy、Wx和Wy是对角矩阵，其对角值分别为：Ux[i,i]=ux,i，Uy[i,i]=uy,i，Wx[i,i]=wx,i，Wy[i,i]=wy,i。

式(17)可以使用一个快速迭代优化过程进行求解。迭代求解过程分为两个步骤。首先，使用上一次迭代计算得到的当前目标图像O，根据式(11)、式(12)、式(14)和式(15)计算ux,q、wx,q、uy,q和wy,q，并进一步计算出Ux、Wx、Uy和Wy。然后，使用计算到的值求解一个线性优化问题，求解公式如式(19)所示：

(19)

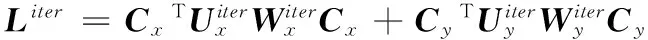
图1中给出了L1范数的相对全变差纹理去除方法的纹理去除结果和相对全变差纹理去除结果的对比。图1中的差异图是L1范数的相对全变差纹理去除方法的纹理去除结果减去相对全变差纹理去除结果得到的差异图，差异图进行了二值化来突出差异部分。图1中差异图的黑色部分是两种平滑结果相同的部分，白色部分是结果图中使用L1范数的相对全变差方法和相对全变差方法相比增强的部分。从差异图中可以看出，L1范数的相对全变差方法可以增强目标和背景的对比度，并强化主要目标的边缘。

图1 两种方法纹理去除结果对比Fig. 1 Comparison of texture removal results by using two methods

3 参数分析

L1范数的相对全变差纹理去除方法主要有两个可调参数，分别是权重k和尺度σ。其中，权重k指的是式(7)中的权重系数，衡量图像相似性约束项和相对全变差正则项之间的权重，其取值一般在0.001～0.1。尺度σ指的是式(4)中的窗口全变差和窗口固有变差的窗口大小。σ的取值和图像本身的性质有关。包含大纹理的图像应该使用大的σ取值进行平滑；相反的，如果图像只包含小结构的纹理，应选取小的σ取值，σ的取值一般在0.1～10。

参数σ相同的情况下，参数k对图像纹理去除效果的影响如图2所示。

图2 参数k对图像纹理去除效果的影响(σ=4)Fig. 2 Effects of the parameter k to the image texture removal results (σ=4)

从图2中可以看出，σ不变时，k的取值越大，图像被平滑的程度越高，纹理去除效果越好，但是对图像主体结构的破坏也就越大; 反之，k的取值越小，纹理去除效果越差。只有选取恰当的k值，才能在保护图像主要结构的前提下最大限度地去除纹理信息。图2中，取k=0.001时，很多对图像分割有影响的纹理信息没有被去掉。k=0.025时，图像被过度平滑，不同目标被杂糅在一起。经过实验，最好的参数组合是k=0.005，σ=4。参数k相同的情况下，参数σ对图像纹理去除效果的影响如图3所示。

图3 参数σ对图像纹理去除效果的影响(k=0.004)Fig. 3 Effects of the parameter σ to the image texture removal results(k=0.004)

从图3中可以看出，σ的取值越大，图像越模糊，边缘越不清晰，相比之下，小的σ取值有边缘锐化的作用。在实际应用中，需要参照图像中纹理的结构大小来确定参数σ的取值，过小的σ取值达不到纹理去除的效果，而过大的σ取值会破坏图像中主要成分的结构。图3中，取σ=0.2时，有残余的纹理信息没有去除；而取σ=8时，由于参数σ的取值过大，道路的边界因为过度平滑变得模糊。经过实验，图3中k=0.004，σ=2是最佳的参数组合。

图像经过纹理去除之后直接使用均值漂移算法进行图像分割，得到最终分割结果和分割边缘。由于在分割之前去除了纹理信息，使用均值漂移算法得到的分割结果要优于直接分割得到的分割结果。

4 实验结果

文章实验的主要硬件环境为Intel Xeon CPU E5-2690 v3和256 GB内存，软件环境为64位Ubuntu 14.04系统，实验代码包括Matlab代码和C++代码。实验使用两幅图像，均来自Google Earth截图，图像的大小为800×600。实验图像首先使用结合L1范数的相对全变差方法进行纹理去除，之后使用均值漂移算法[20]进行图像分割。

实验图像有5个对照组，分别是不使用纹理去除、使用双边滤波[17]进行纹理去除、使用加权最小二乘法[18]进行纹理去除、使用L0平滑[8]进行纹理去除和使用相对全变差方法[11]进行纹理去除。所有对照组均使用均值漂移算法[20]进行图像分割。

在进行纹理去除时，实验方法和对照方法的所有参数均人为调到最优，进行图像分割时，同一幅图像的实验中对使用不同纹理去除方法得到的结果固定使用相同的图像分割参数。第一幅图像的实验结果如图4所示，第二幅图像的实验结果如图5所示。

图4 不同方法分割结果对比(一)Fig. 4 Comparison of the segmentation results by different algorithms (Ⅰ)

从图4和图5中可以看出，如果直接使用均值漂移算法进行遥感图像的分割，大量的纹理细节信息会给分割造成很大的影响。直接分割无法产生光滑的分割线，而且会把大量纹理细节错分成遥感目标。这是因为遥感图像本身具有复杂的目标和背景信息，这些信息导致遥感图像中的目标和背景在空间位置和颜色信息两方面都难以区分。比较显著的纹理信息会给分割带来困难，进而造成分割边缘的不平滑和分割结果的不精确。使用双边滤波器进行平滑之后，虽然纹理信息得到了抑制，但是遥感图像中的主要目标也被平滑，导致分割线不完整。使用加权最小二乘法进行图像平滑时，主要轮廓信息会被保留，但是会平滑部分目标主体结构，损失不够明显的主体结构的信息，从而产生了不完整的分割线。图4中，加权最小二乘法可以平滑掉大部分纹理信息，但是立交桥的边缘也被模糊，达不到精确的分割结果。图5中，使用加权最小二乘法时平滑掉了纹理信息，但是由于过度平滑导致对河流和农田的分割结果不够精细。

图5 不同方法图像分割结果对比(二)Fig. 5 Comparison of the segmentation results by different algorithms (Ⅱ)

L0平滑方法趋向于保留图像中的比较显著的边缘，即使这些边缘属于纹理信息; 因此使用L0平滑时，图像中的强边缘会被保留，但是主体目标中不够突出的部分会被忽略，进而产生错分的结果。另外，部分属于纹理信息的显著边缘会被保留，进而产生不精确的分割结果。相对全变差方法可以达到纹理去除和保护主体结构之间的平衡，在普通光学图像的纹理去除方面得到了很好的结果。但是遥感图像中目标和背景更加复杂，且目标和背景之间的差异更加不明显。因此使用相对全变差方法进行纹理去除时，纹理会被较好地去除，但是会产生对主体结构的过度平滑，从而得不到满意的分割结果。

结合L1范数的相对全变差方法充分考虑了遥感图像本身的特点。使用结合L1范数的相对全变差方法进行纹理去除时，图像中的纹理信息会被平滑，同时，图像中的主体目标部分会被加强。此时使用均值漂移算法进行图像分割，得到了最好的分割结果。本文方法得到的分割边缘光滑且清晰，主体目标和背景得到了很好的区分，另外，主体结构的细节部分也被保留，得到了最完整的分割线。图4和图5同时表明和对比方法相比，本文方法可以处理并更加适用于高分辨遥感图像的纹理去除和图像分割。

5 结语

本文提出了一种新的高分辨遥感图像分割方法，在进行分割之前，首先使用结合L1范数的相对全变差方法进行遥感图像的纹理去除。和其他纹理去除方法相比，结合L1范数的相对全变差方法拥有最好的性能，既拥有强大的纹理去除能力，又不会过度平滑图像的主要结构，去除纹理之后的图像中的主要结构被加强。经过纹理去除之后的图像使用均值漂移算法进行图像分割，得到的分割结果和直接分割或者使用其他纹理去除方法相比可以得到更加准确的分割结果和更光滑的分割边缘。

图像分割是为了进一步的图像分类和目标检测做准备，未来的工作重点将是使用本文方法进行遥感图像分割并辅助高分辨遥感图像的分类和目标检测。有了高效的遥感图像分割算法作为辅助，遥感图像分类和目标检测的精度将会有所提高。另外，本文方法也可以被应用到基于卷积神经网络的遥感图像分割中。

References)

[1] YUAN Q, ZHANG L, SHEN H. Hyperspectral image denoising employing a spectral-spatial adaptive total variation model[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(10): 3660-3677.

[2] 郭玲玲, 张立国, 吴泽鹏,等. 基于受限全变差正则化的遥感图像去模糊方法[J]. 激光与光电子学进展, 2013, 50(11):88-93.(GUO L L, ZHANG L G, WU Z P, et al. Deblurring of remote sensing images based on constrained total-variation regularization[J]. Laser & Optoelectronics Progress, 2013, 50(11):88-93.)

[3] MUANGKOTE N, SUNAT K, CHIEWCHANWATTANA S. Multilevel thresholding for satellite image segmentation with moth-flame based optimization[C]// JCSSE 2016: Proceedings of the 2016 International Joint Conference on Computer Science and Software Engineering. Piscataway, NJ: IEEE, 2016: 1-6.

[4] GROZAVU N, ROGOVSCHI N, CABANES G, et al. VHR satellite image segmentation based on topological unsupervised learning[C]// Proceedings of the 14th IAPR Conference on Machine Vision Applications. Piscataway, NJ: IEEE, 2015: 543-546.

[5] GANESAN P, PALANIVEL K, SATHISH B S, et al. Performance of fuzzy based clustering algorithms for the segmentation of satellite images — a comparative study[C]// Proceedings of the 2015 IEEE Seventh National Conference on Computing, Communication and Information Systems. Piscataway, NJ: IEEE, 2015: 23-27.

[6] PARE S, BHANDARI A K, KUMAR A, et al. Satellite image segmentation based on different objective functions using genetic algorithm: a comparative study[C]// Proceedings of the 2015 IEEE International Conference on Digital Signal Processing. Piscataway, NJ: IEEE, 2015: 730-734.

[7] DEEPIKA N P, VISHNU K. Different techniques for satellite image segmentation[C]// Proceedings of the 2015 Online International Conference on Green Engineering and Technologies. Piscataway, NJ: IEEE, 2015: 1-6.

[8] XU L, LU C, XN Y, et al. Image smoothing via L0 gradient minimization[J]. ACM Transactions on Graphics, 2011, 30(6):61-64.

[9] SHEN C T, CHANG F J, HUNG Y P, et al. Edge-preserving image decomposition using L1 fidelity with L0 gradient[C]// SIGGRAPH Asia 2012 Technical Briefs. New York: ACM, 2012: Article No. 6.

[10] CHENG X, ZENG M, LIU X. Feature-preserving filtering with L0 gradient minimization[J]. Computers & Graphics, 2014, 38(1):150-157.

[11] XU L, YAN Q, XIA Y, et al. Structure extraction from texture via relative total variation[J]. ACM Transactions on Graphics, 2012, 31(6): 439-445.

[12] RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica D: Nonlinear Phenomena, 1992, 60(1/2/3/4): 259-268.

[13] OLIVEIRA J P, BIOUCAS-DIAS J M, FIGUEIREDO M A T. Adaptive total variation image deblurring: a majorization-minimization approach[J]. Signal Processing, 2009, 89(9): 1683-1693.

[14] 吴晓旭, 刘秀平, 刘宇,等. 局部加权全变差下的盲去模糊[J]. 计算机辅助设计与图形学学报, 2014, 26(12):2173-2181.(WU X X, LIU X P, LIU Y, et al. Blind deblurring based on local weighted total variation[J]. Journal of Computer-Aided Design and Computer Graphics, 2014, 26(12):2173-2181.)

[15] 万洪林, 彭玉华, 曲怀敬. 全变差数字滤波器与Ridgelet变换相结合的图像去噪方法[J]. 电子学报, 2008, 36(1):90-94.(WAN H L, PENG Y H, QU H J. Image denoising method with combination of digital TV filter and Ridgelet transform[J]. Acta Electronica Sinica, 2008, 36(1):90-94.)

[16] WU H, TU S, WANG L, et al. Video Texture Smoothing based on Relative Total Variation and Optical Flow Matching[M]. Berlin: Springer, 2014:13-21.

[17] PARIS S, DURAND, F. A fast approximation of the bilateral filter using a signal processing approach[J]. International Journal of Computer Vision, 2009, 81(1):24-52.

[18] FARBMAN Z, FATTAL R, LISCHINSKI D. Edge-preserving decompositions for multi-scale tone and detail manipulation[J]. ACM Transactions on Graphics, 2008, 27(3):15-19.

[19] LIU Q, XIONG B, YANG D, et al. A generalized relative total variation method for image smoothing[J]. Multimedia Tools and Applications, 2016, 75(13):7909-7930.

[20] PARIS S, DURAND F. A topological approach to hierarchical segmentation using mean shift[C]// Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2007:1-8.

This work is partially supported by the National Natural Science Foundation of China (41171338，41471280，61401265).

ZHOUMingfei, born in 1993, M. S. candidate. His research interests include remote sensing image processing, pattern recognition.

WANGXili, born in 1969, Ph. D., professor. Her research interests include intelligent information processing, image perception and comprehension.

Remotesensingimagesegmentationwithtextureremoval

ZHOU Mingfei, WANG Xili*

(SchoolofComputerScience,ShaanxiNormalUniversity,Xi’anShaanxi710119,China)

Focused on the issue that the precise segmentation of remote sensing images which contain complex textures is always difficult, a novel algorithm which combined remote sensing image segmentation with texture removal was proposed. Firstly, the method of texture removal with relative total variation was improved. A new norm constraint was introduced to the relative total variation algorithm, which helped to enhance the major structures in images while removing textures. Meanwhile, the improved texture removal method could assist the following image segmentation. Secondly, mean shift algorithm was used to segment remote sensing images after texture removal by unsupervised clustering. The proposed segmentation algorithm of remote sensing images was tested on different remote sensing images. The experimental results demonstrate that the proposed method can split the main objects from very high resolution remote sensing images. The proposed method obtains better results compared with other methods of remote sensing image segmentation which segmented images without texture removal or segmented remote sensing images combined with other texture removal methods. The proposed method can reduce the influence of texture on image segmentation and improve the accuracy of remote sensing image segmentation.

texture; relative total variation; mean shift; remote sensing image segmentation

2017- 05- 16;

2017- 06- 15。

国家自然科学基金资助项目(41171338, 41471280, 61401265)。

周明非(1993—)，男，山东济宁人，硕士研究生，主要研究方向：遥感图像处理、模式识别； 汪西莉(1969—)，女，陕西西安人，教授，博士，CCF高级会员，主要研究方向：智能信息处理、图像感知与理解。

1001- 9081(2017)11- 3162- 06

10.11772/j.issn.1001- 9081.2017.11.3162

(*通信作者电子邮箱learning527@126.com)

TP751.1

A