基于置信传播的复杂网络社团发现算法

尤心心，葛 檬

(天津大学 软件学院，天津 300350)

基于置信传播的复杂网络社团发现算法

尤心心，葛 檬*

(天津大学 软件学院，天津 300350)

经典的置信传播(BP)算法能够通过有限次数的迭代，推断出所有节点的边缘概率分布和最大似然概率。针对该算法在迭代过程中产生的影响精度和收敛速度的强烈震荡，找出了造成震荡的三个主要因素：强势能、紧密的环路和矛盾的方向，并有针对性地改进了该算法的核心更新规则；同时又进一步提出了异步消息传递方式，克服传统置信传播算法采用的同步消息传播方式的收敛慢、效率低等缺点。利用随机块模型拟合网络的生成过程，利用经典的期望最大化算法对模型进行求解，分别利用改进前后的置信传播算法推断隐变量的后验概率。在五个真实网络上的实验表明，两个改进均使得精度和速度不同程度地提高。

复杂网络；社团发现；置信传播；随机块模型；收敛速度

0 引言

社团结构是复杂网络[1]的一个重要特征，它将网络分成具有密集内在联系的子群，同一社团中的节点通常拥有共同的性质和紧密的关系[2]。因此，社团发现[3]问题成为了复杂网络研究中的一个重要的热点问题，激发了大量来自不同领域的学者对其进行研究。从社团发现算法的研究内容方面，可分为：1)基于网络结构的社团发现，代表方法有：凝聚或分裂算法[4]、基于模块度优化的方法[5]、谱方法[6]、动力学方法[2]、基于标签传播的方法[7]、基于仿生算法的方法[8]；2)基于随机模型的社团发现[9-11]等。随机模型被视为一类非常有前景的方法[12]，其大部分都是通过拓展或改进随机块模型[13]对社团结构进行描述，并通过定义不同类型的目标函数、采用不同优化算法来推导出社团结构。本文利用随机块模型拟合网络的生成过程，使用经典的期望最大化算法进行优化[10-11]，期望部分的目标是推理隐变量的后验概率，本文利用置信传播算法[14]承担这一关键任务，该算法能够通过有限次数的迭代，推论出节点的边缘概率分布和最大似然概率；最大化部分是利用通过期望部分得到的隐变量的后验概率计算模型参数。通过期望和最大化两个步骤的多次迭代达到收敛，收敛后每个节点的边缘概率分布中最大的值对应的社团被认为是该节点的社团标签，随机块模型的参数也得到确定。

然而，在置信传播算法迭代过程中，往往会不断发生震荡的现象，如图1所示，虚线呈现出非常强烈的震荡，并且一直没能收敛，而实线经过几次迭代很快就收敛了，这说明震荡会导致收敛速度慢，进而影响精度。很显然，本文希望尽量避免这样的震荡，也就是在图中只出现这种快速收敛的实线。经过大量理论研究，本文总结产生震荡的原因有3个：一是强烈的势能，也就是不同节点对之间的势能差值非常大；二是紧环，也就是节点之间形成环的紧密程度；三是矛盾的方向。这三点组合在一起，势能差值越大，环越紧，方向矛盾程度越强烈，震荡越激烈。

其次，置信传播算法每次迭代收敛的消息数量太少，这也将会导致速度和精度同时变差。这主要是因为大多数置信传播算法在迭代过程中采用的是同步更新，如图2(a)所示，每一次更新意味着所有节点同时计算即将发出的消息并将其发出，所有节点也同时收到所有其他节点发来的消息，也就是说每个节点第一次发出的消息只是它自身携带的信息，并不能结合其他节点发来的消息一并发送出去，这样的消息内容显然不够充分。如果从便于实现的角度来说，这是一个不错的算法，可以实现平行的工作，彼此之间没有任何依赖。但不幸的是，同步置信传播算法每次迭代传递的消息中包含的有价值信息太少，这导致每次迭代收敛的消息数目比较少，收敛速度也非常慢。

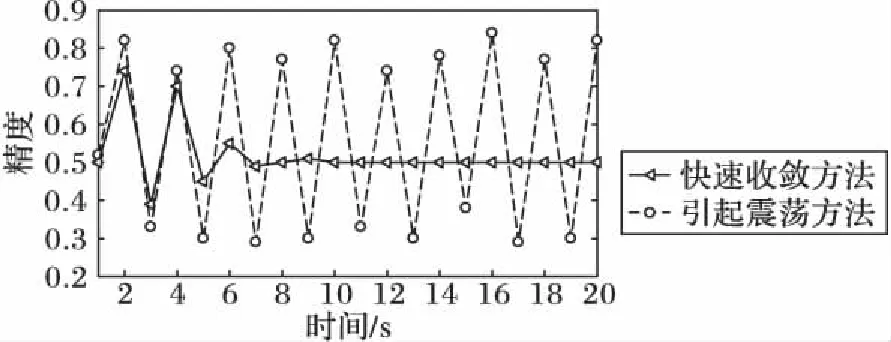
图1 震荡与收敛对比Fig. 1 Comparison of oscillation and convergence

图2 同步与异步更新对比Fig. 2 Comparison of synchronous and asynchronous updates

为了解决震荡问题，本文提出这样的改进措施：在每次计算消息时，采取一个权重的方式加入旧的消息，也就是说一条新消息等于一定比例的旧消息(上次迭代计算出的信息)加上一定比例的新消息(本次迭代计算出的消息)，并且通过控制权重参数平衡新、旧消息产生的影响，这样能有效减小势能的强烈差异和方向上的矛盾程度，同时也能缓解紧环的现象，大幅减弱甚至消除震荡。针对第二个问题，本文提出针对同步消息传递方式缺点改进后的异步消息传递方式，即每次只更新一条消息，下一条需要被更新的消息能够综合发送方自身的信息和其他节点发来的新消息，这样每条消息携带的信息既丰富又新鲜，每次的消息传递效率也更高。如图2(b)所示，第一条消息是1号节点将自身的信息发送到2号节点；第三条消息是2号节点将自身的信息和1号节点发来的新消息进行综合之后，再发送到3号节点。采用这样的消息传递方式能够使得每一条新更新的消息(例如1号节点发给2号节点的消息)立即投入使用，所以每次迭代过后收敛的消息数量会大幅增多，速度和精度都得到提高。

1 方法

1.1 问题描述

假设现在有一个观测到的随机图[15]，其具有n个节点和m条边，这个图用对称邻接矩阵A来表示，如果节点u和节点v之间有边，A中对应位置auv=1；否则，auv=0。现在的目标是划分这n个节点到K个社团中，使用随机块模型刻画网络的生成过程[16]，假设邻接矩阵中每一项auv都是独立的且服从泊松分布的；每一个节点u具有一个社团标签Gu∈{1，2，…，K}，表示节点u所在的社团，且Gu～Multi(γ)；块分配是所有Gu的集合。假设块之间的边个数服从泊松分布，这些泊松分布通过一个K×K的块关联矩阵ω被指定。

取对数的完全数据似然公式是：

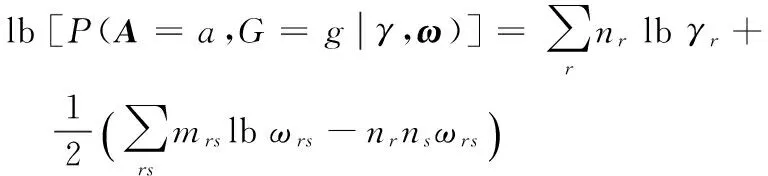
(1)

这里nr是块r中节点数，mrs是连接块r和块s的边的数量。参数γ和ω可以通过最大化式(1)给出：

现在的目标是通过联合在γ、ω和g上最大化式(1)，从而确定块分配G；如果用统计物理专业的术语来表达，就是去发现基态g，基态g能够最小化-lb [P(a,g|γ,ω)]的能量。为了得到参数γ和ω，关注生成图的总似然函数：

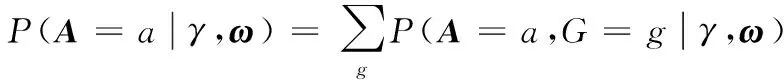
(2)

对所有K×n个可能的块分配进行加和。

本文使用期望最大化算法对模型进行求解，利用置信传播算法估计包括对数似然-lb [P(a,g|γ,ω)]和每个节点的边缘化分布，也就是期望步骤的求解目标，但置信传播算法存在严重的震荡问题，并且同步消息传递方式带来的结果并不令人满意，所以本文要针对这两点问题提出改进。

1.2 震荡减弱

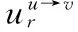
(3)

代表如果Gu=r，Gr=s时auv采取它观测值的概率。那么有：

(4)

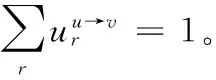
如果直接利用式(4)传递消息，就会产生强烈的震荡，这是因为每个从节点u发送到节点v的新消息都是节点u“综合”自己的信息和其他节点发来的消息而成的，这可能造成新消息和旧消息之间势能差值非常大，例如：u和v这对节点的势能值是100，而v和w这对节点的势能值仅仅是2；或者形成紧环，在消息传递过程中，当然不希望传递顺序太快形成环路，因为这意味着每个节点能收集到的消息非常少，容易造成自我增强，环越紧代表环路上包含的节点越少，传递的消息越来越失去价值；又或者是方向上的矛盾，例如：在随机选择更新顺序的情况下，假设节点在本次迭代中是按照顺时针方向传递消息，这个方向趋于让两个节点具有相同的值，但下次迭代的顺序又是随机选择的，可能恰好让这两个节点按照逆时针顺序传递消息，这个方向又趋于让两个节点具有不相同的值，这就造成了方向上的矛盾。这三种情况中的任何一种，都会使得震荡发生，从而导致收敛过慢、精度下降等不好的现象。

为了避免震荡的发生，本文针对上面提到的三个导致震荡的原因提出了改进，即每次传递消息时，采取权重的方式加入旧消息，也就是说一条新消息等于一定比例的旧消息加上一定比例的新消息，利用公式表达：

(5)

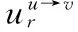
在进行消息传递时，有两种传递方式：一种是同步，一种是异步。同步更新方式的问题在于每次迭代使用的值都是上一次整体迭代之后的结果值，在新一轮迭代中，先计算出的“消息”值没有立即得到使用，而是一直延迟到本轮迭代之后下一轮才投入使用，所以收敛速度非常地慢，每次收敛的消息数也比较少。

那么相反，考虑异步置信传播算法，针对同步方式存在的问题，在异步迭代方式中，先计算出的消息立即投入使用，也就是说每次只计算一条消息，下一条需要被计算的消息能够立即使用刚刚计算出的所有新的消息，这样一次迭代使用的所有消息都是目前能得到的最新消息，每条消息所携带的信息非常丰富和及时，使得收敛速度变快，并且收敛的消息数量也会增多。

2 实验

为了验证提出方法的有效性，本文分别在5个真实网络上进行了实验，关于网络的详细数据见表1。本文采用兰德指数(Rand Index, RI)[18]和归一化互信息(Normalized Mutual Information, NMI)[19]这两个指标对实验结果进行评价。

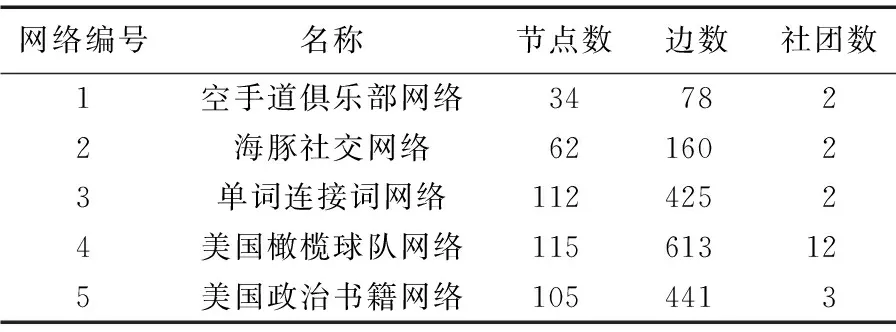
表1 数据集介绍Tab. 1 Introduction of datasets

2.1 实验一

实验一针对解决震荡问题提出的改进，所以都采用同步消息传递方式。实验方法是控制λ的范围从0～0.9，每次增加0.1，例如：λ=0.6表示60%的旧消息加上40%的新消息；λ=0代表没有改进。λ的值不能取1，因为取1表示完全都是上次迭代的消息，这本身没有意义。这里设置λ=0.5，原因可见后面的2.3节参数分析。实验结果见表2。很明显，改进后的算法无论是在速度上还是精度上都呈现出了更好的结果，这说明本文对于产生震荡问题的原因总结得比较好，采取的改进公式也起到了相当好的作用。

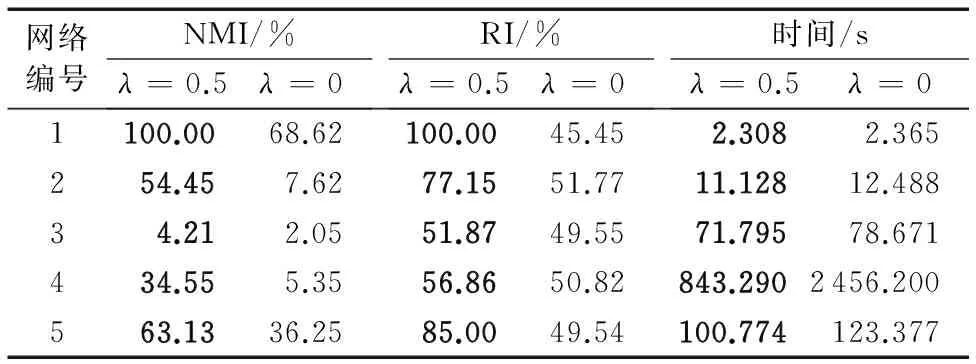
表2 不同λ值时，改进算法性能Tab. 2 Improved algorithm performance under differfent λ

2.2 实验二

实验二针对第二点改进，也就是异步同步对比实验，控制λ=0。异步或者是同步针对的都是置信传播算法中的消息传递方式来说的，从理论上讲，这两种不同的消息传递方式会影响算法的收敛速度和精度，并且异步置信传播算法在多数情况下应该优于同步置信传播算法。实验结果见表3。

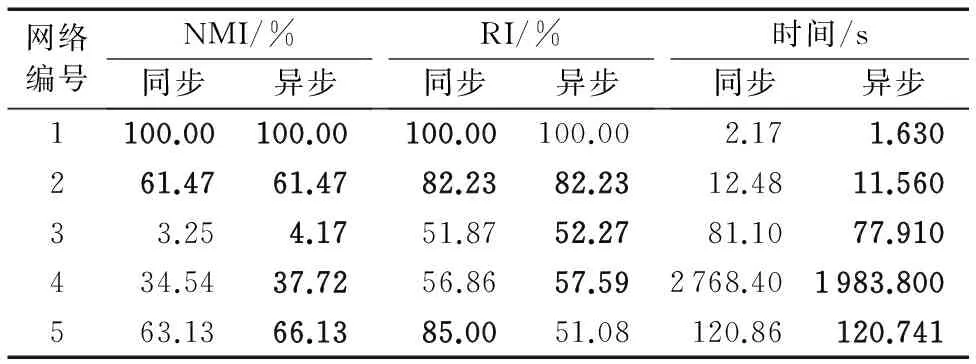
表3 采用同步异步更新时算法性能Tab. 3 Performace with synchronous vs asynchronous update ways

2.3 参数分析

实验测试了参数λ对于网络的影响，正如之前提到的，λ的取值从0～0.9，每次增加0.1，这里忽略λ=0的情况，因为其代表没有改进，和参数分析无关。由于不同网络趋于展现出相同的结果趋势图，所以这里选取3个网络(空手道俱乐部网络、海豚社交网络和单词连接词网络)为代表。对于这3个网络本文分别使用归一化互信息(NMI)和兰德指数(RI)两种评价指标。如图3(a)所示，在λ取值为0.2～0.6，精度没有发生变化，结果曲线表现得完全稳定，在λ取值过低或者过高时，精度值出现了大幅度的下降，这是容易理解的，因为λ代表了混入旧消息的比例，对于某些网络，旧消息的比例过大或者过小都会导致结果的失衡。如图3(b)和(c)所示，λ在所有取值范围内都使得两种评价指标下的精度表现出趋于稳定的结果，虽然有小幅度的波动，但是没有非常大的影响，所以本文可以选择一般的参数值。如设置λ=0.5，进行实验一。

3 结语

在众多社团发现技术中，置信传播算法是一类非常经典的概率图模型推理算法，具有很强的全局寻优能力，但该算法在迭代过程中会产生强烈的震荡，从而影响收敛速度和算法精度。通过大量研究，发现了导致震荡的3个主要原因，并且针对这3个原因提出了改进措施：为了达到收敛平滑，以权重的形式加入前一次迭代的消息，同时通过参数的调节，平衡新旧消息。此外，本文指出同步消息传递方式存在的问题，并创新性的提出异步消息传递方式，它能够修正同步方式存在的问题，增加收敛消息数量，对算法的速度和精度均能产生显著的影响。针对这两点改进本文在5个真实网络上进行了实验，实验结果表明两个改进都取得了显著效果。

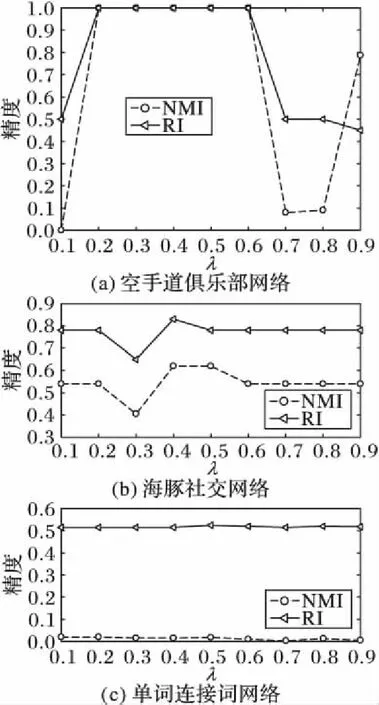
图3 参数λ对精度的影响Fig. 3 Effect of parameters λ on accuracy

为了能使改进后的算法具有更加广泛的应用范围，一些问题值得进行更深入的探讨，譬如：1)如何进一步提高算法速度，使得其能够在大规模网络上准确划分社团；2)现在的算法需要预先确定社团个数K，这是一个比较大的局限，如何自动并准确地确定K，是一个很有价值的挑战。

References)

[1] 杨博,刘大有,金弟.复杂网络聚类方法[J].软件学报, 2009, 20(1): 54-66.(YANG B, LIU D Y, JIN D. Clustering methods of complex networks[J]. Journal of Software, 2009, 20(1): 54-66.)

[2] 李慧嘉,严冠,刘志东,等.基于动态系统的网络社团线性探测算法[J].中国科学:数学, 2017, 47(2): 241-256.(LI H J, YAN G, LIU Z D, et al. Linear community detection algorithm based on dynamic network system[J]. Science China: Mathematics, 2017, 47(2): 241-256.)

[3] FORTUNATO S. Community detection in graphs[J]. Physics Reports, 2010, 486(3): 75-174.

[4] JIA S W, GAO L, GAO Y, et al. Defining and identifying cograph communities in complex networks[J]. New Journal of Physics, 2015, 17(1): 013044.

[5] YANG L, CAO X C, HE D X, et al. Modularity based community detection with deep learning[C]// Proceedings of the 25th International Joint Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2016:2252-2258.

[6] FANUEL M, ALAZ C M, SUYKENS J A. Magnetic eigenmaps for community detection in directed networks[J]. Physical Review E, 2016, 95(2):022302.

[7] ANDREI B, KHLOPOTINE A, SATHANUR V J. Optimized parallel label propagation based community detection on the Intel(R) Xeon Phi(TM) architecture[C]// Proceedings of the 27th International Symposium on Computer Architecture and High Performance Computing. Piscataway, NJ: IEEE, 2016: 9-16.

[8] WANG S F, GONG M G, SHEN B, et al. Deep community detection based on memetic algorithm[C]// Proceedings of the 2015 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2015: 648-655.

[9] 黄立威,李彩萍,张海粟,等.一种基于因子图模型的半监督社区发现方法[J].自动化学报, 2016, 42(10): 1520-1531.(HUANG L W, LI C P, ZHANG H S, et al. A semi-supervised community detection method based on factor graph model[J]. Acta Automatica Sinica, 2016, 42(10): 1520-1531.)

[10] ZHANG H Y, ZHAO T, IRWIN K, et al. Modeling the homophily effect between links and communities for overlapping community detection[EB/OL].[2016- 11- 20]. http://www.ijcai.org/Proceedings/16/Papers/554.pdf.

[11] JIN D, WANG H C, DANG J W, et al. Detect overlapping communities via modeling and ranking node popularities[C]// Proceedings of the 30th AAAI Conference on Artificial Intelligence. Menlo Park, CA: AAAI Press, 2016:172-178.

[12] NEWMAN M E J. Communities, modules and large-scale structure in networks[J]. Nature Physics, 2012, 8(1): 25-31.

[13] EWMAN M E J, SLY A. Stochastic block models and reconstruction[EB/OL].[2016- 11- 20]. http://www.stat.berkeley.edu/～jneeman/monesl12.pdf.

[14] DECELLE A, KRZAKALA F, MOORE C, et al. Asymptotic analysis of the stochastic block model for modular networks and its algorithmic applications[J]. Physical Review E: Statistical Nonlinear and Soft Matter Physics, 2011, 84(2): 066106.

[15] LANCICHINETTI A, RADICCHI F, RAMASCO J. Statistical significance of communities in networks[J]. Physical Review E: Statistical Nonlinear and Soft Matter Physics, 2010, 81(2):046110.

[16] ABBE E, BANDEIRA A S, HALL G. Exact recovery in the stochastic block model[J]. IEEE Transactions on Information Theory, 2015, 62(1):471-487.

[17] LAKEMEYER G, NEBEL B. Exploring Artificial Intelligence in the New Millennium[M]. San Francisco, CA: Morgan Kaufmann Publishers Inc, 2003: 239.

[18] STEINLEY D. Properties of the Hubert-Arable adjusted rand index[J]. Psychological Methods, 2004, 9(3): 386-396.

[19] DANON L, DIAZ G A, DUCH J, et al. Comparing community structure identification[EB/OL].[2016- 11- 20]. http://arxiv-web.arxiv.org/pdf/cond-mat/0505245.

This work is partially supported by the National Natural Science Foundation of China (61303110, 61502334), the Peiyang Scholar-Elite Scholar Program of Tianjin University (2017XRG- 0016).

YOUXinxin, born in 1993, M. S. candidate. Her research interests include community detection, data mining.

GEMeng, born in 1992, M. S. candidate. His research interests include deep learning, community detection.

Communitydetectionalgorithmbasedonbeliefpropagationincomplexnetworks

YOU Xinxin, GE Meng*

(SchoolofComputerSoftware,TianjinUniversity,Tianjin300350,China)

The classical Belief Propagation (BP) algorithm can inference the marginal probability distributions and maximum likelihood probability of all nodes by a finite number of iterations. However, BP algorithm always causes strong oscillation in the iterative process, and it uses synchronous way to pass messages which seriously affects the convergence rate. According to a lot of research, three main factors which caused oscillation were found: strong energy, close loop and contradictory direction. Furthermore, a new update formula and an asynchronous way of passing messages were proposed to solve above two problems. Stochastic block model was used to model the network generation process and the result of community division was obtained by using classical expectation maximization algorithm combined with BP. Extensive experimental results on real-world networks show the superior performance of the new method over the state-of-the-art approaches.

complex network; community detection; Belief Propagation (BP); stochastic block model; convergence rate

2017- 05- 16;

2017- 06- 07。

国家自然科学基金资助项目(61303110, 61502334)；天津大学北洋学者·青年骨干教师项目(2017XRG-0016)。

尤心心(1993—)，女，山东乐陵人，硕士研究生，主要研究方向：社团发现、数据挖掘； 葛檬(1992—)，男，浙江台州人，硕士研究生，主要研究方向：深度学习、社团发现。

1001- 9081(2017)11- 3115- 04

10.11772/j.issn.1001- 9081.2017.11.3115

(*通信作者电子邮箱gemengtju@163.com)

TP393

A