基于级联深度卷积神经网络的高性能图像超分辨率重构

郭 晓,谭文安,2

(1.南京航空航天大学 计算机科学与技术学院, 南京 211106； 2.上海第二工业大学 计算机与信息学院, 上海 201209)

基于级联深度卷积神经网络的高性能图像超分辨率重构

郭 晓1,谭文安1,2*

(1.南京航空航天大学 计算机科学与技术学院, 南京 211106； 2.上海第二工业大学 计算机与信息学院, 上海 201209)

为了进一步提高现有图像超分辨率重构方法所得图像的分辨率，提出一种高性能的深度卷积神经网络(HDCN)模型用于重构放大倍数固定的超分辨率图像。通过建立级联HDCN模型解决传统模型重构图像时放大倍数无法按需选择的问题，并在级联过程中引入深度边缘滤波器以减少级联误差，突出边缘信息，从而得到高性能的级联深度卷积神经网络(HCDCN)模型。基于Set5、Set14数据集进行超分辨率图像重构实验，证明了引入深度边缘滤波器的有效性，对比HCDCN方法与其他图像超分辨率重构方法的性能评估结果，展现了HCDCN方法的优越性能。

超分辨率; 图像重建; 深度卷积神经网络; 级联; 深度边缘滤波器

0 引言

受限于硬件设备，日常人们获取的数字图像分辨率普遍较低，无法满足实际需要。为了解决这一问题，可以采用单幅图像超分辨率重构(Single Image Super-Resolution，SISR)技术，由一幅低分辨率(Low-Resolution，LR)图像重构出一幅高分辨率(High-Resolution，HR)图像以获取更多的细节信息。该技术已广泛应用于计算机视觉与图形学、医学成像、安全监控等领域。

较为早期的单幅图像超分辨率重构技术大多基于插值，如双三次插值法(bicubic interpolation)[1]。插值方法得到的重构图像易出现模糊、振铃、锯齿等现象[2]。随后出现如迭代反向投影法(Iterative Back Projection，IBP)[3]等基于重构的方法，通过对图像降质过程建立观测模型，利用数学理论进行反向求解以重构高分辨率图像。基于重构的方法减少了锯齿、振铃等现象，但存在正则约束项的选择问题及配准问题等。近年来，基于学习的方法,如邻域嵌入法(Neighbor embedding)[4]、稀疏编码(Sparse coding)[5]构建包含LR图像和HR图像的样本库，通过训练得到样本库中LR/HR图像块之间的映射关系，从而指导图像超分辨率重建。文献[6]提出超分辨率卷积神经网络(Super-Resolution Convolutional Neural Network，SRCNN)通过深度卷积神经网络学习低分辨率图像到高分辨率图像实现端到端的映射，使单幅图像超分辨率重构技术得到质的飞跃。但目前该项技术依然存在以下问题：1)大部分模型重构超分辨率图像时放大倍数无法按需调整，需要重新训练模型来改变放大倍数。如文献[7]采用重新微调模型的方式改变图像放大倍数；文献[8]利用单个多层深度卷积神经网络同时学习不同的放大倍数，取得了优异效果。2)大部分基于卷积神经网络的重构模型训练时收敛慢，需要迭代运算次数甚至达到千万；网络层次较浅，无法学习表征更为复杂的图像信息。

本文研究主要贡献如下：1)为进一步提高现有方法重构超分辨率图像的分辨率，本文提出一种高性能的深度卷积神经网络(High-performance Deep Convolutional neural Network, HDCN)模型用以实现固定放大倍数的图像超分辨率重建；2)为解决重构图像时放大倍数无法按需调整的问题，提出高性能的级联深度卷积神经网络(High-performance Cascade Deep Convolutional neural Network, HCDCN)模型同时重构多个放大倍数的高分辨率图像，在级联过程中引入深度边缘滤波器，提升重构性能。与文献[6-9]等方法的实验对比证明了本文所提方法的优异性能。

1 相关工作

1.1 基于深度卷积神经网络的图像超分辨率重构

在SRCNN模型中，卷积神经网络只有3层，分别起到特征提取，非线性映射以及重构的作用。同样采取3层卷积神经网络的还有文献[9]中提出的高效子像素卷积神经网络(Efficient Sub-Pixel Convolutional neural Network，ESPCN)，该方法将起重构作用的反卷积层表示成卷积层的形式，在网络的最后一层提升图像大小。文献[7]对SRCNN模型进行改进，增加用于收缩和扩展模型参数的卷积层，使得模型可以在配置较低的电脑上得以训练，同时将起非线性映射作用的卷积层由1层扩展至4层，取得更优异的性能。文献[8]调整梯度下降时的迭代步长加速收敛，极大缩减了训练时间，采用20层卷积神经网络进行残差学习(residual-learning)，获得较好的高分辨率图像性能。文献[7-8]的实验结果表明：在一定条件下，增加卷积神经网络层数可以提升图像超分辨率重构的性能。

1.2 边缘滤波器

边缘滤波器广泛应用于计算机视觉和图像处理，既平滑了图像，又尽可能地保留了图像的边缘信息。早在20世纪90年代，文献[10]便提出了对滤波方向进行控制的边缘滤波器(Steerable Filter)，文献[11]提出了经典的双边滤波器(Bilateral Filter)，之后有很多方法都是基于双边滤波器，如文献[12-13]。文献[14]通过深度卷积神经网络建立了多种边缘滤波器的统一框架，融合各边缘滤波器原有特性，在降低计算复杂度的同时依然可以提升性能。

2 本文提出的模型

2.1 HDCN模型

受启发于文献[8]中“The deeper, the better”的思想，实验训练一个共d层的深度卷积神经网络用于实现放大倍数为s的图像超分辨率重构。网络结构见图1。

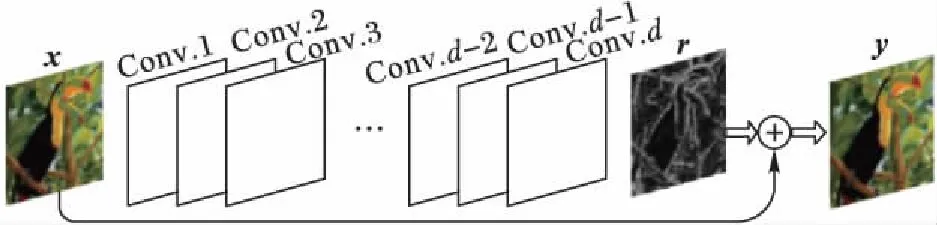
图1 HDCN模型结构Fig. 1 HDCN model architecture

图1中，模型输入是待重构图像通过双三次插值法放大s倍的结果图像x，输出是高分辨率图像y与输入图像x之间的残差r，将输入与输出相加即可得出放大倍数为s的高分辨率图像y。

除去网络结构中第一层从图像x中提取特征以及最后一层用于重构图像，其余卷积层都用于学习模型F，使得由模型F预测的残差值F(x)与真实残差r之间的误差最小。优化目标可表示如下：

(1)

传统深度网络随着深度的增加，梯度弥散致使训练难度不断加大，而深度残差网络在一定深度内(文献[15]中34层)可以尽可能地减小梯度弥散的影响，因此HDCN模型选择的学习目标是高分辨率图像y与输入图像x之间的残差r，而不是如传统神经网络将高分辨率图像y作为学习目标。

[15]中的34层深度残差网络设计规则：1)大部分使用3×3的卷积核；2)对输出映射特征大小相同的卷积层，设定相同数目的卷积核。因此在参数选择上，用于学习模型F的卷积层拥有相同的结构，每一层都具有64个大小为3×3×64的滤波器，最后一层只需要一个3×3×64的滤波器。考虑到深度残差网络大幅降低了训练更深层次神经网络的难度。因此在训练中可以采取较为激进的迭代策略，减少训练时间，详细的步长迭代策略见3.3节。

2.2 HCDCN模型

借助上述的HDCN模型，可以由一幅低分辨率图像重构出大小为原来s倍的高分辨率图片。为了同时得到其他重构倍数的高分辨率图片，可以将HDCN模型级联起来得到如图2所示的模型结构。例如，要想得到重构倍数为s2的高分辨率图片，仅需将低分辨率图片通过2次HDCN模型，每通过一次HDCN模型都会得到输入图像s倍的高分辨率图像。

图2 级联的HDCN模型结构Fig. 2 Cascaded HDCN model architecture

这种级联方式十分简单，但使用较少,如文献[16-17]。因为通过同一模型重复放大，存在放大误差的风险。为了减少这种风险，在层级之间引入深度边缘滤波器，在平滑图像的同时会保留图像的边缘信息。平滑图像可以减少因局部像素点偏差对后续重构造成的影响，同时边缘信息的保留有利于减少图像重构过程中的结构误差。深度边缘滤波器通过深度卷积神经网络建立了多种边缘滤波器的统一框架，极大减少了挑选合适边缘滤波器的工作量。最终得到的HCDCN模型如图3所示。

图3 HCDCN模型结构Fig. 3 HCDCN model architecture

(2)

图像超分辨率重构技术实质上是由低分辨率图像推理出丟失的高频分量以重构高分辨率图像，引入深度边缘滤波器会减少图像的细节信息，只要控制边缘滤波器的系数δ，在一定条件下，对性能仍有提升效果。详细的系数设置见3.3节。

3 实验

3.1 实验数据集

实验采用文献[18]中的91张图片作为训练集，经数据增强后为1 638张图片。测试集为国际通用的“Set5”[19]以及“Set14”[20]，总计19张图片。

3.2 评估路线

实验采用两种国际通用的评判标准衡量实验性能：峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)以及结构相似性(Structural SIMilarity，SSIM)。

峰值信噪比是使用最普遍和最为广泛的一种图像客观评价指标，它通过计算对应像素点间的误差，衡量图像质量。计算公式如下：

(3)

其中：H、W分别为图像的高度和宽度；m为每像素的比特数，一般取8；X(i,j),Y(i,j)分别表示图像X,Y中坐标点(i,j)的亮度值。PSNR的单位是dB，数值越大表示失真越小。

结构相似性SSIM分别从亮度、对比度、结构三方面度量图像相似性，其计算公式如下：

SSIM(X,Y)=l(X,Y)·c(X,Y)·s(X,Y)；

(4)

其中：μX、μY分别表示图像X和Y的均值，σX、σY分别表示图像X和Y的方差，σXY表示图像X和Y的协方差。C1、C2、C3为常数，为了避免分母为0的情况，通常取C1=(K1×L)2，C2=(K2×L)2，C3=C2/2，一般地K1=0.01，K2=0.03，L=255。

3.3 实验参数与实施

鉴于目前主流研究中重构倍数主要为2、3、4倍，因此s取2，同时，d取25，即HDCN模型是用于重构2倍高分辨率图片、拥有25层网络结构的深度卷积神经网络。

训练集的图片首先经过间隔为14的下采样，得到大小为51×51的子图像。训练过程中，每一批的图像数为64，冲量单元(momentum)为0.9，权重衰减(weight decay)为0. 000 1。在迭代步长选取策略上，传统深度卷积神经网络模型采取固定为0.000 1的步长,如文献[6-7,9]。实验采取较为激进

(5)

其中：iter为当前迭代次数，base_lr、gamma均取0.1,stepsize为116 840。最终迭代次数为467 360。实验中使用的GPU为GTX970，模型训练时间约30 h。

在HCDNC模型中，系数δ的选取不能过大，否则会减少图片的细节信息。实验中，固定模型中的其他参数，仅改变系数δ，比较不同系数δ下测试数据集的PSNR值。图4展示了在重构倍数为3时，系数δ与Set5测试集PSNR值的关系。滤波器选取为“shock filter”，beta取167.7。实验表明，在模型中其他参数固定时，当系数δ为0.011时，HCDNC模型的重构性能最佳。因此，系数δ定义如下：

(6)

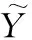
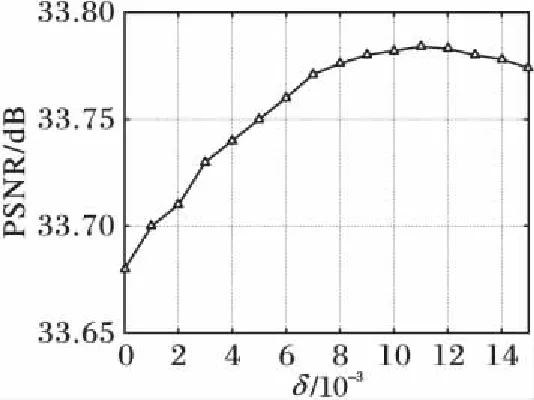
图4 重构倍数为3时，系数δ与Set5测试集PSNR值关系Fig. 4 Relationship between parameter δ and PSNR of Set 5 with scale factor×3

实验只训练了重构倍数为2的HDNC模型，因此重构倍数为4的高分辨率图片可以通过级联2个HDNC模型得到。而重构倍数为3的高分辨率图片可以选择通过改变重构倍数为4的高分辨率图片大小得到。

3.4 与其他方法对比

对比所提出的HCDCN方法在Set5以及Set14数据集上的实验结果与一些著名的图像超分辨率重构方法，如A+[22]、RFL[23]、SelfEx[24]以及SRCNN[5]，各实验条件下的平均PSNR值及SSIM值如表1所示，表中加粗标出的是当前实验条件下的最优结果。图5、图6中展示了部分实验结果，图中的评价指标分别为PSNR(单位dB)和SSIM，格式为(PSNR/SSIM)。

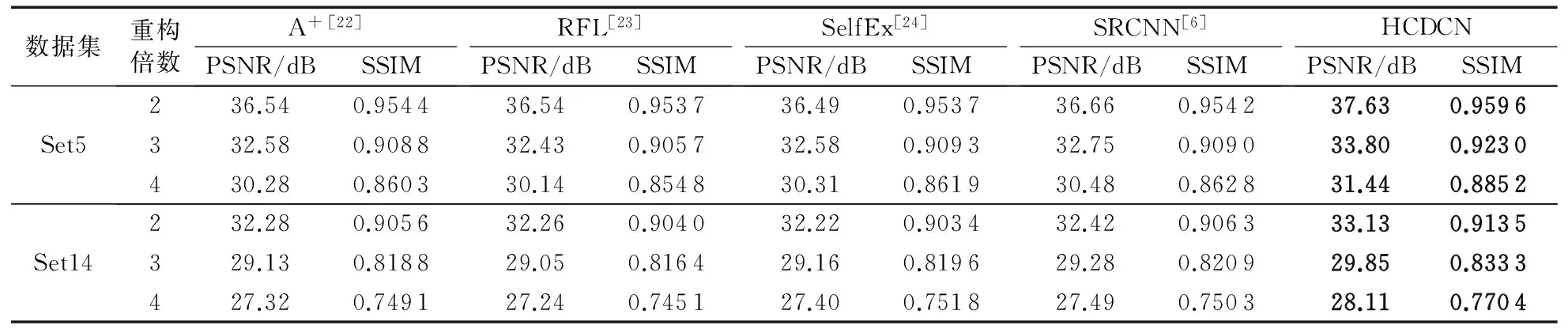
表1 重构倍数分别为2,3,4时，测试集Set5,Set14的平均PSNR值及SSIM值Tab. 1 Average PSNR/SSIM for scale factor ×2,×3 and ×4 on datasets Set5, Set14

图5 重构倍数为3时，Set5测试集中图像“butterfly_GT”的重构结果Fig. 5 Super-resolution results of “butterfly_GT” (Set5) with scale factor×3

图6 重构倍数为3时，Set14测试集中图像“ppt3”的重构结果Fig. 6 Super-resolution results of “ppt3” (Set14) with scale factor×3

对比发现，HCDCN模型的性能不逊色于近期的国际论文作结果，如ESPCN[9]、TNRD[25]、FSRCNN[7]、VDSR[8]，如表2所示，表中加粗标出的是当前实验条件下的最优结果。由于ESPCN模型只训练了重构倍数为3的模型，所以重构倍数2,4的实验结果缺失。缺失的数据用“—”表示。另外，前三种方法并未提供SSIM的数据，因此在表2中只比较了PSNR值。

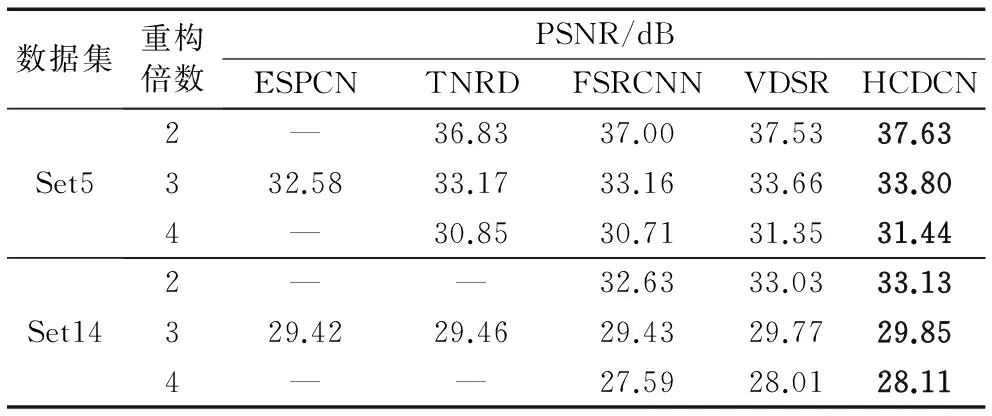
表2 重构倍数分别为2,3,4时，测试集Set5,Set14的平均PSNR值Tab. 2 Average PSNR for scale factor×2,×3 and ×4 on datasets Set5, Set14

4 结语

本文通过级联高性能深度卷积神经网络实现多放大倍数的单幅图像高分辨率重建。在级联过程中通过深度滤波器突出边缘信息优化重建结果，实验证明了级联方法及引入深度滤波器的有效性。下一步的工作尝试结合其他方法建立模型，如引入拉普拉斯金字塔模型对级联方法进行改进；改进模型的损失函数以解决重构图像部分模糊的问题。

此次采访短暂而丰富，记者们不仅了解了忠旺集团的整个发展历程，参观了生产车间，感叹于忠旺集团的雄厚实力，而且也看到了新技术对于产品生产所产生的革命式改变，我们相信搅拌摩擦焊未来不仅在铝合金加工行业，在其他行业也同样能够发挥专长，为产品生产提供更为广阔的技术平台。

参考文献(References)

[1] KEYS R. Cubic convolution interpolation for digital image processing [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1981, 29(6):1153-1160.

[2] 曾坤. 基于学习的单幅图像超分辨率重建的若干关键问题研究[D]. 厦门: 厦门大学, 2015.(ZENG K. Research on some key problems of single image super-resolution reconstruction based on learning [D]. Xiamen: Xiamen University, 2015.)

[3] IRANI M, PELEG S. Improving resolution by image registration [J]. Graphical Models and Image Processing, 1991, 53(3): 231-239.

[4] 曾俊国. 基于稀疏邻域嵌入法的图像超分辨技术研究[J]. 科学技术与工程, 2013, 13(7):1840-1846.(ZENG J G. Image super resolution based on sparse neighbor embedding[J]. Science Technology and Engineering, 2013, 13(7): 1840-1846.)

[5] 沈松, 朱飞, 姚琦,等. 基于稀疏表示的超分辨率图像重建[J]. 电子测量技术, 2011, 34(6):37-39.(SHEN S, ZHU F, YAO Q, et al. Based on sparse representation for super-resolution image reconstruction[J]. Electronic Measurement Technology, 2011, 34(6): 37-39.)

[6] DONG C, CHEN C L, HE K, et al. Learning a Deep Convolutional Network for Image Super-Resolution [M]. Berlin: Springer International Publishing, 2014:184-199.

[7] DONG C, CHEN C L, TANG X. Accelerating the super-resolution convolutional neural network[C]// Proceedings of the 14th European Conference on Computer Vision. Berlin: Springer, 2016:391-407.

[8] KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2016:1646-1654.

[9] SHI W, CABALLERO J, HUSZR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Washington, DC: IEEE Computer Society, 2016: 1874-1883.

[10] FREEMAN W T, ADELSON E H. The design and use of steerable filters[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1991, 13(9): 891-906.

[11] TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]// Proceedings of the Sixth International Conference on Computer Vision. Piscataway, NJ: IEEE, 1998: 839.

[12] YANG Q, TAN K H, AHUJA N. Real-time O(1) bilateral filtering[C]// Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2009:557-564.

[13] YANG Q, WANG S, AHUJA N. SVM for edge-preserving filtering[C]// Proceedings of the 2010 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2010:1775-1782.

[14] XU L, REN J S, YAN Q, et al. Deep edge-aware filters[EB/OL].[2016- 10- 20]. http://www.jimmyren.com/papers/Poster_ICML-2015.pdf.

[15] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2016:770-778.

[16] CUI Z, CHANG H, SHAN S, et al. Deep network cascade for image super-resolution[C]// Proceedings of the 13th European Conference on Computer Vision. Berlin: Springer, 2014:49-64.

[17] WANG Z, LIU D, YANG J, et al. Deep networks for image super-resolution with sparse prior[C]// Proceedings of the 2015 IEEE International Conference on Computer Vision. Washington, DC: IEEE Computer Society, 2015:370-378.

[18] YANG J, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861.

[19] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding[EB/OL]. [2016- 10- 20].http://www.irisa.fr/prive/Aline.Roumy/publi/12bmvc_Bevilacqua_lowComplexitySR.pdf.

[20] ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse-representations[C]// Proceedings of the 7th International Conference on Curves and Surfaces. Berlin: Springer-Verlag, 2010:711-730.

[21] JIA Y, SHELHAMER E, DONAHUE J, et al. Caffe: convolutional architecture for fast feature embedding[C]// Proceedings of the 22nd ACM International Conference on Multimedia. New York: ACM, 2014:675-678.

[22] TIMOFTE R, SMET V D, GOOL L V. A+: adjusted anchored neighborhood regression for fast super-resolution[C]// Proceedings of the 12th Asian Conference on Computer Vision. Berlin: Springer, 2015:111-126.

[23] SCHULTER S, LEISTNER C, BISCHOF H. Fast and accurate image upscaling with super-resolution forests[C]// Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015:3791-3799.

[24] HUANG J B, SINGH A, AHUJA N. Single image super-resolution from transformed self-exemplars[C]// Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015:5197-5206.

[25] CHEN Y, POCK T. Trainable nonlinear reaction diffusion: a flexible framework for fast and effective image restoration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015, 39(6): 1256-1272.

This work is partially supported by the National Natural Science Foundation of China (61672022).

GUOXiao, born in 1994, M. S. candidate. His research interests include machine learning, deep learning, image restruction.

TANWenan, born in 1965, Ph. D., professor. His research interests include software service engineering, trusted service computing and composition, collaborative computing, business process intelligence.

High-performanceimagesuper-resolutionrestructionbasedoncascadedeepconvolutionalnetwork

GUO Xiao1, TAN Wenan1,2*

(1.CollegeofComputerScienceandTechnology,NanjingUniversityofAeronauticsandAstronautics,NanjingJiangsu211106,China;2.CollegeofComputerandInformation,ShanghaiPolytechnicUniversity,Shanghai201209,China)

In order to further improve the resolution of existing image super-resolution methods, a High-performance Deep Convolution neural Network (HDCN) was proposed to reconstruct a fixed-scale super-resolution image. By cascading several HDCN models, the problem that many traditional models could not upscale images in alternative scale factors was solved, and a deep edge filter in the cascade process was introduced to reduce cascading errors, and highlight edge information, High-performance Cascade Deep Convolutional neural Network (HCDCN) was got. The super-resolution image reconstruction experiment was carried out on high-performance cascade deep convolution neural network (HCDCN) model on Set5 and Set14 datasets. The experimental results prove the effectiveness of introducing the deep edge-aware filter. By comparing the performance evaluation results of HCDCN method and other image super-resolution reconstruction method, the superior performance of HCDCN method is demonstrated.

super-resolution; image reconstruction; deep convolutional neural network; cascade; deep edge-aware filter

2017- 05- 16;

2017- 06- 05。

国家自然科学基金资助项目(61672022)。

郭晓(1994—)，男，江苏南京人，硕士研究生，主要研究方向：机器学习、深度学习、图像重建； 谭文安(1965—),男,湖北荆州人，教授, 博士, 主要研究方向：软件服务工程、可信服务计算与组合、协同计算、业务过程智能。

1001- 9081(2017)11- 3124- 04

10.11772/j.issn.1001- 9081.2017.11.3124

(*通信作者电子邮箱wtan@foxmail.com)

TP391.41

A