提炼基本模型 提高解题能力

马晓琴

[摘  要] 在几何学习中，我们要善于归纳、提炼并储备基本图形，并让学生慧眼识图，当不完全的“形”呈现于眼前，自然想到去构造基本图形，从而找到解决问题的突破口，出奇制胜.

[关键词] 基本模型;解题能力

几何与图形领域中存在着许多基本图形，在具体的情境中加强对基本图形的研究，并让学生慧眼识图，从复杂图形中找出基本图形，强化模型意识，往往可以找到解决问题的突破口，出奇制胜. 笔者结合平时教学梳理了几种常见的基本图形与大家一起分享.

基本图形一：“角平分线+垂直”证全等

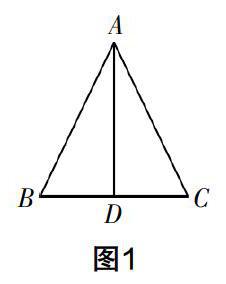
已知，如图1，在△ABC中，AD平分∠BAC，AD⊥BC，求证：△ABD≌△ACD.

分析  根据“ASA”即可证得.

例1？摇 如图2，Rt△ABC中，AB=AC，∠1=∠2，CE⊥BD，且交BD的延长线于E. 试猜想BD与2CE的关系，并说明理由.

分析  此题中既有角平分线，又有垂直，联想基本图形，如图3，想到延长BA，CE相交于点F，利用基本图形，可证△FBE≌△CBE，得CE=EF，即CF=2CE，欲找BD与2CE的关系，只要找BD与CF的关系，于是只要证明△ABD≌△ACF即可.

基本图形二：“垂直+垂直”证两个角相等

已知，如图4，∠BAC=90°，AD⊥BC，求证：∠BAD=∠C，∠CAD=∠B.

分析  由∠BAC=90°，得∠BAD+∠DAC=90°，由AD⊥BC，得∠C+∠DAC=90°，两式结合，得∠BAD=∠C，同理可得∠CAD=∠B.

例2？摇 已知，在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点.

（1）如图5，直线BF⊥CE于點F，交CD于点G，求证：AE=CG;

（2）如图6，直线AH⊥CE于点H，交CD的延长线于点M，找出图中与BE相等的线段，并证明.

分析 （1）由∠ACB=90°，BF⊥CE，想到利用基本图形，证得∠ACE=∠CBG，欲证AE=CG，只要证△ACE≌△CBG即可.

（2）由∠ACB=90°，AH⊥CE，想到利用基本图形，证得∠MAC=∠ECB，再证△MAC≌△ECB即可找到与BE相等的线段.

基本图形三：“平行+中点”证全等

已知，如图7，AB∥CD，E是AD的中点，求证：△ABE≌△DCE.

分析  由AB∥CD，得∠A=∠D， ∠B=∠C，由E是AD的中点，得AE=DE，即可证得△ABE≌△DCE.

分析  由AB⊥BC，AB⊥AD，可证得AD∥BC，由点E是CD的中点，联想基本图形，想到延长AE交BC于点F，即可证△ADE≌△CFE，得CF=AD=5，由BC=10，得BF=5，由AB⊥BC，AB=12，得AF=13，由△ADE≌△CFE，得AE=1/2AF=13/2.

基本图形四：“等边三角形+等边三角形”证全等

已知：如图10，△ABC和△CDE都是等边三角形，求证：△ACD≌△BCE.

分析  由△ABC和△CDE都是等边三角形，得AC=BC，DC=EC，∠ACB=∠DCE. 等式两边同时加上∠BCD，得∠ACD=∠BCE，即可证得△ACD≌△BCE.

例4  如图11，△ABC和△EFC都是等边三角形，AD是△ABC的高，AB=4，若点E在直线AD上运动，连接DF，则在点E运动过程中，求线段DF的最小值.

分析  由△ABC和△EFC都是等边三角形，联想基本图形，想到证全等，但是这样的三角形不存在，于是想到连接BF，构造△BFC≌△AEC. 由△ABC是等边三角形，AD是△ABC的高，得D是BC的中点，想到取AC的中点D′，连接D′E，如图12，于是DF的长相当于△AEC中对应位置D′E的长，要使DF最小，只要使D′E最小即可，因为D′是定点，E是动点，显然当D′E⊥AD时最小，即可求出最小值.

基本图形五：“平行+角平分线”证等腰三角形

已知，如图13，AB∥CD，CB平分∠ACD，求证：AC=AB.

分析  由AB∥CD，得∠B=∠BCD，由CB平分∠ACD，得∠ACB=∠BCD，于是∠B=∠ACB，证得AC=AB.

例5 如图14，若BD，CD分别平分△ABC的一个内角和一个外角，DE∥BC分别与AB，AC交于点E，F，DE=8，EF=3.5，求BE+CF的值.

分析  由DE∥BC，BD平分△ABC的一个内角，联想基本图形，想到证BE=DE;由DE∥BC， CD平分△ABC的一个外角，联想基本图形，想到证CF=DF，由DE=8，得到BE=8，由EF=3.5，得DF=4.5，于是CF=4.5，所以BE+CF=12.5.

波利亚曾说过：“解题的成功，要靠正确的转化. ”在几何学习中，我们要善于归纳、提炼并储备基本图形. 心理学研究表明：当不完全的“形”呈现于眼前时，视觉中有一种强烈的追求完整、和谐、简洁的倾向，在解题中自然会想到去构造基本图形，那么解题思路就会豁然开朗，可以大大提高解题的速度和正确率，从而提高解题能力.