变式在初中数学教学中的应用思考

许祥

[摘  要] 运用逆向思维与横向思维对典型例题进行条件、结论、图形的改变并将其变成变式题组，是教师课堂教学中的有效措施，学生在这种变式训练的长期积累中一定能形成更加完整而有意义的知识结构，并对数学学习充满新鲜感与动力.

[关键词] 生成;拓展延伸;思想交融;条件;结论;变式

学生彻底理解概念并在解题与思维能力方面获得长足的发展都离不开有效的变式教学. 历年来的中考试题虽然有很多题目都是源自于教材而设计的，但大多又都是高于教材的. 因此，教师在实际教学中应着眼于教材及教材中的典型例题与习题并探寻知识的“生长点”，将题中所蕴含的思想方法一一挖掘出来并揭示出问题的本质，使学生能够真正把握问题本质并最终学会该类题目的解决方法.

着眼于解题方法的生成之处进行变式

很多题目的解法都不是唯一的，因此，教师在实际教学中应引导学生探索解题的不同方法并进行方法的比较以促进学生发散思维的发展.

案例1  如果代数式y²+3y的值是5，那么，代数式4y²+12y-20的值为______.

解法1：解方程y²+3y=5，代入求值，但较烦琐.

解法2：由y²+3y=5，所求代数式的前两项结合并提出一个4，整体代入.

学生在解法的探寻与比较中很快尝到解法2的甜头并解出：当x=1时，代数式ax²+bx+1的值为3，则（a+b-1）（1-a-b）的值为-1. 学生从不同的角度对此题进行了不同方法的思考与体验.

着眼于拓展延伸之处进行变式

学生对事物实质与发展趋势的了解以及对所学知识的深化都能在拓展延伸训练与练习中一一实现，因此，教师在实际教学中应善于挖掘教材例题、习题的内涵与实质并获得源于教材、却又高于教材的题目，使学生能够在这些更具探索价值的好题中进一步理顺知识间的联系. 因此，教师应着眼于学生学习中的实际需求并结合学生已有水平、能力与经验进行各种形式与内容的拓展设计，使学生能够在各种拓展训练中不断深化自己对知识的理解.

案例2  在△ABC中，AD⊥BC于D，AE平分∠BAC，若∠B=30°，∠C=70°，则∠DAE=______.

变式1：若∠C-∠B=30°，则∠DAE=______. 引导学生在变式练习中掌握整体考虑问题这一重要思想.

变式2：∠C-∠B=α（∠C>∠B），请用含α的代数式表示∠DAE的度数.

学生在变式中很快掌握了用字母表达式表示一般规律的方法，由此可见，看似平淡实则精彩的变式往往能够促进学生对知识纵横联系的掌握与理解. 因此，教师在教学之余应善于对例题进行再挖掘与变式设计，要舍得在变式研究上花时间，教师设计的例题越是精炼，学生在学习中获得的感悟就越多，着眼于小题的变式设计与教学往往能够使学生获得能力的大提升.

着眼于思想交融之处进行变式

着眼于数学思想渗透与融合的变式还能促进学生对知识、方法的本质规律形成更加深刻的理性认识，并因此实现数学素质与数学思维的高度发展.

案例3  已知线段AB=8 cm，点C在直线AB上，M，N分别是AC，BC的中点，线段MN的长是______.

运用分类讨论的思想对C在A，B点左边、之间、右边这三种情况进行求解，分类讨论能够有效防止学生片面思考问题，完整解题的过程也对学生思维的严谨性进行了很好的锻炼.

变式1：已知线段AB=10 cm，点C为AB上任意一点，M，N分别为AC，CB的中点，MN的长度为______.

变式2：在直线l上顺次取A，B，C三点并使AB=5 cm，BC=3 cm，假如线段AC的中点是O，则线段OB的长度为______.

学生在变式训练中对概念之间的区别与联系都能建立更加清晰而准确的认知，充分认识到各知识点之间的运动、变化与联系的同时也更加善于发现特殊条件与关键条件.

着眼于条件进行变式

对习题中的条件进行增加、减少或者变更都是条件变式的形式.

案例4  如图1，已知∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF，（1）若以“SAS”为依据，还需添加______这一条件;（2）若以“ASA”为依据，还需添加______这一条件;（3）若以“AAS”为依据，还需添加______这一条件.

学生在此题的有效练习中完全掌握了两个三角形全等的判断方法.

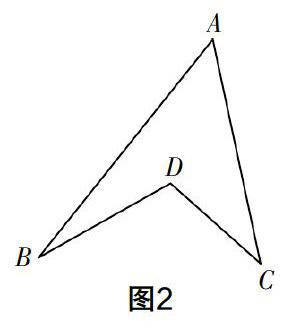
案例5  如图2，该图形中隐藏的数学知识有哪些？请结合图形解决以下问题：观察“规形图”的同时对∠BDC和∠A，∠B，∠C之间的关系进行探究，并说明理由.

此基础题的解决需要运用三角形的外角知识，因此，学生在解決此题时应根据解题需要添加辅助线并以此构造三角形的外角，得到∠BDC=∠A+∠B+∠C.

变式：请直接利用上述结论解决下列问题：

（1）如图3所示，将三角尺XYZ置于△ABC之上，使直角边XY，XZ刚好经过B，C两点. 若∠A=50°，则∠ABX+∠ACX=_____.

（2）如图4，DC平分∠ADB，EC平分∠AEB. 若∠DAE=50°，∠DBE=130°，求∠DCE的度数.

（3）如图5，∠ABD、∠ACD的10等分线相交于点G₁，G₂，…，G₉. 若∠BDC=140°，∠BG₁C=77°，求∠A的度数.

角平分线的条数从一条增至两条直至很多条的变式将题目的难度也逐步提高，学生在环环相扣的知识中对∠BDC，∠BG₁C与∠A的关系进行了探究，由特殊到一般的探索与发现对学生解题创新能力的锻炼是极有价值的.

着眼于结论进行变式

案例6  如图6，△ABC与△ADC是两个等边三角形，点E从点B出发沿BA方向运动至点A停止，同时点F以相同的速度从点A出发沿AD方向运动到点D停止，连接EC，FC. 在点E，F运动过程中∠ECF的大小会随之变化吗？请说明理由.

变式1：在点E，F运动过程中，以点A，E，C，F为顶点的四边形的面积会产生变化吗？请说明理由.

变式2：若点E，F在射线BA，AD上继续运动下去，原题中的结论是否还成立呢？

着眼于结论进行的变式在深化习题的同时也能帮助学生更好地挖掘知识内容的深度.

着眼于图形进行变式

图形的变化是几何变式题目中经常会用到的方式，解决几何变式题的关键在于寻找图形的不变性以及在复杂图形中分解出基本图形.

案例7  五角星及其变形.

如图7①，五角星形狀中∠A+∠B+∠C+∠D+∠E=______;学生联系三角形的内角和定理与外角和定理将5个角看成在一个三角形中，很快得出这5个角的和为180°.

如图7②，将图7①中的A点下移至BE上，此时∠CAD+∠B+∠C+∠D+∠E的和会产生变化吗？请说明理由. 学生在一定的思考与讨论后得出答案仍是180°.

如图7③，将图7②中的点C上移至BD上，此时∠CAD+∠B+∠ACE+∠D+∠E的和会产生变化吗？请说明理由. 教师引导学生在观测图形的基础上对知识的灵活应用进行进一步的体会与更多变式.

如图7④，CD，BE分别为AB，AC边上的中线，延长CD到F，使FD=CD，延长BE到G，使EG=BE，则AF和AG相等吗？F，A，G这三点在一条直线上吗？请说明理由.

运用逆向思维与横向思维对典型例题进行条件或结论的改编，呈现一组变式题，或者对其进行图形的改编，形成变式题组，是教师课堂教学中将所学知识点进行覆盖与整合的有效措施. 很多学过的零散知识点因为教师精心的变式设计而被整合到了一起，分散的知识点被精心设计成了一条有意义的思路. 学生在这种知识点全面覆盖的变式训练中长期积累，一定能够形成更加完整而有意义的知识结构，不断体会到新鲜、令人好奇的内容. 这些积极的学习情绪不仅让学生对所学知识与变式探究更加热情，还能使学生在解题思路不断开拓与发散的过程中产生更多的体验与感悟，发现问题的意识也会在不断的变式探究与经验积累中逐步形成，这对于学生产生并保持数学学习的新鲜感与动力是有着积极意义的.