探究变化 突破难点 总结方法

仓春燕

[摘  要] 教学“用方程解决行程问题”时，可以以线形示意图为切入点，带领学生在操作活动中经历不同情况、不同条件下探寻正确的线形示意图的过程，学会有条理地思考与表达.

[关键词] 探究;体验;突破;总结

基于价值判断的教学分析

“用方程解决行程问题”的教学价值往往被解读为找到等量关系列方程的技能，这固然是用方程解决行程问题的教学价值和学习要求，但它的价值不仅于此. 我们在找等量关系之前，还需解决如下问题：一，如何在整体层面上理解这个动态过程;二，如何通过媒介展示这个动态过程，以便快速地找出等量关系后列方程. 因此，“用方程解决行程问题”的教学价值还需继续挖掘.

学生是在经历了从问题到方程、解一元一次方程的基础上学习用一元一次方程解决实际问题的. 小学时学生已学习过用算术方法解决行程问题，所以教学时可让学生在温故的基础上深刻体会用方程解决问题的优势，并逐步建立起用方程刻画现实问题的数学模型，从而达到知新的目的. 在此过程中，我们不可避免地要借助媒介——“线形示意图”来寻找相等关系.

基于教学分析的教学过程

1. 复习回顾，探寻策略

与学生一起回顾行程问题涉及的路程、速度和时间的关系：路程=速度×时间.

（教师板书课题：用方程解决行程问题）

（1）利用旧知，解决问题

甲、乙两站相距360 km，一列快车由甲站开出，每小时行驶72 km;一列慢车由乙站开出，每小时行驶48 km. 若两车同时出发，相向而行，设两车行驶x h相遇，则可以列出方程：______.

（学生迅速根据“两车行驶的路程之和等于甲、乙两站之间的距离”列出方程： 72x+48x=360）

（2）引出新知，寻求方法

甲、乙两站相距360 km，一列快车由甲站开出，每小时行驶72 km;一列慢车由乙站开出，每小时行驶48 km. 若两车同时出发，同向而行（快车在后、慢车在前），设行驶x h后快车追上慢车，则可以列出方程：______.

（学生思考片刻，认为直接列方程不容易，于是笔者引导学生画出线形示意图）

2. 体验画图，探究变化

（1）初步感受线形示意图的画法并用它来找等量关系

笔者提示学生：假如有困难，可以画出线形示意图，并找到两题的相同之处和不同之处.

学生发现：第一题是两车相向而行，最后相遇;而第二题是快车追慢车，最后追上. 两题的相同点是两车的最终位置是同一个点，但画图时要注意各自的运动方向，以及两车出发点的位置. 经过分析，不少学生已经能够画出示意图（如图1和图2）.

学生可以迅速地从线形示意图上看出，第二题可根据等量关系“快车行驶的路程-慢车行驶的路程=两地的距离”列出方程：72x-48x=360.

（2）探究不同线形示意图所表示的不同情况

教师要引导学生发现：相遇问题，两车行驶的方向不同;而追及问题，两车行驶的方向相同.

（教师在黑板上板书：按方向不同分成两类）

生1：对于两车出发的时间，可以是同时出发，也可以是不同时出发;对于两车的出发地点，可以从同一地方出发，也可以从不同地方出发.

师：很显然，图1和图2都属于从同一时间、不同地点出发，可将生1所说的另外两种情形分别补充在对应的分类和各自的线形示意图下.

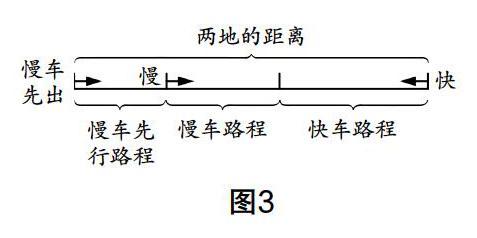
师：请同学们根据上述不同情况仔细观察线形示意图（图3和图4），说出它们是哪种情形，并分别找出各自的等量关系.

（学生先独立思考，然后小组讨论，教师巡视倾听，有目的地选择分析清楚、表述清晰的学生来回答）

生2：图3是方向相反的相遇问题，慢车先出发一段时间，快车才出发，属于不同时间不同地点出发的情况. 图4是追及问题，慢车本来就在快车前面，又先出发了一段时间，然后快车才出发去追慢车，图4也属于不同时间不同地点出发的情况.

（教师边听边板书，有目的地将各自的情形写在对应线形示意图下，同时引导学生找到等量关系）

生3：图3中，慢车先行驶的路程+慢车和快车一起行驶的路程之和=两地之间的距离;图4中，两地之间的距离+慢车先行驶的路程+慢车后面行驶的路程=快车行驶的路程.

师：请同学们根据黑板上的分类想一想，是否还有不同的情况是我們没有考虑到的.

生4：相遇问题和追及问题中还有同时同地点出发、不同时间同地点出发这两种情况.

（根据学生的回答，结合已有的线形示意图，板书完成所有分类，如表1）

师：请同学们尝试着画一画还没有画出线形示意图的情形.

（分成两组，左半组画相遇问题的另外两种情形，右半组画追及问题的另外两种情形）

设计意图 为了分类的完整性，学生发现同时同地点出发没有研究的意义，并发现还有环形行程线路可以研究，可在两组中各挑一位学生在黑板上画出这两种情形.

师：请同学们找出图5～图8四个图的等量关系.

生5：图5中，快车行驶的路程+慢车行驶的路程=环形一圈的长;图6中，快车行驶的路程-慢车行驶的路程=环形一圈的长;图7中，慢车先行驶的路程+慢车和快车一起行驶的路程之和=环形一圈的长;图8中，慢车先行驶的路程+慢车后行驶的路程=快车行驶的路程.

至此，行程问题中一些主要变化情况的线形示意图都画出来了，下面就需要运用线形示意图来解决实际问题了.

3. 突破难点，解决问题

例1 敌、我两军相距37 km，敌军以6 km/h的速度逃跑，我军同时以9 km/h的速度追击，并在即将追上敌军时与敌军发生了战斗. 已知发生战斗时我军距敌军1 km，问：战斗是在开始追击后几小时发生的？

设计意图 这是一个追及问题，但与上面的情形均不同——最后没追上，所以最终双方的位置不一样，不过这不影响同学们用已熟悉的线形示意图来展现这一变化. 此题主要考查了学生灵活应用知识的能力，避免学生停留在模仿层面.

例2 运动场跑道一周的长是400 m，小红跑步的速度是爷爷的5/3倍，他们从同一地点沿跑道的同一方向同时出发，5 min后小红第一次追上爷爷. 小红和爷爷跑步的速度各是多少？

变式 运动场跑道一周的长是400 m，小红跑步的速度是爷爷的5/3倍，他们从同一地点沿跑道的同一方向同时出发，5 min后小红第一次追上爷爷. 如果小红追上爷爷后立即转身沿相反方向跑，几分钟后小红又一次与爷爷相遇？

设计意图 对于环形路线问题，前面只探索了如何画出线形示意图，并没有用它来解决实际问题，之所以安排这样一个例题，目的是让学生在实际问题中感知并尝试用刚刚所画的线形示意图来解决. 变式能让学生再次充分体会画线形示意图找等量关系的优势，能完善原有的知识框架，也能充实本节课的研究内容.

4. 梳理小结，总结方法

师生共同回顾线形示意图在不同条件下的变化情况，以及根据找到的等量关系如何列方程. 教学中教师应引导学生突破如何画线形示意图这一难点，让学生感悟数形结合思想，鼓励他们探究数学中的相关变化.

基于教学过程的教学思考

行程问题一直是教学中的难点，之所以难，是因为这类问题题型多，综合变化多，要求学生对动态过程进行演绎和推理. 本节课在众多的题型和变化中，仅局限于两个物体的运动，先研究最基本的直线行程，当直线行程已无研究价值时，研究环形行程. 学生以把文字描述的行程过程还原成对应的数学图形为突破点，探究行驶方向、出发时间、出发地点三种情况的组合变化所对应的不同的线形示意图，教学时应强化如何画图，从而带领学生找出等量关系，最后列方程解决问题.

1. 在画图体验中深化对运动过程的分析与理解

本节课意在让学生初步掌握行程问题中的一些基本题型，课本上画线形示意图只是明确其是过程的辅助工具，并没有要求学生能画出不同情形的线形示意图. 本节课如此安排，似乎浪费了一些时间，但它是最有利于我们分析运动过程的工具，所以研究不同情形的示意图还是非常有必要的. 如果单纯地就一题而画一图，学生只能就题论题，换条件后可能就不会画图，从而难以找到等量关系列方程. 所以，本节课从简单的情形入手，与学生一起探索如何画图以及画图的关键点. 且教学中通过条件的变化组合，能让学生经历画出不同情形示意图的过程，在体验中深化对过程的理解.

2. 在不同情形的变化拓展中提升对问题的理解能力

本节课引导学生对不同情形进行分类后，笔者没有让学生画图，而是直接给出两种情形的示意图，让学生找出对应的情况. 之所以这样安排，是着眼于学生已有的能力，让学生在探究如何画复杂示意图的过程中有一个梯度，起到给学生示范如何画复杂情形示意图的作用. 随后让学生自己尝试着画剩下情形的示意图，学生便有图可依，会自己尝试着改变图形以体现条件的变化. 这样既能促进学生养成画图的习惯，也能内化数形结合的本质，提升学生的思维能力.

3. 在思维活动中通过总结达到思维内化、应用提升

本节课最终总结出的技巧并没有直白地告诉学生，而是让学生在活动过程中通过思维内化而得到，这更符合知识学习的本质. 现代意义的问题解决更注重解决问题的过程、策略，以及思维方法，更注重解决问题过程中情感、态度与价值观的培养，强调过程与结果并重. 只要我们长期坚持这样的数学知识学习过程，学生必能将学习过程中的思维过程、思维方法内化为将来走向社会解决问题的基本素养. 其实，数学作为一门基础学科，会在培养学生的基本能力中起着潜移默化的作用.

结语

“探究—突破—总结”不仅是画线路图解决行程问题的过程，还是所有探究式学习活动的过程，所以这样的教学过程及设计理念适合所有的探究活动设计与建构.

新一轮课程改革倡导自主、探索、合作的学习方式，倡导“以学生为主体”的理念，作为一线教师，急需逐步改变学生被动学习的现状，所以教师在改变教学方法的同时，更需要换位思考，即站在學生的角度思考问题，切实可行地从学生的难点入手，关注知识的本质，激发学生的兴趣，引导他们开启思维，探究问题的前因后果，达到融会贯通、主动学习、内化思维的目的.