基于改进有效序值的高维多目标算法
2018-01-06魏静萱
胥 宁,魏静萱,赵 龙
(西安电子科技大学 计算机学院,陕西 西安 710071)
基于改进有效序值的高维多目标算法
胥 宁,魏静萱,赵 龙
(西安电子科技大学 计算机学院,陕西 西安 710071)
针对有效序值排序高维多目标优化算法的不足,文中提出一种基于改进的有效序值的高维多目标优化算法。该算法提出多边形杂交算子,用以提高种群的多样性,同时,文中还提出基于ε-占优的有效序值排序方法,从而增加收敛压力,提高收敛速度。通过标准测试函数实验验证了所提算法的有效性。
高维多目标优化;有效序值; ε-占优
随着多目标优化问题在实际应用[1-2]中目标个数越来越多,高维多目标优化问题(目标个数大于或等于4个)已经成为进化领域的研究热点问题。但是随着目标个数的增加,高维多目标优化问题存在一些难点问题[3-4]。为解决这些难点问题,文献[5]提出新的占优机制来解决高维多目标优化问题。Zhang和Li等人[6-8]将传统的数学规划方法应用到多目标优化问题,用单目标优化算法来解决高维多目标优化问题。Deb等人[9-10]提出基于参考点的非支配排序算法法,通过参考点找出最优解。文献[11]提出的有效序排序算法(Preference Order Genetic Algorithm, POGA),采用一种新的排序方式来解决高维多目标问题。
虽然POGA算法能够很好的解决高维多目标优化问题,但仍存在不足,例如采用单点交叉,解的多样性受到了限制。为解决这些不足,本文首先提出一种新的交叉算子(多面体交叉算子),目的是为了提交解的多样性。然后提出一种基于ε-占优的有效序值的算法,为了提高解的收敛压力和收敛速度。最后提出一种新的计算拥挤度算法(超体积算法)。
1 高维多目标中的概念
1.1 高维多目标问题的相关定义
对于一个具有n个决策变量,m个目标变量,p+q个约束问题可表示为
(1)
其中,x=(x1,x2,…,xn)∈X⊂Rn为n维决策矢量;y=(y1,y2,…,yn)∈Y⊂Rm为m维的目标矢量。Y为目标空间,目标函数F(x)定义了决策空间向目标空间的映射函数。
对高维多目标算法中的非支配最优解集的定义如下:
定义1Pareto占优:假设xA,xB∈X当且仅当∀i∈{1,2,…,m};fi(xA)≤fi(xB)
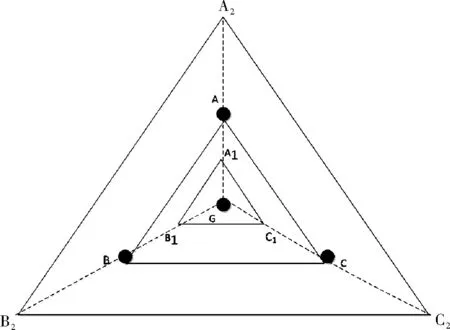
∧∃i∈{1,2,…,m}:fi(xA) (2) 定义2Pareto最优解:当且仅当∃x∈X:xx*时,这个解x*∈X被称为Pareto最优解。 定义3Pareto最优解集: p*{x*|∃x∈X:xx*} (3) 其中,p*表示最优解集;x*表示最优解。 定义4Pareto前沿面: PF={F(x*)=(f1(x*),…,fm(x*))|x*∈P*} (4) 其中,p*表示最优解集;PF表示最优解集构成的Pareto前沿面。 由于多目标优化问题的最优解是一个解集,因此评价解集只能从收敛性、多样性和均匀性三个方面来评价解集的好坏。下面是Generational Distance(GD)[12]评价指标的定义。 假设S是多目标优化问题的目标向量集合,P中的点均匀分布在整个理想的PF面上,GD计算S到P的距离,定义 (5) 其中,|S|表示集合S中元素的个数;GD表示的集合的收敛性,GD值越小表示收敛性越好。 改进的有效序值算法(Improved Prefer- ence Order Genetic Algorithm,IPOGA)主要的改进有以下3方面:(1)提出一种新的杂交算子(多边形杂交算子);(2)提出基于ε-占优的有效序排序方法;(3)提出新的计算拥挤度算法(超体积算法)。 在POGA算法中采用SBX[13]方式进行交叉,从父代中选出两个个体进行单点交叉。这种交叉算子虽然能够很好的保证解的质量,但是无法保证解的多样性。因此本文提出多变形杂交算子,对于m维的多目标优化问题,每次从最优解中选出m个个体构成一个多边形,计算出多边形的重心,然后以这个重心向外或者向内扩展构成新的多边形,最后在新的多边形上产生m个子代。如图1所示,A、B和C构成一个三角形,重心为G,对三角形进行向外扩张产生子代A2,B2和C2,向内收缩的方式产生子代A1,B1和C1。这样保证了每次通过向外扩或者向内收缩可以产生子代个体。 图1 三角形杂交算子 POGA算法[11]采用NSGA-II算法[14]的框架,对第一层非支配通过降维的方式,将 维不能比较的解降到m-1维进行比较。由于第一次层的解比较多,采用有效序值给第一层每个非支配分配一个有效序值,然后根据有效序值进行排序。但是由于同一有效序值的点比较少,故采用ε-占优的方式,即对每个目标值减去一个ε值,目的是为了让更多的解具用相同的有效序值,提高算法的收敛速度。算法如下: 步骤1对非支配解集P,解集的大小|P|=N,目标个数为m,每个解的有效序值k=1,且都是无效的efficient=0; 步骤2目标空间降到m-1维,对于任意一个m-1维的子空间,都存在一个同一的非支配解A,则解A的有效序值为k=k+1,且是有效的efficient=1; 步骤3由于k值相同的解比较少,对有效序值为k+1的解采用ε-占优,对每个目标值减去ε值,这样可以将有效序值为k+1的解的有效序值更改为k; 步骤4如果k 步骤5如果m-1>0,转移到步骤2,否则算法结束。 由于高维多目标优化算法中的的目标函数构成了一个空间,不是一个平面。因此空间解与解之间的拥挤度采用超体算法来计算,算法如下 步骤1非支配解集大小N=|P|,P为非支配解集,目标个数为M。 步骤2对属于P中每一个个体x,令其拥挤度为cd(x)=0。 步骤3对第m个目标,所有个体根据函数值进行排序,第一个和最后的一个的拥挤度为∞,即cd[1].m=dc[N].m=∞。 步骤5如果m=M,算法结束,否则转移到步骤3。 IPOGA算法的主要过程: 步骤1令t=0,初始化种群P(t),种群个数为N,目标个数为m; 步骤2计算P(t)中每个个体的适应度值; 步骤3将P(t)分成m份,从每份中选出一个采用多边形杂交算子进行杂交,最后生成N个子代; 步骤4对种群P(t)执行变异操作; 步骤5将原始种群的N个个体和新产生的N个个体结合产生2N个个体,对其进行改进的有效序值排序方法,从中选出N个个体。 步骤6若算法满足结束条件则结束,否则,令t=t+1,转移到步骤3。 为了验证IPOGA算法的有效性,本文选择文献[15]中的测试集试集DTLZ1~DTLZ2。通过实验证明算法的有效性。实验中设置种群的规模为100,运行10次,每次迭代300次。最后比较10次运行结果的平均(mean)值和方差(std)值。实验结果如表1~表4所示。实验通过比较IPOGA算法,POGA算法[12]和NSGA-II算法[14]的收敛性来验证IPOGA的算法的有效性。 表1 DTLZ1的GD mean的实验结果 表2 DTLZ1的GD std的实验结果 表3 DTLZ2的GD mean的实验结果 表4 DTLZ2的GD std的实验结果 从表1 可以看出对于DTLZ1测试集,IPOGA算法的GD mean值的效果全部都比POGA算法和NSGA-II算法好,说明IPOGA的收敛性比NSGA-II和POGA好。从表2 可以看出对于DTLZ1测试集,IPOGA算法的GD std值的效果基本全部都比NSGA-II算法和POGA算法好。但在目标维数为7时没有NSGA-II和POGA算法效果那么好,在目标维数为8时,比POGA算法好,但没有NSGA-II效果好。这说明了IPOGA算法的收敛性波动比较小。 从表3可以看出对于测试集DTLZ2,IPOGA算法的GD mean值基本比POGA算法和NSGA-II的算法GD mean 效果好,但是对于目标维数为4和8时,IPOGA算法的GD mean值没有其他两个算法的效果好。说明IPOGA跟POGA的收敛性基本差不多。 从表4可以看出对于测试集DTLZ2,IPOGA算法中的GD std值基本上都比POGA和NSGA-II算法中的GD std值效果相当。但是在目标维数为4和7时,IPOGA算法的GD std值的效果比POGA跟NSGA-II的算法好,但在其他目标维数数上的GD std值的效果就没有POGA算法好。 综上所述,在DTLZ1测试集中IPOGA算法的的收敛性明显优于NSGA-II算法和POGA算法。在DTLZ2的测试集上IPOGA算法的收敛性明显比NSGA-II算法的收敛性好,与POGA算法的收敛性基础保持一致。 本文对POGA算法进行改进,加入多边形杂交算子和基于ε-占优有效序值排序方法,能够较好地提高高维多目标算法的收敛压力,提高收敛速度。经过实验验证IPOGA确实能够提高算法的收敛性。后续工作将对本算法继续改进,使其更加有效的解决高维多目标优化问题。 [1] 丁岳伟,窦飞飞.多目标猫群优化算法支持下的云计算任务调度[J].电子科技,2016,29(2): 4-8. [2] 明丽洪,吕光宏,向虹佼.多QoS约束条件下的多目标网络优化[J].电子科技,2014,27(3):18-21. [3] Bechikh S,Elarbi M,Said L B.Many objective optimization using evolutionary algorithms:a survey[M].Germany:Springer International Publishing,2017. [4] 过晓芳.高维多目标优化算法研究综述[J].科技视界,2015(15):21-22. [5] Aguirre H,Tanaka K.Adaptive ε-Ranking on many-objective problems[J]. Evolutionary Intelligence,2009,2(4): 183-206. [6] Zhang Q,Li H.MOEA/D:A multiobjective evolutionary algorithm based on decomposition[J].IEEE Transaction on Evolutionary Computation,2007,11(6):712-731. [7] Li K,Deb K,Zhang Q,et al.An evolutionary many-objective optimization algorithm based on dominance and decomposition[J].IEEE Transactions on Evolutionary Computation,2015,19(5):694-716. [8] Li K,Kwong S,Zhang Q,et al. Interrelationship-based selection for decomposition multiobjective optimization[J].IEEE Transactions on Cybernetics,2015,45(10):2076-2088. [9] Deb K,Jain H.An evolutionary many-objective optimization algorithm using reference-point-based nondomi- nated sorting approach, part I: solving problems with box constraints[J].IEEE Transactions on Evolutionary Computation,2014,18(4):577-601. [10] Jain H,Deb K.An evolutionary many-objective optimization algorithm using reference-pointbased nondominated sorting approach, part II: handling constraints and extending to an adaptive approach[J].IEEE Transactions on Evolutionary Computation, 2014,18(4):602-622. [11] Di Pierro F,Khu S T,Savic D A.An investigation on preference order ranking scheme for multiobjective evolutionary optimization[J].IEEE Transactions on Evolutionary Computation,2007,11(1): 17-45. [12] Van Veldhuizen D A,Lamont G B. Multiobjective evolutionary algorithm test suites[C].France:Proceedings of the 1999 ACM Symposium on Applied Computing,1999. [13] Yu Z,Wong H S,Wang D,et al. Neighborhood knowledge-based evolu- tionary algorithm for multiobjective optimization problems[J].IEEE Transactions on Evolutionary Computation,2011,15(6):812-831. [14] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetical algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2): 182-197. [15] Deb K,Thiele L,Laumanns M,et al.Scalable multi-objective optimization test problems[C].Grace:Proceedings of the 2002 Congress on Evolutionary Computation,CEC′02,IEEE,2002. An Many-Objective Algorithm Based on Improved Effective Ordering XU Ning,WEI Jingxuan,ZHAO Long (School of Computer Science and Technology,Xidian University,Xi’an 710071,China) To overcome the shortcomings of the efficient ranking of many-objective optimization algorithm, an improved efficient ranking of many-objective optimization algorithm is proposed..A new recombination operat- or called polygon recombination operator is proposed by the algorithm in order to improve the diversity of the po- pulation,and a ε-dominance-based efficient ranking method is proposed in order to increase the convergence pres- sure and speed. Finally, the effectiveness of the algorithm is verified by the standard test functions. many-objective optimization; effective ranking; ε-dominance 2017- 03- 20 国家自然科学基金(61203372) 胥宁(1989-),男,硕士研究生。研究方向:智能计算。魏静萱(1981-),女,博士,副教授。研究方向:智能计算。 TN953;TP301.6 A 1007-7820(2018)02-029-041.2 高维多目标解集的评价指标
2 改进的有效序值算法
2.1 多边行杂交算子
2.2 基于ε-占优的有效序值算法
2.3 超体积算法
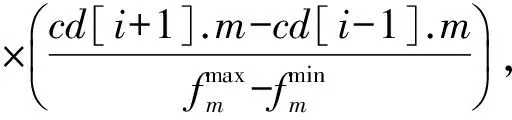
2.4 算法过程
3 仿真实验与结果分析
3.1 实验
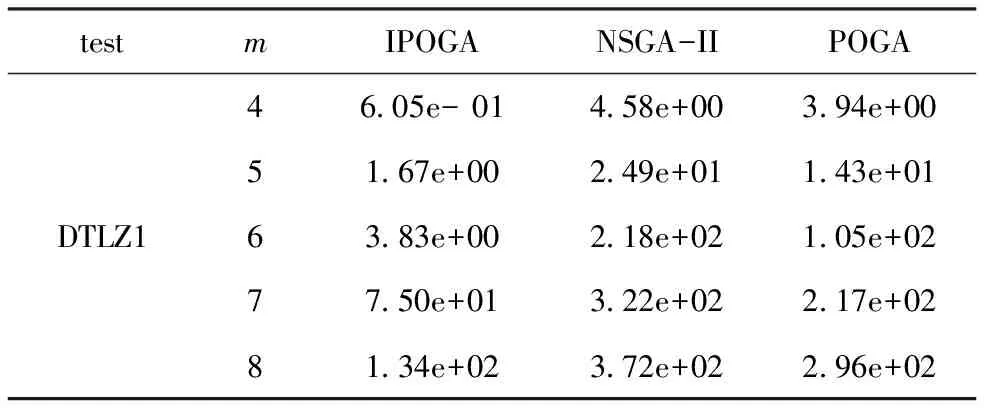

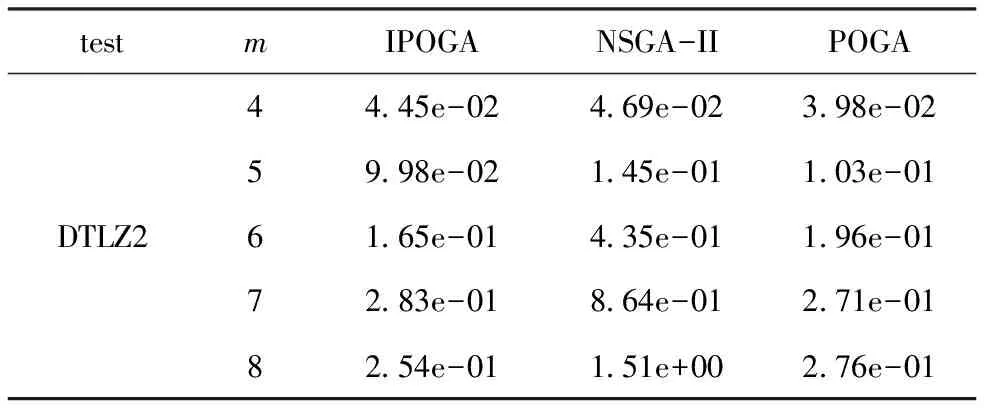
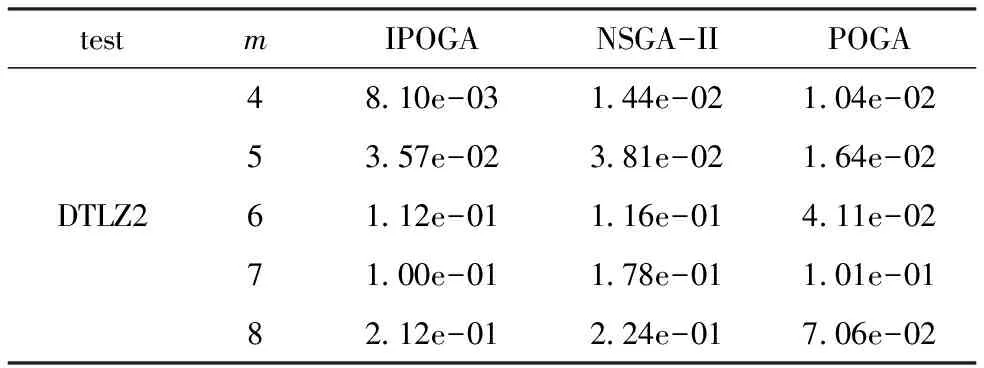
3.2 实验结果分析
4 结束语
