SH波的激发及与金属板中损伤相互作用

张超瑾，徐桂东

(江苏大学 理学院，江苏 镇江 212013)

SH波的激发及与金属板中损伤相互作用

张超瑾，徐桂东

(江苏大学 理学院，江苏 镇江 212013)

针对金属板中腐蚀损伤的检测，建立d36型压电晶片激发SH波及与损伤相互作用的有限元数值模型。利用d36型压电晶片激发的导波场数据，研究各模态导波的传播方向和幅值特征；通过比较SH0波和S0波与损伤相互作用的反射系数，讨论板中不同曲率与深度的腐蚀损伤对SH0波和S0波的传输响应。模拟研究表明：选择合适的激励频率能提高d36型压电晶片激发SH波的效率；与S0波相比，SH0波对腐蚀损伤具有更高的敏感度。研究结果为金属板材中腐蚀损伤的高灵敏度检测提供了参考。

腐蚀损伤；SH波；反射系数；有限元法

相比传统的体波损伤检测，超声导波具有传播距离远，能量损失低等优点已成为当前结构健康监测/无损检测领域的研究热点。在薄板结构中，导波可分为Lamb波和水平剪切( Shear Horizontal，SH)波。其中Lamb波已有多项研究成果用于损伤检测[1-2]，然而其固有的多模态和色散等特征使得接收信号的解读具有一定的挑战。相比于Lamb波，SH波在频率低于其一阶截止频率时，具有模态单一且在各向同性板内无色散的优点。因此SH波在超声无损检测领域极具研究价值。

基于SH波的各类结构损伤检测已经取得一系列研究成果，如焊接处[3]和复合梁结构中[4]损伤的检测，换能器与待测结构间连接状况的判断[5]。传统的SH波激发通常使用电磁声换能器(EMAT)，但有研究表明待测结构的导电性能会限制EMAT的激发效率[6]。压电换能器激发导波无需材料具有导电性，因此成为无损检测领域的又一大研究热点。一类由12片d24型压电晶片组成的换能器实现了全方位激励幅值相等的SH波[7]。在特定方向极化d36型压电单晶弛豫钛酸铅，能提高压电激发SH波的效率[8]。深入探究d36型压电晶片在板中与管道中激发/传感导波的能力，验证了d36型压电材料的高机电耦合效率[9-11]。由上述研究可知d36型压电晶片能够高效激发SH波，但对其激发的方向性及损伤检测的应用却鲜有研究。

本文基于压电效应和SH波的传播理论，利用有限元数值模拟分析d36型压电晶片激发SH波的特征和SH波检测腐蚀损伤的能力。讨论激发效率与信号频率的关系以及激发出的导波场分布特征，提出SH波的优化激发方案。在此基础上研究SH波对不同尺寸腐蚀损伤的传输响应，通过比较损伤对SH0波和S0波的反射系数，评估SH波检测腐蚀损伤的可行性。

1 理论分析

1.1 d36型压电单晶

根据压电效应，压电材料的应变和电位移由所受的应力和电场两部分影响叠加组成[12]。从上世纪末Park等人首次制备出弛豫压电单晶起，其优异的压电性能就受到广泛的关注。在众多弛豫晶体的改良体中，有一类d36型压电单晶的机电耦合系数k和压电系数d33分别达到90%和1 500 pC/N。且在[0,1,1]方向极化该材料并以极化方向为轴旋转45°后，材料的压电参数d36高达1 648 pC/N。压电系数d36在正压电效应下表现为受到面内的剪应力σ12时，压电晶片表面会累积电荷形成电信号；在逆压电效应中则表现为在厚度方向加电场时压电晶片会产生剪切形变响应。根据压电双向耦合效应，d36型压电晶片可实现SH波的激发和接收。

1.2 有限元参数及材料参数设定

有限元数值模拟建立在严密的数学理论计算基础上，能够处理复杂的几何模型并得到精确解。使用有限元瞬态数值模拟分析板中的导波场必须充分考虑反射波的影响。因此设定模型几何尺寸时应结合频散曲线给出的波速条件，尽量降低反射波场对原波场的干扰。时间步长和网格大小的设定需要兼顾计算的效率和精度，应分别小于1/20f和最小波长的1/10[13-15]。利用有限元仿真软件Comsol Multiphysics数值模拟d36型压电晶片在金属铝板中激发出的导波场，为提高金属板中SH波激发效率提供理论依据。数值模拟中的金属铝杨氏模量为71.0 GPa，泊松比为0.33，密度为2 700 kg/m3。压电晶片材料为d36型压电弛豫单晶，压电参数矩阵和柔度矩阵已在文献[7]中给出。

2 数值模型、结果与讨论

2.1 d36激发导波场模型

在压电模块下构建尺寸为100 mm ×100 mm × 1 mm三维铝板模型，在板上表面中心处放置尺寸为10 mm ×10 mm × 0.5 mm的d36型压电晶片。在以压电晶片为中心，半径R=20 mm绘制的圆上每隔5°取一个点，共计72个接收点构成接收点列。取径向，切向和离面方向建立坐标系并分析d36型压电晶片激发的各模态波在板状结构中的分布特征。根据Lamb波和SH波的定义可知Lamb波由径向位移dr和离面位移w构成，SH波只由切向位移dτ构成。根据矢量合成法则得出径向位移，切向位移与x方向位移分量u，y方向位移分量v，z方向位移分量w的关系如下

dr=ucosθ-vsinθ
dτ=vcosθ+usinθ

(6)

其中，θ为波的传播方向(即径向)与x轴正半轴的夹角。

将幅值为10 V的五峰波脉冲作为激励信号源，扫描频率范围在100～400 kHz，步长为20 kHz。按照模拟参数设定标准，设定压电晶片的最大网格尺寸为0.25 mm，铝板的最大网格尺寸为0.5 mm。瞬态求解器的时间步长设定为0.1 μs，终止时间设置为15 μs。

在每个频率点上提取点列中的最大切向位移值，绘制频率和切向位移归一化幅值的关系如图1。图中显示激励信号中心频率在220 kHz附近时切向位移取到极大值，表明此时SH波的压电激发效率最高。

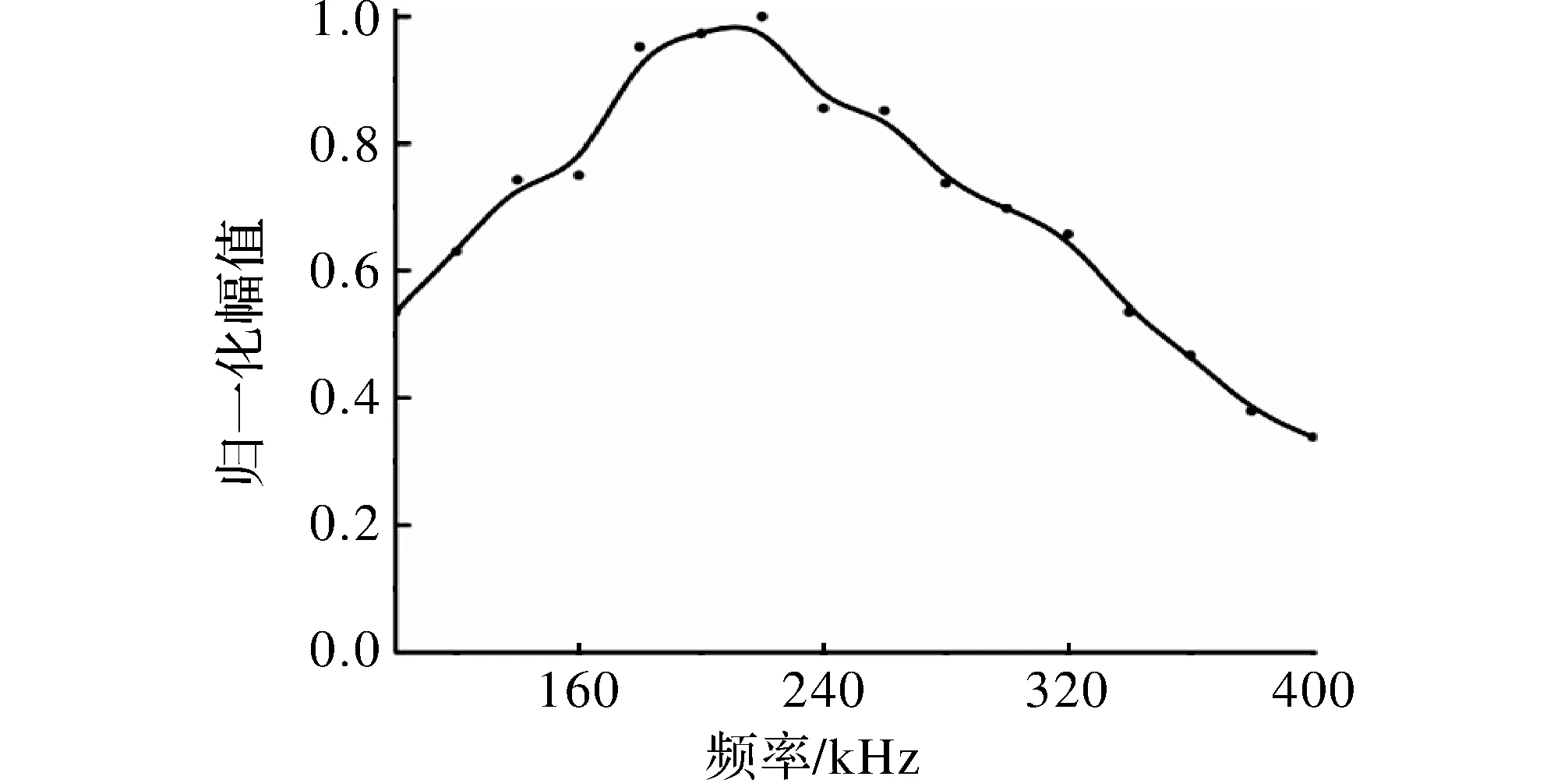
图1 100～400 kHz范围内的切向位移归一化幅值图

图2给出220 kHz时接收点列上不同波包的位移值，包括S0波包的径向位移，SH0波包的切向位移和A0波包的离面位移幅值。利用频散曲线中各模态波速的差异，将导波场按模态区分，便于深入探究d36型压电晶片的激发特性。研究表明Lamb波主要沿45°和225°方向传播，关于y=x和y=-x呈轴对称状态；而SH波在板中主要沿坐标轴方向传播且在4个象限中的分布完全一致。通过重现板中各模态波的分布，分析并实现SH波的高效激发。

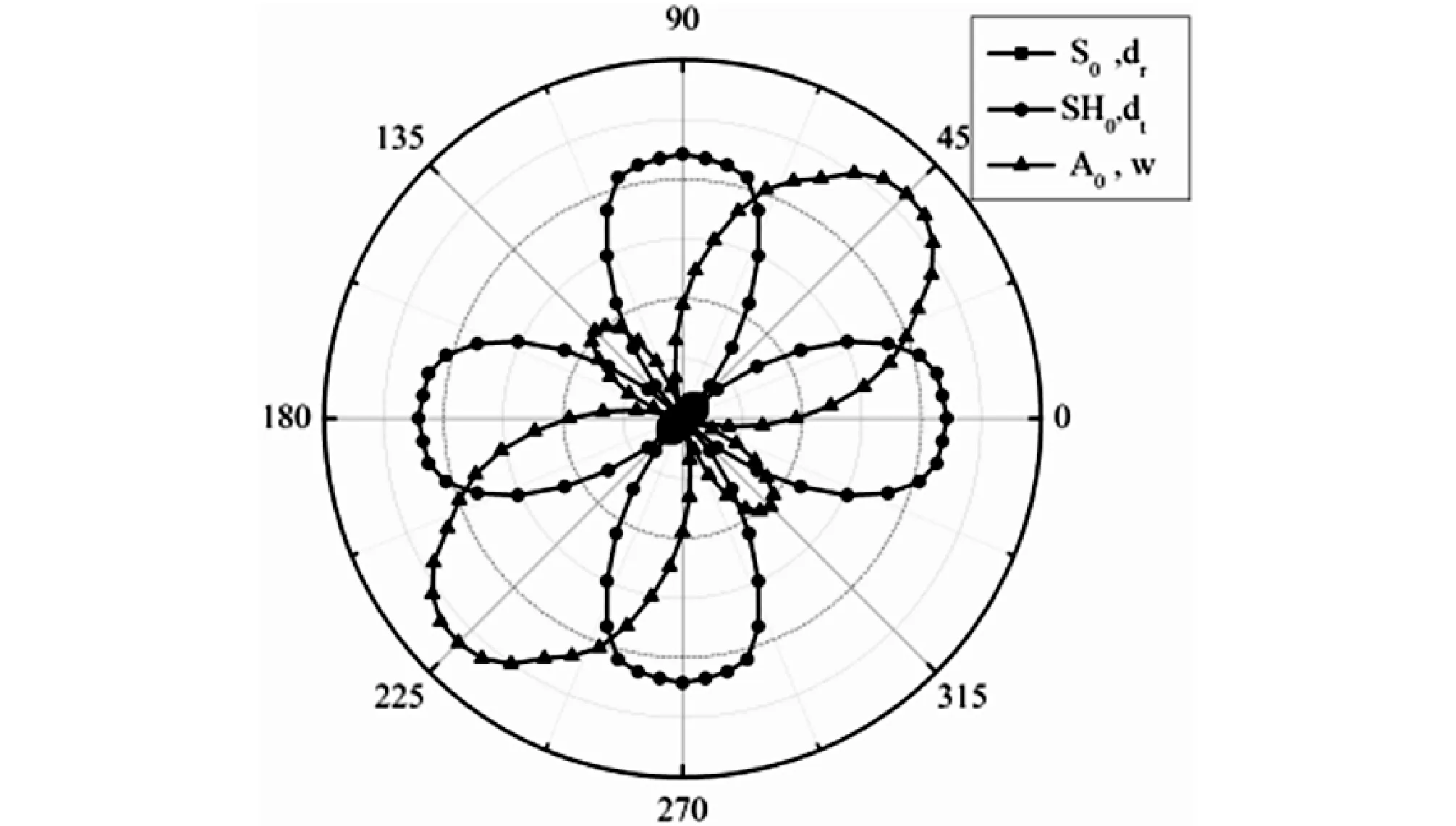
图2 S0,SH0,A0模态在不同传播方向上的位移相对幅值

利用有限元数值模拟方法提取并分析d36型压电晶片激发的导波场，描述各模态导波的空间分布特征，为d36型压电晶片高效激发SH波提供参考。

2.2 SH波与腐蚀损伤相互作用

为研究SH波与腐蚀损伤的相互作用。在150 mm×120 mm×1.6 mm的铝板上表面x=0 mm，y=60 mm处放置3 mm×3 mm×0.5 mm的方形的d36型压电晶片，激励信号是中心频率220 kHz，幅值10 V的五峰波脉冲信号。依据对称性取x=0为对称面，以半板模拟全板内的波场分布。图3(a)是SH波与腐蚀损伤数值模拟的三维模型示意图，损伤中心O点的坐标为(70, 60, 1.6) mm，图3(b)是腐蚀损伤的剖面示意图，损伤的曲率半径为R，损伤深度和板厚度分别为t和d，在波的传播方向上取一接收点，坐标为(90, 60, 1.6) mm。按有限元参数设定标准，将网格尺寸和时间步长分别设定为0.9 mm和0.2 μs。

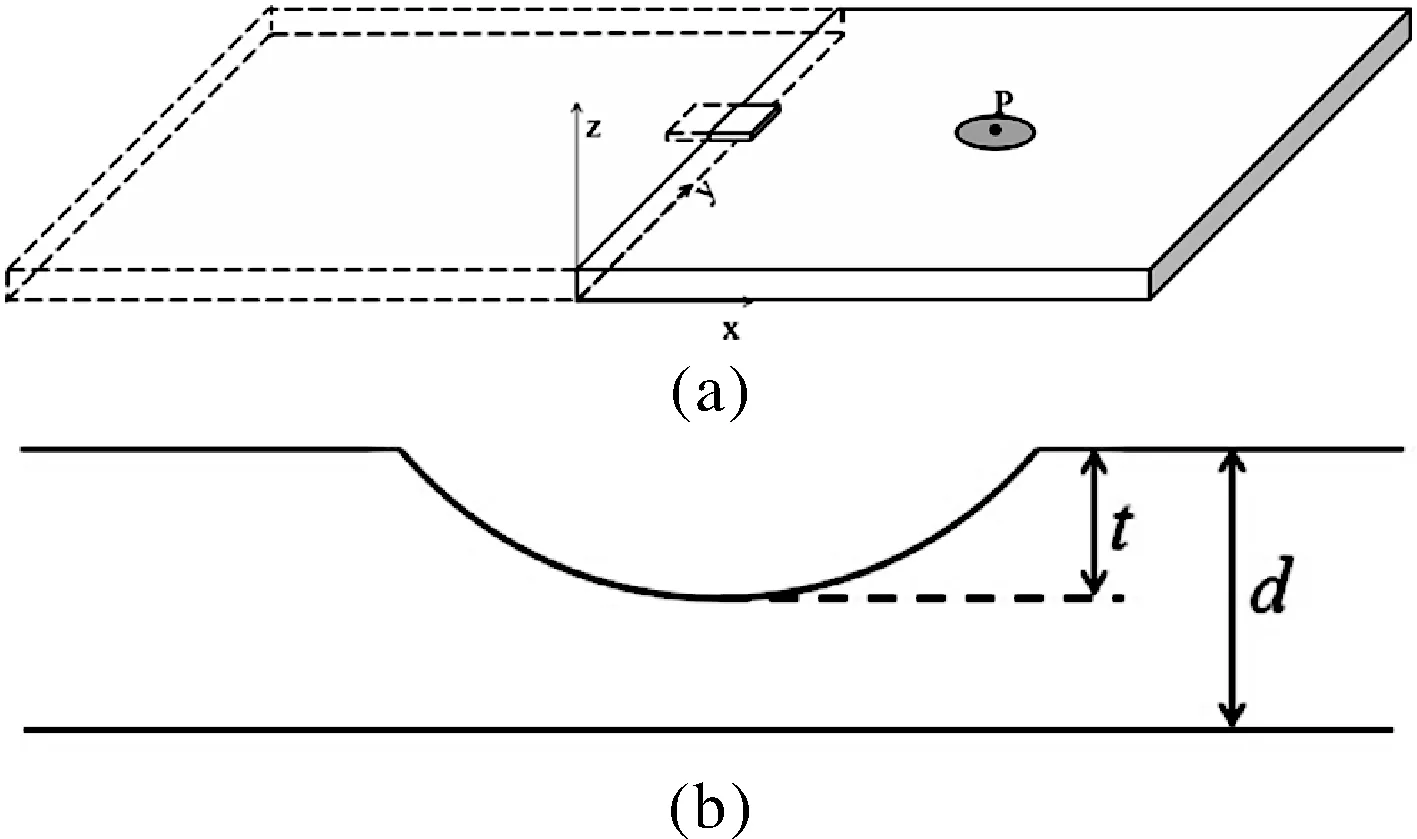
图3 铝板中腐蚀损伤和腐蚀损伤剖面示意图

图4给出不同曲率半径腐蚀损伤对SH0波和S0波的反射系数，由图可见不同曲率半径的腐蚀损伤对SH0波的反射系数总是高于S0波，验证了SH0波检测腐蚀损伤的能力。此外，在频率不变时扩大损伤曲率半径R，损伤对SH0波和S0波的反射系数均明显增加。结果表明SH0波和S0波经损伤反射后，反射波场均携带了腐蚀损伤的曲率半径信息。

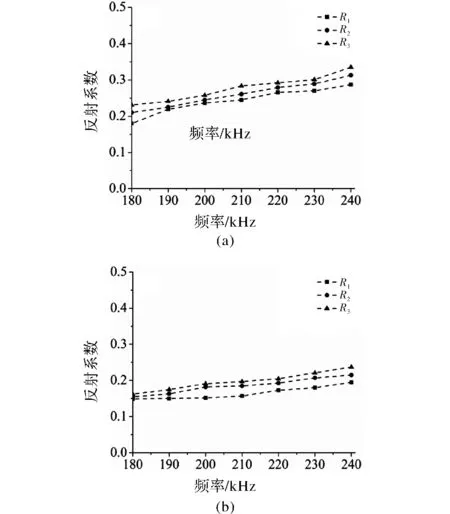
图4 腐蚀深度t=d/2，曲率半径R1=7.08 mm,R2=8.02 mm,R3=9.16 mm时，SH0波和S0波对腐蚀损伤的反射系数

图5显示不同深度腐蚀损伤对SH0波和S0波的反射系数，表明损伤对SH0波的反射明显强于S0波。随腐蚀损伤的加深，SH0波的反射系数增长速度明显快于S0波(约为S0波的4倍以上)，这表明相比S0波，SH0波在经腐蚀损伤反射后携带的损伤信息更能反映出腐蚀损伤的深度变化。

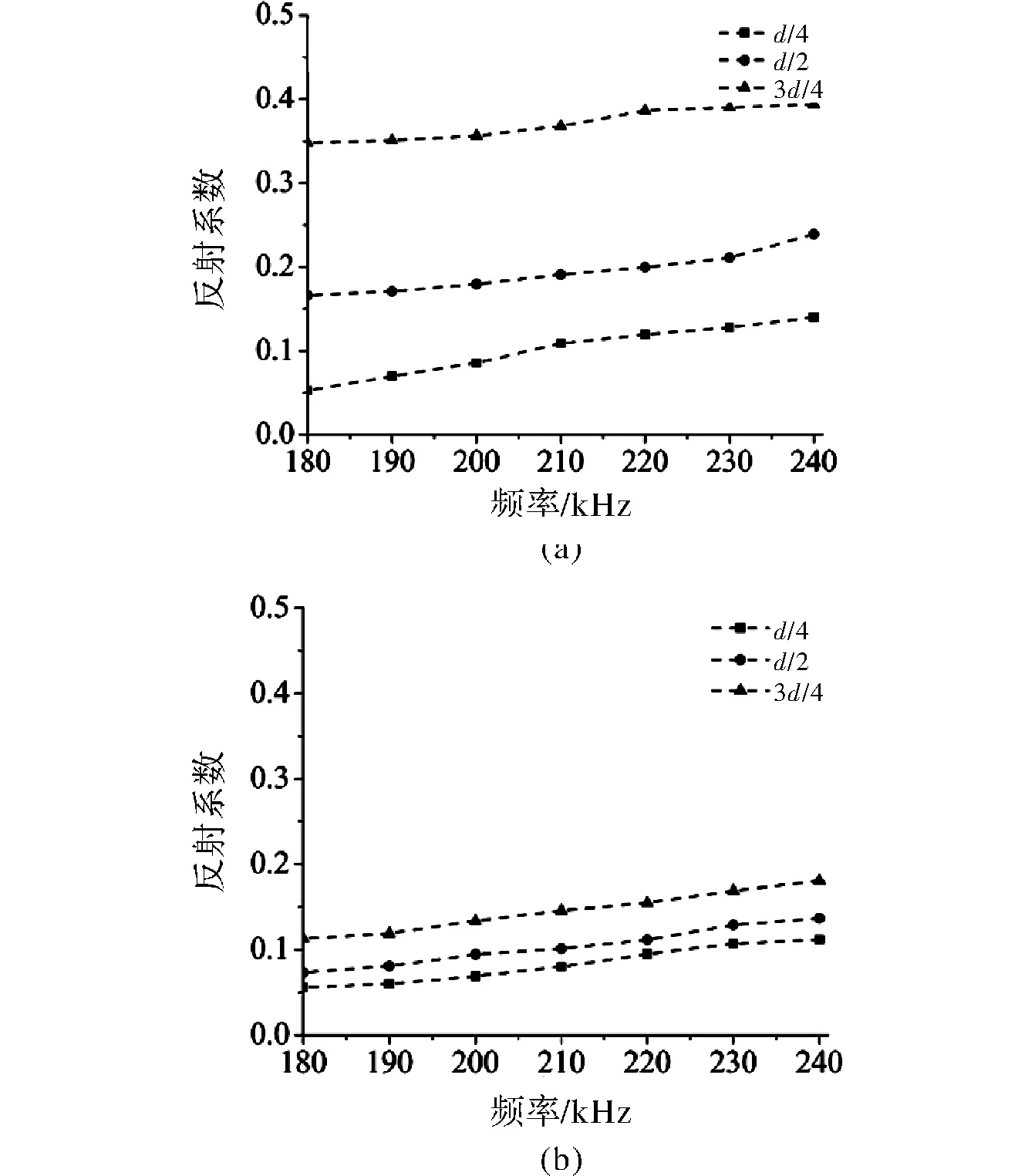
图5 腐蚀曲率半径R=9.16 mm，深度t=d/4,d/2,3d/4时，SH0波和S0波对腐蚀损伤的反射系数

3 结束语

本文建立了两个有限元数值模型：(1)d36型压电晶片激发导波场数值模型；(2)SH波与腐蚀损伤相互作用数值模型。在第一个模型中通过频率扫描找到SH波最高压电耦合效率的频率点，提取位移场信息并分析所激发导波在空间的分布特征，实现了d36型压电晶片在金属铝板SH波的高效激发。在第二个模型中模拟SH波与腐蚀损伤的相互作用，提取损伤在不同曲率半径和深度下的反射波信息，分析腐蚀损伤尺寸对SH0波和S0波的影响程度。数值模拟结果表明SH0波能用于腐蚀损伤的存在性检测，为高敏感度的腐蚀损伤定量检测提供指导。

[1] Leleux A,Micheau P,Castaings M.Long range detection of defects in composites plates using Lamb waves generated and detected by ultrasonic phased array probes[J].Journal of Nondestructive Evaluation,2013,32(2):200-214.

[2] Ghadami A,Behzad M,Mirdamadi H.A mode conversion-based algorithm for detecting rectangular notch parameters in plates using Lamb waves[J].Archive Applied Mechanics, 2015,85(6):793-804.

[3] Lee J,Kim D.Integrity evaluation of pipe welding zones using wavelet transforms, and Specific Sensitivities based on SH-EMAT pulse-echo method[J].International Journal of Precision Engineering and Manufacturing,2014,15(10):2051-2057.

[4] Su Z,Yang C,Pan N,et al.Assessment of delamination incomposite beams using shear horizontal (SH) wave mode[J].Composites Scienceand Technology,2007,67(2):244-251.

[5] Le Crom,Castaings M.Shear horizontal guided wave modes to infer the shear stiffness of adhesive bond layers[J].Acoust Society of America,2010,127(4):2220-2230.

[6] Gao H,Ali S,Lopez B.Inspection of austenitic weld with EMAT[J].Review of Progress in Quantitative Nondestructive Evaluation 29B,2010,12(11):1175-1181.

[7] Miao H,Huan Q,Wang Q.A new omnidirectional shear horizontal wave transducer using face-shear (d24) piezoelectric ring array[J].Ultrasonics,2017,74(5):167-173.

[8] Zhang S,Jiang W,Meyer R J.Measurement of face shear properties in relaxor-PbTiO3single crystals[J].Applied Physics,2011,110(6):064106-064120.

[9] Zhou W S,Li H,Yuan F G.Guided wave generation, sensing, and damage detection using in-plane shear piezoelectric wafer[J].Smart Materials and Structures,2014,23(1):015014-015023.

[10] Zhou W,Li H,Yuan F.Fundamental understanding of wave generation and reception using d36type piezoelectric transducers[J].Ultrasonics,2015,57(7):135-143.

[11] Zhou W,Li H,Yuan F.Guided torsional wave generation of a linear in-plane shear piezoelectric array in metallic pipes[J].Ultrasonics,2016,65(3):69-77.

[12] Ayman K A.Ultrasonics transduction in metallic and composite structures for structural health monitoring using extensional and shear horizontal piezoelectric wafer active sensors[D].Carolina:University of South Carolina,2014.

[13] 许伯强,刘洪凯,徐桂东,等.基于应力-位移混合有限元法的激光超声数值模拟[J].激光技术,2014,38(2):230-239.

[14] 许伯强,张景秀,徐桂东,等.金属梁结构表面微损伤的谱有限元分析[J].电子科技,2015,28(12):5-9.

[15] 许伯强,来锴,徐桂东,等.复合层合梁层裂损伤与超声导波的相互作用研究[J].电子科技,2015,28(11):55-60.

SH Wave Generation and Interaction with Defects in Metallic Plates

ZHANG Chaojin,XU Guidong

(School of Science,Jiangsu University,Zhenjiang 212013,China)

Finite element modeling is built for SH wave generation of d36type piezoelectric wafer and its interaction with corrosion defects in metal plates. Utilizing the data extracted from the guided wave field generated by d36type wafer, directions of propagation and amplitudes for various modes are studied. Reflection coefficients of SH0and S0waves are compared to discuss transmission response to corrosion defects in various radius and depth. Simulation results imply that appropriate excitation frequencies can improve excitation efficiency of SH wave and compared with S0wave, SH0wave is more sensitive to corrosion defects. It provides theoretical basis for high-sensitivity corrosion defects detection in metallic plates.

corrosion defects; shear horizontal wave; reflection coefficient; finite element method

2017- 03- 29

江苏省六大人才高峰基金(2012-ZBZZ-027)

张超瑾(1989-)，男，硕士研究生。研究方向：压电超声无损检测。徐桂东(1976-)，男，实验师。研究方向：超声无损检测与评价。

TN04；O426

A

1007-7820(2018)02-008-04