复合摆和耦合摆运动的可视化
2018-01-06周成博宋一诺范光华
周成博 宋一诺 范光华,1)
∗(威海市第一中学,山东威海264207)
†(哈尔滨工业大学 (威海)光电科学系,山东威海 264209)
复合摆和耦合摆运动的可视化
周成博∗宋一诺†范光华†,1)
∗(威海市第一中学,山东威海264207)
†(哈尔滨工业大学 (威海)光电科学系,山东威海 264209)
利用视频跟踪技术和Tracker软件,通过运动时序图和李萨如图展示了不同数量复合摆构成的耦合摆的多种运动形式,包括两个复合摆的同振幅同方向振动、同振幅反方向振动、拍振以及3个和4个摆之间的能量转移运动.这种实验演示方法有助于学生加深对耦合摆运动规律的认识.
复合摆,耦合摆,视频跟踪技术
在高中和大学物理课中,单摆的摆动经常用做简谐振动的模型.单摆在平衡位置两侧的来回摆动很直观地表现为周期性运动.但是,单摆偏离平衡位置两侧的角度或幅值随时间的变化,也就是简谐振动,却不容易构思.此外,实际情况下还存在各种形式的复杂振动,它们都是各种简谐振动的耦合或叠加[1],其运动形式比较复杂,规律不够直观,初学者对这些方面知识的理解存在一定困难.由于单摆的摆线是柔性的,单摆之间的耦合受到一定的限制.复合摆的运动形式跟单摆类似,刚性摆杆一端连接摆锤,另一端可以绕一个轴转动,摆杆之间可以方便地通过弹簧或橡皮筋实现耦合[23].因此,多个复合摆之间可以实现多种形式的耦合运动.以往的教学论文中,已经通过各种手段实现多种振动的可视化[415].这些实验装置都有很多优点,但是缺点在于要么不适合在学生很多的场合展示.要么需要采用比较复杂的电路将运动信号转换为电信号,并且需要频率范围合适的示波器或其他仪器进行演示,对仪器设备要求较高,因此不易实现.
近年来,随着信息技术的发展,目标视频跟踪已经很容易实现.利用手机可以拍摄各种运动的视频,利用软件技术可以实现运动物体的视频捕捉和运动跟踪,再利用软件的后续处理,可以得到运动物体的轨迹、振幅(摆角)以及相位随时间的变化规律[1618].这些通过跟踪物体运动视频,并利用软件处理得到物体运动的变化关系图的方式,可以使学生更好地理解和掌握所要研究学习的运动的规律,具有重要意义.由多个复合摆组成的耦合摆具有多种运动形式,是关于简谐振动和耦合运动的典型范例,目前缺乏关于这些运动的形象的展示手段.本文利用手机拍摄复合摆和耦合摆的视频,利用开源软件Tracker实现视频中被观察物体的运动跟踪,获取其摆幅随时间的变化曲线,通过不同复合摆摆幅之间的关系曲线,全面展示复合摆和耦合摆的多种运动形式,为学生学习这方面的知识提供有价值的资料.
1 实验装置和实验细节
复合摆和耦合摆的实验装置如图1(a)所示,摆锤通过刚性摆杆连接在转轴上,利用弹簧连接复合摆的摆杆,可以在复合摆之间形成耦合作用从而构成耦合摆.耦合摆中的复合摆数量可以不受限制,图1分别为两个、三个和四个复合摆通过弹簧构成的耦合摆.本实验的每个复合摆完全一样,摆锤重686.5g,摆杆重132.2g,耦合长度为50cm,通过调整摆锤上方的扁平螺母,可以小幅改变复合摆的摆动周期,以实现现象比较显著的拍振.实验过程中用手机录取所有摆的运动视频,在电脑中用Tracker软件对视频进行处理,获得有关运动曲线.在摆锤上贴不同的标签,以利于视频跟踪和Tracker软件后续数据处理.

图1 复合摆构成的耦合摆
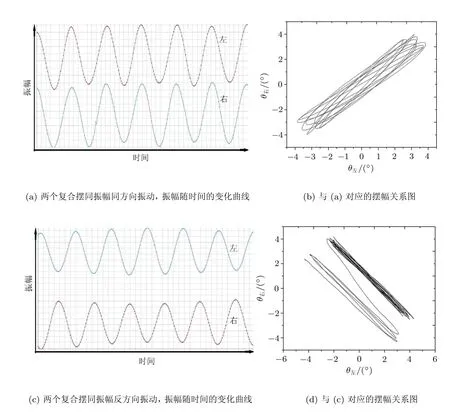
图2 两个复合摆耦合的时序图和振幅关系
2 耦合摆的实验观测与研究
2.1 两个复合摆的耦合运动
把两个复合摆的摆锤从平衡位置向同一个方向偏转相同角度,随后同时释放,耦合摆开始自由摆动.此情况下两个复合摆产生同方向振动.实验时,利用摄像头拍摄两个摆的运动视频,经过Tracker软件分析可获得不同时刻摆的角位移值.两个复合摆摆锤的角位移随时间变化的时序图如图2(a)所示,可以看出两摆频率基本相同,振幅几乎同时达到最大值 (或最小值).将左边摆的角位移值设置为横坐标,右边摆的角位移值设置为纵坐标,即可画出如图2(b)所示的李萨如图.严格意义上的李萨如图是某个运动质点在相互垂直方向做简谐振动的合成运动轨迹,图的横纵坐标分别对应于各个时刻该质点在相互垂直方向上的位移.在本论文中,为对耦合摆运动特点进行分析,构建的是耦合摆系统中某两个摆锤在各个时刻位移的非严格李萨如关系图.从图2(b)中可以看出所有的点基本上构成一条正斜率的准直线.仔细观察可以发现这些准直线略有弯曲,不是严格意义上的直线.其原因在于,在本实验的耦合摆装置中,为了观察比较明显的拍振动,已调整不同摆的周期值使其略有差别.在两个摆同振幅同方向振动时,尽管初始阶段两个摆之间的弹簧没有形变,但是随着振动的持续,两个周期略微不同的耦合摆之间还是会逐渐偏离同振幅状态,这使得两个摆之间的弹簧存在形变,从而使两个摆之间出现略微的耦合作用,在李萨如图中显示出来,因此出现图2(b)中略有弯曲的准直线.改变初始条件,把两个摆锤从平衡位置反方向偏转相同角度再同时释放,此情况下耦合摆产生同振幅反方向振动,运动的时序图如图2(c)所示,两个摆的频率相近而振动方向相反.两摆摆幅的李萨如图形如图2(d)所示,这些点最终会趋近于一条负斜率的直线.再改变初始条件,固定一个复合摆,把另一个复合摆拉离平衡位置,然后同时释放,此情况下耦合摆出现拍振,其运动形式是一个摆振幅达到最大的同时另一个摆的振幅最小,如此交替进行.从时序图上可以明显看出拍振的曲线,如图2(e)所示,图2(f)是拍振动的李萨如图形.

图2 两个复合摆耦合的时序图和振幅关系(续)
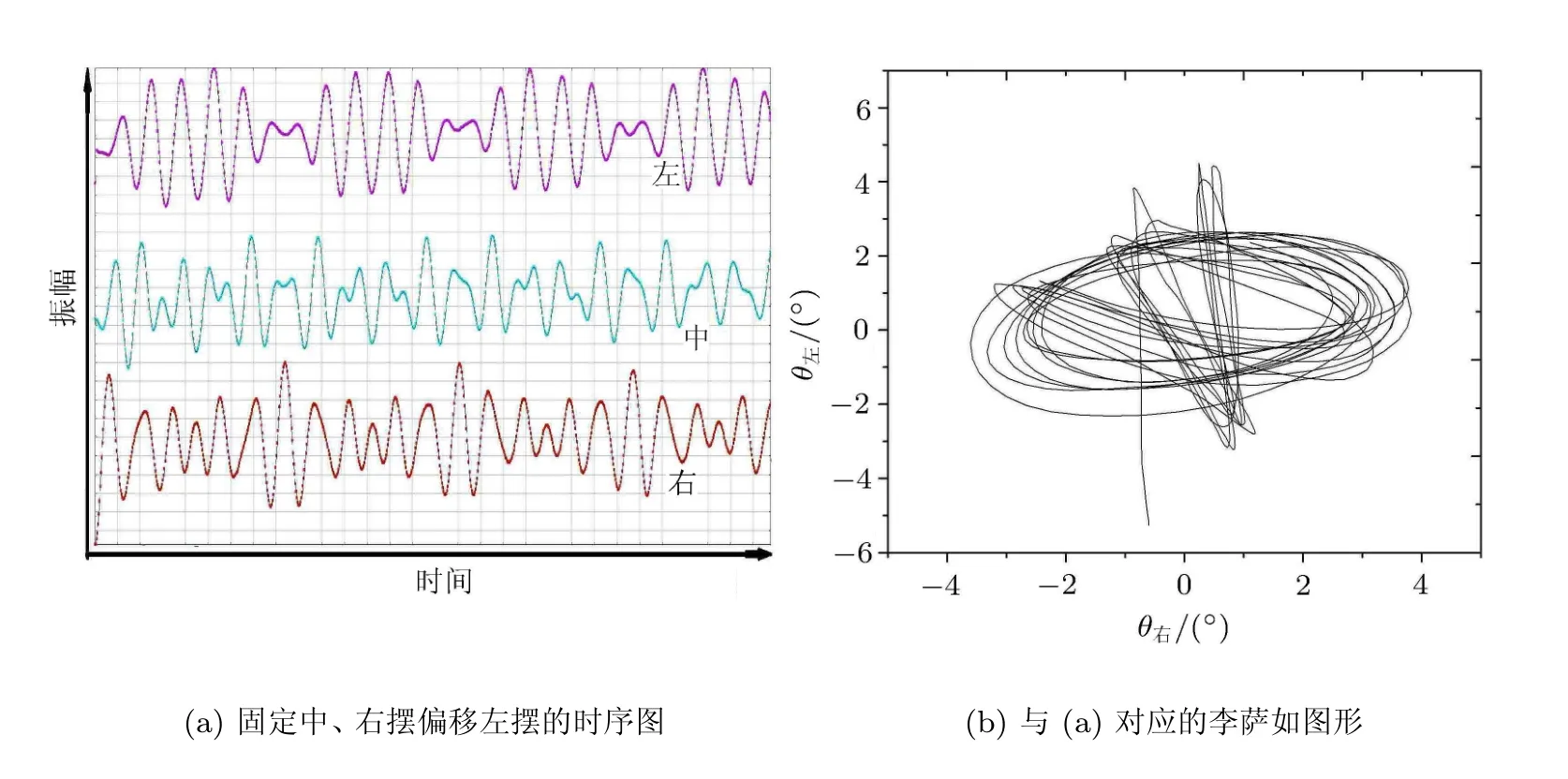
图3 三个复合摆耦合实验时序图及振幅关系图
2.2 三个复合摆的耦合运动
在三个复合摆耦合的情况下,把从左至右排列的 3个摆分别称为左、中、右摆.先固定中、右两摆,偏移左摆,然后同时释放三个摆,起初左摆振幅最大,随后其振幅衰减至最小,同时中摆振幅增至最大,而后中摆振幅逐渐衰减至最小而右摆振幅增至最大,之后这一现象又会从右到左依次进行.从图3(a)可以看出当一个摆振幅达到顶峰时另外两摆的振幅均为最小.其原因是机械能按照左→中→右→中→左的顺序不断传递,从而引起振幅的不断变化.图3(b)是左、右两摆的摆幅关系图,图中的点构成一个闭合的椭圆. 可以看到随着时间的增加,椭圆的旋转方向首先是顺时针,然后变为逆时针,再变为顺时针,再变为逆时针,如此交替变化.当椭圆的轴线平行于某个坐标轴时,反映在此椭圆对应的循环过程中某个摆的位移及其绝对值连续发生显著变化,而另一个摆的位移及其绝对值则只是发生小幅变化,这对应着拍振的运动形式.当椭圆的轴线与坐标轴倾斜时,反映在此循环过程中两个摆的位移及其绝对值连续发生显著变化,这对应着能量从一个摆向另一个摆转移的运动形式.当固定左、右两摆偏移中间摆时,又会产生另外一种运动:左右两摆发生同相同步,振幅同步增减且摆动方向一致,当中摆振幅最大时,左右两摆振幅最小,中摆振幅最小时,左右两摆振幅最大.从图 3(c)的振幅变化可以观察到此现象.图3(d)是左、中两摆的振幅关系,其变化规律类似图3(b).当固定左、中两摆偏移右摆时,由于对称性其现象与固定中、右两摆偏移左摆类似,不做重复描述.

图3 三个复合摆耦合实验时序图及振幅关系图(续)
2.3 四个复合摆的耦合运动
在四个复合摆耦合的情况下,把从左至右的四个摆依次编号为 1,2,3和 4,给予不同的初始条件,它会相应地产生多种运动.首先仿照上节所述的初始条件,固定摆2,3,4的同时将摆1偏离平衡位置,然后一起释放令其自由运动.四个摆产生与三个摆类似的运动情况:起初摆1振幅最大,在其逐渐减小的同时摆2的振幅增至最大,伴随摆2振幅减小摆3振幅又增至最大,一直传递到摆4之后又开始反方向进行该过程.即机械能按照 1→2→3→4→3→2→1的顺序在复合摆之间来回传递.从4(a)中的时序图可见,四个摆的运动方式都是一种拍振,当一个摆的振幅达到最大时,另外三个摆的振幅均在最小值附近.图 4(b)是任意两个相邻摆的摆幅关系图,其变化规律与图3(b)类似.
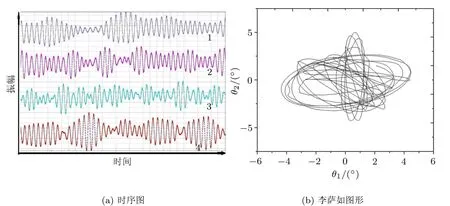
图4 四个复合摆耦合实验
接下来进行固定某两摆不动,拉开另外两摆,再同时释放的实验,这种实验有多种组合.其一,固定摆2和4使之保持不动,将摆1和3反方向拉开相同的偏角,然后同时释放,可以发现摆1和3为一组,摆2和4为一组,两组摆进行反相振动.当摆1和3的振幅达到最大时,摆2和4的振幅最小,之后摆1和3的振幅逐渐衰减至最小,而摆2和4的振幅逐渐增至最大.该运动的时序图以及摆1和2的李萨如图形如图5(a)和图5(b)所示.其二,固定摆 1和 4不动,将摆 2和 3反方向偏移相同角度后同时释放,所产生的运动现象与上一个实验类似,即摆1和4为一组,摆2和3为一组,两组摆进行反相振动,前一组摆的振幅最大时后一组摆的振幅最小.该运动的时序图以及摆1和2的李萨如图形如图 5(c)和图 5(d)所示.其三,固定摆 1和2,反方向偏转摆3和4再同时释放,实验现象也与上述现象相似,该运动的时序图以及摆1和3的李萨如图形如图5(e)和图5(f)所示.其四,固定摆1和4,将摆2和3同方向偏转相同的角度然后同时释放,可见摆1和4为一组,摆2和3为一组,两组摆进行同相振动,当摆1和4摆振幅达到极大值时摆2和3的振幅最小,该运动的时序图以及摆1和2的李萨如图形如图5(g)和图 5(h)所示.其余组合的同相振动类似,不做重复描述.
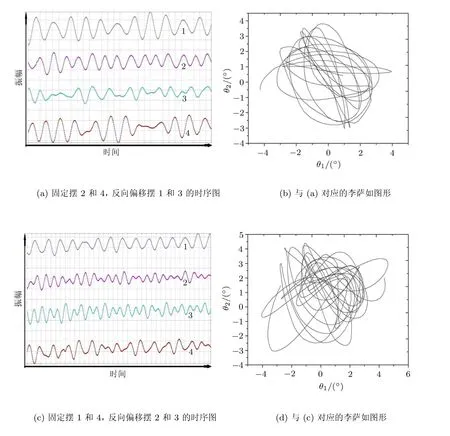
图5 四个复合摆耦合实验时序图及振幅关系图
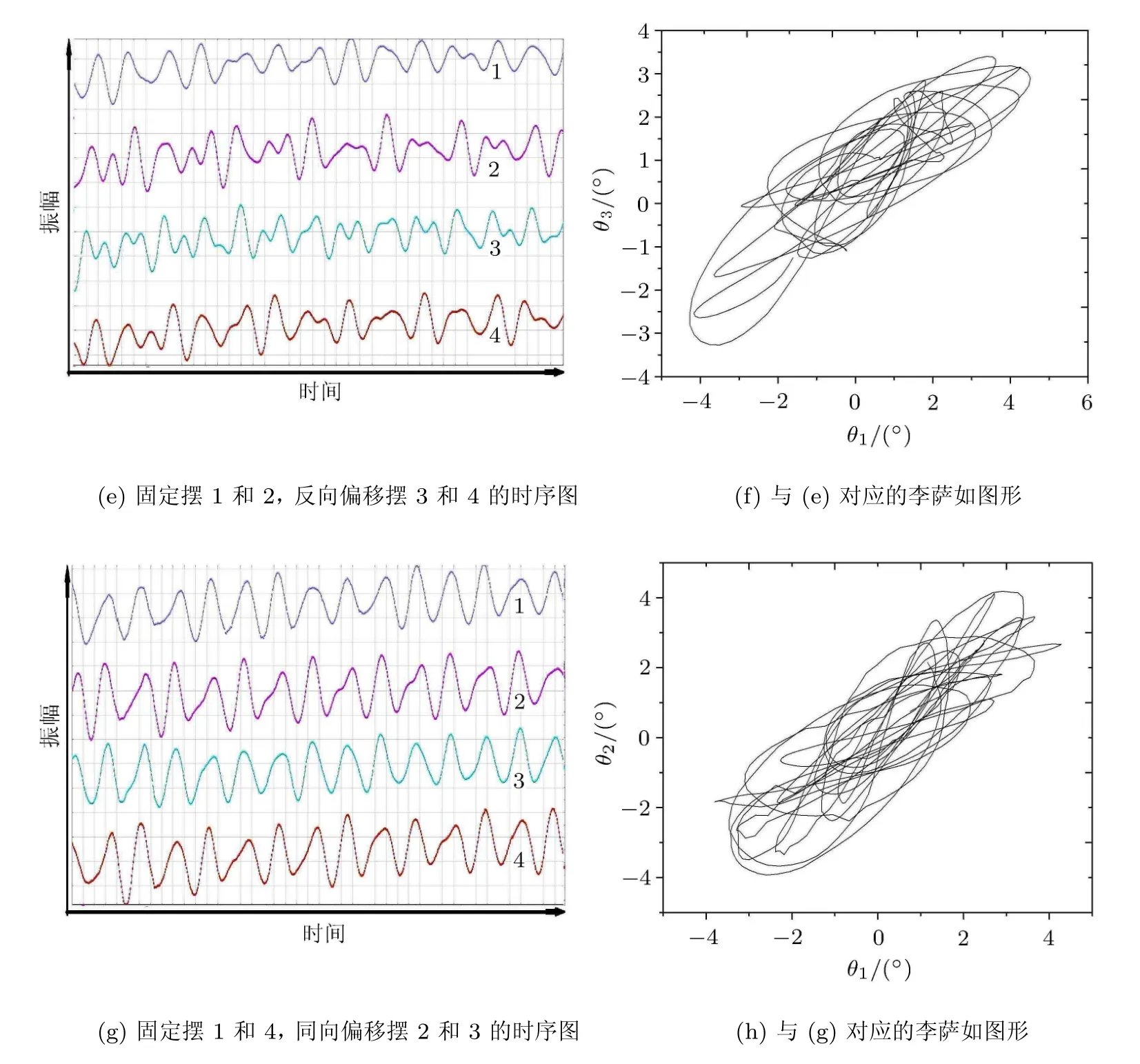
图5 四个复合摆耦合实验时序图及振幅关系图(续)
3 实验结论
利用视频跟踪技术和 Tracker软件,通过运动时序图和李萨如图形展示了不同摆动的形式.发现4个摆耦合运动的规律:初始偏移平衡位置的两个摆形成一组,按照与它们的初始条件相同的形式进行运动(初始反向偏移则反相振动,初始同向偏移则同相振动),而初始固定的两个摆形成一组,以同样的状态运动.这两组摆中的一组振幅最大时另一组的振幅最小,从李萨如图中可以看出它们产生拍振和能量的转移.这些实验有助于学生更好地理解简谐振动和耦合振动.
1陈清梅,颜素荣,安红.一种新的“弹簧振子--单摆”耦合摆研究.力学与实践,2008,30(6):93-95
2刘立宝,王本阳,李盛凤等.大学物理实验(上).安徽:安徽科学技术出版社,2010
3王文春,向鹏,包爱东.三体耦合物理摆振动研究.物理实验,1998,19(2):6-8
4宋燕盛,孙铁军.双、单摆振动示波装置.物理实验,1994,15(6):272-274
5曲忠峰,王佳海,刘继家.简谐振动图像演示仪.物理实验,2001,22(6):33-33
6熊宝库,冯一兵,冀晓群.弹簧振子振动图象的演示方法.物理实验,2004,24(6):29-29
7苏启录.单摆运动的实时测量.物理实验,2007,27(9):29-32
8朱向阳,施国富.单摆的振动图像演示装置.物理实验,2008,28(6):28-30
9程敏熙,曾碧芬,刘惠娜等.周期性外力驱动的混沌摆.物理实验,2009,29(1):7-13
10葛宇宏.单摆振动实时演示仪的制作与使用.大学物理实验,2009,22(2):69-72
11姚盛伟,徐平.耦合摆特性模拟及振动耦合现象演示.大学物理,2012,31(4):28-31
12丁琪,史德俐,芦立娟.智能传感器在大学生物理实验中的应用.大学物理实验,2012,25(3):75-79
13张瑞志,夏雪琴.传感器和Origin7.0软件在电脑控制韦伯福斯摆的实验研究中应用.大学物理实验,2013,26(4):82-85
14许生慧,钱仰德.受迫振动阻尼复摆实验仪.物理实验,2016,36(10):11-14
15荀坤.周期性弦链系统振动模研究实验介绍.物理实验,2017,37(3):25-36
16司丽荣,张竞夫.弹簧摆内共振现象的实验研究.物理实验,2001,22(3):9-12
17司丽荣,张竞夫.用摄像机和计算机记录物体的3维运动.物理实验,2002,22(9):38-40
18李炉锋,廖生海,孟宪嵩等.基于计算机视觉的机械运动分析.物理实验,2016,36(11):10-12
V216.2+2
A
10.6052/1000-0879-17-256
2017–07–19收到第1稿,2017–10–19 收到修改稿.
1)E-mail:fangh@hitwh.edu.cn
周成博,宋一诺,范光华.复合摆和耦合摆运动的可视化.力学与实践,2017,39(6):641-647
Zhou Chengbo,Song Yinuo,Fan Guanghua.Visualization of the vibration of compound pendulum and coupled pendulum.Mechanics in Engineering,2017,39(6):641-647
(责任编辑:周冬冬)
