基于周期延拓的步进式正弦扫频阻抗控制方法1)

张步云 汪若尘 孙晓东 曾发林

(江苏大学汽车工程研究院，江苏镇江212013)

基于周期延拓的步进式正弦扫频阻抗控制方法1)

张步云2)汪若尘 孙晓东 曾发林

(江苏大学汽车工程研究院，江苏镇江212013)

针对步进式多输入多输出正弦扫频振动试验中相邻信号过渡不平顺以及多点相位控制精度差的问题，分析扫频频率切换机理，在保证试验时间以及多点相位差满足参考容差要求情况下，提出周期延拓法平稳地处理两段不连续信号；提出了阻抗多点控制算法，分析了压缩因子对收敛速度与控制精度的影响，设定频响函数矩阵条件数阈值以避免结构病态频率带来的过激励影响；开展多轴多点正弦扫频振动算法试验，结果验证了算法可靠性与有效性.

环境试验,正弦扫频,信号处理,振动控制,步进式扫描

正弦扫频环境试验有连续扫频和步进式扫频两种方式[1].连续扫频的频率是时刻变化的，而步进式扫频的频率阶跃性变化，但整体呈现线性或对数变化的趋势.连续扫频主要用于模态分析，其频谱为连续谱.而步进式正弦扫频试验是寻找结构共振点、开展产品可靠性与耐久性研究的重要方法[23]，在振动环境试验中被广泛应用[48].由于发出的正弦信号频率不是连续的，且相邻频率段信号发送无时间间隔，所以两段信号连接处常发生跳跃现象[910].这种不平顺的连接使得激振器或振动台遭受到冲击，产生严重的冲击噪声.步进式多输入多输出(multiple input multiple output,MIMO)试验更符合机械产品、设备或零部件实际经历的工作振动环境，能有效避免单轴单向试验的欠试验或产生应力集中的问题.Smallwood[1113]和Underwood等[14]针对MIMO在多点正弦振动试验系统中的频响函数估计、驱动信号生成以及控制算法等多方面问题提出了系统的理论，并将其应用到工程实践中.但基于商业机密的考虑，国外振动控制设备的处理算法并不对外公开发表.我国虽在MIMO振动试验研究方面起步较晚，近年来国内学者在这一领域也开展了大量的研究.杨志东等[15]分析了正弦扫频信号相位函数的微分方特点，提出一种新的信号综合算法得到正弦驱动信号.于慧君等[16]提出了采用窗函数进行加窗重叠的处理方法，虽然试验结果证明该方法能较好地进行信号平滑连接，但加窗重叠方法缩短了原始信号的长度，不满足扫频时间要求.为此本课题组在前期大量研究前提下[1718]，提出加窗延拓法[19]，在保证信号平滑过渡的同时，还能保证振动时间满足试验标准要求.但其忽略了多点之间相位差的控制，且并未考虑由于过度修正引起的冲击效应.

综上所述，对于正弦扫频相邻不连续信号的搭接处理大多局限于幅值上的平滑过渡，对多点正弦扫频试验的相位控制并不理想.为了解决此问题，本文基于线性振动理论提出周期延拓法得到能够同时满足试验时间与相位差要求的连续信号.另一方面，考虑到正弦激励信号修正过程中过度激励问题，提出阻抗控制方法，使得正弦振动控制在满足收敛速度要求的同时保证控制精度.最后通过多轴振动实验验证了算法的可靠性.

1 MIMO正弦扫频试验控制系统

MIMO正弦扫频试验系统包含外载系统和控制系统，如图1所示.外载系统由功率放大器与振动台系统组成，控制系统主要功能是对采集到的振动信号进行分析处理，与参考值比较后修正激振信号并将其传递给外载系统，核心部分是振动控制算法.

根据产品不同的振动环境设定试验频带、扫描方式、时间和次数，同时必须设定整个频带上不同控制点处的幅值与相位.在试验过程中，外载系统不断将信号输送给控制系统，控制仪实时识别信号幅值与相位，并计算当前的扫描频率，通过算法修正激励信号，再将其传送给外载系统.如此循环，直至振动信号满足参考值要求.

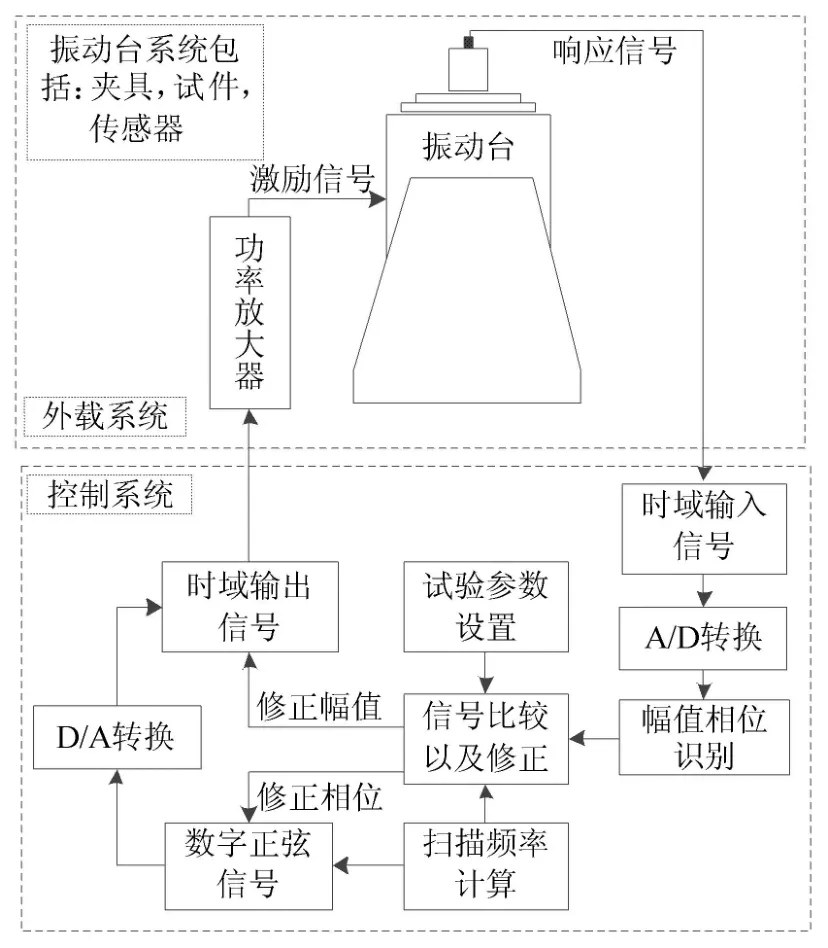
图1 正弦扫频试验系统

2 扫频信号不平顺连接问题

2.1 扫描率计算

由于低频正弦波测量比高频测量要消耗更多时间，且对数扫描更能反映大多数机械或电子系统的动态频域特征，所以本文仅针对对数扫描信号进行分析.设扫描的起始频率为fs，终止频率为fd，单次扫描时间为Ts，则对数扫描率β(oct/s)可计算为

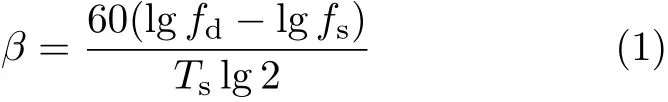
式中β表示对数扫描率.则可计算出在时刻tk时正弦频率fk为

2.2 相邻频段信号连接

步进式扫描频率不是连续的，设定好试验时间Ts后，根据试件结构频域特征，设置扫描最小的频率分辨率，得出扫描的频率点数n.每个频率点驻留时间为Δt=Ts/n，如图2所示.

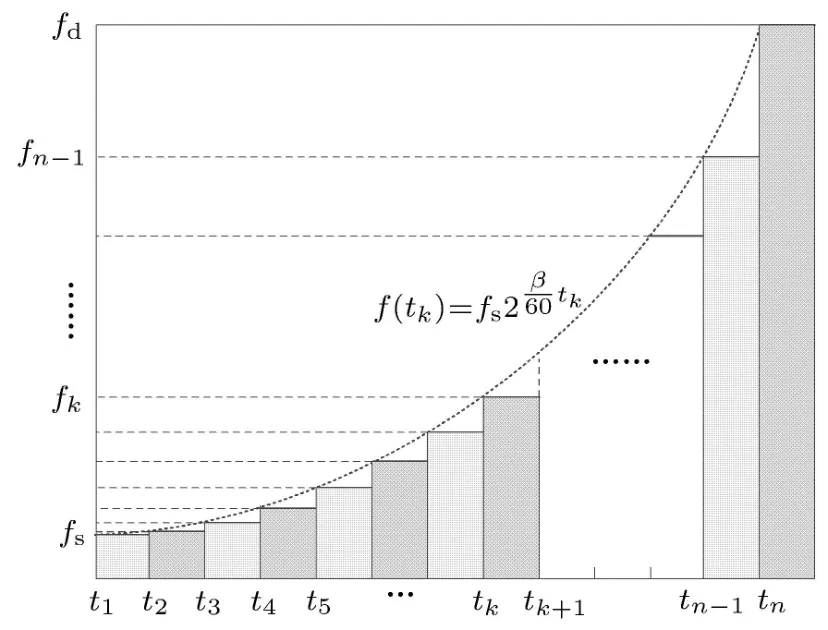
图2 扫描频率计算

根据线性振动理论，多点激励与响应在频域的关系为

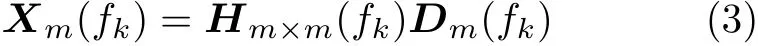
式中，m是控制点数，Xm(fk)={|xi(fk)|exp[ϕi(fk)]}(i=1,2,···,m)表示响应信号，含幅值与相位信息，Hm×m(fk)表示振动系统的频响函数矩阵，Dm(fk)={|di(fk)|exp[ψi(fk)]}(i=1,2,···,m) 表示激励信号.设定参考值 Rm(fk)作为系统的理论响应，测得频响函数后便可计算出理论激励信号为

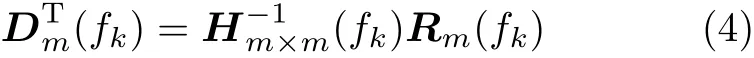
考虑到从低频到高频的频率切换过程中幅值与相位均不是连续变化的，前一段信号的末尾与后一段信号的起始值并不相同，这种幅值上的跳跃会造成振动设备产生冲击作用，这在振动试验中是不允许的.

2.3 平滑处理周期延拓法

设两段相邻的正弦信号频率为f1与f2，幅值为a1与 a2，相位为 ϕ1与 ϕ2，分别用 x1与 x2表示.

信号x1在((p−1)Δt,pΔt)时刻内，信号x2从pΔt时刻某开始，驻留在(pΔt,(p+1)Δt)时刻内，p=1,2,···,n−1.在幅值上，x1(pΔt)/=x2(pΔt)，如图3所示，实线表示x1，虚线表示x2.

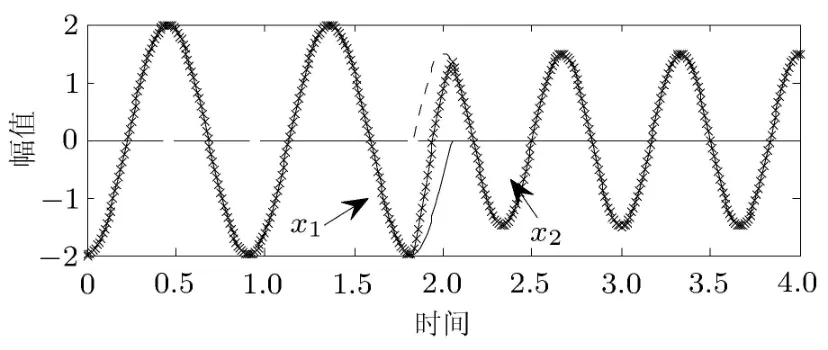
图3 周期延拓法示意图

为了使两段信号平滑过渡，且保证试验时间和相位差能够满足试验条件与参考值设定要求.将x1信号顺时延长至tp时刻，使x1(tp)=0，得到信号；同时将 x2信号逆时延长至 tp−1时刻，使得 x2(tp−1)=0，得到信号 x∗2. 此时

再将x∗1与x∗2相加得到新的信号x∗，如图3所示，带“×”实线为修正后的过渡信号.该信号平稳地连接前后两段信号，并且信号之间没有断层，也并未缩短信号的长度，同时保证了相位的正确性.

3 阻抗控制算法

3.1 算法推导

根据式(4)求出的信号是理论驱动信号，H 是结构真实的频响函数.而实际上通过模态试验得到的实测频响函数G与H 之间并不一致，它们之间有一定的误差，再通过式(4)计算出的驱动信号并不能使响应满足参考值的设定要求

从式中可以明显看出响应式不满足参考值要求.试验中频响函数是作为第一步测量的，其值固定不变，故通过修正激励信号来不断调整响应信号与参考值的容差性. 依据振动理论，系统阻抗矩阵为Z=G−1，可以计算出第一次激励为

在正弦振动试验中，有时响应的幅值与参考值之间误差较大，通过误差修正激励信号往往会使得幅值产生突变，这会对设备产生冲击以致损坏.故需引入压缩因子α∈(0,1)来缓冲这种突变，α的意义即为将误差的α倍作为“修正误差”带到控制算法中，以减缓激励信号的突变.另一方面，α的引入导致修正速度减慢，不过为了使控制更加稳定、控制精度更高，压缩因子设定显然有实际意义.

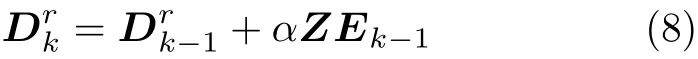
令HZ=I−ΔI，带入上式可得

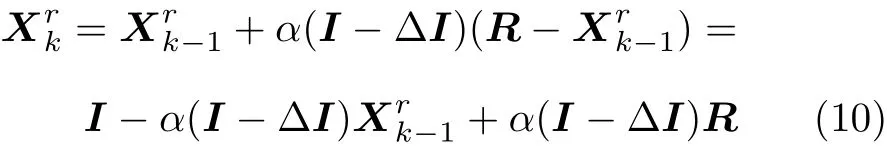
利用数学归纳法，第k−1次响应为

将式(11)带入式(10)，并依次推导得

因α∈(0,1)，有 1−α∈(0,1)，则当k趋于足够大时，I−α(I−ΔI)k−1=0，则式 (12)有

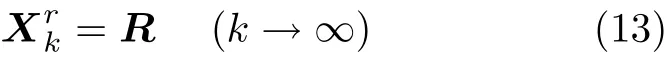
图4 压缩因子α对收敛速度的影响

式(8)即为阻抗控制算法，式(9)∼式(13)证明了其收敛性.图4显示了不同压缩因子对控制收敛速度的影响.当压缩因子趋近于0时，收敛速度较慢，需要多次迭代才能将响应控制在参考值10%之内；当压缩因子趋近于1时，收敛速度较快，但对设备造成冲击的弊端并未减少.综合考虑两者，一般取压缩因子α在0.3到0.5之间.

3.2 频响矩阵奇异值处理

由式(7)知阻抗控制算法中需要对频响函数进行求逆，注意到在实际结构振动中，频响函数矩阵往往在某个频率点上存在近似于奇异阵的病态情况，这将对其求逆产生严重的影响.为避免由此带来的激振力过大，采用矩阵条件数来衡量这种病态情况

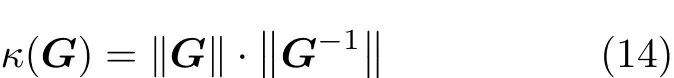
式中，‖·‖表示矩阵 G 的条件数.频响函数是正规矩阵，可用矩阵的最大奇异值和最小奇异值之比来表示

式中pinv(G)表示对矩阵G求广义逆.

4 试验验证

采用Shinken多轴振动试验台台面振动作为控制对象，以振动台面在X轴与Y轴的振动作为试验系统的控制目标，如图5所示.试验中以VXI系统作为数据采集与发送系统，EX2500A为数采系统控制中心，VT1432A为数据发送模块，VT1436为数据采集模块.

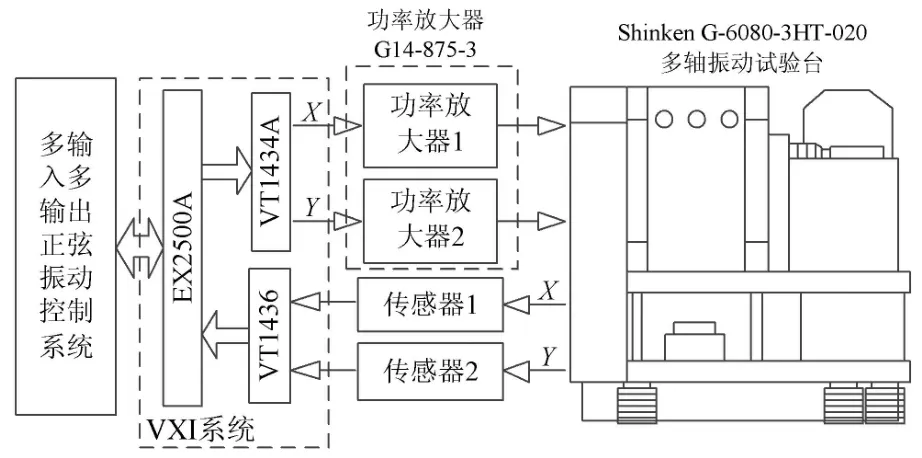
图5 MIMO正弦振动系统试验方案

数字信号数据通过VT1432A的D/A板转化为模拟信号通过功率放大器传送到振动台，振动台面的振动通过传感器拾取信号，再经过VT1436模块传送到控制系统进行处理.

试验针对振动台X轴和Y轴两个方向的振动进行控制，依据工程结构常用频率设定扫描频率为10∼2000Hz，上下限频率的设定可以验证本文算法在高低频试验控制中均是有效且可靠的.扫描方式为对数扫描，单次扫描时间为5分钟，驻留频率点数为200个，通过计算出扫描率为1.54oct/min.两轴向振动参考值设定如表1所示.

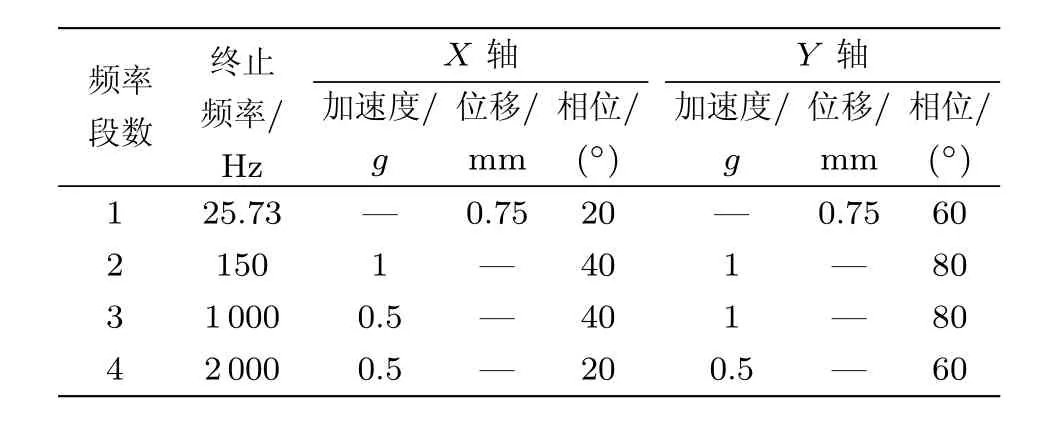
表1 X 轴与Y轴振动参考值设定

正弦控制试验是实时控制，为说明本文控制算法有效，分别对未控制试验结果和控制后的结果进行对比，试验现场如图6所示.

图6 试验现场

图7∼图9分别是未控制时X轴、Y轴以及相位差响应结果.图中最上与最下两条实线表示参考值的±20%，为试验停止线，中间两条虚线表示参考值的±10%，为试验警报线.中心点划线为参考值，围绕其上下波动的实线为实际测得振动响应的幅值与相位.

图中上下两条实线表示的是中止容差带，两条虚线表示的是警报容差带，中心点划线表示参考值,实际响应围绕参考值上下波动.从图中可以看出在未进行控制前，无论幅值还是相位与参考值均有较大的误差.X轴在84Hz和363Hz两频率初的幅值响应均超出参考值的警报线，Y轴在96Hz初的幅值也有超标现象存在，而其他频带上均有程度不一的超标.在两轴的相位差结果中，1000Hz以下的响应大多在参考值容差带之内，但在1705Hz处的相位远低于参考值.本试验中压缩因子选择0.4，经过5次均衡之后，控制结果如图10∼图12所示.

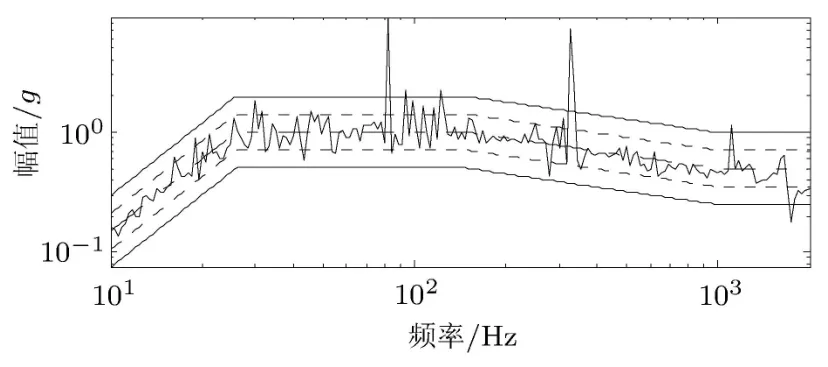
图7 X轴未控制时两轴相位差响应结果

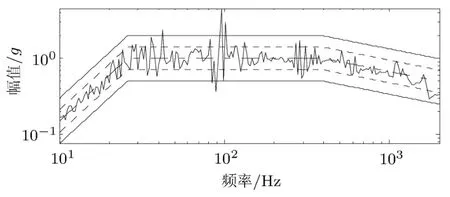
图8 Y轴未控制时幅值响应结果

图9 Y轴未控制时两轴相位差响应结果

图10 X轴控制后幅值响应结果

从控制结果来看，X轴在84Hz以及363Hz处的响应由超标 8∼9倍控制到 10% 以内，Y 轴在95Hz处的响应幅值也由超标两倍降低到 10%之内，两控制点之间1705Hz处的相位差由−8°控制到40°的容差范围内.此外，全频域的幅值均能够控制到参考值的容差带之内.控制结果显示无论是在幅值还是相位上，本文的控制算法可靠，且控制精度高，达到了振动试验的工程标准.

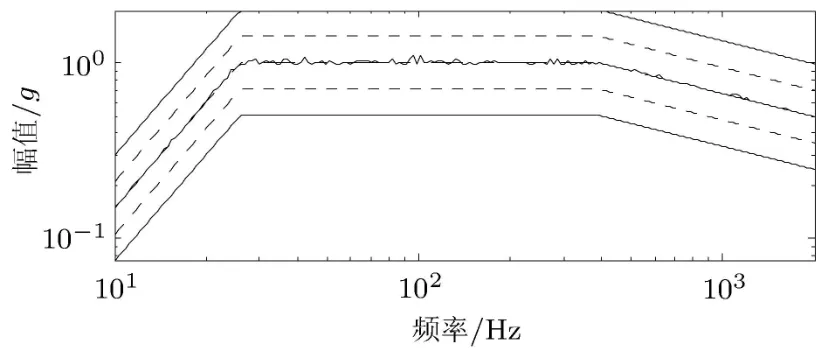
图11 Y轴控制后幅值响应结果

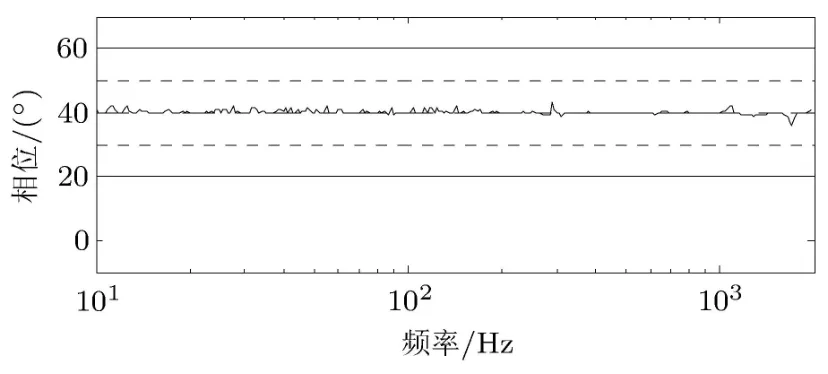
图12 控制后两轴相位差响应结果

5 结论

(1)深入分析了多点激励信号生成过程中前后两段相邻信号在首尾连接处的不平顺问题产生的机理，考虑振动试验时间与相位差两者共同要求，提出了周期延拓平滑处理方法，将信号通过顺、逆时序延拓至零点求和，保证正弦激励信号在频率切换过程中平稳过度，使得振动设备避免因冲击而损坏；

(2)提出了阻抗控制算法，通过引入压缩因子缓解了激励信号过度修正问题，分析了压缩因子对于结果修正精度与速度的影响，基于线性振动理论详细推导了控制算法的修正公式，并利用数学归纳法证明了算法的收敛性.

(3)开展多点正弦试验研究，通过设定频响函数矩阵的条件数阈值判定结构的病态频率，控制结果说明本文提出的算法能同时控制多点正弦幅值与相位，控制精度能够满足工程需要，表明算法具有重要的理论意义与使用价值.

1 MIL-STD-810G.Environmental engineering considerations and laboratory tests.2008

2 Zhao XY,Kai PY.Finite element model updating of damped structures using vibration test data under base excitation.Journal of Sound and Vibration,2015,340:303-316

3 Mahdi K,Amir H,Hans KH,et al.Study on locating transformer internal faults using sweep frequency response analysis.Electric Power Systems Research,2017,145:55-62

4 Cveticanin L.Period of vibration of axially vibrating truly nonlinear rod.Journal of Sound and Vibration,2016,374:199-210

5 Paulo AD,Daniel MS,Roque AO,et al.Methodology for fault detection in induction motors via sound and vibration signals.Mechanical Systems and Signal Processing,2017,83:568-589

6王猛,郑梅生,田连军等.用振动试验方法测定羽毛球拍杆的刚度.力学与实践,2013,35(1):69-71

7 Claeys M,Sinou JJ,Lambelin JP,et al.Modal interactions due to friction in the nonlinear vibration response of the“Harmony” test structure:Experiments and simulations.Journal of Sound and Vibration,2016,376:131-148

8 Hoffait S,Marin F,Simon D.Measured-based shaker model to virtually simulate vibration sine test.Case Studies in Mechanical Systems and Signal Processing,2016,4:1-7

9 Amir S,Joseph M,Yves G.Damage monitoring in sandwich beams by modal parameter shifts:A comparative study of burst random and sine dwell vibration testing.Journal of Sound and Vibration,2010,329(5):566-584

10 Claeys M,Sinou JJ,Lambelin JP,et al.Experiments and numerical simulations of nonlinear vibration responses of an assembly with friction joints–Application on a test structure named “Harmony”.Mechanical Systems and Signal Processing,2016,70-71:1097-1116

11 Smallwood DO.Multiple input multiple output(MIMO)linear systems inputs/outputs.Shock and Vibration,2007,14(2):107-131

12 Smallwood DO.Using a modified harmonic wavelet transform to characterize mechanical shock.Journal of IEST,2011,54(2):85-102

13 Smallwood DO.Minimum input trace for multiple input multiple output linear systems.Journal of IEST,2013,56(2):57-67

14 Underwood MA,Keller T.Testing civil structures using multiple shaker excitation techniques.Journal of Sound and Vibration,2008,42(4):10-15

15杨志东,丛大成,韩俊伟等.正弦扫频振动控制中的信号综合与信号分析.振动工程学报,2008,21(3):309-313

16于慧君,陈章位,王庆丰.一种加窗重叠信号平滑连接方法及其在振动信号预处理中的应用.振动与冲击,2007,26(8):39-40

17贺旭东,陈怀海,申凡等.多点简谐振动响应控制下的频响函数矩阵测试.航空学报,2006,27(5):869-872

18朱银龙,陈怀海,贺旭东等.多输入多输出正弦振动试验控制系统算法研究及实现.振动工程学报,2008,21(1):62-65

19张步云,陈怀海,贺旭东.多输入多输出正弦扫频试验控制新方法.振动与冲击,2015,34(8):198-202

IMPEDANCE CONTROL METHOD OF STEPPED SWEPT SINE VIBRATION TEST BASED ON PERIODIC EXTENSION1)

ZHANG Buyun2)WANG Ruochen SUN Xiaodong ZENG Falin
(Jiangsu University Automotive Engineering Research Institute,Zhenjiang 212013,Jiangsu,China)

The discontinuity between two adjacent sine signals and the poor control precision are two difficult problems in the multiple input multiple output(MIMO)swept sine vibration test.This paper proposes a new method to smooth the discontinuous signal segments of sinusoid waves at different frequencies,to guarantee the test time requirement and the phase tolerance requirement of the reference.The compression impedance control method(CICM)is proposed to solve the over correction problem of the excited signals.The impacts on the rate of convergence and the control precision are analyzed,and the threshold of the frequency response function matrix(FRFM)is set to avoid the over excitation of the singular FRFM at some special frequencies.Finally the paper establishes the test conditions for the multiple axis vibration test,and tests the algorithm for the multiple axis swept sine test.It is shown that the amplitude and phase responses could be controlled within the tolerance range of the reference values by the 5 times correction,when the compression factor value is 0.4,and the control algorithm is shown to be reliable.

environmental test,swept sine,signal processing,vibration control,stepped scanning

O328

A

10.6052/1000-0879-17-105

2017–03–27收到第1稿，2017–05–03 收到修改稿.

1)国家自然科学基金(51705205),江苏省高校自然科学研究面上项目(16KJD460001)和江苏大学高级人才科研启动基金(15JDG166)资助.

2)张步云，讲师，主要研究方向为振动测试与控制.E-mail：zhangby@ujs.edu.cn

张步云,汪若尘,孙晓东等.基于周期延拓的步进式正弦扫频阻抗控制方法.力学与实践,2017,39(6):573-578

Zhang Buyun,Wang Ruochen,Sun Xiaodong,et al.Impedance control method of stepped swept sine vibration test based on periodic extension.Mechanics in Engineering,2017,39(6):573-578

(责任编辑:周冬冬)