基于修正模态应变能指标的板结构损伤定位1)
2018-01-06梁振彬张华昕
梁振彬 董 聪 张华昕
(清华大学土木工程系,北京100084)
基于修正模态应变能指标的板结构损伤定位1)
梁振彬2)董 聪 张华昕
(清华大学土木工程系,北京100084)
为解决模态应变能方法识别中产生的“邻近效应”问题,提出基于修正模态应变能指标的板结构损伤定位方法.该方法首先利用邻近测点的应变能变化相对大小计算权重系数,再根据权重系数对测点相应区域的应变能进行重新分配.此外,通过定义的损伤辨识度指标研究噪声对损伤定位结果的影响.为验证本文所提方法的可行性和有效性,以一个四边简支板为数值算例.算例结果表明,本文方法对于点状、块状和带状损伤都可以实现准确定位,且具有良好的抗噪性.
损伤定位,板结构,模态应变能,抗噪性
在土木工程领域,板作为一种重要的构件被广泛使用. 板的损伤识别研究通常包括损伤是否存在、损伤定位以及损伤程度识别3个阶段.其中板的损伤定位是至关重要的一个阶段,是后续损伤程度识别的基础.基于损伤前后的振动特性来进行损伤定位是常见的方法,如频率变化[1]、振型变化[23]、模态曲率变化[4]和模态应变能变化[57]等.诸多研究表明[810],相比于频率和振型,模态曲率和模态应变能对板的损伤更加敏感.
Shi等[56]通过提出的单元模态应变能改变率指标对结构损伤进行定位.Cornwell等[7]使用二维曲率将模态应变能方法拓展到了二维板结构中.Hu等[11]在 Cornwell研究的基础上,定义一个扫描区域,利用数值积分方法计算模态应变能中的偏微分项,并将其应用于板的表面裂缝损伤定位.Fan等[12]利用模态应变能构造损伤定位参数,并通过选取模态特征值改变率较大的敏感模态来提高损伤定位效果.Fu等[13]针对模态应变能方法定位结果中损伤单元邻近的模态应变能指标值相对较大的问题(也称为“邻近效应”),通过邻近单元的模态应变能值和权重系数来修正原指标,并对比分析了不同权重系数的修正效果.Wei等[14]则通过改进的二分法进行迭代来确定权重系数,从而优化损伤定位结果.
在板结构的损伤定位过程中,为减弱模态应变能方法中“邻近效应”的影响,本文首先利用损伤前后的模态应变能差值构造损伤指标,之后通过邻近单元与中心单元的模态应变能差值之比计算权重系数,对构造的损伤指标进行修正.并以四边简支薄板为研究对象,对点状、块状和带状三种类型损伤的定位效果进行研究.此外,还研究了测量噪声对损伤定位结果的影响.
1 理论背景
1.1 板的模态应变能指标
板的损伤模拟方法通常有两种:折减单元刚度和折减单元截面积.前者应用于板发生裂缝类损伤时较为合理,此类损伤未引起结构质量发生改变.本文中假定板发生的都是裂缝类的损伤,采用折减单元刚度来模拟结构损伤.
弹性板的模态应变能为[7]
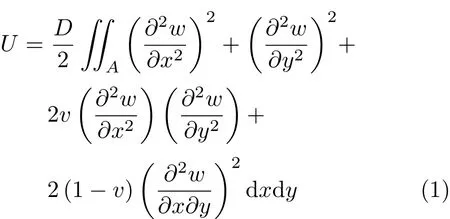
式中,U为板的模态应变能,A为矩形板的面积,D=Eh3/[12(1−v2)]为板的抗弯刚度,ν为材料泊松比,h为板厚,w为板的横向位移为板的弯曲曲率为板的扭转曲率.
为表述方便,上式中的曲率记为
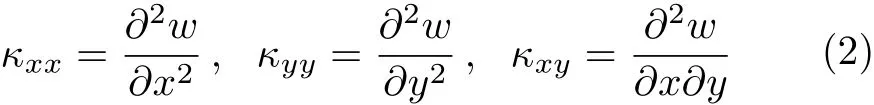
对于第i阶振型φi,板结构总的模态应变能为
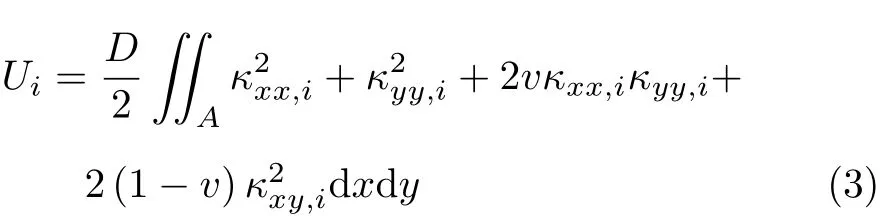
将矩形板划分成 Nx×Ny个单元,如图 1所示.定义板单元 (j,k)的区域为 Ejk={[xj,xj+1],[yk,yk+1]}.则该单元第i阶单元模态应变能为
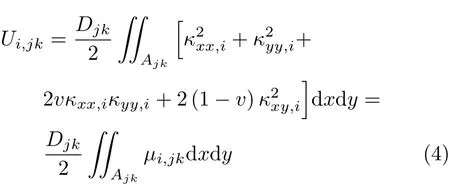
式中 Djk为板单元 (j,k)的抗弯刚度,Djk=D;Ajk为板单元面积.类似地,可以定义损伤时板结构的单元模态应变能为
以结构损伤前后的单元模态应变能差定义损伤指标
对式 (6)中积分项内曲率的计算,常用的有两种方法:一是通过横向位移的差分来近似计算,二是直接通过应变计测量应变,由应变直接计算曲率.由于差分会引入新的误差,因此本文采用后一种方法计算曲率.对于满足Kirchhoff假定[15]的薄板,应变--曲率关系由下式给出
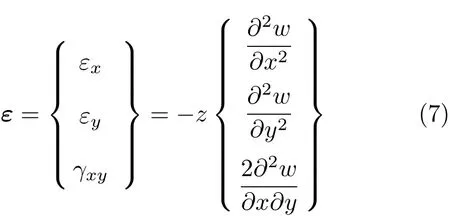
式中z为板表面到中性面的距离,即z=2/h.
1.2 损伤指标修正
由式 (6)知,对测点进行样条插值后即可计算某单元的模态应变能变化量指标 UI.结构损伤带有局部性质,这种全局插值方式会弱化损伤带来的局部变化,产生所谓的“邻近效应”[13].为减弱这种“邻近效应”的影响,通过邻近点的应变能变化相对大小定义权重.下面以板单元 (j,k)第 i阶振型为例,阐述损伤指标UI的修正方法.
对于点Pj,k=(xj,yk),定义其待分配的模态应变能区域为
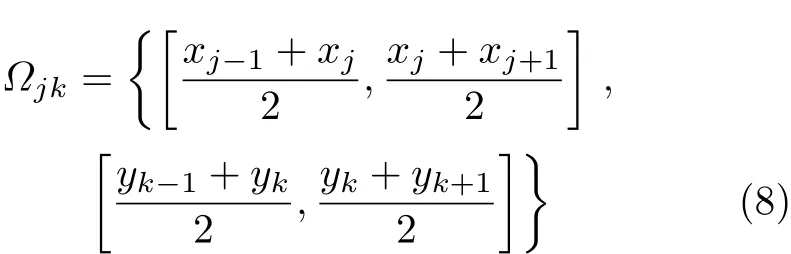
如图1中阴影部分所示.定义点Pj,k邻近的8个点Pm,n的Δµmn值与点Pj,k的Δµjk值之比为

式中m=j−1,j,j+1;n=k−1,k,k+1.与点Pj,k相邻的四个单元所对应的权重指标由下式计算
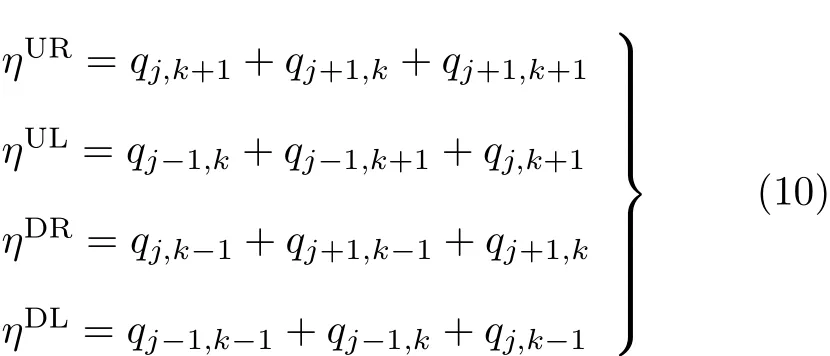
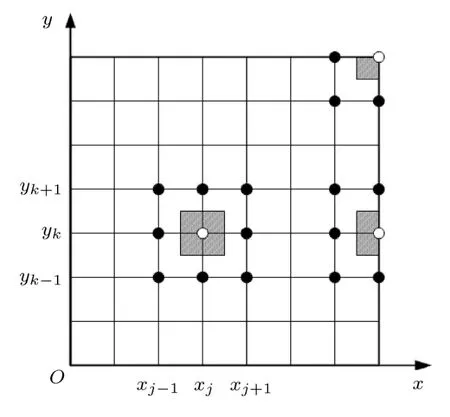
图1 板结构划分示意图
记 η= ηUR+ηUL+ηDR+ηDL,上标 UR,UL,DR,DL分别表示右上,左上,右下,左下的单元.利用权重指标对区域Ωjk中的模态应变能进行分配,与点Pj,k相邻的四个单元分配到的应变能为
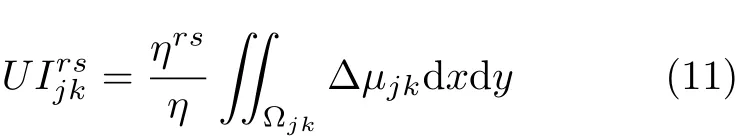
式中rs=UR,UL,DR,DL,分别代表右上,左上,右下,左下四个部分.
对于单元(j,k),利用式(11)将单元四个节点分配到单元(j,k)中的应变能值求和,即可得到新的单元模态应变能变化值,重新分配后的损伤指标MDI由下式计算
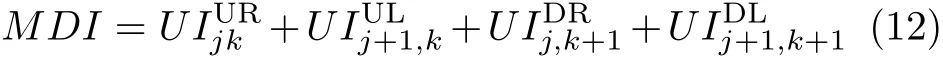
取前m阶振型进行计算,则单元(j,k)前m阶指标MDI

单元(j,k)的损伤指标MDI通过下式进行标准化
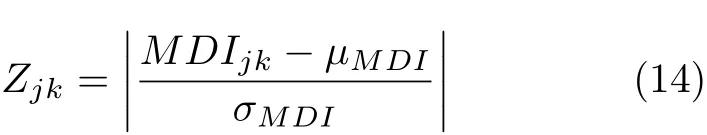
式中 βjk和 σjk分别代表损伤指标 MDI的均值和标准差.依据文献[7]中采用95%置信水平的损伤阀值,即将指标MDI大于2的单元视为损伤单元.
1.3 测量噪声
实际测试过程中噪声的影响不可避免.因此,有必要研究本文所提方法的抗噪性能.对应变模态施加噪声的公式为[9]

2 算例分析
以四边简支的弹性薄板为典型算例,验证本文所提方法的有效性.矩形板沿x方向的长度为5m,沿 y方向的宽度为 4m,板厚度为 0.04m.弹性模量为 E=70GPa,泊松比为 ν=0.3,材料密度为ρ=2700kg/m3.将板划分成 20×16个单元,每个单元长度为0.25m.板的有限元模型和3种损伤工况及其对应的损伤单元如图2所示.工况1为点状损伤,损伤工况2为块状损伤,损伤工况3为带状损伤.以折减单元刚度来模拟结构损伤,3种损伤工况中单元刚度折减量均为 30%,使用损伤前后前 5阶模态进行计算.
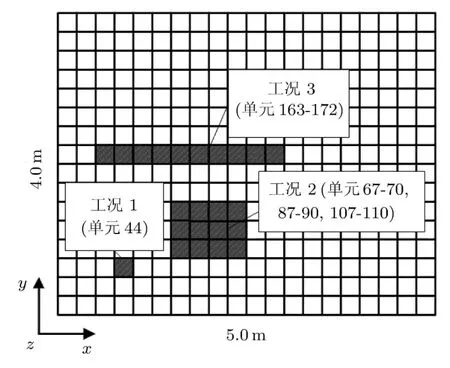
图2 板的有限元模型及损伤工况分布图

图3 工况1点状损伤识别结果

图4 工况2块状损伤识别结果
2.1 损伤定位结果
将本文损伤指标MDI定位结果与文献[7]的DI指标和文献[9]的DSCF指标进行比较,图3∼图5分别为3种工况下各指标识别结果的柱状图和损伤单元分布图.由图可知,DI,DSCF和 MDI三种指标均可以定位点状、块状和带状的损伤.三种指标中MDI指标识别出的损伤单元分布最接近真实损伤情况,其次是DSCF指标,DI指标虽然也识别出了损伤位置,但损伤位置附近处的值相对较大.对此,在单点损伤工况1中,通过对比图3中DI,DSCF和MDI三种指标的柱状图可以发现,相比于其他两种指标,MDI指标损伤单元处的值远大于邻近单元的MDI指标值,说明MDI指标可以有效减弱“邻近效应”的影响,减少疑似损伤单元个数,识别结果更加精确.

图5 工况3带状损伤识别结果
2.2 噪声对定位结果的影响
首先定义损伤辨识度指标

式中SAct为损伤位置处的损伤因子峰值;SRes为除去损伤位置外其他位置的损伤因子最大峰值.
以工况1单损伤为例,依据辨识度指标λ的结果研究本文方法的抗噪性能.定义单元44的损伤程度由小到大依次为 0.1,0.2,···,0.6.施加的噪声水平由低到高为2%,4%,···,10%.每种情况重复实验50次.噪声水平为x轴,损伤程度为y轴,图6和图7中分别以辨识度指标λ和未成功识别损伤位置的次数为z轴.

图6 辨识度指标柱状图
由图 6可以发现,损伤指标辨识度随着损伤程度的减小和噪声水平的增大而变差.无噪声条件下,任何程度的损伤均可准确识别.4%噪声水平下,MDI指标可以对 20%以上的损伤进行准确定位(λ>1).而在最极端的情况下,即 10%的噪声水平下损伤程度为10%时,损伤单元的辨识度指标λ值仅为 0.43.此时结构损伤结果被噪声淹没,无法进行损伤定位.

图7 未成功识别损伤位置次数
图 7显示了不同的噪声水平和损伤程度情况下,每种情况50次实验中未能定位到损伤位置的次数.由图可知,在损伤程度较大或噪声水平较低,即噪声水平与损伤程度之比小于0.4时,MDI指标均可以成功的识别到损伤位置(识别成功率大于95%).
3 结语
本文提出了基于修正损伤因子的板结构损伤定位方法.主要结论如下:
(1)本文所提的损伤定位指标MDI在点状、块状和带状三种类型的损伤工况下均可以准确指示出损伤位置.
(2)MDI指标可以有效地减弱模态应变能方法中的“邻近效应”,减少疑似损伤单元个数,识别结果更加精确.
(3)MDI指标具有良好的抗噪性能.对于损伤程度在30%及以上的情况,在噪声水平不大于10%的情况下均可实现准确定位. 对于损伤程度小于20%的情况,在噪声水平较低时也可识别出损伤位置.
1 Cawley P,Adams RD.The location of defects in structures from measurements of natural frequencies.Journal of Strain Analysis,1979,14(2):49-57
2梁远森,李国强.利用模态参数进行弹性薄板的损伤识别.振动与冲击,2004,23(3):91-94
3 Santos JVAD,Soares CMM,Soares CAM,et al.Development of a numerical model for the damage identification on composite plate structures.Composite Structures,2000,48(1-3):59-65
4 Goldfeld Y.Curvature rate approach to the evaluation of the stiffness distribution in plate-like structures.Journal of Sound and Vibration,2014,333(19):4483-4498
5 Shi ZY,Law SS,Zhang LM.Structural damage detection from modal strain energy change.Journal of Engineering Mechanics,2000,126(12):1216-1223
6 Shi ZY,Law SS,Zhang LM.Improved damage quantifi cation from elemental modal strain energy change.Journal of Engineering Mechanics,2002,128(5):521-529
7 Cornwell PJ,Doebling SW,Farrar CR.Application of the strain energy damage detection method to plate-like structure.Journal of Sound and Vibration,1999,224(2):359-374
8 Shih HW,Thambiratnam DP,Chan THT.Vibration based structural damage detection in flexural members using multi-criteria approach.Journal of Sound and Vibration,2009,323(3-5):645-661
9 Fan W,Qiao PZ.Vibration-based damage identification methods:a review and comparative study. Structural Health Monitoring,2010,9(3):83-111
10 Wang ZX,Qiao PZ,Xu JF.Vibration analysis of laminated composite plates with damage using the perturbation method.Composites Part B Engineering,2015,72:160-174
11 Hu HW,Wu CB.Development of scanning damage index for the damage detection of plate structures using modal strain energy method.Mechanical Systems and Signal Processing,2009,23(2):274-287
12 Fan W,Qiao PZ.A strain energy-based damage severity correction factor method for damage identification in platetype structures.Mechanical Systems and Signal Processing,2012,28(2):660-678
13 Fu YZ,Liu JK,Wei ZT,et al.A two-step approach for damage identification in plates.Journal of Vibration and Control,2016,22(13):3018-3031
14 Wei ZT,Liu JK,Lu ZR.Damage identification in plates based on the ratio of modal strain energy change and sensitivity analysis.Inverse Problems in Science and Engineering,2016,24(2):265-283
15张延庆.结构分析有限元法.北京:科学出版社,2016
THE DAMAGE LOCALIZATION FOR PLATE STRUCTURES BASED ON MODIFIED MODAL STRAIN ENERGY INDEX1)
LIANG Zhenbin2)DONG Cong ZHANG Huaxin
(Department of Civil Engineering,Tsinghua University,Beijing 100084,China)
In order to deal with the “vicinity effect” in the damage localization of plate structures,this paper proposes a method based on the modified modal strain energy.Firstly,the relative strain change at adjacent points are used to calculate the weight coefficients,Then the strain energy in the corresponding area is redistributed according to the weight coefficients.By defining a damage differentiation degrees index,the influences of the noise on the damage localization can be evaluated.To verify the feasibility and the effectiveness of the proposed method,a four edge simply supported plate is used as a numerical example.It is shown that the proposed method can realize an accurate damage localization in dot,block and strip damage cases,with a good anti-noise capability.
damage localization,plate structures,modal strain energy,anti-noise capability
TU311.3
A
10.6052/1000-0879-17-108
2017–03–29收到第1稿,2017–06–25 收到修改稿.
1)国家电网公司科技项目(GC71-12-001)资助.
2)梁振彬,硕士研究生,主要从事结构损伤识别研究.E-mail:liangzhenbin1992@163.com
梁振彬,董聪,张华昕.基于修正模态应变能指标的板结构损伤定位.力学与实践,2017,39(6):585-590
Liang Zhenbin,Dong Cong,Zhang Huaxin.The damage localization for plate structures based on modified modal strain energy index.Mechanics in Engineering,2017,39(6):585-590
(责任编辑:胡 漫)
