侵彻试验尺度效应和相似准则1)

蒋 东 黄瑞源 余道建 周 刚 ,3)

∗(北京航天长征飞行器研究所,北京100076)

†(中国科学技术大学近代力学系，合肥230026)

∗∗(西北核技术研究所，西安 710000)

侵彻试验尺度效应和相似准则1)

蒋 东∗,†,2)黄瑞源†余道建∗周 刚∗∗,3)

∗(北京航天长征飞行器研究所,北京100076)

†(中国科学技术大学近代力学系，合肥230026)

∗∗(西北核技术研究所，西安 710000)

利用球形空腔膨胀理论的响应函数对靶板在弹体撞击下的侵彻进行分析，并基于量纲理论建立了侵彻相似律的一般形式.通过对侵彻混凝土靶的已有实验数据进行分析，得到了不同缩比因子下，无量纲侵彻深度曲线随侵彻速度不同而发生偏转和偏移.考虑到材料的应变率效应和损伤演化，认为几何相似律对混凝土等脆性材料在抗侵彻时不成立，有必要引入材料应变率效应和损伤演化对几何相似律的修正.

侵彻，相似律，缩比

尺度效应在许多工程问题如航空航天、武器等方面有着重要的应用，所以研究尺度效应有着特别的现实意义.尺度效应一直是研究的难点，也已经成为近十年来人们研究的热点之一，目前国内外许多学者对尺度效应进行了大量理论和实验研究[15]，所谓“尺度效应”是指，在一个现象里面，所讨论的宏观尺寸会与其他力学或物理特征量耦合成为一个无量纲控制参量，或者说，讨论的对象不再服从几何相似律，从而，室内小型实验结果，不能简单地推广到工程原型中去[6].

高速撞击的尺度效应作为一个特殊的研究领域，涉及高压、高速、高温等极端条件，涉及流体、固体等多个形态，同时又涉及物理、化学、材料科学相结合的特点，又要同时处理材料尺度和结构尺度相结合的复杂问题，对于这些复杂的问题，必须要通过理论结合实验的方法进行研究.在高速撞击实验领域，由于高速条件下很难将大质量的物体加载到高速，通常试验为缩比试验，不过高速撞击缩比试验某些参数在理论上是相似的，考虑到实验室条件的加载方式和能力，通过量纲理论结合缩比实验比对相关参数，建立一般的规律性，有助于深入理解所研究问题的本质，找到不同尺度问题的相似性，并作出定性分析.

1 弹丸的侵彻方程和材料本构不含时效的几何相似律

以锥头弹为例，图1给出了锥头弹丸的几何尺寸：弹体半径为 a，直径为 d，弹全长为L，弹头部长度为Ln，锥顶角为2β.

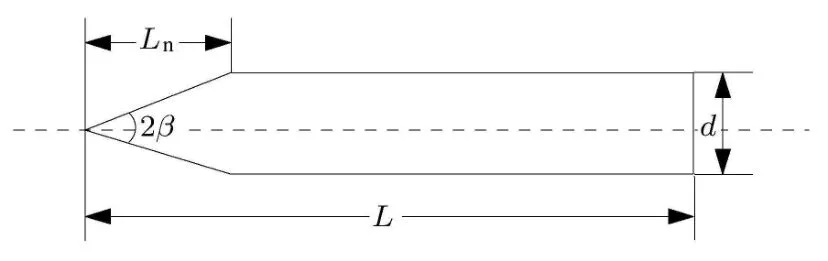
图1 锥头弹示意图

假设弹体垂直侵彻半无限靶板，侵彻深度为D，弹体的初始撞击速度为 v0，弹体在运动方向上的位移为W.则对于锥头弹丸[78]，侵彻可分为两种情况：(a)D≤Ln和(b)D＞Ln.以下对这两种情况分别进行分析.

假设弹体为刚体，侵彻过程中若弹体没有明显的塑性变形，该假设成立.开坑阶段(D≤Ln)时，弹头没有完全进入靶板，可得到弹体在侵彻方向所受阻力(含摩擦力)为

σn为靶板响应函数，µ为滑动摩擦系数.

完全侵入(D＞Ln)时弹体头部最终完全进入靶板.当弹体头部完全进入靶板之后，弹体在侵彻方向所受阻力为

式中，A0=πa2为弹体截面面积.式 (2)中，仍没有确定的物理量为靶板响应函数σn，可采用球形空腔膨胀理论研究靶板的响应函数.基于Forrestal半经验公式的靶板响应力函数适用于混凝土和岩石材料，若弹体为刚体，文献[9-11]给出的锥形弹开坑区和完全侵入区作用在弹头头部的轴向阻力为

其中，c为待定常数，˙W为刚体弹侵彻过程中的瞬时速度，S是相关于混凝土无围压压缩强度fc的一个无量纲经验常数，有

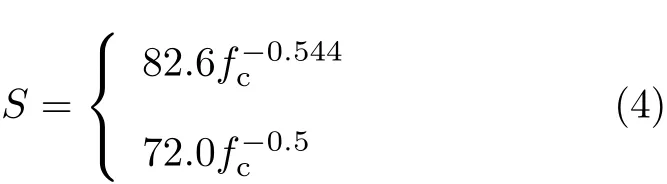
式中，fc的单位为MPa.

此外，文献[7]基于能量守恒认为，弹体侵彻过程中受到的靶板造成的表面法向平均压力可以分为两部分：一是由靶板材料的弹塑性变形引起的静阻力σs;二是由速度效应引起的动阻力σd.因此有

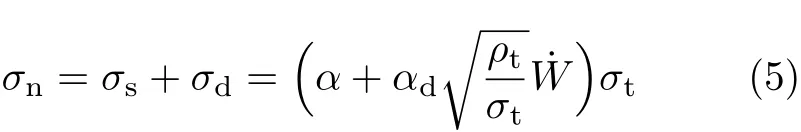
无论是基于空腔碰撞理论的Forrestal半经验公式，还是基于能量守恒的半经验型响应函数，都认为弹体的侵彻深度与弹靶材料力学特性，弹体着靶速度，弹体质量、直径、头部形状，弹体与靶板之间的摩擦系数等有关，与其他量无关.

当给定弹、靶材料时，或者说给定材料特性，包括代表惯性的密度ρp,ρt，代表弹靶破碎特性的破碎强度Yp,Rt；给定弹的几何形状和特征尺寸L，以及弹体速度大小˙W，根据量纲理论，显然有侵彻深度

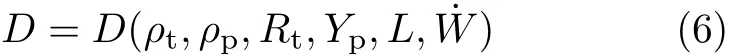
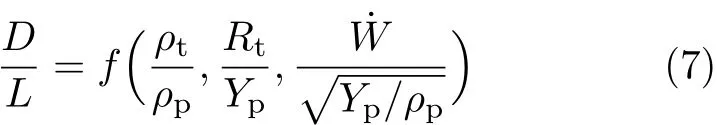
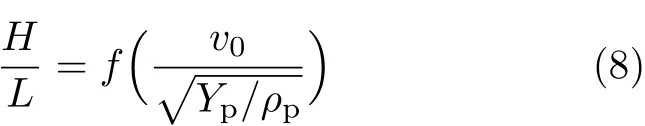
这便是在确定弹形 (几何相似)和确定弹靶材料组合下的高速侵彻相似律，由此可得出一个重要的结论：

我们采用的模型和原型具有相同的弹、靶材料和几何相似的弹体结构形状，并且具有相同的弹速v0，则由式(8)可以看出和一定相同，其中 y和 m各表示原型和缩比模型.假设缩比因子为ξ，缩比弹长为Lm，原型弹长为Ly，缩比模型与原型的几何尺寸的缩尺比为，则几何尺寸和缩比因子成比例：Ly=ξLm；应变是相同的：ε=E；应力是相同的：σ=P；静水压是相同的：p=P；材料中的声速是相同的：c=C；时间与缩比因子成比例：T=ξt；速度是相同的：v=V.

2 材料本构包含时效的几何相似律

上述结论忽略了材料响应的时效，材料本构中与时间相关项是不符合几何相似律的，一种是材料的应变率敏感性.当材料响应的应变率效应不明显而可以忽略时，侵彻几何相似律基本是成立的.对于金属靶板，如果应变率效应不太明显，从实验和数值计算结果来看其几何相似律是基本成立的.对于混凝土侵彻，一般认为，由于混凝土是一种应变率较敏感的材料，只有缩比因子较小时，才基本满足几何相似律，当缩比因子较大时，其工程实际实验值与几何相似模型值由于应变率相差较大从而呈现较大的偏离.侵彻过程中，应变率在侵彻过程中随着弹速一直变化，但应变率是速度与弹的尺寸的函数，因为缩比小尺度的试验应变率大于原型实验.

二是材料的损伤演化.文献[12]认为，材料的动态拉伸破坏和绝热剪切破坏是时率相关的，文献中提出的修正的Tuler--Butcher模型认为，某一时刻的损伤一定会影响下一时刻的损伤演化，由于时间是与缩比因子成比例的，从而动态拉伸破坏是不符合缩比律的；绝热剪切破坏准则包括材料动态再结晶的应变率效应，此外绝热剪切时损伤演化、热传导效应也与时间相关，所以绝热剪切破坏也是不符合相似律的.

表1∼表 3给出了描述混凝土的侵彻试验数据，表 1中缩比因子为2，原型弹质量(460±2)g，弹体直径 20mm，靶板 fc为 16.5MPa；缩比弹质量 58g，弹体直径 10mm，靶板 fc为 16.5MPa，其中 2号缩比弹质量为 56.5g，与其他弹体质量不一致，拟合曲线时将该数据去除.两种弹的CRH值(弹头轮廓母线的曲率半径和弹径之比)均为 3；侵彻速度范围为206∼657m/s，混凝土靶板抗压强度为16.5MPa.

表2中缩比因子也为2，但原型弹质量较大，为46kg，直径 152mm，靶板 fc为 30MPa；缩比弹质量6.275kg，直径75mm，靶板fc为30MPa；两种弹的CRH值均为4.侵彻速度范围为450∼650m/s，混凝土靶板抗压强度为30MPa.

表1 文献 [13]侵彻实验数据

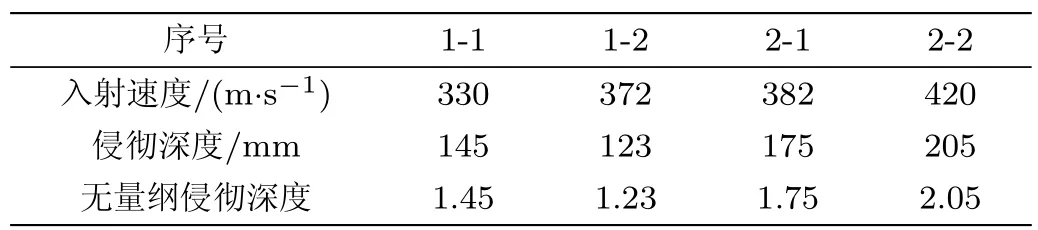
表2 文献 [14]侵彻实验数据

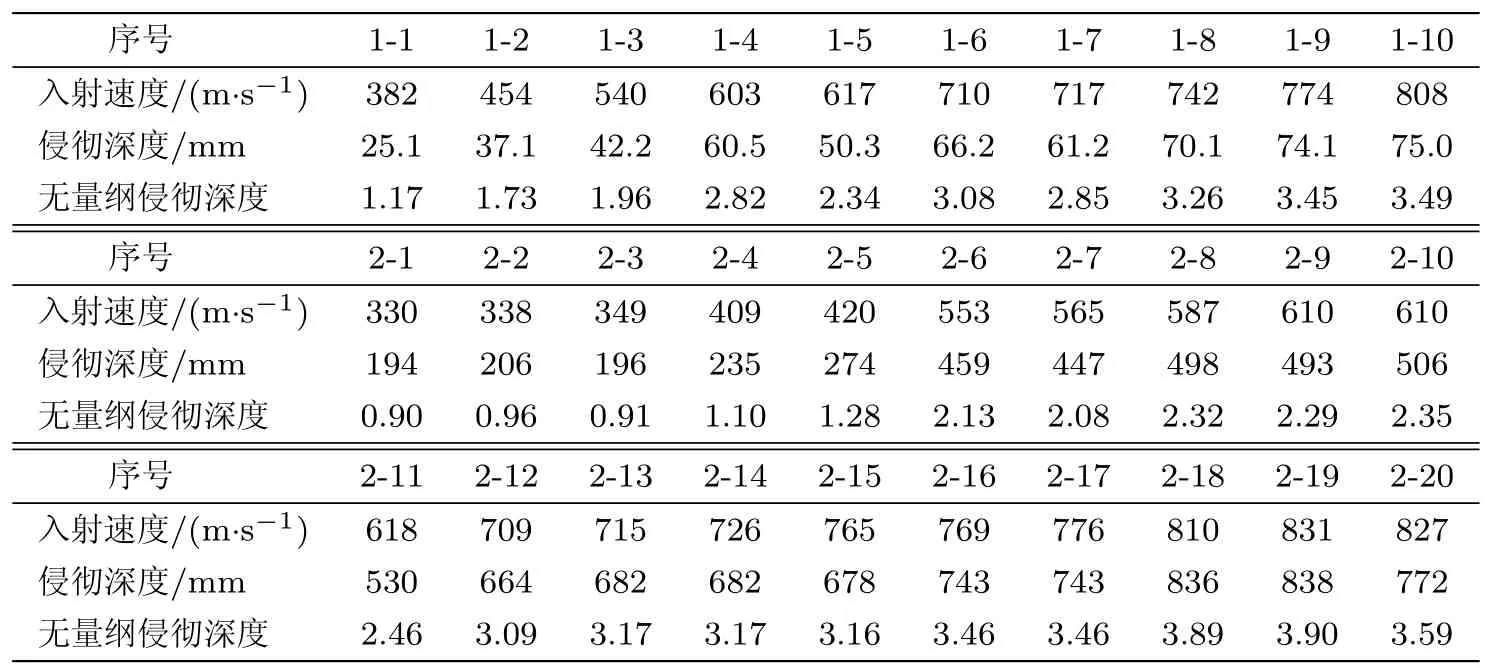
表3 文献 [15]侵彻实验数据

表3中缩比因子为10，原型弹质量5900g，直径76.2mm，靶板 fc为 35.1MPa；缩比弹质量 5.9g，直径7.62mm，靶板fc为34.6MPa；两种弹的CRH值均为3.侵彻速度范围为330∼831m/s，原型弹混凝土靶板抗压强度35.1MPa，缩比弹混凝土靶板抗压强度为34.6MPa.

图 2∼图 4为无量纲侵彻深度随速度变化曲线，从图中可以看到有某种趋势，即所有实验的无量纲侵彻深度曲线同时发生了偏移和偏转，在低速范围内，随着弹体的尺寸的增大，弹体的无量纲侵彻深度也是上升的.这表明在低速范围内，原型弹的无量纲侵彻深度大于缩比弹，这可能是由材料的应变率效应引起的.

图2 文献[13]中无量纲侵深随速度变化

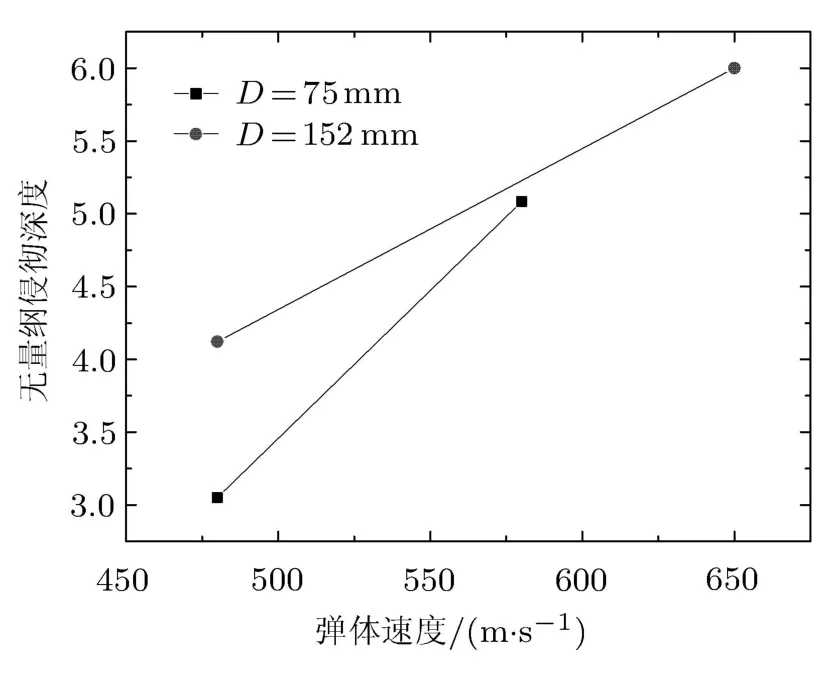
图3 文献[14]中无量纲侵深随速度变化

图4 文献[15]中无量纲侵深随速度变化

图2∼图4中的缩比无量纲侵深曲线和原型无量纲侵深曲线都存在一个交点，说明存在某一个初始弹体速度，在这个速度下，缩比弹和原型弹的无量纲侵彻深度恰好相等.当速度升高达到两族曲线交点后，随着弹体速度的增大，弹体的无量纲侵彻深度接近重合，甚至是降低的，这时原型弹的无量纲侵彻深度小于缩比弹，这可能是由材料的损伤演化引起的.

从表4中可以看出，文献[13]的实验中，无量纲侵彻深度曲线偏转量为7.4%.侵彻速度为500m/s时，徐建波的实验中无量纲侵彻深度曲线偏移量为1.3%，而同一速度下文献[15]的无量纲侵彻深度曲线偏移量为6.3%，说明缩比因子越大，工程实际实验值与几何相似模型值偏离越大.文献 [14]的实验由于弹的质量较大且数据量较少，偏转和偏移得更厉害.以上这些都表明几何相似律是不成立的，这就是侵彻试验的尺度效应.从材料物性的角度出发，造成尺度效应的原因是材料的应变率敏感性和材料的损伤演化.

表4 无量纲侵深曲线分析

3 结论

(1)不考虑材料应变率效应和材料的损伤演化时，当相同弹形几何相似，相同弹靶材料组合和相同的初始速度时，最大侵彻深度 H和弹的尺寸 L成比例.

(2)材料物性考虑时效时，混凝土抗侵彻的几何相似律是不成立的，无量纲侵彻深度曲线会同时发生偏转和偏移，有必要计入材料响应之应变率效应和损伤演化对几何相似律的修正.

(3)弹体速度不同时，无量纲侵彻深度的偏移量有所差别，与缩比因子有关，缩比因子越大，工程实际实验值与几何相似模型值偏离越大.侵彻速度为500m/s时，缩比因子为 2的实验中无量纲侵彻深度曲线偏移量为1.3%，而同一速度下缩比因子为10的无量纲侵彻深度曲线偏移量为6.3%.

1 Feng J,Li WB,Wang XM,et al.Dynamic spherical cavity expansion analysis of rate-dependent concrete material with scale effect.International Journal of Impact Engineering,2015,84:24-37

2 Mazzariol LM,Oshiro RE,Alves M.A method to represent impacted structures using scaled models made of different materials.International Journal of Impact Engineering,2016,90:81-94

3 Qi CZ,Wang MY,Qian QH.Strain-rate effects on the strength and fragmentation size of rocks. International Journal of Impact Engineering,2009,36(12):1355-1364

4 Wen HM,Jones N.Experimental investigation of the scaling laws for metal plates struck by large masses.International Journal of Impact Engineering,1993,13(3):485-505

5 Noam T,Dolinski M,Rittel D.Scaling dynamic failure:a numerical study.International Journal of Impact Engineering,2014,69(4):69-79

6白以龙.工程结构损伤的两个重要科学问题 ––分布式损伤和尺度效应.华南理工大学学报 (自然科学版)，2002，30(11):11-14

7覃悦，文鹤鸣，何涛.锥头弹丸撞击下FRP层合板的侵彻与穿透的理论研究.高压物理学报，2007，21(2):121-128

8罗春涛.计及应变率效应的侵彻力学工程分析方法和数值模拟.[硕士论文].合肥：中国科学技术大学,2006

9 Forrestal MJ,Altman BS,Cargile JD,et al.An empirical equation for penetration depth of ogive-nose projec-tiles into concrete targets.International Journal of Impact Engineering,1994,15(4):395-405

10 Li QM,Chen XW.Dimensionless for mulae for penetration depth of concrete target impacted by a non-deformable Projectile.International Journal of Impact Engineering,2003,28(1):93-116

11陈小伟.动能深侵彻弹的力学设计(I):侵彻/穿甲理论和弹体壁厚分析.爆炸与冲击,2005,25(6):499-504

12蒋东.工程材料的损伤演化表征和破坏规律研究.[博士论文].合肥：中国科学技术大学,2010

13徐建波，林俊德，唐润棣等.长杆射弹侵彻混凝土实验研究.爆炸与冲击,2002,22(2):174-178

14 Larigberg H,Markeset G.High performance concrete penetration resistance and material development.9th International Symposium on Interaction of the Effects of Munitions with Structures,Germany,1999

15 Canfield J,Clator I.Development of a scaling law and techniques to investigate penetration in concrete,NWL Report No.2057,US Naval Weapons Labortory,Dahlgren,VA,1966

SIMILARITY LAWS AND SCALING OF PENETRATION TESTS1)

JIANG Dong∗,†,2)HUANG Ruiyuan†YU Daojian∗ZHOU Gang∗∗,3)∗(Beijing Institute of Space Long March Vehicle,Beijing 100076,China)
†(University of Science and Technology of China,Hefei 230026,China)
∗∗(Northwest Institute of Nuclear Technology,Xi’an 710000,China)

In this paper,the response of the spherical cavity expansion theory is used to analyze the penetration of the target under the impact of the missile,and a general form of the penetration similarity is established based on the dimension theory.The analysis of the existing experimental data of the projectile shows that the non-dimensional penetration depth curve is deflected and shifted for different penetration speeds.With the strain-rate effect and the damage evolution of the material,the geometric similarity laws do not hold true for the brittle materials such as the concretes.It is necessary to introduce a correction of the geometric similarity law to account for the strain-rate effect and the damage evolution of the material.

penetration,similarity laws,scaling

O385

A

10.6052/1000-0879-17-081

2017–03–13收到第1稿，2017–03–26 收到修改稿.

1)博士后科学基金项目(2014M560829)和国家973计划(6133120402)资助.

2)蒋东，博士，主要研究方向为冲击动力学.E-mail:jiangd@ustc.edu.cn

3)周刚，研究员，主要研究方向为爆炸与冲击动力学.E-mail:gzhou@nint.ac.cn

蒋东,黄瑞源,余道建等.侵彻试验尺度效应和相似准则.力学与实践,2017,39(6):561-565

Jiang Dong,Huang Ruiyuan,Yu Daojian,et al.Similarity laws and scaling of penetration tests.Mechanics in Engineering,2017,39(6):561-565

(责任编辑:周冬冬)