整星隔振用磁流变阻尼器神经网络模型1)
2018-01-06潘忠文陈照波
王 檑 潘忠文 王 旭 祁 峰 陈照波
∗(北京宇航系统工程研究所,北京100076)
†(哈尔滨工业大学机电工程学院,哈尔滨150001)
整星隔振用磁流变阻尼器神经网络模型1)
王 檑∗,2)潘忠文∗王 旭∗祁 峰∗陈照波†
∗(北京宇航系统工程研究所,北京100076)
†(哈尔滨工业大学机电工程学院,哈尔滨150001)
为改善星箭界面振动环境,设计六杆隔振平台,采用磁流变阻尼器作为半主动控制元件,替代原有锥壳过渡支架.对整星隔振平台用磁流变阻尼器进行性能测试,得到反映磁流变阻尼器阻尼特性的实验数据.建立具有两个隐含层的反向传播神经网络对阻尼器进行建模,用于预测磁流变阻尼器阻尼特性以及控制系统设计.提出一种串行算法优化网络结构、权值和阈值,保证网络具有较好的泛化能力和稳定性.仿真结果表明,与参数化模型相比,提出的神经网络模型具有较小的训练误差和较强的泛化能力,能够很好地预测阻尼器的阻尼特性.
神经网络模型,磁流变阻尼器,整星隔振平台,粒子群算法,遗传算法
磁流变阻尼器作为一种半主动控制元件,所需能量少,具有较大的阻尼力调节范围,目前已经应用于航空、汽车、船舶、机械和土木等领域[15].将磁流变阻尼器应用在整星隔振领域,已经有相关的报道[69].磁流变阻尼器具有非线性滞回特性,为预测阻尼器阻尼特性和控制系统设计,需建立力学模型进行描述.磁流变阻尼器力学模型主要有参数化和非参数化模型,参数模型按描述方程主要分为三类:以Bingham模型[10]为代表的分段线性模型,以Bouc-Wen模型[11]为代表的微分方程模型,以Sigmoid模型[12]为代表的非线性模型.参数化模型可以模拟正弦激励下阻尼力与速度、位移的关系,需要进行参数辨识,通常需建立在初始假设的基础上.如果初始假设不符合实际或者参数没有合理的约束,可能获得负质量和负刚度等不符合实际的参数[13].非参数化模型主要以神经网络模型[14]为主,利用正弦或随机试验数据进行网络训练,可以避免参数化模型的缺点,且通过在线训练提高模型精度.本文建立具有两个隐含层的反向传播神经网络对阻尼器进行建模.提出一种串行算法优化网络结构、权值和阈值.首先采用粒子群算法优化隐含层节点数,保证网络具有较好的泛化能力;然后利用遗传算法优化神经网络初始权值和阈值,避免网络陷入局部极小值.
1 阻尼特性试验与数据处理
为改善星箭界面力学环境,设计如图1所示的Stewart六杆平台,支杆结构如图2所示,采用磁流变阻尼器和弹簧并联结构,支杆与上下平台采用球铰连接.

图1 整星隔振平台
磁流变阻尼器选择一款LORD公司的磁流变阻尼器,利用INSTRON8802材料性能试验机对磁流变阻尼器进行动力学性能测试.测试前,将磁流变阻尼器安装在材料性能试验机上,如图3所示,为磁流变阻尼器提供恒电流驱动.当材料性能试验机推动磁流变阻尼器动作时,阻尼器活塞与缸体之间的相对位移以及阻尼力由材料性能试验机所安装的位移传感器和力传感器测得,并通过数据采集仪记录并保存.
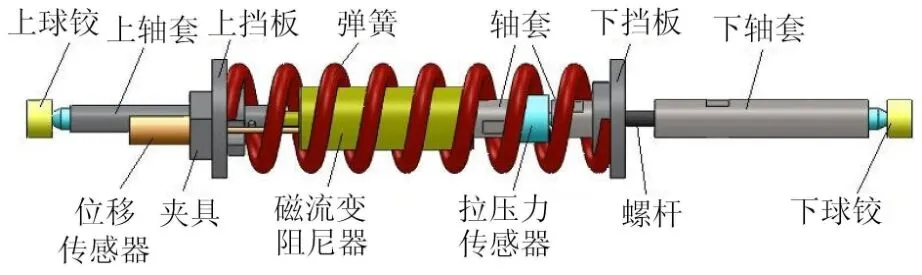
图2 支杆结构

图3 磁流变阻尼器动力特性测试实验
设定材料性能试验机对磁流变阻尼器进行等幅正弦激励,激励频率分别为0.5Hz,1.0Hz,1.5Hz和2.0Hz,激励幅值分别为 5mm,10mm和 20mm,分别输入 0∼1.0A的恒定电流.测量系统采样率为1000Hz,测量时间为30s.
测量位移和阻尼力信号中存在高频量测噪声,需利用低通滤波器将噪声过滤.因为有限长单位冲激响应滤波器具有线性相位,采用这种滤波器,通带频率为0∼20Hz,截止频率 50Hz.采用滤波后的数据对神经网络进行训练和验证.训练和验证数据选择方式如表1所示.

表1 训练数据与验证数据选择方式
2 输入变量选择与网络优化
为保证训练精度,采用具有两个隐含层的误差反向传播神经网络,网络结构如图4所示.
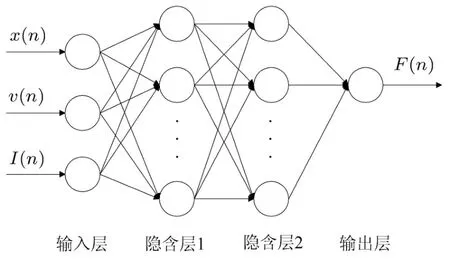
图4 神经网络结构示意图
输入变量的选择对网络训练精度具有较大的影响,进行网络训练前,需要对输入输出数据进行归一化处理,选择的输入变量为阻尼器活塞与缸体相对位移 x(n)、前一时刻相对位移 x(n−1)、相对速度v(n)、前一时刻相对速度v(n−1)和阻尼器驱动电流I(n),输出为阻尼力F(n),初步选择的两个隐层节点数都为15,采用均方误差作为训练目标
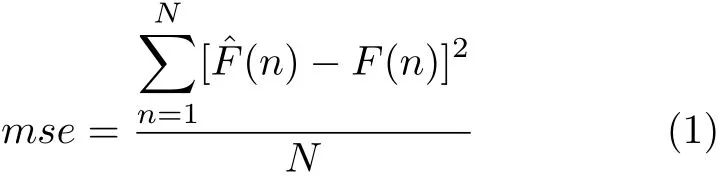
选择不同的输入变量,讨论输入变量对训练结果的影响,训练结果如表2所示.训练结果表明,x(n−1)和 v(n−1)对训练结果影响很小,选择x(n),v(n)和I(n)作为网络输入.采用前向反向传播神经网络,第一个隐含层采用tansig函数作为传递函数,第二个隐含层采用logsig函数作为传递函数,输出层采用线性函数,权值和阈值学习方法为Levenberg--Marquardt(LM)算法.

表2 不同输入组合训练误差
为获得性能更优的网络结构,提出一种串行算法,如图5所示.首先采用粒子群算法优化网络结构,当多次计算结果收敛时,得到两个隐含层节点个数,若结果不收敛,则需修改粒子群算法种群规模和迭代次数,重新计算;得到最优隐层节点数后,为避免网络陷入局部极小值,采用遗传算法获取神经网络最优初始权值和阈值,进一步训练后输出网络.
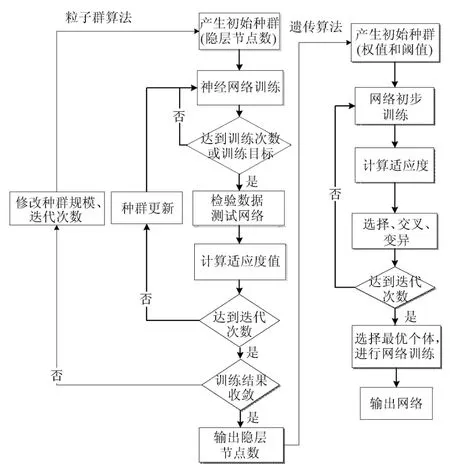
图5 串行算法流程图
通常情况下,节点数目的选择需要根据经验试凑. 本文采用粒子群算法优化两个隐含层节点数目,两个隐含层节点数目记为n1和n2.为了保证训练网络具有较小的训练误差和较好的泛化能力,采用归一化训练数据均方误差和归一化验证数据均方误差的平均值作为适应度函数,即

式中,fitness1是粒子群算法适应度函数值,msex是归一化训练数据的均方误差,msey是归一化验证数据的均方误差.
粒子群算法是一种群体智能优化算法,粒子位置、速度和适应度值三项指标代表粒子特征.算法中每个粒子的位置都代表问题的潜在解,每个粒子对应一个由适应度函数决定的适应度值,该适应度值代表着粒子的优劣.粒子在解空间运动,其速度可以通过跟踪个体极值和群体极值得到,从而更新个体位置.个体极值是指个体所经历位置中计算得到的适应度值最优位置,群体极值是指种群中的所有粒子搜索到的适应度最优位置.粒子每次更新位置,都会得到新的种群,再根据适应度值更新个体极值和群体极值,反复进行,直到达到迭代次数或者适应度值满足要求.算法流程如图6所示.

图6 粒子群算法流程图
选择隐含层节点数目n1和n2为粒子位置,记为[n1,n2],粒子速度计算公式为

式中,S是粒子个数;w,c1,c2是加权系数;r1和r2为0到1之间的随机数;是个体最优位置;是全局最优位置;k为迭代次数.
有的资产管理软件太高级,未考虑到实际工作中的变化和情况的复杂性;有的功能太多反而不利于操作和维护,导致花大价钱投入的高级资产管理系统实用价值和回报有限。
粒子速度由个体最优位置、全局最优位置和上一次迭代速度三部分组成,通过跟踪个体最优位置和全局最优位置,使粒子具有趋向个体最优和全局最优位置的趋势.
位置更新为上一代位置与速度之和,即
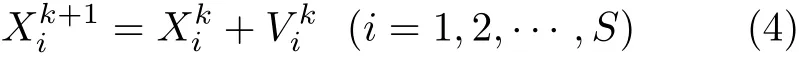
通过速度和位置更新得到新一代个体,搜索过程如图7所示.通过多次迭代后,可以得到最优的隐层节点数,因为神经网络训练结果具有不确定性,每次训练结果可能不同,需经过多轮优化,使计算结果趋于稳定.
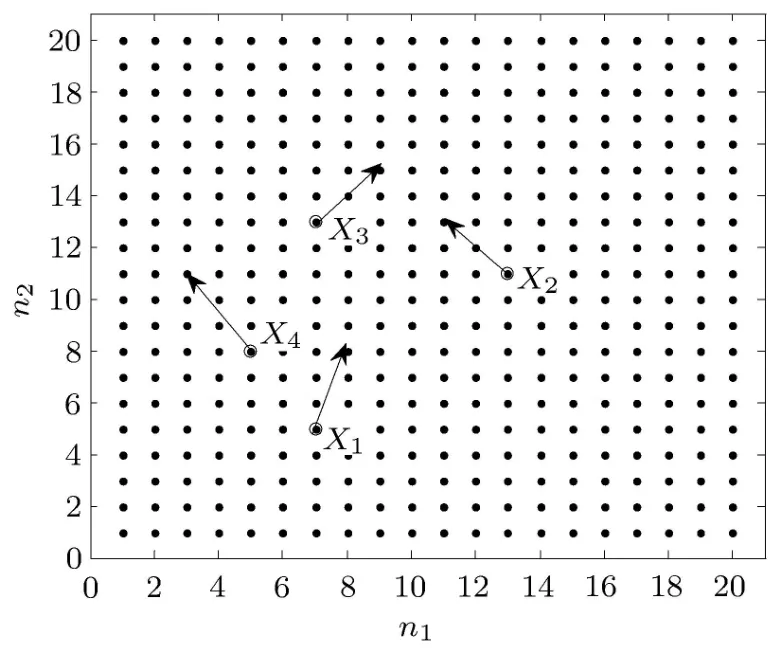
图7 粒子群算法解空间搜索示意图
得到最优网络结构后,需对网络进一步训练.通常情况下,神经网络权值和阈值初始值为随机选取,因而网络容易陷入局部极小值,导致网络训练结果不稳定.针对这一问题,采用具有全局搜索能力的遗传算法获取神经网络最优权值和阈值[15],然后进行网络训练,避免上述问题.
遗传算法是一种随机迭代、进化的搜索方法,它将生物界中的自然选择和种群遗传学原理引入到搜索过程中,通过适应度函数定义个体适应环境的能力,在选择、交叉、变异后产生新的个体,新一代个体保留了上一代个体中的优良基因,同时可能产生更为优良的个体.
采用实数编码形式,个体为网络权值和阈值构成的向量,第i个个体记为ai,其中每个权值或阈值元素代表一个染色体,第i个个体的第k个染色体记为aik,算法流程如图8所示.
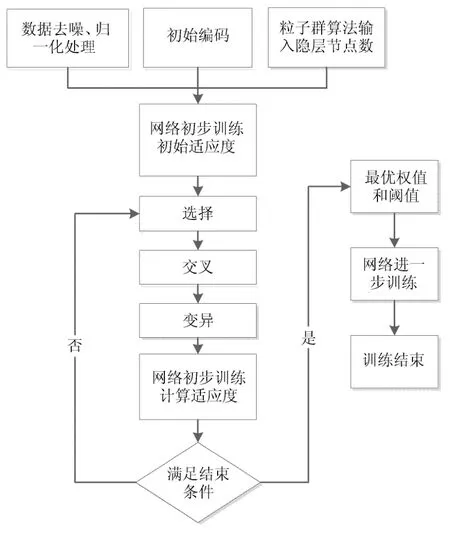
图8 遗传算法流程图
适应度函数为归一化数据训练网络的均方误差,适应度函数值越小,代表个体适应度越高,即
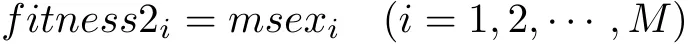
式中M 为个体数,定义 fi=1/fitness2i,即 fi越大,个体适应度越高.
选择操作:采用轮盘赌法,即基于适应度比例的选择策略,第i个个体的选择的概率为

交叉操作:采用实数交叉法,两个个体相互交叉,为选择一个随机位置处的染色体,进行交叉操作.设选择第i个和第j个个体的第k个染色体进行交叉,则交叉操作为

式中,b为0到1之间的随机数.
变异操作:选择第i个个体的第j个染色体aij进行变异,操作为

式中,f(g)=p(1−g/G)2,p和 r为0到 1之间的随机数,G为最大进化次数,g为当前进化次数,即随着进化次数逐渐增加,变异率逐渐降低,以保证优良个体不遭淘汰.
通过上述迭代过程,得到网络最优初始权值和阈值,然后进一步训练网络,得到最优神经网络.
3 仿真结果
隐层节点数范围选为 1∼40,为保证训练结果的准确性,进行三次迭代计算,训练结果如表3所示.表中隐层节点数分别收敛到 [39,18],[40,19]和[39,15],说明算法已经基本收敛.同时每次计算结果中训练误差和验证误差基本保持同一水平,从而保证了网络具有较强的泛化能力.粒子群算法的适应度曲线和最优个体轨迹如图9和图10所示.

表3 粒子群算法计算结果
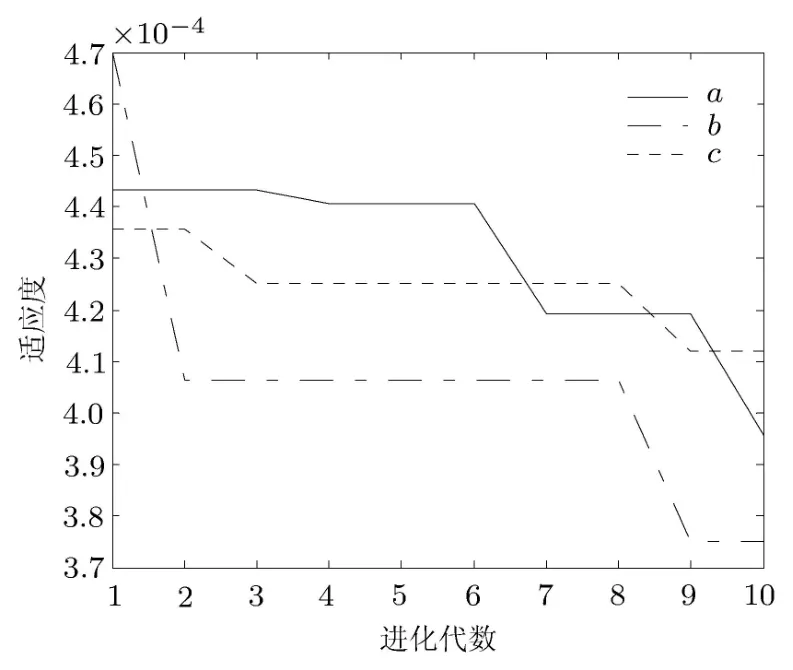
图9 粒子群算法适应度曲线

图10 粒子群算法最优粒子轨迹
内层遗传算法的适应度曲线如图11所示,随着进化代数增加,种群最优适应度值逐渐减小.对遗传算法获取初值和随机生成初值进行比较,如表4所示.数据表明采用遗传算法获取最优初始权值和阈值具有更小的训练误差和验证误差,验证了算法的有效性.

图11 遗传算法适应度曲线

表4 遗传算法获取初值与随机生成初值训练结果比较
神经网络训练结果与验证结果如图12所示,速度滞回特性如图13所示,可以看出,神经网络模型可以较好地预测磁流变阻尼器力学特性.
为验证神经网络模型的准确性,将神经网络模型预测结果与应用较为广泛的参数化模型进行比较.选取双曲正切模型[16]和双Sigmoid模型[12],比较结果如图14所示,可以看出,神经网络模型预测结果要优于双曲正切模型和双Sigmoid模型,能够在细节上捕获磁流变阻尼器阻尼特性,验证了神经网络模型的优越性,将其应用在控制系统设计与仿真中,用来预测阻尼器的阻尼力,可以设计出性能更优的控制系统.
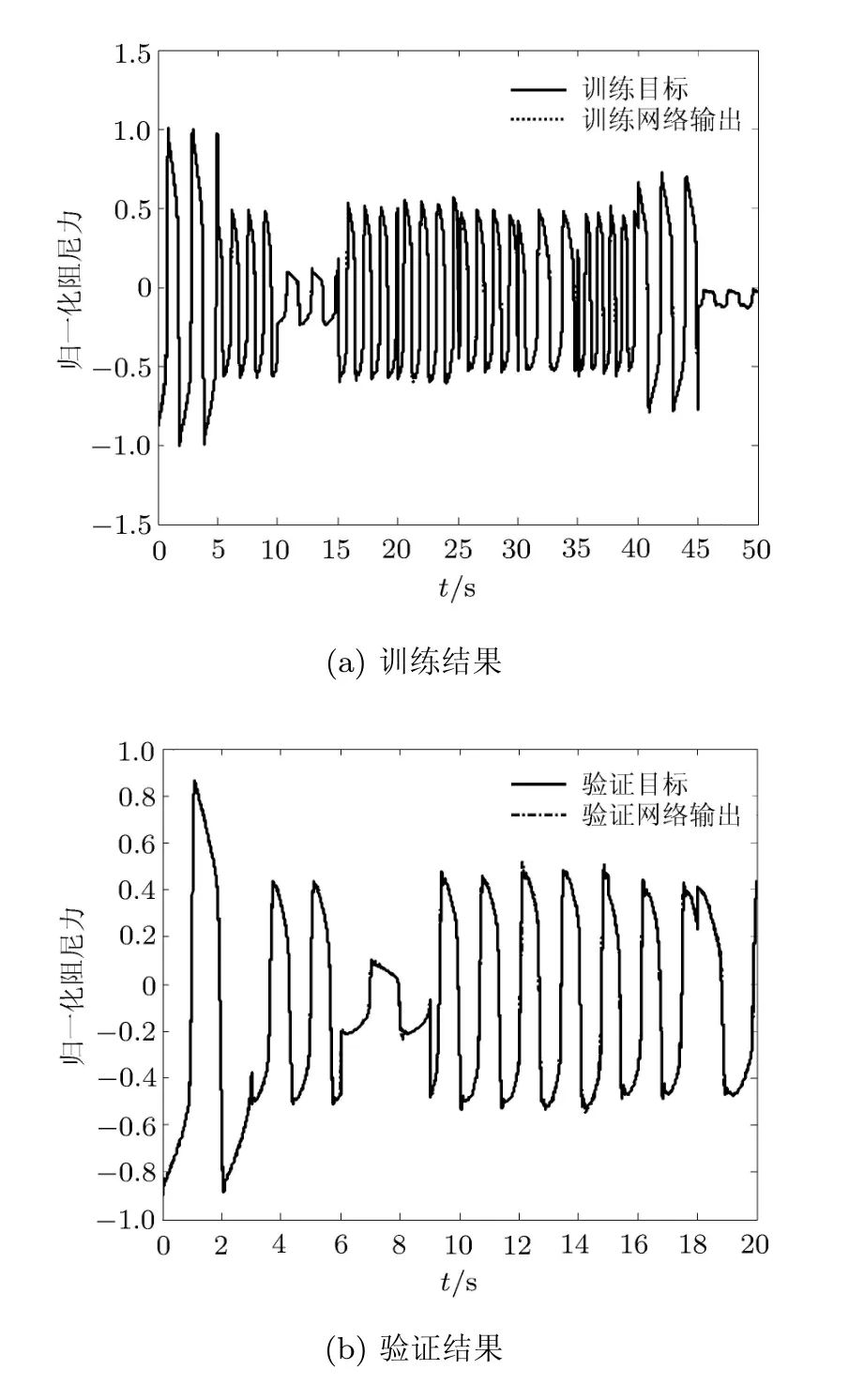
图12 归一化数据训练结果与验证结果

图13 速度滞回特性预测效果

图14 预测效果对比
4 结论
对整星隔振用磁流变阻尼器进行性能测试,得到阻尼力与位移试验数据.建立具有两个隐含层的神经网络模型,采用粒子群算法优化隐含层节点个数,并用遗传算法获取最优初始权值和阈值.仿真结果表明,与现有参数化模型相比,神经网络模型具有更高的预测精度,能够在细节上捕捉磁流变阻尼器阻尼特性.神经网络模型在实际工作中可以作为传感器使用,以降低成本和减轻结构重量,同时在控制系统仿真中可以更真实地反映磁流变阻尼器的阻尼特性,得到的仿真结果更加真实有效,有利于控制系统的设计,具有重要的工程应用价值.
1王唯,夏品奇.采用磁流变阻尼器的直升机 “地面共振”分析.南京航空航天大学学报,2003,35(3):264-268
2廖昌荣,余淼.汽车磁流变减振器设计中值得注意的若干技术问题.汽车技术,2001,(5):11-14
3周云,吴志远,梁兴文.磁流变阻尼器对高层建筑风振的半主动控制.地震工程与工程振动,2001,21(4):159-162
4王锎,磁流变阻尼器控制双跨转子轴系振动研究.振动与冲击,2015,34(2):150-153
5田正东,姚熊亮.基于MR的船用减振抗冲隔离器力学特性研究.哈尔滨工程大学学报,2008,29(8):783-788
6涂奉臣,基于磁流变阻尼器的整星半主动隔振技术研究.[博士论文].哈尔滨:哈尔滨工业大学,2010
7 Jean P,Ohayon R,Bihan DL.Semi-active control using magnetorheological dampers for payload launch vibration isolation. Smart Structures and Materials,2006,6169:61690H-18 Unsal M.Semi-active vibration control of a parallel platform mechanism using magnetorheological damping.[PhD Thesis].Florida:University of Florida,2006
9程明,陈照波.应用磁流变技术的星箭界面半主动隔振研究.振动工程学报,2017,30(1):86-92
10 Stanway R,Sproston JL,Stevens NG.Non-linear modeling of an electro-rheological vibration damper.J Eletrostatics,1987,20:167-184
11 Spencer BF,Dyke SJ,Sain MK,et al.Phenomenologial model for magnetorheological dampers.J of Eng Mech,1997,123(3):230-238
12李秀岭,李宏男.磁流变阻尼器的双sigmoid模型及试验验证.振动工程学报,2006,19(2):168-172
13 Truong DQ,Ahn KK.Nonlinear black-box models and force-sensorless damping control for damping systems using magetorheological fluid dampers.Sensors and Actuators A:Physical,2011,167:556-573
14 Batterbeea DC,Simsa ND.Temperature sensitive stability of feedback controllers for MR dampers.Active and Passive Smart Structures and Integrated Systems,2008,6928:277-786
15王小川,史峰.MATLAB神经网络43个案例分析.北京:北京航空航天大学出版社,2013.20-32
16 Kwok NM,Ha QP,Nguyen TH,et a1.A novel hysteretic model for magnetorheological fluid dampers and parameter identification using particle swarm optimization.Sensors&Actuators A Physical,2006,132(2):441-451
NEURAL NETWORK MODEL OF MAGNETORHEOLOGICAL DAMPER FOR VIBRATION ISOLATION PLATFORM OF WHOLE-SPACECRAFT1)
WANG Lei∗,2)PAN Zhongwen∗WANG Xu∗QI Feng∗CHEN Zhaobo†
∗(Beijing Institute of Space System Engineering,Beijing 100076,China)
†(School of Mechatronics Engineering,Harbin Institute of Technology,Harbin 150001,China)
To improve the interface vibration environment of the satellite and the rocket,a six-pole vibration isolation platform is built,with the magnetorheological damper as the semi-active control device.The magnetorheological damper for the whole vibration isolation platform is tested to obtain the experimental data for the damping characteristics of the magnetorheological damper.The BP(back propagation)neural network with two hidden layers is established to model the damper for predicting the damping characteristics of the magnetorheological damper and for the design of the control system.A sequential algorithm is proposed to optimize the network structure,the weight and the threshold to ensure that the network has a better generalization ability and the stability of the network training.The simulation results show that compared with the parametric model,the proposed neural network model has less training error and higher generalization ability,and can well predict the damping characteristics of the damper.
neural network model,magnetorheological damper,whole-spacecraft vibration isolation platform,particle swarm algorithm,genetic algorithm
本文于 2017–06–28收到.
1)国家自然科学基金(11372083)和中国运载火箭技术研究院创新基金资助项目.
2)王檑,研究生,主要研究方向为载荷与力学环境.E-mail:2504123264@qq.com
王檑,潘忠文,王旭等.整星隔振用磁流变阻尼器神经网络模型.力学与实践,2017,39(6):579-584
Wang Lei,Pan Zhongwen,Wang Xu,et al.Neural network model of magnetorheological damper for vibration isolation platform of whole-spacecraft.Mechanics in Engineering,2017,39(6):579-584
O328
A
10.6052/1000-0879-17-234
(责任编辑:周冬冬)
