直角三角形内接最大正方形(矩形)的优化解法

陈佩宁， 张明虎

(石家庄职业技术学院 信息工程系，河北 石家庄 050081)

直角三角形内接最大正方形(矩形)的优化解法

陈佩宁， 张明虎

(石家庄职业技术学院 信息工程系，河北 石家庄 050081)

通过两种不同解法的理论推证，讨论了直角三角形内接最大正方形和最大矩形的优化方法是以直角三角形的两条平行直角边的中位线为切割线.论证了直角三角形内最大正方形面积小于最大矩形面积.

直角三角形；内接；正方形；矩形；优化

有关直角三角形内接最大正方形(矩形)的问题因其具有理论和实践意义，中学和部分高校教材都有涉及.本文试图从理论角度对这一问题进一步探讨，并给出直角三角形内接最大正方形(矩形)的优化方法.

1 直角三角形内接最大正方形解法分析

例1 在一个横截面为直角三角形的原料上，切割一个正方形工件.已知斜边边长为10 cm，一个锐角θ=30°.(1)求正方形的最大边长及面积；(2)画出切割示意图[1].

1.1 教材解法

教材解法示意图见图1.

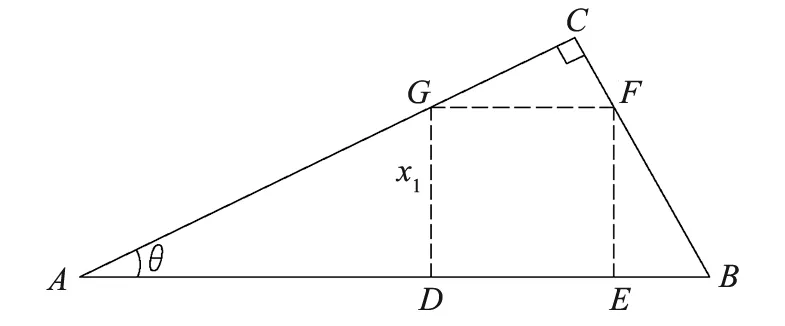
图1 内接最大正方形教材解法示意图

设正方形边长为x1，面积为S1，则

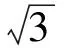
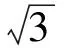
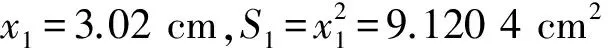
1.2 优化解法

优化解法示意图见图2.

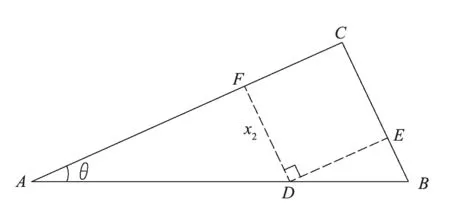
图2 内接最大正方形优化解法示意图

设正方形边长为x2，面积为S2，则

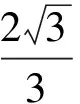
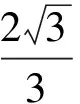
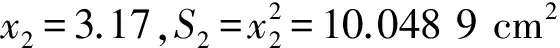
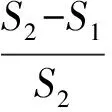
1.3 优化解法的数学依据

此两种解法均不失一般性，问题可归纳为已知直角三角形的斜边长度和一个锐角θ(0<θ<90°)，求这个直角三角形内接最大正方形的边长及面积，并作出图形.

假设AB=c，∠A=θ，求正方形DEFG的面积.

1.3.1 教材解法思路

解法示意图见图1.

解： 设DG=x1， 则AD=x1cotθ，DE=x1，

EB=x1tanθ.

由AD+DE+EB=AB,

即x1cotθ+x1+x1tanθ=c，

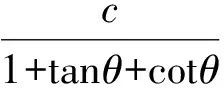
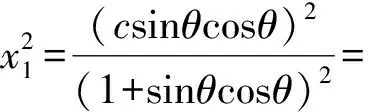
(1)

1.3.2 优化解法思路

解法示意图见图2.

设所求正方形DECF边长为x2，AD=x2cscθ,DB=x2secθ，由AD+DB=c,得x2cscθ+x2secθ=c

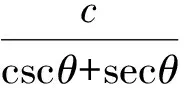
(2)

(3)

由公式(1)和公式(3)，可知S2>S1.

1.4 优化解法转化方案分析

确定一个直角三角形，可以转化为已知这个直角三角形的一个锐角θ和θ所在的直角边.据此，给出下文的解法，与优化解法做进一步比较.

例2 已知直角三角形中，∠A=θ,AC=b，求正方形CEDF的边长及面积S正.(见图3)

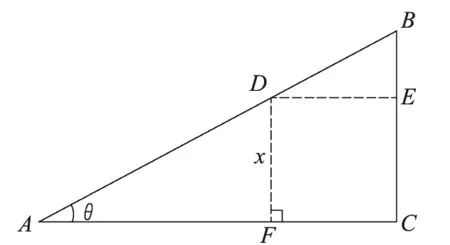
图3 内接最大正方形优化解法转化方案示意图

解：设FC=FD=x，则AF=FDcotθ=xcotθ

由AF+FC=b，得

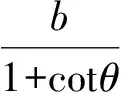
(4)

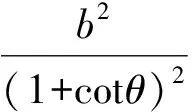
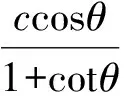
2 直角三角形内接最大正方形的优化方案

通过上述分析计算，给出优化方案如下：

1)测定直角三角形的一个锐角θ值，测定(或计算)这个锐角θ所在的直角边的边长b.

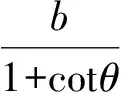
3 直角三角形内接最大矩形分析及优化

3.1 教材解法

教材解法示意图见图4.

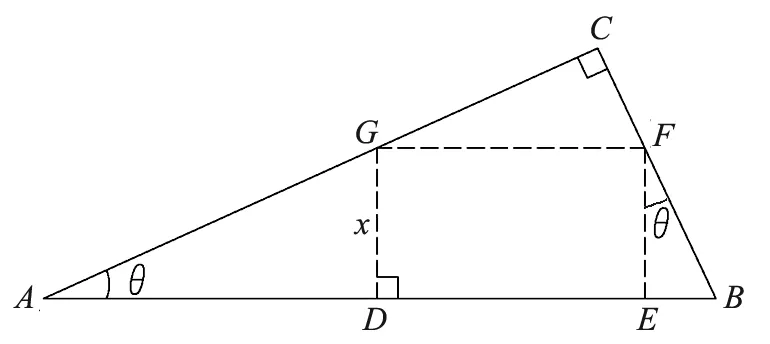
图4 内接最大矩形教材解法示意图

已知∠A=θ,AB=c，求矩形DEFG的最大面积S矩.

解：设DG=x，则AD=xcotθ，EB=xtanθ，

DE=c-x(cotθ+tanθ)

(5)

S矩=DG×DE=cx-x2(cotθ+tanθ)

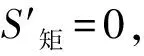
(6)

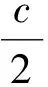
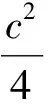
3.2 优化解法

优化解法示意图见图5.

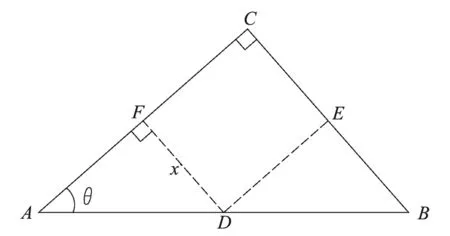
图5 内接最大矩形优化解法示意图

设DF=x，AC=a,BC=b,则AD=xcscθ,

DB=AB-AD=c-xcscθ,

DE=DB·cosθ=(c-xcscθ)cosθ=

ccosθ-xcotθ

(7)

S矩=DF×DE=ccosθ·x-x2cotθ

(8)

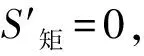
(9)

将(9)式代入(8)式得,

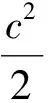
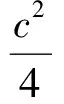
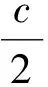
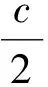
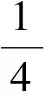
(10)

总之，两种解法均利用了求导判断，所得结果是最大矩形.两种解法结果一致，最大矩形面积是所论直角三角形面积的一半.解法二优于解法一的理由是结果的几何意义清晰，便于切割加工.

在直角三角形内割取最大矩形的优化方法，是以直角三角形的两条平行直角边的中位线为切割线.

4 直角三角形内接最大正方形与矩形面积的大小关系

由(10)式得,

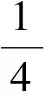
(11)

由(3)式得,

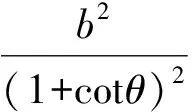
(12)

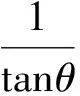
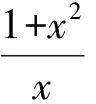
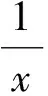
所以S矩≥S正.当tanθ=1时，即θ=45°时，S矩=S正.

通过以上讨论，可以得到割取直角三角形内接最大正方形和内接最大矩形的优化方法，并论证了同一直角三角形内接最大正方形面积小于最大矩形面积.

[1] 牛铭.工科应用数学[M].北京:中国铁道出版社，2016：4.

Anoptimizationmethodofthelargestsquareorrectangleinarighttriangle

CHEN Pei-ning, ZHANG Ming-hu

(Department of Information Technology, Shijiazhuang University of Applied Technology, Shijiazhuang, Hebei 050081, China)

This paper discusses the optimization of the largest square or rectangle in a right triangle by two different methods, and proves the area of the largest square is less than that of the rectangle.

right triangle; inscription; square; rectangle; optimization

2017-03-24

陈佩宁(1971-)，女，河北望都人，石家庄职业技术学院讲师.

1009-4873(2017)06-0078-03

O241

A

吴瑞红