基于Optistruct软件的翼子板刚度、模态的分析及优化

刘家员， 王可洲， 周 伟

(1.辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001；2.山东农业工程学院 机械与电子工程学院，山东 济南 250100； 3.中国重汽集团 办公室，山东 济南 250000)

基于Optistruct软件的翼子板刚度、模态的分析及优化

刘家员1， 王可洲2， 周 伟3

(1.辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001；2.山东农业工程学院 机械与电子工程学院，山东 济南 250100； 3.中国重汽集团 办公室，山东 济南 250000)

运用有限元分析法，基于Optistruct软件对某车型前翼子板刚度及其模态进行分析.翼子板有限元模型建立要求为：模型导入、几何清理、网格划分、网格质量检查、载荷及工况加载.模型分析结果显示铝合金材料翼子板的刚度较大，耐冲击能力较强，安全系数较高，相比于复合材料翼子板优势明显.优化方案设计将质量以及静态位移作为响应，设置静态位移为约束点，最小限度为1 mm；对于局部应力点加强约束或者加入加强筋板.

翼子板；铝合金材料；复合材料；刚度；模态；Optistruct

翼子板作为汽车的覆盖件，将外板部和加强部形成一体，其中外板部露出车辆侧面，加强部沿配置部件边缘延伸，形成邻接部件的配合部.在汽车翼子板的设计中，常关注翼子板的振动以及刚度对汽车运行的影响.翼子板是汽车车身一个较小的部件，也是汽车车身外覆盖重要部件之一[1].翼子板是由复杂的曲面构成，对于汽车设计的要求较高，传统的经典力学设计分析复杂工况会带来计算冗长、精确度低、工作强度大等问题[2]，基于计算机辅助工程基础的设计能提高效率、缩短开发周期、减少开发成本.笔者以某公司的实际仿真项目为基础，运用有限元分析法模拟真实实验，运用Hypermesh作为前处理、Optistruct作为求解器、Hyperview作为后处理器，对某车型翼子板刚度及其模态进行分析，找其薄弱环节，为设计人员提供优化建议.

1 模态分析理论概述

1.1 模态分析理论简介

模态分析理论是在20世纪30年代，基于机械阻抗与导纳的概念上发展起来的理论，同时借鉴了振动理论、信号分析、数据处理、数理统计、自动控制等有关理论，形成一套有特色的理论体系.

模态分析是将线性时不变系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，坐标变换的变换矩阵为振型矩阵，其每列即为各阶振型[3].

有限元模态分析是建立在模态模型数值分析的基础上的，模态的求解过程是在无阻尼、无外载情况下的模态矢量，但是对于结构模态来说可以忽略模态频率和振型的影响，结构模态是材料本身的特殊性决定的，与外载或初始条件无关[4].

1.2 N自由度线性分析方程

N自由度线性系统微分方程对于N阶线性系统，其运动微分方程表达如下：

(1)

由于模态分析法是利用无阻尼的主振型对应的模态坐标进行分析，所以需要对公式(1)进行解耦，对公式(1)进行拉氏变换得：

(s2M+sC+K)X(s)=f(s)

(2)

其中，s为拉氏变换因子；X(s)为位移响应；f(s)为拉氏变换激励.

任意L点的响应为各阶模态响应的线性组合，引入模态坐标Q:

xl(ω)=φl1q1(ω)+φl2q2(ω)+

其中，xl(ω)为频域下的位移响应，φlr为L点的第r阶的振型系数，qr(ω)为第r阶的模态坐标.

Φ=[φ1φ2…φN](振型矩阵),

Q={q1(ω)q2(ω)…qN(ω)}T(模态坐标).

则有：X(ω)=ΦQ，

(K-ω2M+jωC)ΦQ=F(ω).

其中，F(ω)为频域下的激振力;jω为等量替换式;ω为角速度.

2 翼子板有限元建模分析

2.1 Hyperworks 软件简介

Hyperworks是美国Altair公司开发的系列计算机辅助工程分析软件，本研究运用的Hypermesh是一个高性能前处理器.在国内市场上，Hypermesh作为前处理占到50%以上，成为国内汽车领域工程分析常用的分析软件[5].Optistruct 是Hyperworks 产品中的结构分析和优化工具，是Altair公司旗下比较著名的结构分析求解器，本研究主要运用此工具作为求解器.

2.2 建立翼子板有限元模型

建立有限元模型时尽量保持所有的特征线，这样结果会更准确，单元尺寸定为8 mm，对于圆角部分依然保持不变，将翼子板的7个安装孔处创建垫圈，保证网格的质量.有限元模型建立基本流程见图1.

(1)模型导入

模型建立文件为Step文件，在Hypermesh中导入，由于Step文件属性决定模型建立后失真程度几乎为零，所以导入后对于原几何几乎不用修改，直接应用即可.

图1 有限元模型建立基本流程

(2)几何清理

对几何抽取中面直接处理，7个安装孔加垫圈处理.由于翼子板所画网格为8 mm，则对于1～2 mm的圆角影响到网格质量的线合并或直接处理掉，在保证不影响分析的情况下将太小的孔直接去掉.

(3)网格划分

网格划分是有限元分析中最为重要的一步，也是最基础的一步，网格划分的好坏直接影响到分析质量.本模型直接在处理的中面上采用混合类型划分网格.由于三角形本身就有稳定性，在分析中会增加模型的刚度，分析的失真度增加，所以在划分网格时要合理控制三角形的数量.采用铝合金材料，同时用复合材料作对比，将内板和外板用包边作连接处理.本模型网格划分结果为：整体划分节点数为8829个、网格数为8542个.建立的有限元模型见图2.

图2 有限元模型

(4)网格质量检查

对于有限元分析来说，网格质量检查主要是针对网格的雅克比、长宽比、三角形最大角度、四边形最小内角值的检查.其中，网格划分的雅克比最小值为0.31，四边形最小内角为20.68°，三角形最大内角119°.

(5)载荷及工况加载

此翼子板采用螺栓的连接方式，通过Hypermesh做前处理，用刚性体模拟真实环境中的螺栓，在螺栓孔中施加约束为6自由度，建立边界条件卡片，设置为模态类型，在5个不同的位置抓取面积为25 mm×25 mm的刚性区域，建立局部坐标，通过局部坐标添加相同大小的法向力，以模拟与其他部件的非螺栓连接的受力情况.本模型主要以铝合金材料翼子板和复合材料翼子板为例分析，并通过对比给出相应的结论.铝合金材料翼子板(AL)和复合材料翼子板(SMC)基本参数见表1.

表1 铝合金材料翼子板和复合材料翼子板基本参数

3 翼子板的模态及结构分析

3.1 翼子板模态分析

将设置好的模态及刚度选项卡片的载荷工况提交给Optistruct求解器求解，通过Hyperview后处理软件得到模态分析云图，如图3所示.

图3 模态分析云图

从模态云分析图可以看出，模态是从非约束的地方开始蔓延到内部，实际蔓延的趋势不大.铝合金翼子板十阶模态的数值见表2.

振动模态是在无阻尼状态下测得的，计算车身的固有频率和振型，就可知道与其他系统的干扰程度.通过合理设计，会改善或消除共振的可能性，一般情况下车身结构整体一阶模态频率越高越好[6].

表2 铝合金材料翼子板十阶模态数值

铝合金材料翼子板与复合材料翼子板作对比分析时，只需要对比第一阶固有频率即可.复合材料翼子板十阶模态见表3.复合材料翼子板第一阶模态数值为42.9 Hz.本次模型分析是某主机厂试车翼子板，一阶模态目标值为50 Hz以上，按照模型数据分析结果选择铝合金材料翼子板.

表3 复合材料翼子板十阶模态数值

3.2 翼子板结构刚度分析

在铝合金材料翼子板件的5个不同位置施加50 N法向力，并对7个安装孔施加6自由度的约束，法向力位置和约束位置见图4和图5.经过Hyperview后处理器处理得到位移云图和应力云图，取第5个位置的位移和应力云图，如图6和图7所示.

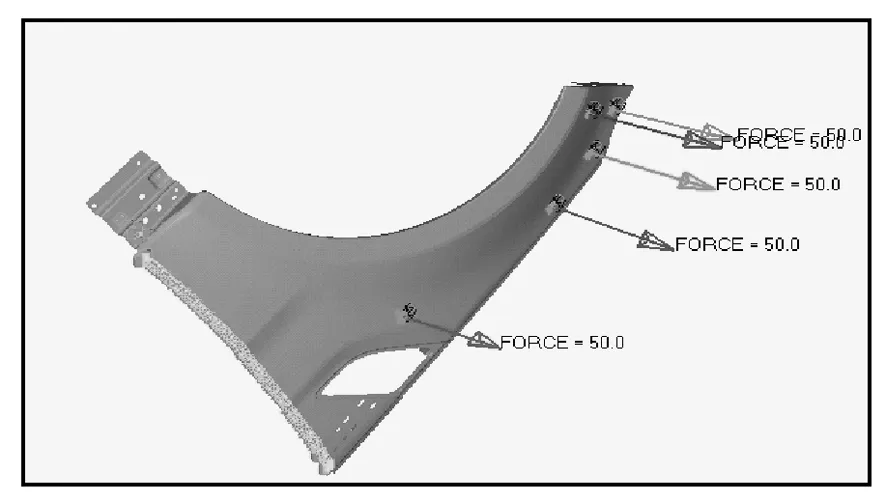
图4 法向力位置

图5 约束位置

图6 位移云图

图7 应力云图

从图6可以看到，铝合金材料翼子板在某点的最大位移量值为3 mm，其节点号为3392.从图7可看出铝合金材料翼子板在某点的最大应力值为78.8 MPa,其节点号为6677.但是总体来说，其应力值都小于翼子板材料的屈服极限值.对铝合金材料翼子板和复合材料翼子板的5个不同位置的刚度、应力、安全系数进行模拟，具体数值见表4.

由表4可以看出，铝合金材料翼子板的刚度、应力较大，耐冲击的能力较强，并且其安全系数也较高，相比于复合材料翼子板优势明显.

4 优化分析

汽车在设计过程中，为了增加强度和稳定性，要将翼子板尽可能多地施加约束或者连接固定件等，还可以将模态首先延伸的部位增加强件.同时翼子板为达到轻量化的目的，可以将应力或位移不大的地方采用简化模型的处理方式.对于整个翼子板来说，如果减小其整体厚度，则必须对局部集中大应力区加以改进.

表4 铝合金材料和复合材料翼子板不同位置模拟数值

基于Altair平台的优化板块中给出铝合金材料翼子板的优化分析结果，如图8所示.此优化方案将质量以及静态位移作为响应，这是由于金属板材的翼子板在质量方面不占优势，铝合金材料翼子板计划设置厚度为1.2 mm,现优化方案设计将静态位移作为约束点，最小限度设置为1 mm.对于局部应力点加强约束或者加入加强筋板等措施.为达到轻量化的目的，根据优化结果，在翼子板本身出现应力几乎为零的地方，进行轻量化设计.

5 结语

通过模态以及结构刚度的分析，对于选择铝合金材料还是复合材料的翼子板，在分析时主要以第一阶模态作为参考，通过大量的仿真实验数据可以看出，铝合金材料的模型会更胜一筹.随着汽车的发展以及技术的要求，轻量化设计将成为主流趋势，通过对模态云图或者位移以及应力云图的分析，在未施加约束的地方往往是翼子板的薄弱环节.所以，如何克服结构中的薄弱环节达到轻量化设计的目的是后期研究者所要关注的重点.

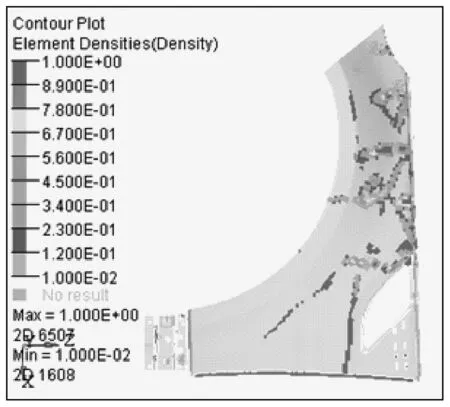
图8 铝合金翼子板的优化分析

[1] 冯晋祥.汽车构造[M].北京：人民交通出版社,2007：245-247.

[2] 解跃青,雷雨成.商务用车车身有限元建模及分析[J].机械设计与制造,2002,2(2):52-53.

[3] 王钰栋,金磊,洪清秀,等.Hyperview & Hyperview应用技巧与高级实例[M].北京:机械工业出版社,2012:295-299.

[4] 胡振,马哲树,冯国增.柴油机曲柄模态的三维有限元分析[J].科学技术与工程,2008,8(2):491-502.

[5] 王晓慧,郑海峰,刘昊鹏,等.基于Hyper Works的折叠翼结构优化设计[J].固体火箭技术,2012,35(6):795-798.

[6] 张胜兰,严飞.基于Hyperworks的车架模态分析[J].机械设计与制造,2005,2(4)：10-11.

Structure,modeandoptimizationoftheOptistruct-basedsoftwareforcarfenders

LIU Jia-yuan1, WANG Ke-zhou2, ZHOU-Wei3

(1. School of Auto Engineering, Liaoning College of Technology, Jinzhou, Liaoning 121001, China;2. School of Mechanics and Electronics, Shandong College of Agricultural Engineering, Jinan, Shandong 250100, China;3. Office, China Sinotruk Group, Jinan, Shandong 250000,China)

This study describes Optistruct-based analysis of the stiffness and finite element modes on auto fenders in relation to the import, geometrical cleaning, mesh clarification, quality control, working loads and conditions. Results show that stiffness of aluminum alloy material is more intense, impact resistance stronger, and safety index higher. That is superior to composite fenders. Moreover, optimization is done in designing with quality and static displacement as response, the static displacement as constraint within a minimum of 1 mm to join a local stress point to reach the goal of lightweight. Where there is zero of a local stress point, the lightweight design is possible.

fender; aluminum alloy; composite material; stiffness; modal; Optistruct

2017-05-26

刘家员(1991-)，男，山东日照人，辽宁工业大学2015级车辆工程专业在读硕士研究生；

王可洲(1965-)，男，山东济南人，山东农业工程学院讲师；

周 伟(1989-)，男，山东日照人，中国重汽集团工程师.

1009-4873(2017)06-0001-05

U463.99

A

吴瑞红