典型飞行器线角复合振动环境再现技术

张文伟，赵朋飞，庞家志，李果



典型飞行器线角复合振动环境再现技术

张文伟，赵朋飞，庞家志，李果

（航天科工防御技术研究试验中心，北京 100854）

为在实验室条件下再现某飞行器系统经历的线振动与角振动复合环境，在分析实测飞行环境数据的基础上，采用虚拟响应点方法对试验控制波形进行解算；通过搭建专用试验系统，采用时域波形复现的方法实现了线角复合振动的间接控制。试验结果表明：该模拟试验方法在频率1000Hz以内能够较好地复现飞行器的飞行环境特征，为再现外场振动环境提供有效的解决途径。

飞行环境；线角复合振动；时域波形复现；双台激励

0 引言

某飞行器系统在使用过程中受到的各种激励力以及发动机传来的强烈振动激励，如随机线振动及角振动，会对飞行器关键系统的性能造成严重影响[1-3]。例如：飞行器系统惯组、导引头等敏感组件在工作时会因这些高频振动的强烈干扰而导致末制导系统的稳定性和精度受到影响，甚至是目标从导引头很小的瞬时视场中丢失[4]。为确保飞行器在这种恶劣的线角复合振动环境下的工作精度与可靠性，需要在地面实验室进行充分的环境模拟与验证试验，再现飞行器线角复合振动的环境效应，尽可能暴露飞行器产品的设计及工艺缺陷，并通过改进不断提高产品的飞行环境适应性及可靠性。

本文提出一种实验室条件下考核飞行器关键分系统性能的线角复合振动环境再现技术。首先，根据飞行器结构特点、受载及边界条件设计并搭建线角复合加载的试验系统；其次，通过飞行振动环境数据分析，采用虚拟响应法对测试点的线角振动量进行解算，并利用二维传递率矩阵和激励反推识别方法对试验控制谱进行合成和修正；最后，采用间接振动控制的时域波形复现方法对飞行器系统进行模拟试验验证，并通过地面测试数据与外场遥测数据的对比分析，评估试验模拟的真实性。

1 线角复合振动试验方案

相对于单输入单输出控制的随机振动试验，多输入多输出（MIMO）控制的随机振动试验因能更好地模拟产品经历的真实环境从而提高对产品潜在缺陷的激发能力，而得到了国内外学者的广泛关注和工程应用[5-9]。由于线振动与角振动复合环境涉及两个自由度，必须采用两点激励的方式才能进行有效模拟；当实测线角复合振动环境呈现非稳态随机特征时，可以采用MIMO时域波形复现方法进行实验室模拟。本次试验研究设计的线角复合振动试验系统如图1所示，其中：4（向）为线振动响应测点，控制点1（向）和2（向）位于试件安装平台上；1、2、3为用于测量角振动的测点；试验件、工装及安装平台通过橡胶绳进行弹性悬挂，保证试验时振动台基本不受静载力的作用，并有利于保持球形解耦装置试验工作姿态的稳定。为确保试件在振动试验中的安全，采用两点固支的方式安装试件。

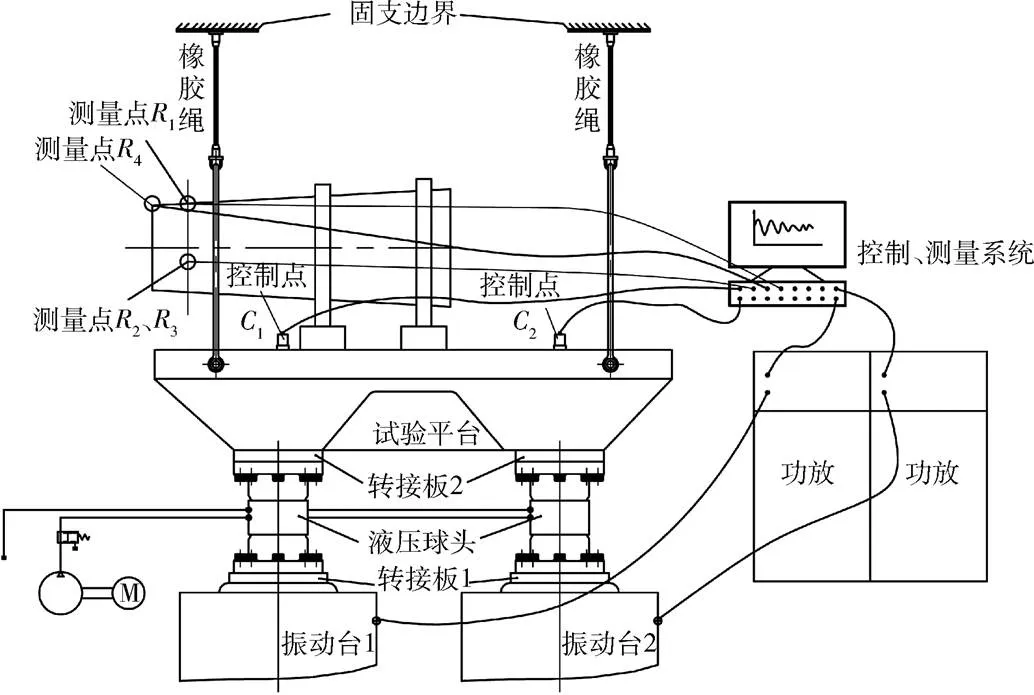
图1 线角复合振动试验系统示意

选取飞行器角振动敏感部件所处的横截端面作为角振动测量的测量面，在进行角振动测量时此截面可近似假设为刚性。如图2所示，测点1、2、3均匀布置在横截端面上，测量方向为轴向（向），以轴向振动响应作为角振动测量值。

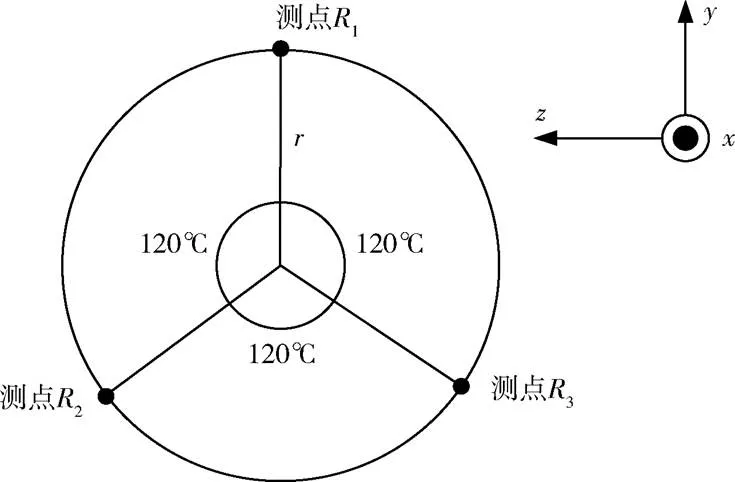
图2 测点R1、R2、R3分布

试验时，由于角振动量无法直接测量，这里假设存在一个虚拟响应点，利用1（向）和端面中心测量点R响应值来计算虚拟角振动量。已知R（向）响应值为(1+2+3)/3，则角振动响应量（转动轴为轴）可表示为1与R之间的线振动量之差除以距离，即[1−(1+2+3)/3]/。本文为便于振动控制条件的计算，角振动响应量A假设以1与R之间的线振动量之差1−(1+2+3)/3来表示（单位为），并与通过外场实测角加速度计算的线振动量进行对比。如无特殊说明，下文提到的角振动量均指换算为线振动量之差的振动量。

经过初步试验测试，获得角振动量A、线振动量4与控制点1和2之间的传递关系；通过外场实测角振动量、线振动量，利用传递关系计算出控制点1和2的振动控制量，从而可实现对角振动和线振动的间接控制。

2 飞行振动环境数据分析

2.1 时域预处理

对飞行振动环境数据的时域分析主要是观测信号有无奇异值、时域趋势项等现象，一般可通过奇异值和趋势项两个方面进行数据处理。

1）奇异值处理

假设所测试的信号极值点幅值服从正态分布，利用6原则进行判断，即在极值点幅值正态分布假设下，如果幅值满足式(1)，则认为幅值以极小的概率出现，是随机过程的小概率事件，可判定其为奇异值。

＞3， (1)

式中：为信号幅值；为幅值均值；为峰值与均值的方差。外场实测信号具有短时非稳态随机特征，一般数据离散度较大。因此，在使用6原则判断信号奇异值的同时，应以振动台可实现的时域峰值进一步判断和修正，并且，通过奇异值修正后的信号在频谱上应与原始实测信号的频谱没有显著差异。

2）趋势项处理

一般采用均值判断方法判断数据趋势项，高信噪比信号时域序列的幅值均值接近于0。理想的振动信号其时域序列幅值均值处处等于0，但由于结构动力学特性的影响，实际情况中，不会出现理想的振动情况，往往振动幅值的均值是有偏离的。在去除趋势项的处理过程中，应注意以分析频率范围或要进行复现的频率范围来度量和判读时域趋势项的存在或是否进行处理。对于本次飞行环境数据，采用经验模态方法（EMD），即非线性、非平稳信号的时域分析方法对趋势项进行了分析和处理。该方法的基本原理是，依据数据内在的特征将信号分解为有限个具有不同特征尺度的本征模函数（IMF），应用高阶IMF分量重组信号来实现趋势项的提取[10]。图3所示为角振动和线振动数据去趋势项处理前后对比结果，其中蓝色虚线表示处理前，红色实线表示处理后。

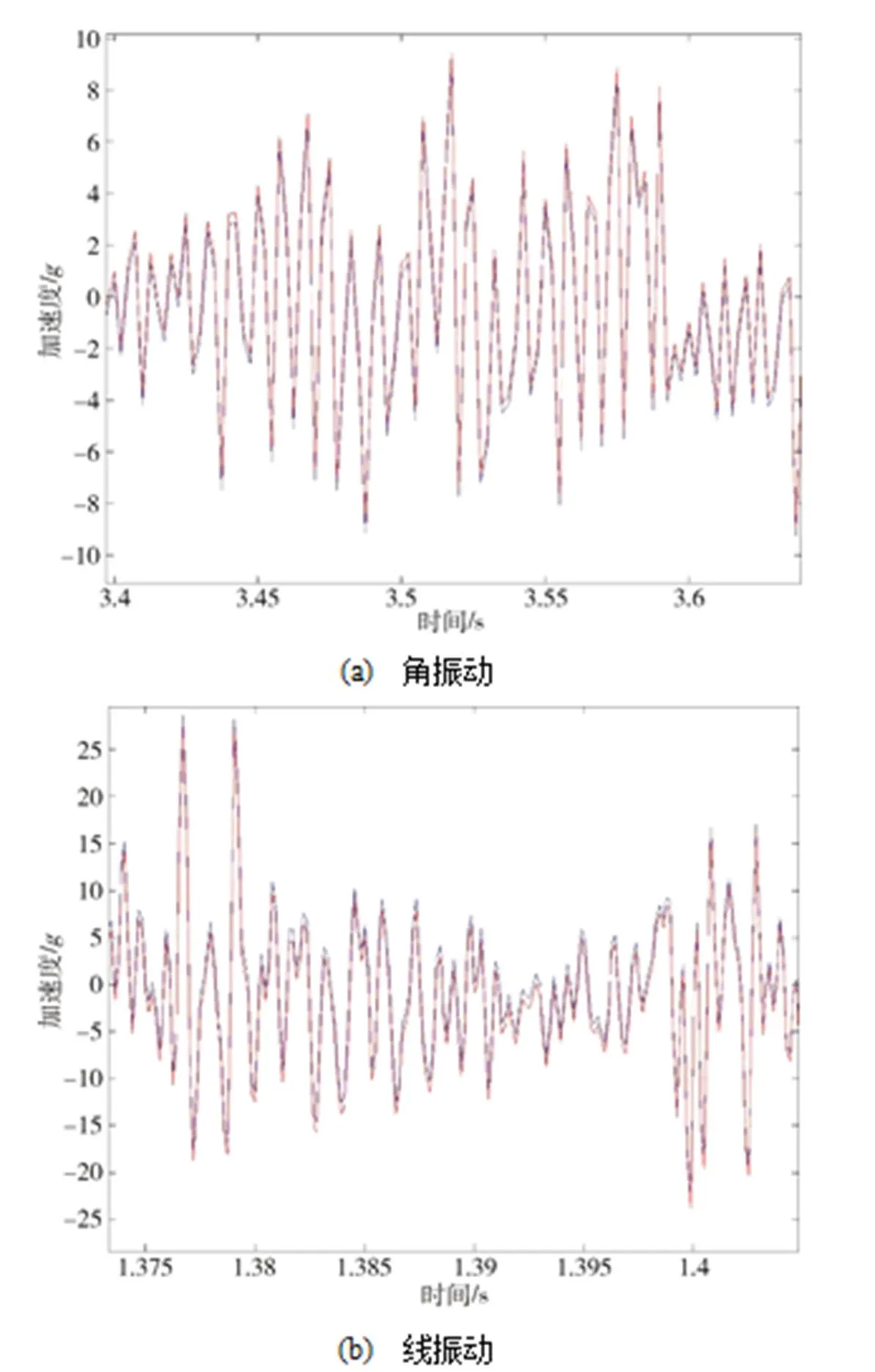
图3 角振动和线振动数据去趋势项处理前后对比

2.2 频域分析

1）重采样过程

在本次线角复合振动试验中，角振动试验主要考核陀螺在角振动环境下的测量精度。外场角振动数据直接通过陀螺仪在实际工况下采集得到，采样频率较低（约为400Hz）；而线振动数据采样频率较高（约为6400Hz）。为在同一振动系统下较为准确地复现线振动和角振动的复合环境，要求两类振动时域数据的采样频率相同，且与振动控制仪的采样频率设置保持一致，这就需要对外场实测的线、角振动数据进行重采样处理。本文分别采用3次分段Hermite函数插值和线性插值的重采样方法对数据进行了处理，重采样频率为5120Hz，线振动数据处理前后局部放大的对比如图4所示。可以看出，Hermite插值的重采样曲线比较平滑，且与原始数据较为接近。

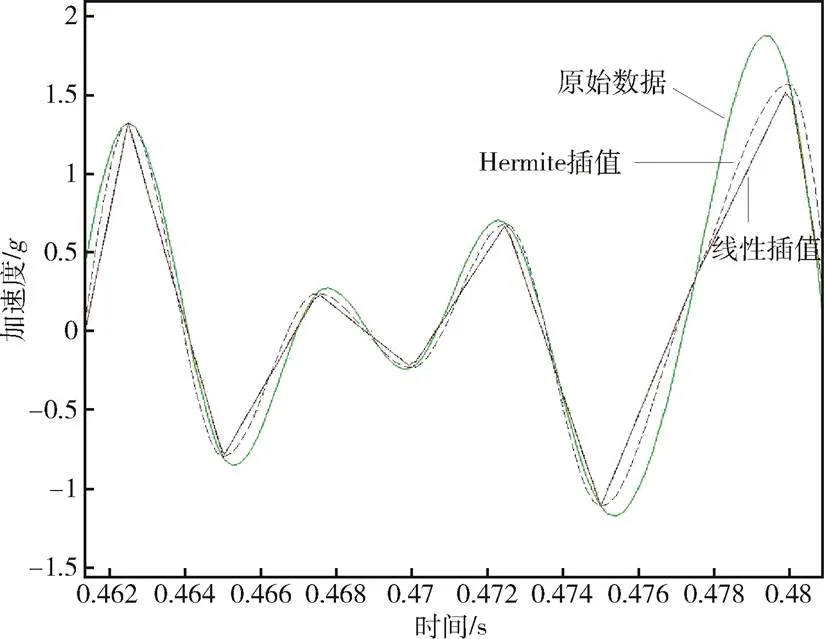
图4 线振动数据重采样处理前后的局部放大对比

2）滤波处理

线振动和角振动的时域波形包含了两类振动的幅值信息及相关关系，其中相关关系不仅表示了振动幅值和相位上的相干特性，还体现了振动形态的变化关系。在开展模拟试验前，需要依据试验系统特性在可实现的频率范围对飞行实测时域数据进行滤波处理，且处理过程不能破坏时域波形之间的相关关系。振动系统的频响函数可表示为

()=()/()， (2)

式中：为输入信号；为响应信号；()为输入和响应的互谱；()为输入的自谱。对()进行加窗处理，可得：

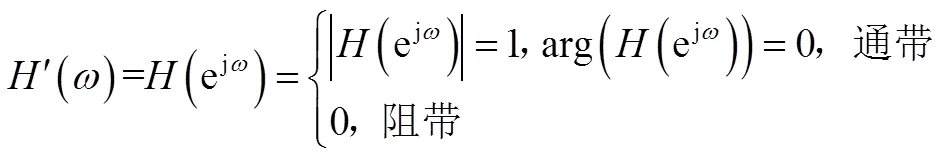
将式(3)代入式(4)，可得滤波后振动数据。

()=′()()， (4)

式中，()和()分别表示待滤波信号和滤波后信号的傅氏谱。

滤波后的数据经过傅里叶逆变换转换为时域数据，其与FFT滤波结果及原始数据的对比如图5所示，可以看出，经过频响函数滤波后数据的时域波形更为平滑，且优于FFT滤波处理结果。

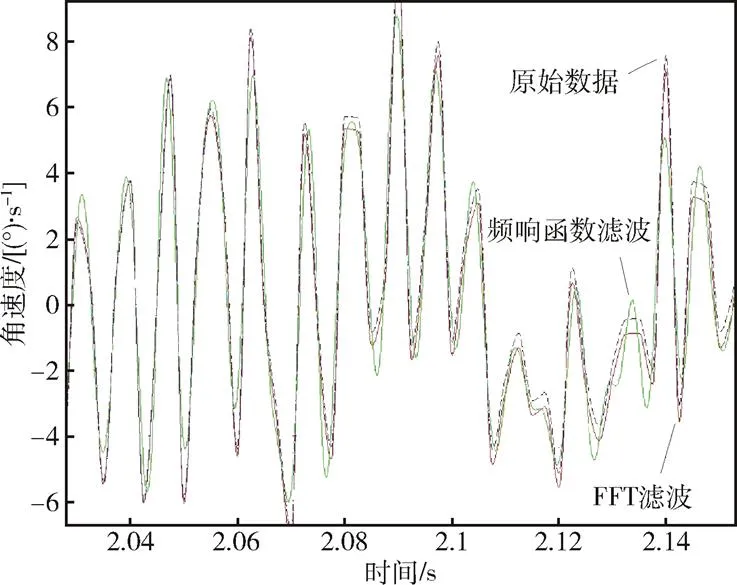
图5 角振动数据滤波处理前后的局部放大对比

2.3 线角振动响应量确定

依据实测数据，角振动量和线振动量在输入频率范围上并不匹配，角振动频率范围为5～200Hz，线振动频率范围为5～1000Hz。如果按线振动（4）和角振动（A）虚拟响应点输入，从经过预处理后的线角振动数据的频谱上看，角振动量在200～1000Hz输入量为0。实际试验时如果为满足角振动量在200～1000Hz范围内输入量为0，将导致振动台的输入量级过大，甚至超出其能力范围。根据试验任务要求，在5～200Hz频率范围内应同时考虑线、角振动响应与实测数据的符合性，而在200～1000Hz频率范围内仅考察线振动与实测数据的符合性，对角振动响应不作考虑。

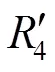
这里的角振动响应均为线振动量之差（单位为）。在200～1000Hz频率范围内，式(5)实际上表示在一个点上度量两个振动台引起的振动响应。由于惯导产品对实际未知的角振动量值不敏感而不考虑，通过式(5)可计算出虚拟响应点的试验控制条件，从而在5～200Hz范围实现对线振动和角振动的控制，以及在200～1000 Hz范围内仅对线振动的控制。虚拟响应点线振动和角振动计算波形如图6所示。

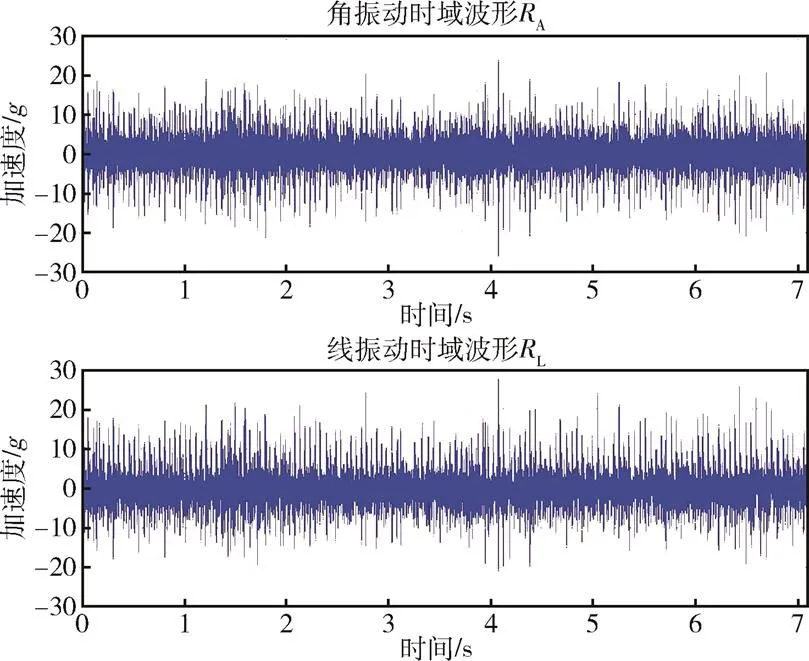
图6 虚拟响应点线振动（RL）和角振动（RA）计算波形

3 模拟再现试验验证

线角复合振动环境模拟再现试验大致流程为：

1）根据试验系统方案计算出线振动测量点和角振动测量点的响应值；

2）通过双台随机振动试验采集控制点和响应测量点的时域波形，计算响应测量点和控制点之间的传递函数；

3）利用传递函数和估算的线振动/角振动量响应值来计算振动控制点的试验控制条件；

4）采用计算的控制条件进行低量级预试验，通过模拟振动控制过程对控制点的试验条件进行修正；

5）应用修正后的控制条件作为线角复合振动试验的输入条件，开展正式验证试验。

3.1 试验控制条件合成

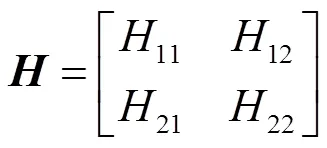
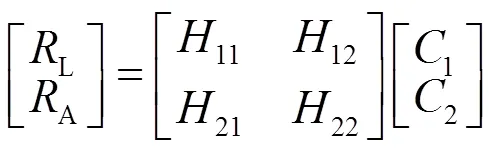
=-1·。 (7)

传函矩阵可能是奇异矩阵且不存在逆阵，定义-1为具有最小范数的Moore-Penrose广义逆，即(-H·)·-H，其中-H为传函矩阵的共轭转置矩阵。根据响应点测试波形计算出试验系统在控制点1和2的试验条件如图7所示。

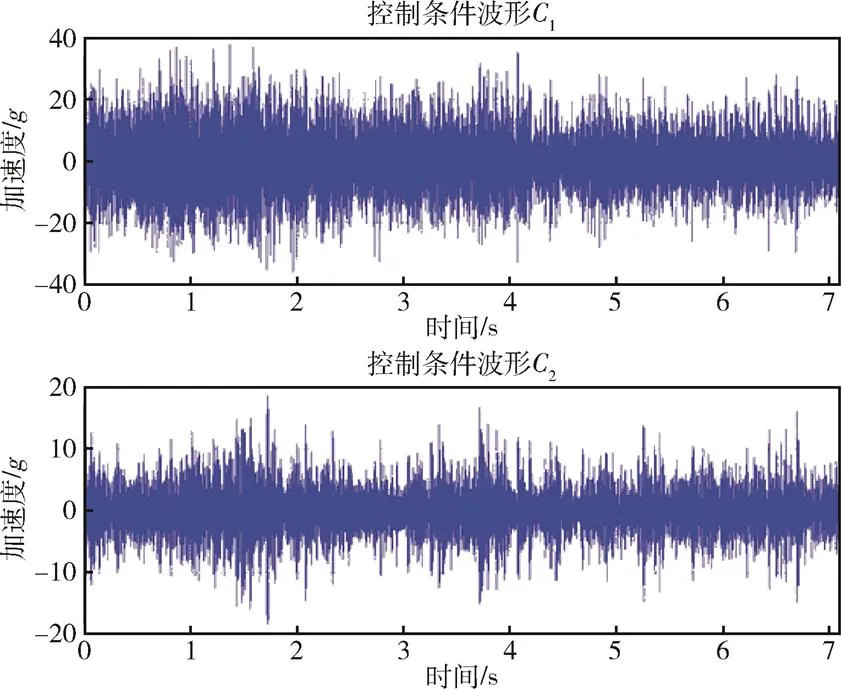
图7 控制点C1和C2初始试验条件波形

3.2 预试验修正

在预试验过程中，图7所示的控制波形只是一个初始条件，在试验量级逐步提高的过程中，应根据线振动与角振动测量值与参考值的误差对控制条件进行不断修正。图8和图9为输入振动量级达到-8dB时，线振动与角振动的参考值（虚线）和响应值（实线）在时域和频域的对比情况。可以看出，线振动及角振动的响应值在时域和频域上与控制条件波形均符合较好，仅在频率100～200Hz之间误差相对较大。这可能是由试验系统模拟边界条件与产品实际使用情况的差异造成的，此时控制点的试验条件波形如图10所示。需要注意的是，试验过程中不适合在整个试验量级上升过程均对控制波形进行修正迭代，这样会使试验次数过多而对试件造成不必要的累积损伤。在合适的试验频度及试验量级范围内，随着试验量级增加，试验控制条件与响应条件的信噪比及传函估计准确性均会进一步提高，由此计算的间接控制点1和2的波形将更为准确。

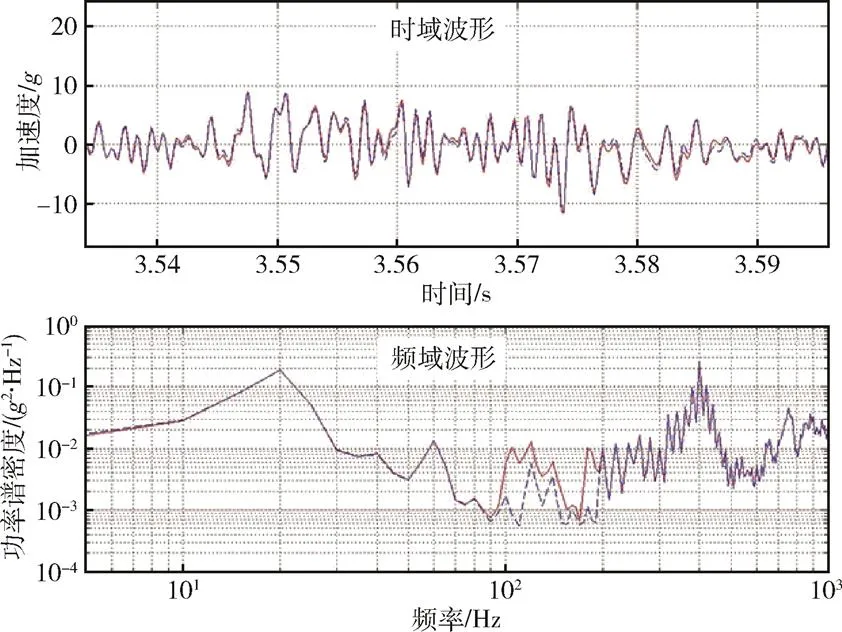
图8 预试验测试的线振动响应波形和控制波形对比

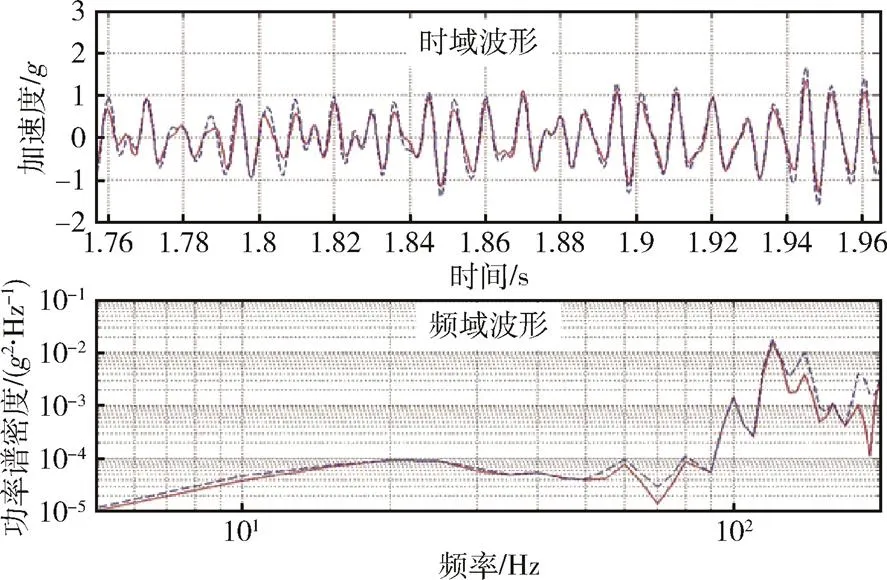
图9 预试验测试的角振动响应波形与控制波形对比

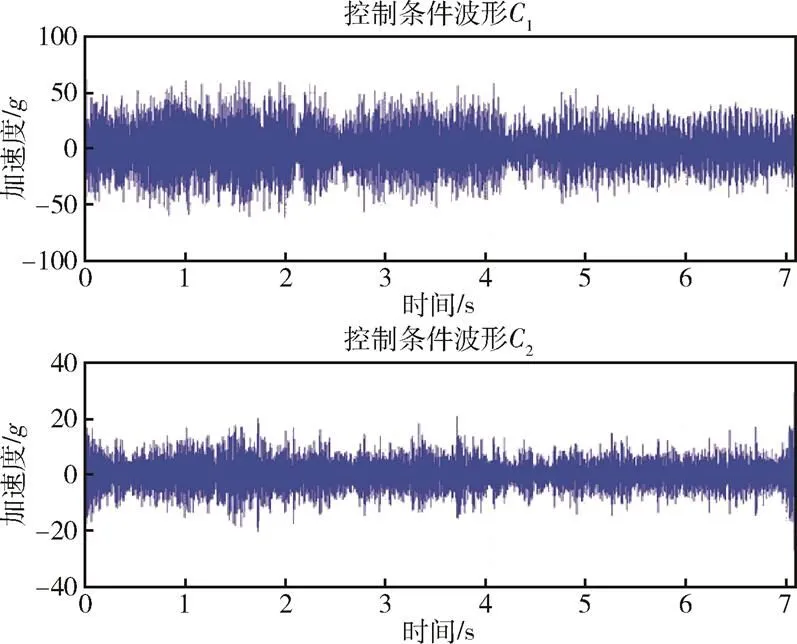
图10 -8dB振动量级下的控制点C1和C2试验条件波形

3.3 试验结果分析

试验测试所得的线振动及角振动的响应波形（实线）与控制波形（虚线）对比结果如图11和图12所示。可以看出，两类振动在时域和频域内的响应波形与控制波形整体符合性较好，最大峰值误差不超过10%，频域误差小于1dB，较好地复现了外场实测飞行环境时域数据的典型特征，达到了预期的试验目的和试验要求。与预试验（-8dB）测试结果相比，在0dB量级线振动时域波形误差变化很小，仅在频域波形100～200Hz范围内误差略有放大，产生误差的原因除了试验系统边界条件模拟差异外，还可能与产品固有频率重叠产生的响应放大有关；角振动时域波形误差变化较小，在低频范围内（＜100Hz）比预试验结果略有放大，且在100～200Hz范围内波形趋势符合性较好，应与计算角振动的两个线振动的误差相减抵消有关。试验现场经过产品设计方的确认后，认为这些线角振动波形复现误差在可接受范围内。

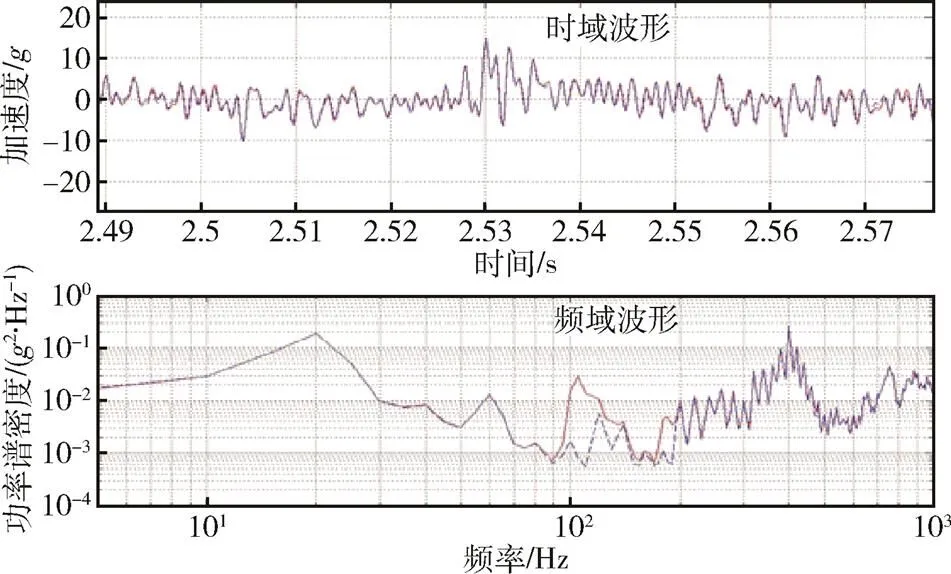
图11 试验测试所得线振动响应波形和控制波形对比

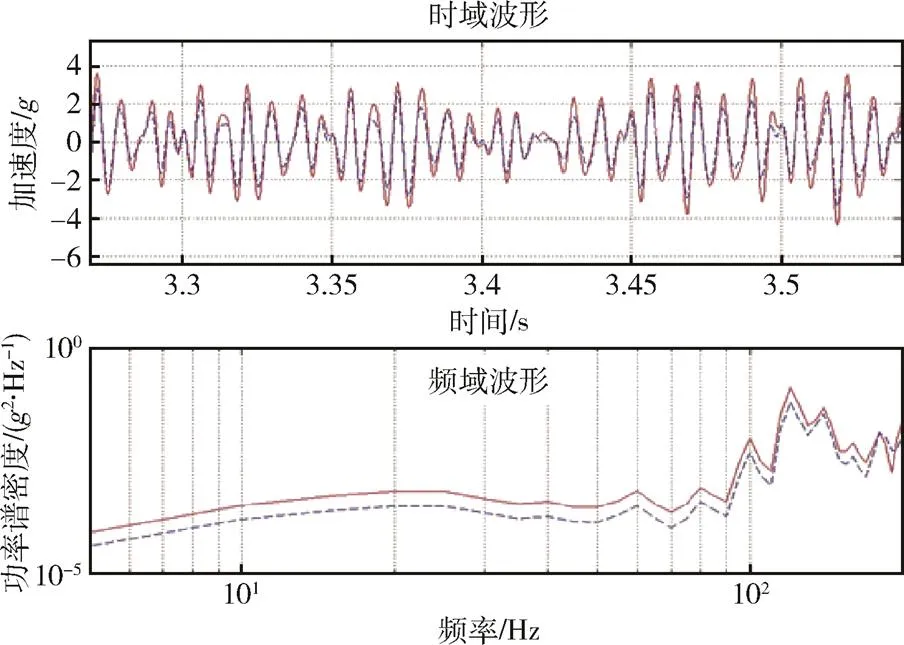
图12 试验测试所得角振动响应波形与控制波形对比

4 结束语

本文以某飞行器系统为研究对象，通过试验系统搭建及试验方法设计，在实验室条件下对外场实测线角复合振动环境进行了模拟再现和试验验证：

1）针对外场实测环境数据，给出了基于奇异值判定及经验模态分析的去除数据奇异值及趋势项的预处理方法；

2）使用自频响函数滤波方法进行数据滤波处理，可以获得较为优良平滑的时域波形曲线，并且满足保持数据相关关系及零相位偏移的处理要求；

3）针对线振动与角振动谱采样频率不一致引起的响应波形计算困难的问题，提出了基于虚拟响

应点进行响应波形计算及试验波形合成的方法，并针对不同响应点采用相应频段进行控制的策略，完成了典型飞行器线角复合振动环境实验室模拟再现的试验任务。

[1] 李晓波, 吴斌, 董程, 等. 捷联惯导减振系统的耦合振动研究[J]. 装备环境工程, 2014, 11(2): 43-49

LI X B, WU B, DONG C, et al. Research on coupled vibration of strapdown INS damping system[J]. Equipment Environmental Engineering, 2014, 11(2): 43-49

[2] 马兴瑞, 韩增尧, 邹元杰, 等. 飞行器力学环境分析与条件设计研究进展[J]. 宇航学报, 2012, 33(1): 1-12

MA X R, HAN Z Y, ZOU Y J, et al. Review and assessment of spacecraft mechanical environment analysis and specification determination[J]. Journal of Astronautics, 2012, 33(1): 1-12

[3] 马兴瑞, 于登云, 韩增尧, 等. 星箭力学环境分析与试验技术研究进展[J]. 宇航学报, 2006, 27(3): 323-331

MA X R, YU D Y, HAN Z Y, et al. Research evolution on the satellite rocket mechanical environment analysis & test technology[J]. Journal of Astronautics, 2006, 27(3): 323-331

[4] 苏华昌, 姜虹, 胡亚冰. 飞行器末制导系统线角振动环境模拟试验技术[J]. 现代防御技术, 2014, 42(3): 48-52

SU H C, JIANG H, HU Y B. Simulation technology of combined linear and angular vibration environment for vehicle terminal guidance system[J]. Modern Defence Technology, 2014, 42(3): 48-52

[5] SMALLWOOD D O, PAEZ T L. A frequency domain method for the generation of partially coherent normal stationary time domain signals[J]. Shock and Vibration, 1993, 1(1): 45-53

[6] UNDERWOOD M A, KELLER T. Recent system developments for multi-actuator vibration control[J]. Sound and Vibration, 2001, 35(10): 16-23

[7] UNDERWOOD M A, KELLER T. Applying coordinate transformations to multi-DOF shaker control[J]. Sound and Vibration, 2006, 40(1): 22-27

[8] 贺旭东, 陈怀海, 申凡, 等. 双振动台随机振动综合控制研究[J]. 振动工程学报, 2006, 19(2): 145-149

HE X D, CHEN H H, SHEN F, et al. Study on dual-shaker random vibration test control[J]. Journal of Vibration Engineering, 2006, 19(2): 145-149

[9] 叶建华, 李传日. 多点随机振动试验控制技术[J]. 系统工程与电子技术, 2008, 30(1): 124-127

YE J H, LI C R. Control technique of multi-exciter random vibration test[J]. Systems Engineering and Electronics, 2008, 30(1): 124-127

[10] 陈冬娣. 基于小波变换与经验模态分解的电机转子振动信号处理方法的研究[D]. 南京: 南京师范大学, 2013: 23-30

（编辑：许京媛）

Reproducing technology of synthetical linear-angular vibration environment for typical aircraft

ZHANG Wenwei, ZHAO Pengfei, PANG Jiazhi, LI Guo

(Aerospace Science & Industry Defense Technology R&T Center, Beijing 100854, China)

To reproduce the combined linear-angular vibration environment during flying for a typical aircraft system in lab, based on the analysis of the measured flying environment data, the control waveform is computed by the dummy response point method. Through building a special testing system, the time-waveform reappearance method is utilized to control the combined linear-angular vibration indirectly. It is shown that the flying environment characteristics of the aircraft could be reproduced below the frequency of 1000Hz, and the simulated testing method could be used to reproduce the outfield vibration environment effectively.

flying environment; synthetical linear-angular vibration; time-domain waveform reappearance; double actuator prompting

V416.5

A

1673-1379(2017)06-0649-07

10.3969/j.issn.1673-1379.2017.06.013

张文伟（1974—），男，硕士学位，高级工程师，研究方向为力学环境及加速试验技术。

赵朋飞（1985—），男，博士学位，高级工程师，研究方向为装备环境工程与可靠性技术；E-mail: 279363896@qq.com。

2017-07-12；

2017-11-26

型号项目支持