星载大型反射面天线主动振动抑制建模分析方法

葛东明，邹元杰，史纪鑫，邓润然



星载大型反射面天线主动振动抑制建模分析方法

葛东明，邹元杰，史纪鑫，邓润然

（北京空间飞行器总体设计部，北京 100094）

为研究抑制星载大型反射面天线的在轨振动，文章给出一种基于压电材料的天线臂主动振动抑制建模分析方法。该方法基于整星刚柔耦合动力学模型，通过将压电材料的应力等价为内力矩，应变等价为位移差分，获得卫星动力学、振动抑制与姿态控制的解析式耦合计算模型，进而预测振动抑制后的天线振动传递特性和响应。以某带大型反射面天线的卫星为例，分别从压电材料布局和计算边界条件角度给出主动振动抑制的时域、频域分析结果，并进行对比。分析结果表明：文章所提出的方法能够实现压电材料在天线臂上的布局优化以及获知天线臂主动振动抑制效果。

卫星；大型反射面天线；在轨振动；主动振动抑制；仿真分析

0 引言

随着卫星在地球探测、射电天文观测、深空通信、能量传输等方面应用的日益广泛，未来星载合成孔径雷达（SAR）将朝着轻量化、经济化、多功能、敏捷快速响应的方向发展[1-3]，因此，星载SAR天线结构将呈现跨度大、质量小、刚度低、阻尼弱等动力学特性，属于典型的大型挠性空间结构，由此带来一系列动力学与控制难题。卫星姿轨控、热应力等导致的机械运动必然会引起大型反射面天线的振动，从而造成其波束指向精度、方位向分辨率、峰值旁瓣比和积分旁瓣比等性能指标的降低，影响航天器任务完成的质量[4-6]。

整星呈现出典型大挠性体特征，是由包含大口径网状天线、多关节大型伸展臂、太阳电池阵与卫星本体组成的大惯量低频刚柔耦合系统。SAR载荷成像时间长，卫星各个环节的振动对成像质量具有不同程度的影响，其中天线臂作为SAR天线支撑和精度保证的关键环节，具有大挠度、低基频的特性，因此天线臂振动对成像的影响至关重要。

针对反射面天线，以往研究工作主要集中在反射面的型面精度控制方面[7-10]，而对于天线的整体振动抑制研究较少，尤其针对基于压电材料的天线臂主动振动抑制建模问题，目前的工程分析方法还缺乏一个顶层的包含卫星动力学、姿态控制与振动抑制的耦合系统模型；分析思路还局限于某一方面的独立分析，如结构动力学分析和简单边界条件下的天线振动分析，多项分析之间缺乏界面划分理论依据，只能给出局部的分析结论[11-12]。例如利用有限元分析软件可以进行天线振动分析，但其多适用于固定边界条件，难以应用在浮动的卫星模型上，且所获得的模型是仿真模型，只能进行响应计算，无法完成基于解析模型的振动机理分析。

因此，本文将压电材料的应力等价为内力矩，其应变等价为位移差分，建立了卫星动力学、振动抑制与姿态控制的解析式耦合计算模型。通过解算此模型，可以获得振动抑制前后的天线振动频率响应和时间响应，便于分析压电材料在天线臂上的布局以及天线臂主动振动抑制效果。

1 动力学-振动抑制-姿态控制耦合建模方法

1.1 整星刚柔耦合动力学建模

带大型可展开网状天线结构的卫星如图1所示。

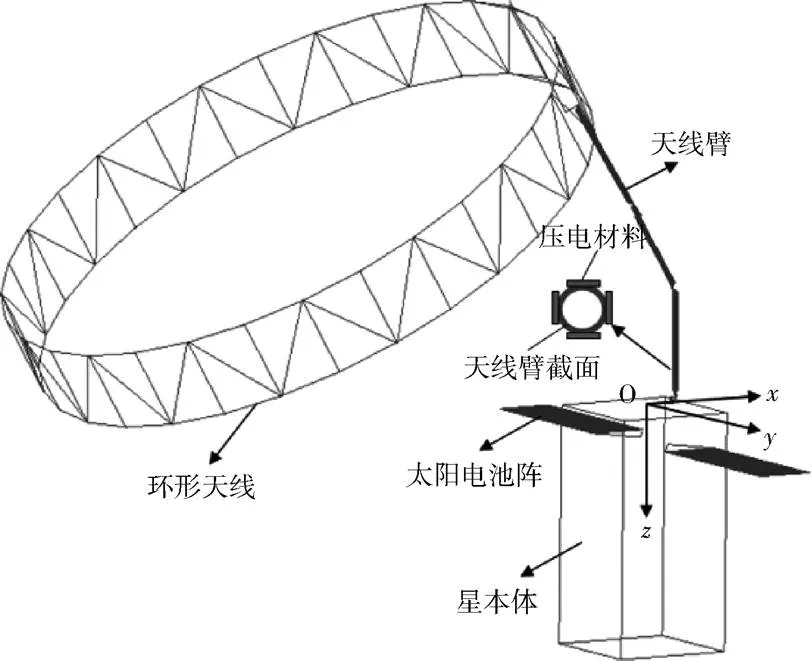
图1 带大型可展开网状天线结构的卫星

为便于振动抑制建模，将带天线臂的大型网状天线作为柔性体考虑，卫星本体作为刚性体考虑，柔性太阳电池阵与本体固定连接。采用柔性动力学建模理论，建立整星刚柔耦合动力学方程：

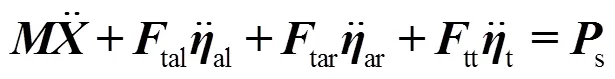
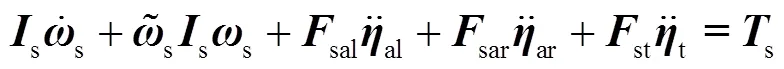
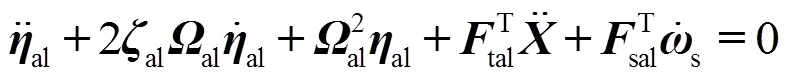
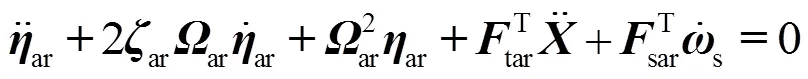
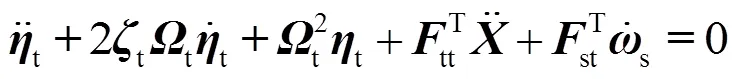
以上各方程中：式(1)为系统质心平动运动方程，式(2)为系统绕质心的转动运动方程，式(3)为+轴太阳电池阵的振动方程，式(4)为-轴太阳电池阵的振动方程，式(5)为天线的振动方程。

1.2 天线臂主动振动抑制建模

由于天线点头模态对波束指向影响最大，所以本文将重点解决点头模态的振动抑制问题。沿天线臂应变最大处的臂杆一周粘贴压电纤维复合材料的应变片，作为传感器测量天线臂应变，并以此作为振动抑制的驱动输入。将作用在天线臂上的驱动效应等效为天线臂应变最大处的臂杆外侧多个作用点的弯矩，添加主动振动控制输入后的天线振动方程(5)变为

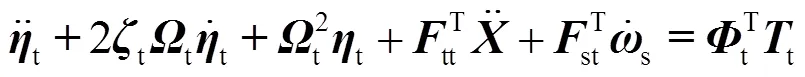
式中：t为作用在天线臂上的各个节点在轴方向的振动控制弯矩；t为振动控制弯矩作用在天线臂上的节点在轴方向的振型。

压电应变传感器测量的是天线臂上粘贴应变片覆盖部分的2个距离最远的节点，在天线臂变形前/后的距离差值。作为控制律的反馈信息，将这2个距离最远的节点定义为反馈节点1和节点2，它们的位置信息为：

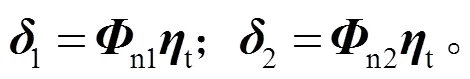
其中：1和2分别为节点1和节点2的位移振动响应；n1和n2分别为节点1和节点2的振型。那么，节点1和节点2的距离变化D为

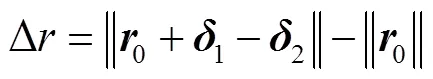
其中：0是节点1和节点2的几何距离，即天线臂变形前两节点间的原有距离；|| ||是取模运算。

设定振动抑制的控制律为速度负反馈，

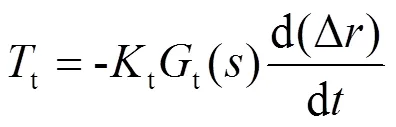
其中：t为图2中天线点头模态的控制弯矩；t为点头模态的控制增益。

对反馈信息进行滤波，只保留点头模态的信息，滤波因子为

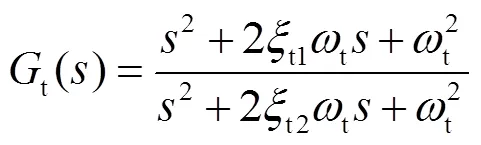
其中：wt为点头模态的振动频率；xt1和xt2为点头模态滤波因子的阻尼比。

1.3 姿态控制建模

设定比例-微分控制律为

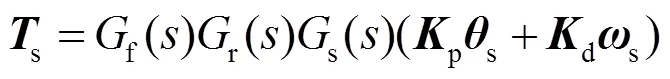
其中：p为比例增益；d为微分增益；s为卫星姿态角；s为控制力矩。卫星姿态角s由陀螺测量得到，控制力矩s由动量轮驱动得到。

陀螺和动量轮的滤波因子分别为：

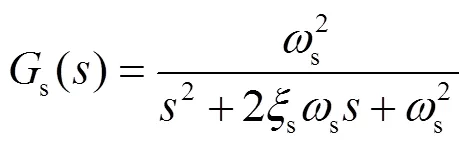
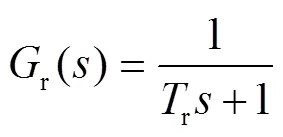
其中：s为陀螺的滤波带宽；s为陀螺滤波因子的阻尼比；r为动量轮机电时间常数。

天线主要振动模态的滤波因子为

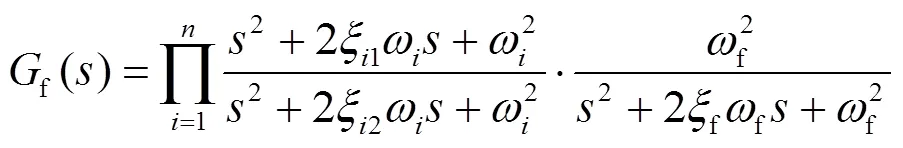
其中：为个待滤波模态的频率，即主要振动模态的频率；1取0.005～0.01；2取21；f为主要振动模态的滤波带宽；f取0.7～1。

1.4 动力学-振动抑制-姿态控制耦合模型

由上述整星动力学模型(1)～(5)、振动抑制模型(6)～(10)和姿态控制模型(11)～(14)，组成如下双闭环的振动抑制与姿态控制耦合模型：

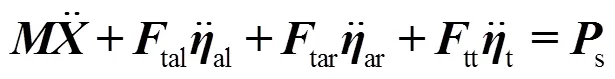
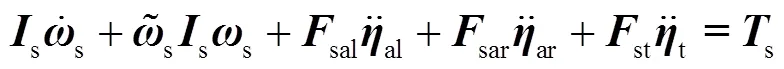
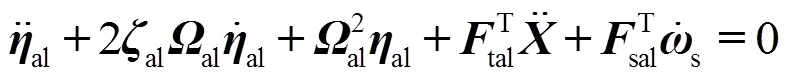
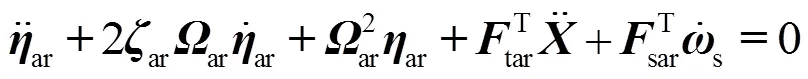
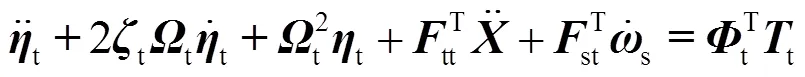
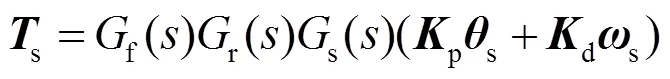
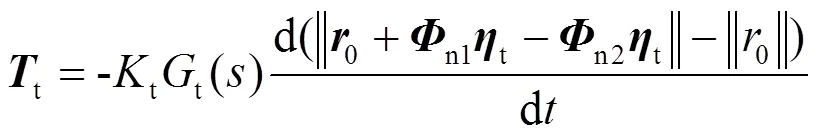
2 仿真分析

以带大型柔性天线的卫星为例，分别进行频域和时域计算，对主动振动抑制方案进行效果分析。首先，通过天线有限元模型分析，天线固支条件下，天线臂根部为点头模态的应变最大处。将压电材料布置在天线臂的根部，分析振动抑制效果。分别建立天线固支和整星浮动条件下的点头模态传递特性，如图3(a)和图3(b)所示。可以看出，天线固支条件下，点头模态传递幅值由0.529降低到0.09。由特征值计算，对应的阻尼比由0.005提高到0.026。然而，在整星浮动条件下，点头模态传递幅值下降不明显，对应的阻尼比由0.0058提高到0.0064。从传递特性上可以看出，在整星浮动条件下，在天线臂根部采取主动振动抑制，对点头模态的振动几乎没有抑制衰减作用。这是由于天线在整星浮动边界条件下振型发生了变化，模态应变能主要分布在天线臂端部，而非天线臂根部，所以，在天线臂根部采集到的变形信息很弱，也就是振动抑制的驱动信号很弱，自然起不到振动抑制的作用。

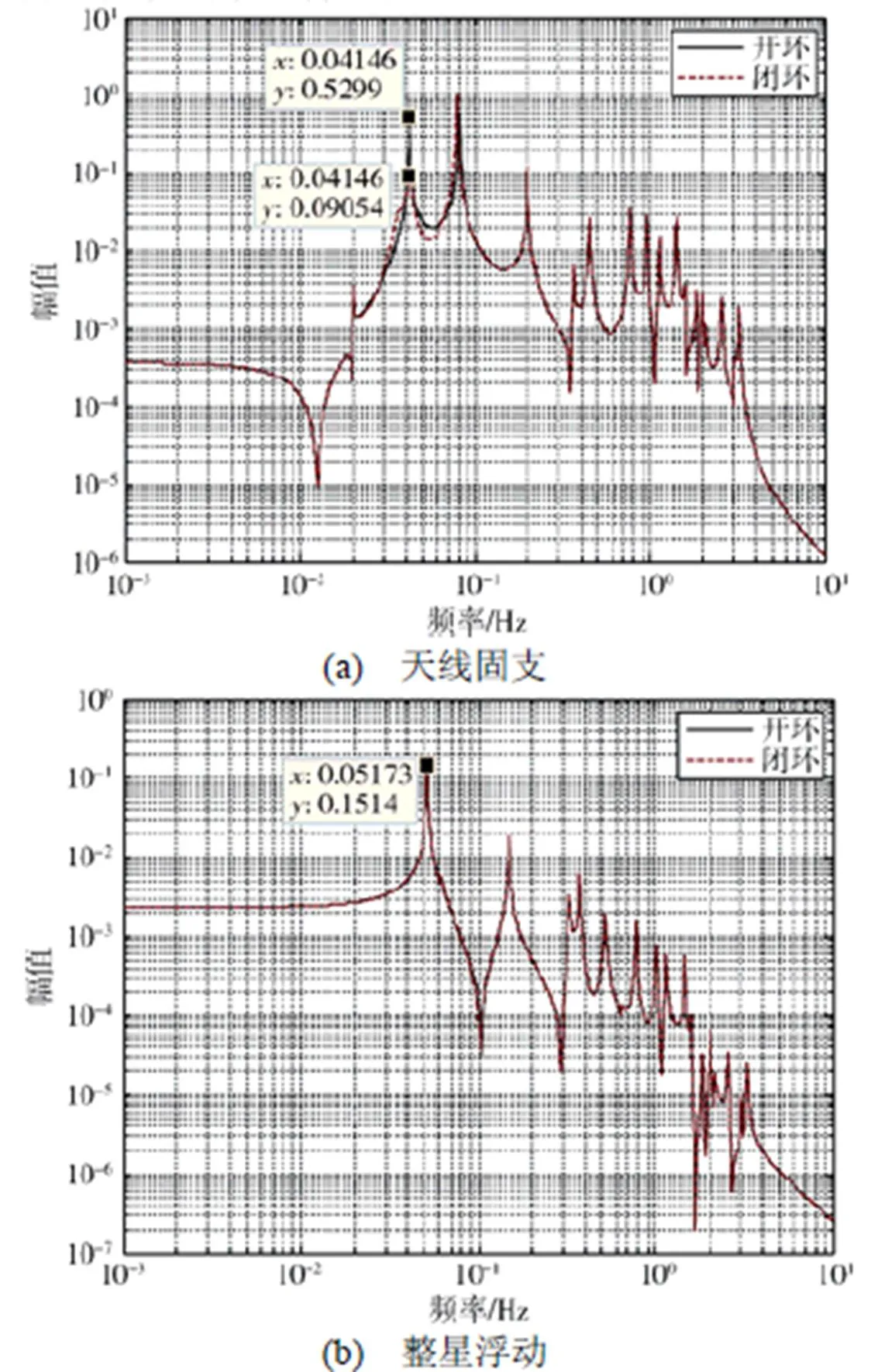
图3 压电材料布置在天线臂根部时的传递特性

重新将压电材料布置在天线最大应变处，即天线臂端部，再通过计算天线的振动传递，得到天线点头模态的频率响应（见图4）。可以看出，点头模态传递幅值由0.163降低到0.06，对应的阻尼比由0.0058提高到0.0175，振动抑制效果明显增强。将压电材料布置在天线臂的端部，在本体施加激励，通过计算天线的振动时间响应，获得天线远端点的振动位移响应（见图5）。通过阻尼比计算，获得振动抑制前的自由振动阻尼比为0.009，施加振动抑制后的阻尼比为0.02，提高了122%，与频率响应分析结果一致，振动抑制效果明显增强。

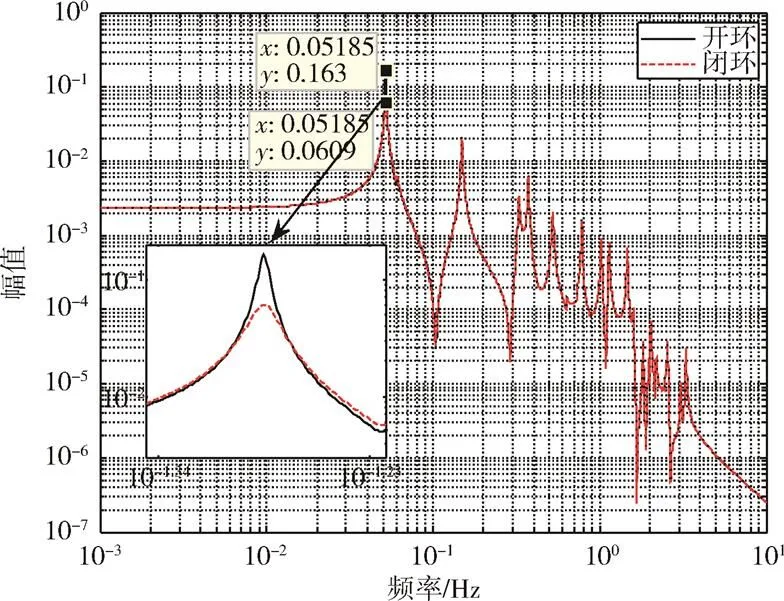
图4 压电材料布置在天线臂端部时的整星传递特性

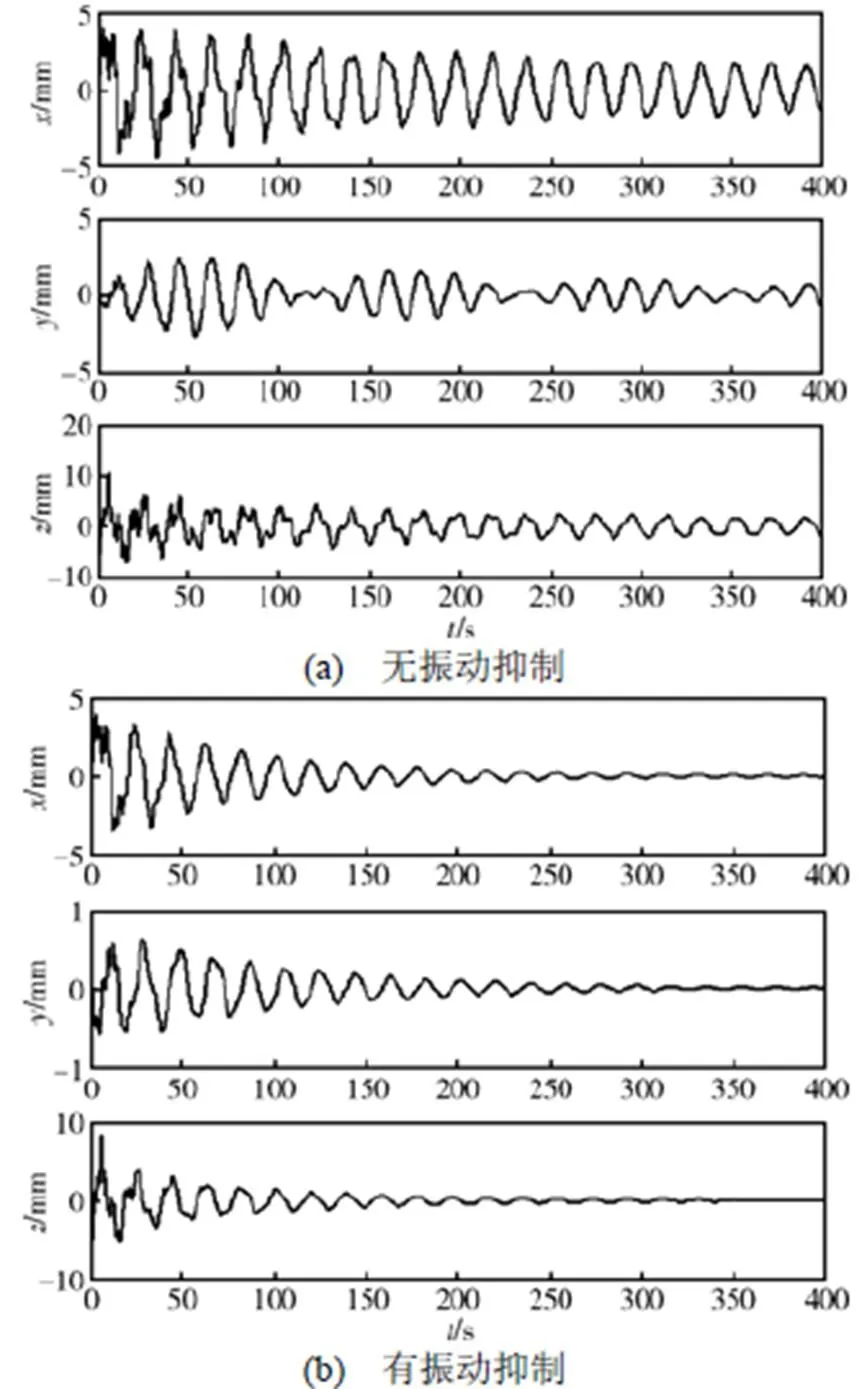
图5 压电材料布置在天线臂端部的天线远端点振动位移响应

3 结论

本文给出了一种基于压电材料的天线臂主动振动抑制建模分析方法，针对某星载大型反射面天线模型，将卫星动力学、振动抑制与姿态控制集成为解析式耦合计算模型，分别从压电材料布局和计算边界条件角度，计算并分析了振动抑制前后的天线振动传递特性和响应。分析结果表明：本文提出的方法能够实现压电材料在天线臂上的布局优化，获知天线臂主动振动抑制效果。相比于传统的固定边界条件有限元分析方法，本方法更适用于卫星真实的在轨浮动状态，且可以实现主动振动抑制的闭环传递特性和响应分析，建模方法简捷实用，建模周期短，便于工程应用。

[1] 段宝岩. 大型空间可展开天线的研究现状与发展趋势[J].电子机械工程, 2017, 33(1): 1-14

DUAN B Y. The state-of-the-art and development trend of large space-borne deployable antenna[J]. Electro- Mechanical Engineering, 2017, 33(1): 1-14

[2] 宗亚雳, 王伟, 王从思, 等. 型面周期性误差对环形桁架可展开天线电性能的影响及其消除方法[J]. 电子学报, 2014, 42(5): 963-970

ZONG Y L, WANG W, WANG C S, et al. Effects of periodic geometric error of AstroMesh reflector surface on radiation pattern and its elimination method[J]. Acta Electronica Sinica, 2014, 42(5): 963-970

[3] 王从思, 保宏, 仇原鹰, 等. 星载智能天线结构的机电热耦合优化分析[J]. 电波科学学报, 2008, 23(5): 991-996

WANG C S, BAO H, QIU Y Y, et al. Coupled structural- electromagnetic-thermal optimization design and

analysis of intelligent[J]. Chinese Journal of Radio Science, 2008, 23(5): 991-996

[4] THOMSON M W．AstroMesh deployable reflectors for Ku-and Ka-band commercial satellites[C]//20thAIAA International Communication Satellite Systems Conference and Exhibit, 2002

[5] MIYASAKA A, HOMMA M, TSUJIGATA A, et al. Design and ground verification of large deployable reflector[C]//42ndAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamic and Materials Conference and Exhibit, 2001

[6] MEGURO A, HARADA S, WATANABE M. Key technologies for high-accuracy large mesh antenna reflectors[J]. Acta Astronautica, 2003(53): 899-908

[7] HILL J, WANG K W, FANG H. Advances of surface control methodologies for flexible space reflectors[J]. Journal of Spacecraft and Rockets, 2013, 50(4): 816-828

[8] TANAKA H, NATORI M C. Shape control of space antennas consisting of cable networks[J]. Acta Astronautica, 2004(55): 519-527

[9] WANG Z W, LI T, CAO Y Y. Active shape adjustment of cable net structures with PZT actuators[J]. Aerospace Science and Technology, 2013, 26(1): 160-168

[10] XIE Y M, SHI H, ALLEYNE A, et al. Feedback shape control for deployable mesh reflectors using gain scheduling method[J]. Acta Astronautica, 2016(121): 241-255

[11] SHI H, YANG B, THOMSON M, et al. A nonlinear dynamic model and free vibration analysis of deployable mesh reflectors[C]//52ndAIAA/ASME/ASCE/AHS/ASC Structural Dynamic and Materials Conference and Exhibit, 2011

[12] 刘洋, 张卫忠, 孟秀云. 网状天线反射器动力学建模及模态分析[C]//2015全国仿真技术学术会议. 南京, 2015

（编辑：张艳艳）

Active vibration suppression modeling and analysis for large satellite reflector antennas

GE Dongming, ZOU Yuanjie, SHI Jixin, DENG Runran

(Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

This paper concerns the active vibration suppression modeling and analysis for the large satellite reflector antenna arm of piezoelectric material. The internal moment and the displacement difference are considered in the place of the stress and the strain of the piezoelectric material, respectively. By building an explicit coupling model based on the rigid-flexible coupling satellite model as well as the vibration suppression and attitude control system, the method can be used to predict the transfer characteristics and the vibration responses of the antenna structure. For a large satellite reflector antenna, the results in the time/frequency domains are analyzed with respect to the piezoelectric material layout and the computing boundary condition, respectively. The analysis results show that the presented method can be used to determine a reasonable layout of the piezoelectric material on the antenna arm, and for the performance analysis of the active vibration suppression.

satellite; large reflector antenna; in-orbit vibration; active vibration suppression; simulation analysis

V443+.4; V414.3+.3

A

1673-1379(2017)06-0593-05

10.3969/j.issn.1673-1379.2017.06.004

葛东明（1982—），男，博士学位，高级工程师，从事航天器动力学与控制工作。E-mail: gedm1982@163.com。

2017-09-21；

2017-11-23