基于随机振动响应的结构非线性参数识别

张鹏飞，付玮，苏华昌，吴家驹



基于随机振动响应的结构非线性参数识别

张鹏飞，付玮，苏华昌，吴家驹

（北京强度环境研究所，北京 100076）

复合材料结构呈现出典型的量级非线性特征，非线性刚度的研究是结构设计和分析的基础。结构使用环境多数存在随机振动载荷，在更接近真实使用环境下对非线性参数的识别结果更加适用。文章提出了基于随机减量法和连续小波变换的非线性参数识别方法，设计了基于随机振动响应的非线性刚度识别程序；通过立方刚度单自由度非线性系统算例，验证了识别方法和程序；并通过试验研究了典型复合材料结构的量级非线性特征。结果表明，基于随机减量法和连续小波变换的非线性参数识别方法具有较好的识别精度，多自由度系统不同谐振阶次的非线性特性存在差别。研究结论对于随机振动环境下结构非线性参数识别和建模具有一定的参考价值。

非线性刚度；随机减量法；连续小波变换；计算分析；试验验证

0 引言

结构动力学分析与试验相关性研究的目的是要通过试验结果修正数学模型，然后用修正后的数学模型计算复杂振动载荷下的响应。这对于线性系统来说困难不大。然而，航天器结构实际上呈现出某种程度的非线性品质[1-2]。非线性可能起因于结构（连接处的松动和摩擦）、材料性质（阻尼、刚度）及某些部件（减振器、飞船支撑机构）等[3]。但目前可用的多数分析过程都是基于线性理论的，如将其直接应用于非线性系统的分析，则可能引入较大的误差。因此，通过试验识别结构非线性特征是一个需要解决的问题。

在结构动力学领域，可以通过观测不同激励水平作用下系统的共振频率及峰值的变化来判断系统是否具有非线性因素。图1是某结构件振动传递特性随振动量级变化的实测曲线，其振动传递率随激励量级的变化很大，系统的增益和谐振频率随激励量级下降，这表明系统呈现出含有渐软刚度的非线性特征。对于刚度非线性系统，刚度将随振动频率和幅值变化，线性系统对刚度的识别方法不再适用。

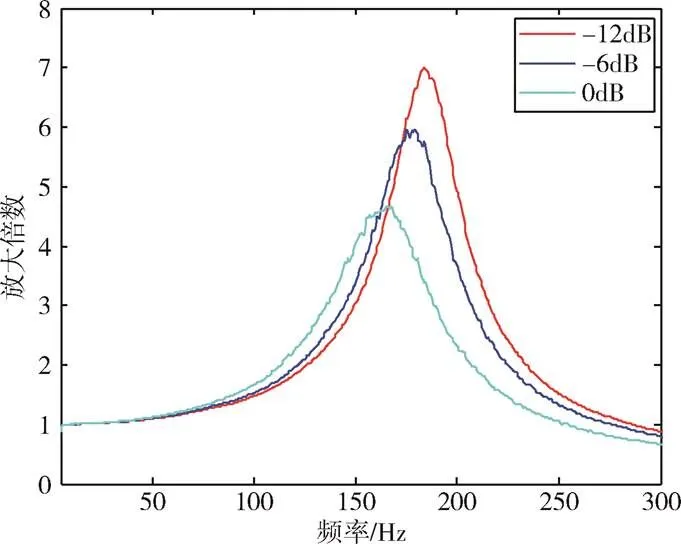
图1 振动传递率量级非线性

目前对于结构非线性刚度的识别，多是基于静刚度或正弦定频试验的刚度曲线，使用最小二乘法进行拟合[4-5]；或者基于冲击响应，使用瞬态信号分析方法进行识别[6]。然而结构使用环境多数存在随机振动载荷，因此在更接近真实环境下的非线性参数识别结果更加适用，而且可以将随机振动环境试验测量结果直接应用于结构非线性参数识别。

本文基于非线性系统的随机振动响应，研究非线性刚度识别方法。首先研究随机减量法在非线性系统中的适用性，在此基础上提出基于随机减量法和连续小波变换的非线性刚度识别方法；然后设计单自由度算例对该方法进行验证；最后用典型复合材料板试件的试验数据进行多自由度系统的非线性参数识别，讨论不同阶谐振频率对应的非线性特性之间的差别。

1 基于随机减量法和连续小波变换的结构非线性特性识别方法

1.1 随机减量法

随机减量法是在结构的随机响应信号中提取出该结构的自由振动响应的一种处理方法。该方法主要是利用平稳随机过程中振动信号均值为0的性质，辨别其中的确定性振动信号和随机振动信号，将确定性振动信号中从中分离出来[7-8]。

在任意激励作用下，单自由度系统的受迫振动响应表示为

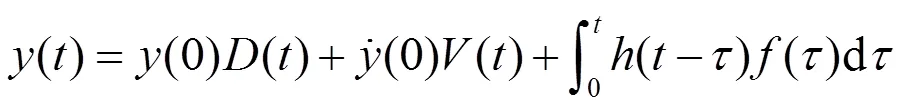
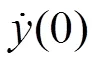
取一固定的振幅去截断随机振动响应，得到一系列不同的交点时刻，对于从t时刻开始的响应(-t)可以看作3部分响应的线性叠加：第一部分为t时刻初始位移引起的自由振动响应；第二部分为t时刻初始速度引起的自由振动响应；第三部分为从t时刻开始的外部激励引起的强迫振动响应。即：

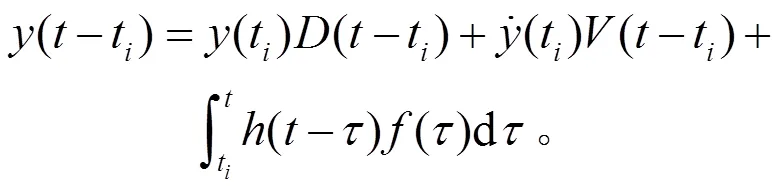
将各子样的起始时刻移至坐标原点，即t=0，可以得到

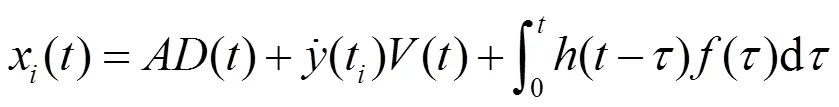
对()取数学期望得到

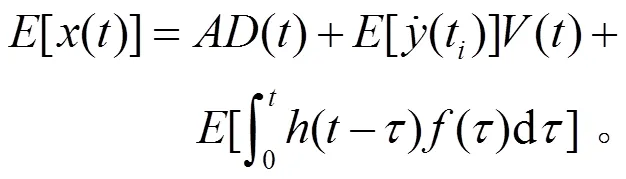
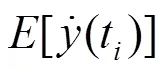
[()]=()。 (5)

上式表明，子样x()的期望是初始位移为、初始速度为0的自由振动响应。实际测量时，因样本长度有限，数学期望以随机减量特征函数()代替，

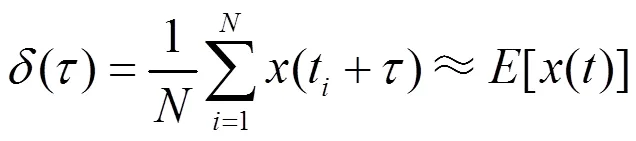
上述分析表明，一个受平稳随机激励的系统，它的响应经过多段平均，随机响应的平均结果为0，剩下确定性响应。最后得到的随机减量特征便是与外载荷无关的自由衰减响应。

1.2 随机减量法在非线性系统中的应用

随机减量法在线性系统中有着广泛的应用，但缺少在非线性系统中应用的研究和案例。下面设计典型的刚度非线性模型，用数值计算的方法验证随机减量法在非线性系统中的适用性。

考虑三次刚度（立方刚度）的非线性，这种情况下，力-位移关系具有以下形式：

s()=+33。 (7)

其中：s为减振器的弹性力；为减振器位移；、3为减振器自身特性确定的常数。对于一般机械结构，3＜0，刚度随位移的增加而逐渐减小，也称为具有软特性。具有立方刚度的单自由度系统强迫振动微分方程为

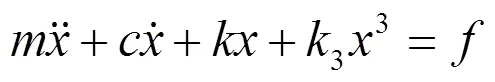
其中，和分别为单自由度系统的质量和阻尼。使用龙格-库塔数字积分方法求解上述运动微分方程的数值解。在MATLAB中生成3组不同大小方均根值的高斯随机振动信号作为力输入，求解对应的响应。对于每一组随机振动响应，分别使用随机减量法求解自由衰减曲线，其中参考值选为随机响应信号的方均根值。同时，按照随机响应信号的方均根值作为微分方程的初值，计算非线性系统在阶跃信号下的自由衰减曲线。将两种方法计算结果进行对比。

图2所示是3种不同的初始量级下，随机减量法和直接积分计算得到的单自由度非线性系统自由衰减响应。对比可见，随机减量法计算结果在开始的几个周期内和直接积分的结果一致性很好，但随着时间增加，随机减量法的偏差逐渐增大。表1给出了初始位移0.0170m情况下，前5个周期内幅值和频率的计算对比结果，相对偏差均在5%之内。

计算结果表明，对于考虑刚度非线性的单自由度系统，随机减量法计算得到的自由衰减曲线在靠前的几个周期内具有较高的精度。

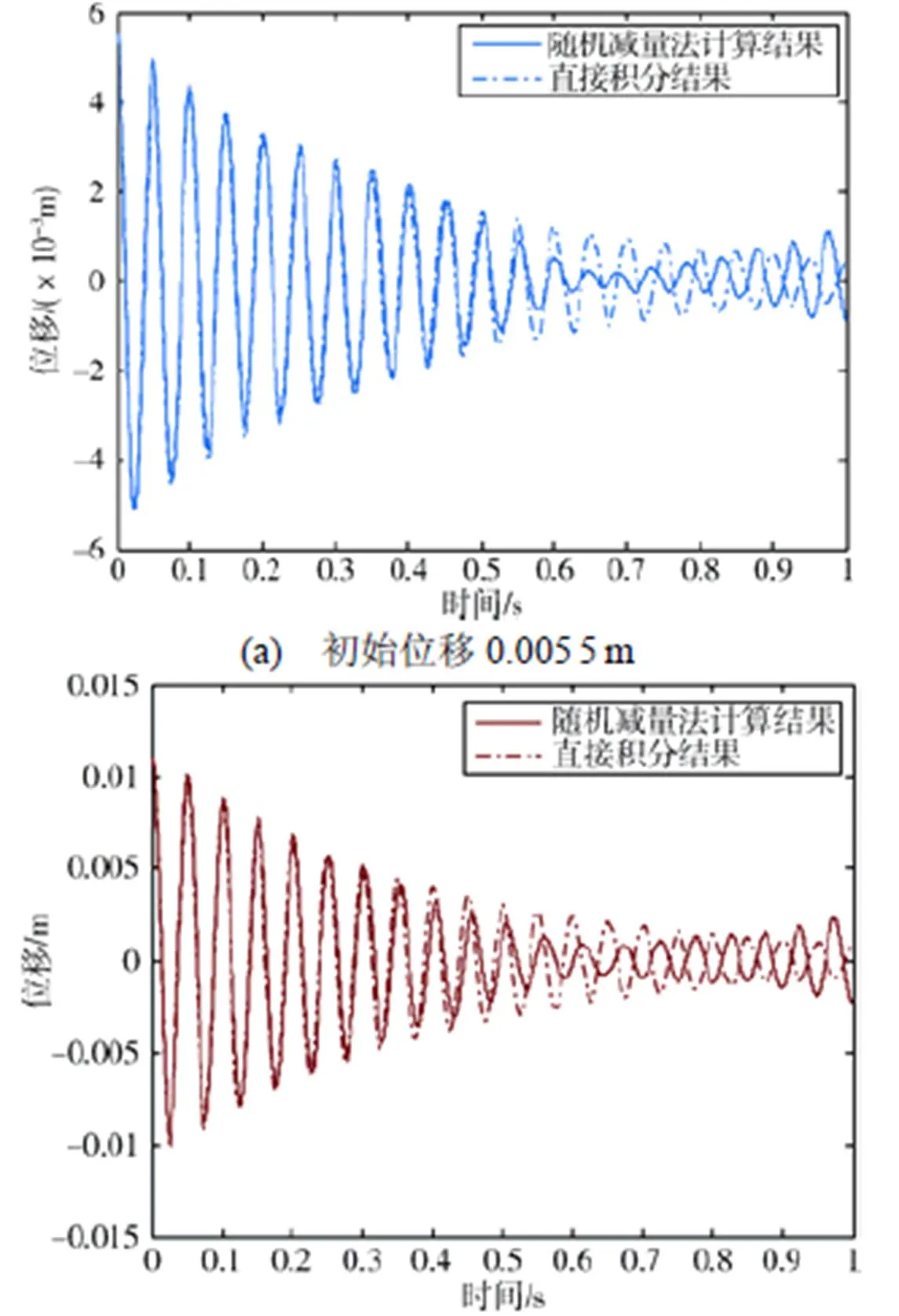
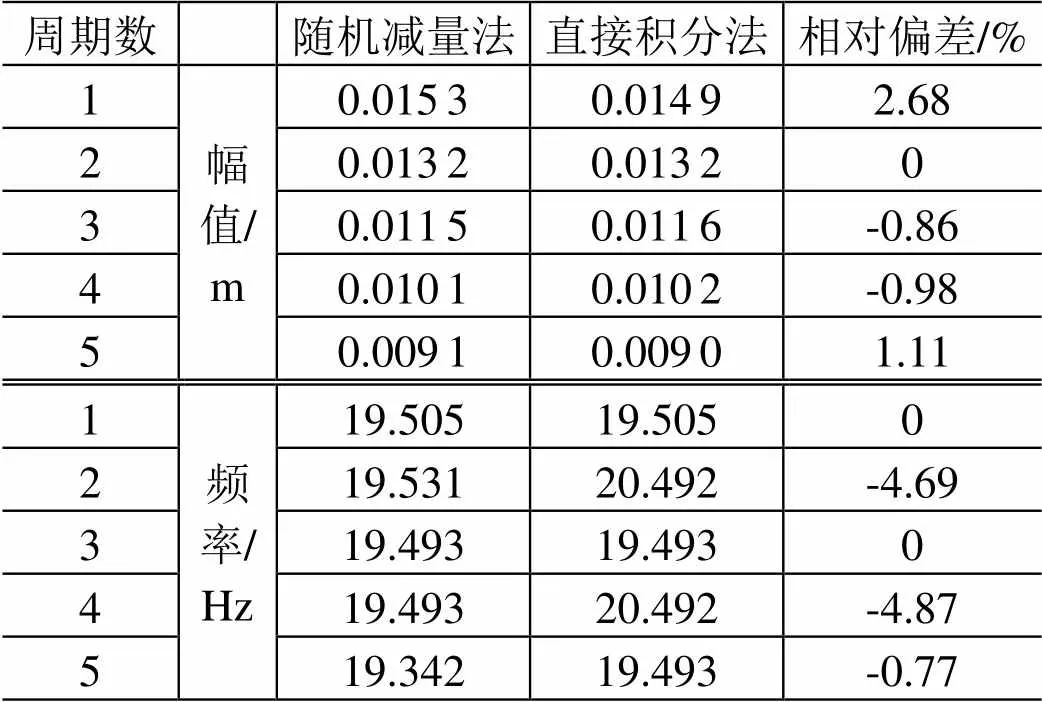
表1 随机减量法与直接积分结果对比

1.3 小波变换在非线性参数识别中的应用

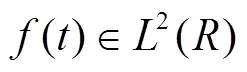
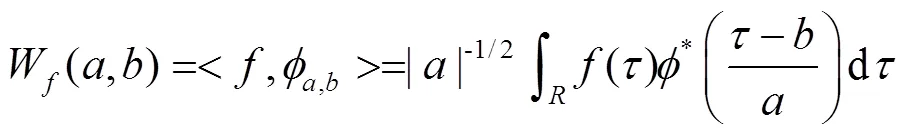
小波尺度谱可定义为

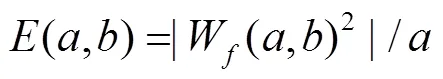
在某一时刻小波系数的最大值满足

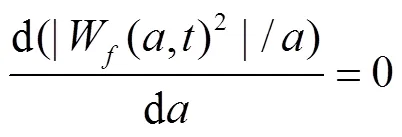
当取不同的值，所有的最大值点的集合形成了小波脊线。通过求出时频面上每一时刻小波系数模极大值，来获得信号中各分量对应的小波脊线，进而获得不同频率信号分量的时频特性。

1.4 随机振动环境中结构非线性特性识别方法

随机减量法与小波变换的结合在结构模态识别中有过成功的应用。Lardies等采用随机减量法将一个多自由度系统的环境激励响应转换为脉冲激励响应，然后利用小波变换估算了系统的固有频率和阻尼比[10]。在非线性系统中，正如1.2节的讨论，随机减量法计算得到的自由衰减曲线只有在靠前的几个周期内具有较高的精度。利用这一特性，提出了一种细分随机减量参考值的数据分析方法。

对于单自由度系统，非线性特性分析方法如下：1）利用随机减量法，在随机振动响应中提取出给定幅值下的自由衰减信号；2）随机减量法的参考幅值选为随机响应信号的方均根值，即ref(1)=RMS()，为随机响应信号；3）改变参考幅值，例如选取20个参考幅值，ref()=ref(1)×(1-× 0.02)，=1,2,…,20；4）对应不同参考幅值下计算得到的自由衰减曲线，分别进行连续小波变换，使用Motlet连续小波作为小波基；5）分别选取不同参考幅值下小波脊线的起始部分，将对应的频率求平均，作为该参考幅值下结构的谐振频率；6）将不同参考幅值对应的频率进行综合，得到频率-幅值曲线，按照该曲线分析结构的非线性特性。

实际结构一般都是多自由度系统，对于随机振动环境中的多自由度系统，非线性特性分析方法如下：1）利用随机减量法，在随机振动响应中提取出给定幅值下的自由衰减信号，该信号包含结构的多个频率成分；2）对自由衰减信号进行连续小波分析，识别出结构的主要频率成分，并提取出不同频率对应的小波脊线幅值；3）对应某一阶频率，按照前述单自由度的分析方法，改变随机减量法的参考幅值，得到该阶频率对应的频率-幅值曲线。

2 数值算例

具有立方刚度的单自由度系统自由衰减微分方程为

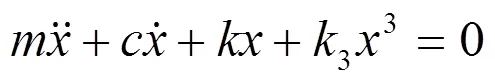
取阻尼比=0.02，谐振频率=20Hz，非线性刚度3/=-64。在MATLAB中生成一组高斯随机信号作为输入信号，使用龙格-库塔方法求解微分方程，得到单自由度系统的随机振动响应()。

以计算得到的随机振动响应()为基础，利用随机减量法，计算给定幅值下的自由衰减信号。随机减量法的参考幅值ref(1)选为随机响应信号的方均根值，即ref(1)=RMS[()]，共选取20个参考幅值，ref()=ref(1)×(1-×0.03)，=1,2,…,20。

对不同参考幅值下计算得到的自由衰减曲线进行连续小波变换。分别选取不同参考幅值下小波脊线的起始部分，将对应的频率求平均，作为该参考幅值下结构的谐振频率。将不同参考幅值对应的频率进行综合，得到频率-幅值曲线如图3所示。

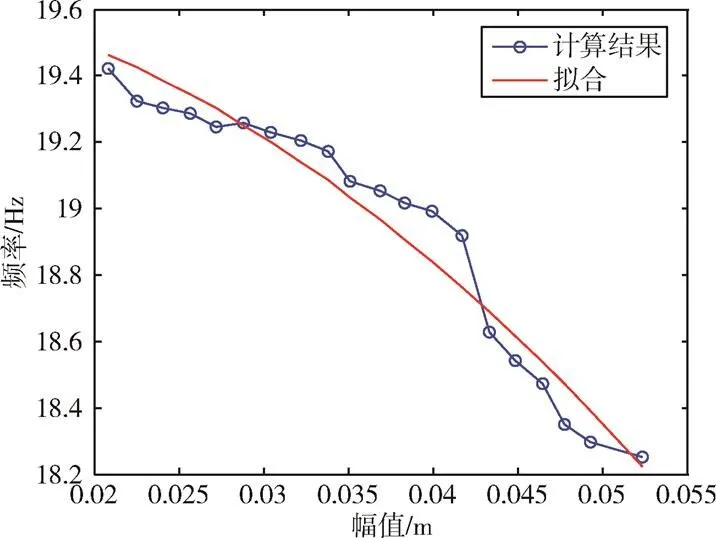
图3 单自由度系统频率-幅值曲线

对于立方刚度非线性系统，频率和振动幅值间存在如下关系[11]：

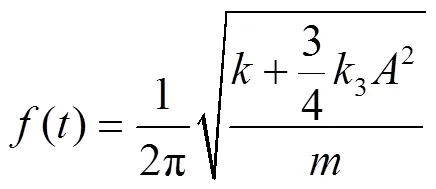
根据式(13)和图3，拟合求解得到3/=-73。与实际值-64相比，相对偏差为14.06%。

3 实例分析

以某异形复合材料板为例，进一步验证随机振动环境中结构非线性特性分析的方法。

异形板随机振动试验采用多台并激的方法施加振动。4个200kg推力振动台布置在异形板的方向，台面向上。振动台通过激振杆与激振块连接，激振块螺接在振动工装上。振动控制点位于激振杆与振动工装连接点附近，每个振动台对应1个控制点。试验采用加速度响应控制的方法，对4个振动台进行谱矩阵控制。加载环境为向平动，4个振动台相干系数设置为1，相位设置为0。图4为异形板随机振动试验系统示意图。

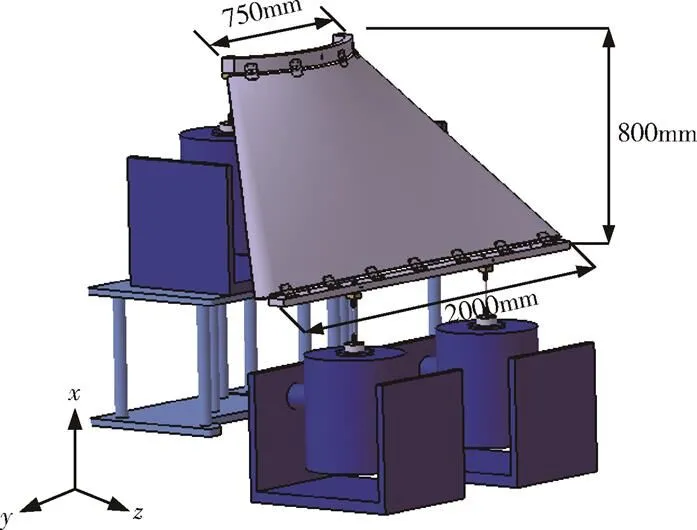
图4 梯形复合材料板x方向振动试验示意

以布置在异形板中部的加速度测点为例进行数据分析。图5是随机振动加载谱形，在20～300Hz之间基本是平直谱形，加载高斯平稳随机振动。图6是异形板上加速度测点的时域响应。

对图6中的随机振动响应信号进行随机减量计算，用该信号的方均根值作为起始幅值，对该信号进行截取、叠加、平均，叠加的样本数约为1000，时间长0.2s。叠加后的自由衰减信号见图7。对该段自由衰减信号进行连续小波变换，得到的频谱等高线见图8。图8中的2条脊线展示了信号中2个主要频率成分随时间的变化，这2个主要频率在48Hz附近和146Hz附近。

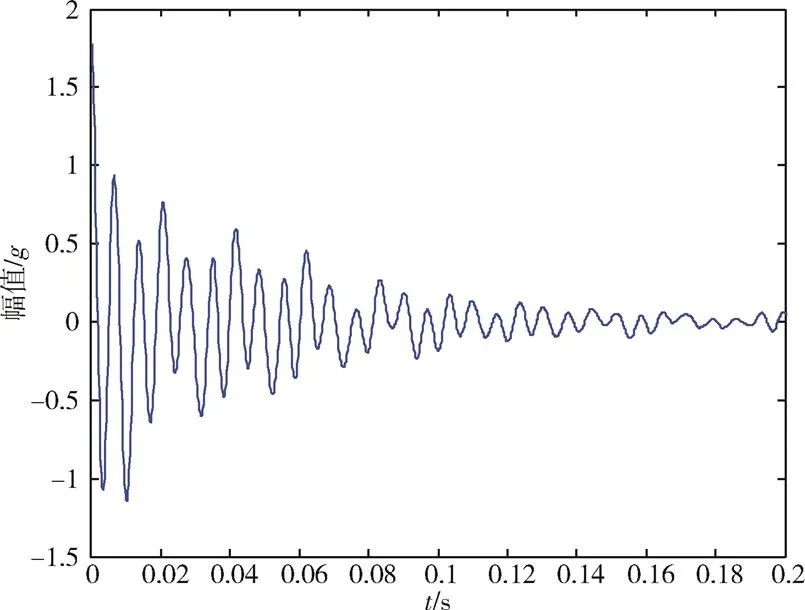
图7 随机减量计算后的自由衰减信号

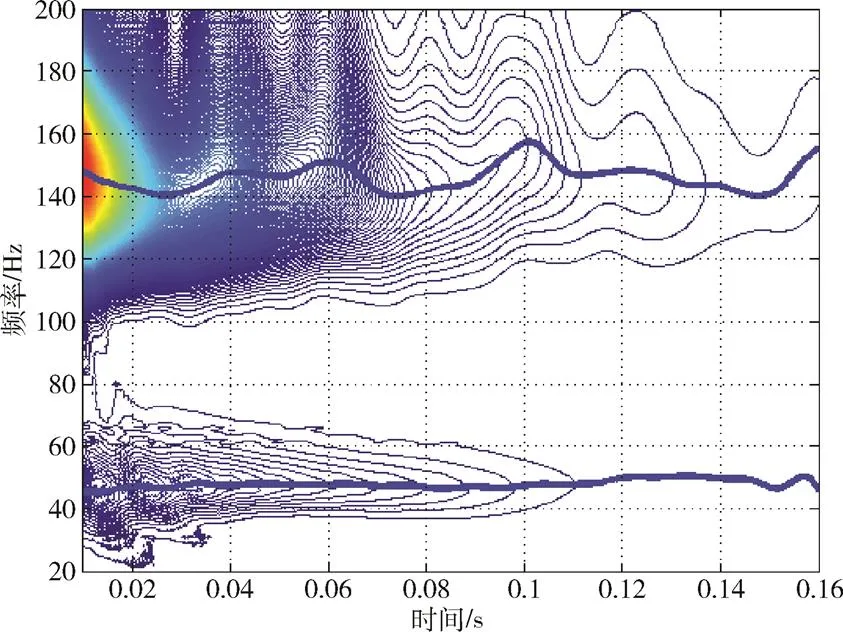
图8 自由衰减信号的功率谱等高线

在自由衰减信号连续小波变换的基础上，提取48Hz和146Hz附近的脊线，画出频率-时间曲线和幅值-时间曲线，见图9。

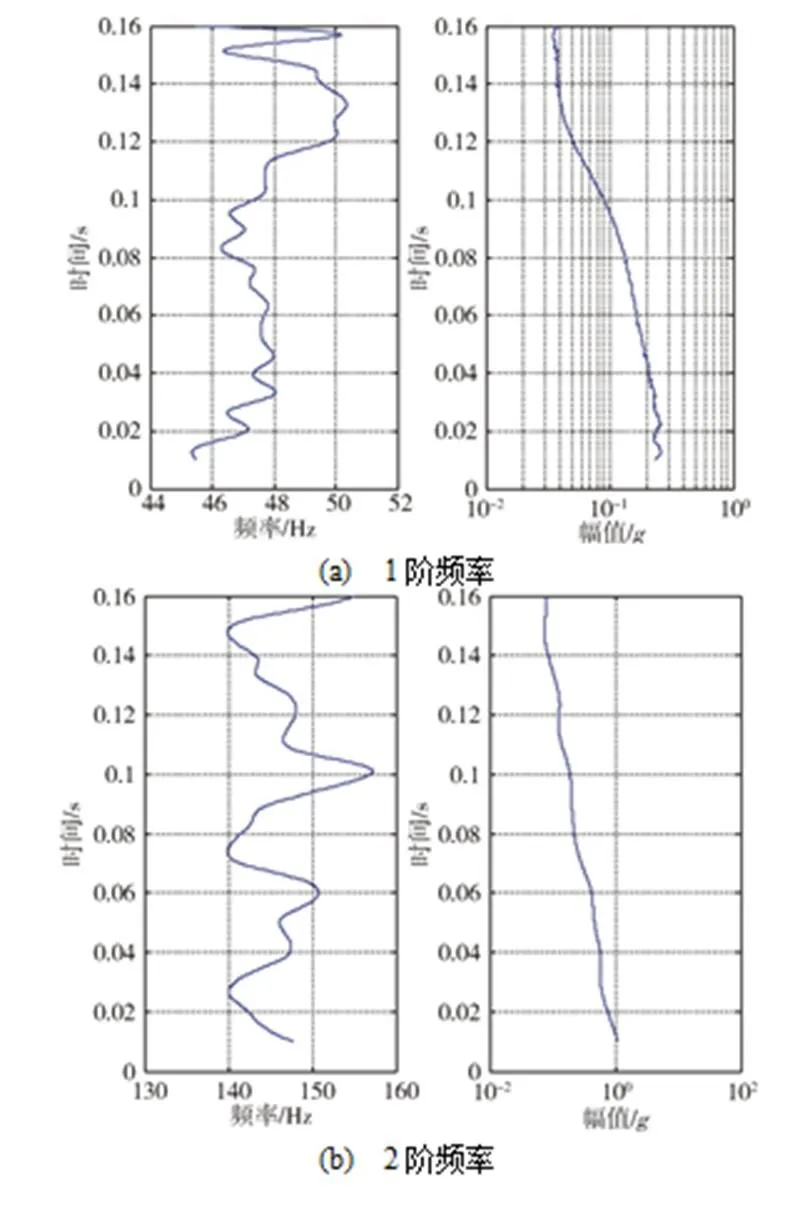
图9 振动频率和幅值随时间的变化

按照前述研究结论，时间初始阶段的频率和幅值识别具有更高的精度。共选取25个不同大小的参考幅值去截随机响应信号，得到不同幅值下的自由衰减信号；对不同的衰减信号进行小波变换，得到相应的两条脊线；提取每条脊线的初始部分进行平均，得到频率-幅值对应关系；将不同幅值对应的频率连续画出，得到图10所示的频率-幅值曲线。

图10反映了复合材料板的两阶主要频率的非线性特性：一阶频率随振动幅值的增加而提高，呈现刚度渐强非线性特性；二阶频率随振动幅值的增加而降低，呈刚度渐弱非线性特性。分别用式(13)拟合计算两阶频率对应的非线性刚度系数，(3/)1=4.21×107，(3/)2=-1.06×108。

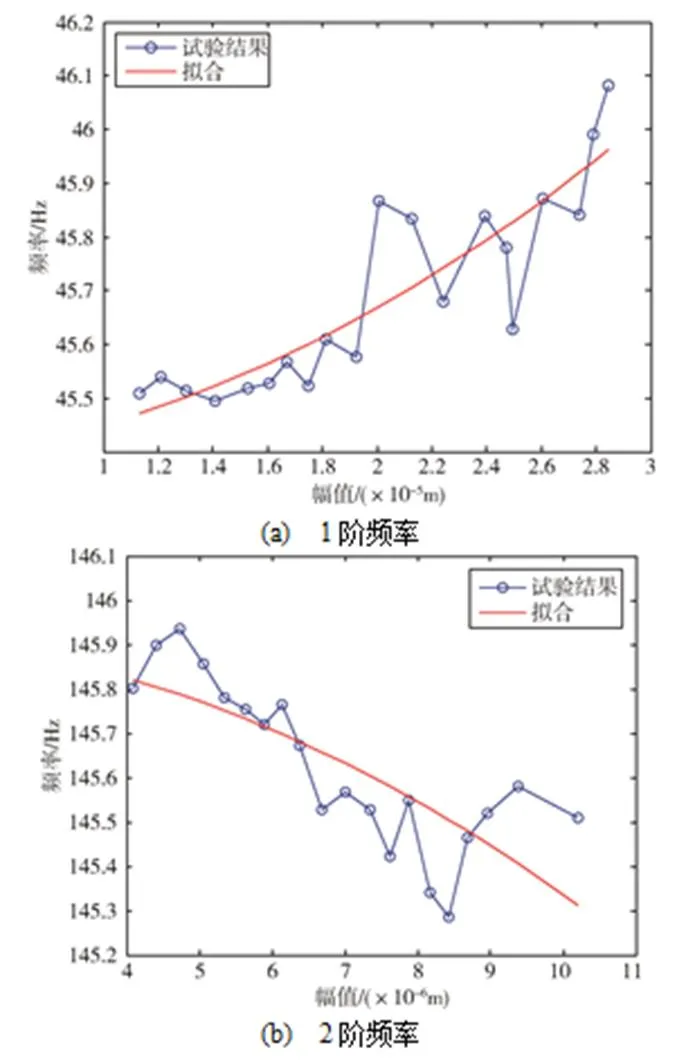
图10 频率随振动幅值变化

4 结论

1）本文分析了随机减量法在非线性系统中的适用性。计算结果表明，对于考虑刚度非线性的单自由度系统，随机减量法计算得到的自由衰减曲线在靠前的几个周期内具有较好的精度，算例前5个周期内幅值和频率计算误差在5%之内。

2）本文提出了随机振动响应下，基于随机减量法和连续小波变换的结构非线性特性分析方法，并用三次刚度单自由度非线性系统算例进行了验证。计算结果表明，分析方法具有一定的精度，对3次刚度3识别结果的偏差小于15%。

3）提出了多自由度结构的非线性特性分析方法，并设计试验进行了典型试验件的非线性特性分析。提取了复合材料板前2阶谐振频率对应的频率-幅值关系，分析了其对应的非线性特性差别。研究结果展示了随机振动环境下刚度非线性导致的多自由度系统响应的复杂性，对于结构非线性特征识别和建模具有参考价值。

[1] 李欣业, 陈予恕, 张琪昌. 火箭非线性动力学行为研究中的若干问题[J]. 河北工业大学学报, 2001, 30(6): 74-78

LI X Y, CHEN Y S, ZHANG Q C. Some topics on nonlinear dynamics of carrier rocker[J]. Journal of Hebei University of Technology, 2001, 30(6): 74-78

[2] 吴家驹, 张鹏飞, 付玮, 等. 非线性系统的频响函数分析[J]. 强度与环境, 2015, 42(4): 1-7

WU J J, ZHANG P F, FU W, et al. The frequency response function analysis of nonlinear system[J]. Structure & Environment Engineering, 2015, 42(4): 1-7

[3] 卫洪涛, 孔宪仁, 王本利, 等. 非线性连接结构对一个典型卫星频率漂移的影响[J]. 航天器环境工程, 2012, 29(3): 297-303

WEI H T, KONG X R, WANG B L, et al. Effect of nonlinearities in the joints on the amplitude-frequency response of a typical satellite structure[J]. Spacecraft Environment Engineering, 2012, 29(3): 297-303

[4] 樊文欣, 杨桂通, 赵俊生, 等. 金属橡胶减振器非线性建模及仿真研究[J]. 车用发动机, 2009(5): 53-56

FAN W X, YANG G T, ZHAO J S, et al. Nonlinear modeling and simulation of metal rubber damper[J]. Vehicle Engine, 2009(5): 53-56

[5] 韩德宝, 宋希庚, 薛冬新. 橡胶减振器非线性动态特性的试验研究[J]. 振动工程学报, 2008, 21(1): 102-106

HAN D B, SONG X G, XUE D X. Experiment on nonlinear dynamic characteristic of rubber isolator[J]. Journal of Vibration Engineering, 2008, 21(1): 102-106

[6] 张鹏飞, 苏华昌, 吴家驹. 基于奇异值分解的惯性测量组合减振系统非线性刚度识别[J]. 导弹与航天运载技术, 2016(3): 68-72

ZHANG P F, SU H C, WU J J. Identification of nonlinear stiffness of inertial measurement unit with vibration absorber system based on singular value decomposition[J]. Missiles and Space Vehicles, 2016(3): 68-72

[7] 黄方林, 何旭辉, 陈政清, 等. 随机减量法在斜拉桥拉索模态参数识别中的应用[J]. 机械强度, 2002, 24(3): 331-334

HUANG F L, HE X H, CHEN Z Q, et al. Application of random decrement technique to modal parameter identification of cables for a cable-stayed bridge[J]. Journal of Mechanical Strength, 2002, 24(3): 331-334

[8] 任向鑫, 闫维明, 何浩祥. 用随机减量法计算消能减振结构附加阻尼比[J]. 工业建筑, 2013, 43(增刊1): 133-137

REN X X, YAN W M, HE H X. Calculation of additional damping ratio of energy dissipation structure by random decrement method[J]. Industrial Construction, 2013, 43(Sup 1): 133-137

[9] 张家凡, 易启伟, 李季. 复解析小波变换与振动信号包络调解分析[J]. 振动与冲击, 2010, 29(9): 93-96

ZHANG J F, YI Q W, LI J. Complex analytic wavelet transform and vibration signals envelop-demodulation analysis[J]. Journal of Vibration and Shock, 2010, 29(9): 93-96

[10] LARDIES J, TA M N, BERTHILLIER M. Modal parameter estimation based on the wavelet transform of output data[J]. Archive of Applied Mechanics, 2004, 73(9/10): 718-733

[11] 陈前, 高雪. 结构动力学中的非线性问题[M]. 北京: 机械工业出版社, 2012: 42-46

（编辑：许京媛）

Identification of nonlinear parameters of structure based onrandom vibration response

ZHANG Pengfei, FU Wei, SU Huachang, WU Jiaju

(Beijing Institute of Structure and Environment Engineering, Beijing100076, China)

The composite material has typical nonlinear characteristics. Its nonlinear stiffness is very important for the system design and analysis. The random vibration is ubiquitous in the environment, and the identification of nonlinear parameters in the practical environment gives more reasonable results. A method of identification of nonlinear parameters based on the random decrement method and the continuous wavelet transform is presented. And a program of identifying the nonlinear stiffness based on the random vibration response is developed. A numerical example of a single freedom nonlinear system with cube stiffness is given to validate the method and the program. The nonlinear characteristics of the typical composite material structure are studied. It is shown that the method of identification of nonlinear parameters enjoys a high precision, and different resonant order of a multi freedom system has different nonlinear characteristics. The present method is useful for the nonlinear parameter identifying and modeling in a random vibration environment.

nonlinear stiffness; random decrement method; continuous wavelet transformation; simulation analysis; test validation

O235; O324

A

1673-1379(2017)06-0604-07

10.3969/j.issn.1673-1379.2017.06.006

张鹏飞（1986—），男，硕士学位，高级工程师，主要从事结构动力学试验与研究。E-mail: 350937943@qq.com。

2017-06-01；

2017-11-29