转子非线性扭转振动成因研究

刘 阳， 涂晓彤， 张 希， 李富才, 李鸿光

(上海交通大学机械系统与振动国家重点实验室 上海， 200240)

转子非线性扭转振动成因研究

刘 阳， 涂晓彤， 张 希， 李富才, 李鸿光

(上海交通大学机械系统与振动国家重点实验室 上海， 200240)

目前研究转子扭转振动的非线性现象，多数采用直接假设存在立方非线性，并未对其存在的原因进行解释。针对此问题，从几何变形的角度出发，推导出转子扭转振动中产生刚度渐软的duffing非线性现象的原因。首先，在未考虑非线性影响的情况下用ANSYS进行了模态求解；其次，在考虑非线性项时，建立多自由度的数学模型，采用模态截断的方法和多尺度法分析了系统的主共振；最后，通过数值仿真与扫频试验结果的定量对比，证明了转子扭转振动中存在刚度渐软的立方非线性理论的正确性。

扭转振动；非线性；多自由度模型；定量分析；扫频试验

引 言

随着机械工业的发展，转子系统朝着高速、重负荷、多转速的方向发展。近几十年来，在大型汽轮发电机组、机车船舶等都发生过主轴的断裂、飞脱等严重事故，对人身安全、国民经济造成巨大的损失。因而，由扭转振动引起的机械系统故障备受关注[1]。

通常分析加速转子的动力学响应时，主要采用线性的方法[2]或者非常简单的模型[3]，即Jeffcot转子模型，其在转动惯量很大的圆盘上加上一段无质量的轴。分析转子扭转振动的跳跃、滞回等现象时，多数采用直接假设存在立方非线性项[4]，然而未对其产生的原因进行研究。普遍的认识是不同的加速度使得转子的共振峰发生了偏移[5]，不同学者有不同的观点，例如转子在临界转速附近的阻尼是变化[6]的，转子材料的非线性[7]及duffing非线性的求解方法[8]等。笔者对转子的扭转几何变形未进行线性假设，考虑高次项给系统带来的非线性影响，并且对试验的转子系统进行合理的简化，建立了4个自由度的非线性动力学微分方程，采用模态截断的方法[9]将系统的自由度由繁化简，利用多尺度法对转子的非线性方程进行求解。最后对转子进行扫频试验，理论与试验结果相符。

1 非线性扭转振动的原因

当轴的两端受到方向相反、大小为T的扭矩时，假设变形后的截面依然是平面，截取长度为dx微元mmnn进行分析，其中,O1O2ABCD为未发生变形的楔形微元，变形后的微元为O1O2ABC′D′。AD与AD′的夹角即切应变γ，微元由于扭矩T的作用而产生的扭转角为dφ。微元模型如图 1 所示。切应变γρ应满足

tanγρ=dd′/ad=ρdφ/dx

(1)

图 1 微元的扭转变形Fig.1 Torsional deformation of element

其中：ρ为微元到几何中心的距离。

将式(1)进行Taylor展开

(2)

因为材料还处于弹性变形阶段，满足Hooke剪切定律

τρ=Gγρ

(3)

其中：G为材料剪切模量。

根据前面的假设，在截面上只有剪切应力，对剪切应力在整个截面上进行积分，可得

(4)

其中：Ip为极惯性矩。

当转轴在受到扭矩激励时会发生扭转振动[10]，如图 2所示，其中T，φ为关于x，t的函数，记为T(x,t)，φ(x,t)，则轴的扭转运动微分方程为

(5)

图2 轴的扭转振动Fig.2 Torsional vibration of shaft

其中：J0为单位长度的转动惯量；f为广义力(阻尼力)。

化简式(5)可得

∂T/∂x+f=J0∂2φ/∂2t

(6)

取自由边界的振型函数

υ1(x)=cos(πx/L)

(7)

将式(4) 代入式(6)中，再从0到L积分，可得

(8)

将其代入式(8)可得

(9)

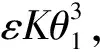
(10)

其中：|ε|≤1 且ε<0。

2 模型的建立

2.1 试验台

笔者分析的对象为一转子故障模拟多功能试验台，如图3所示，该转子系统具备扭转测试分析功能。

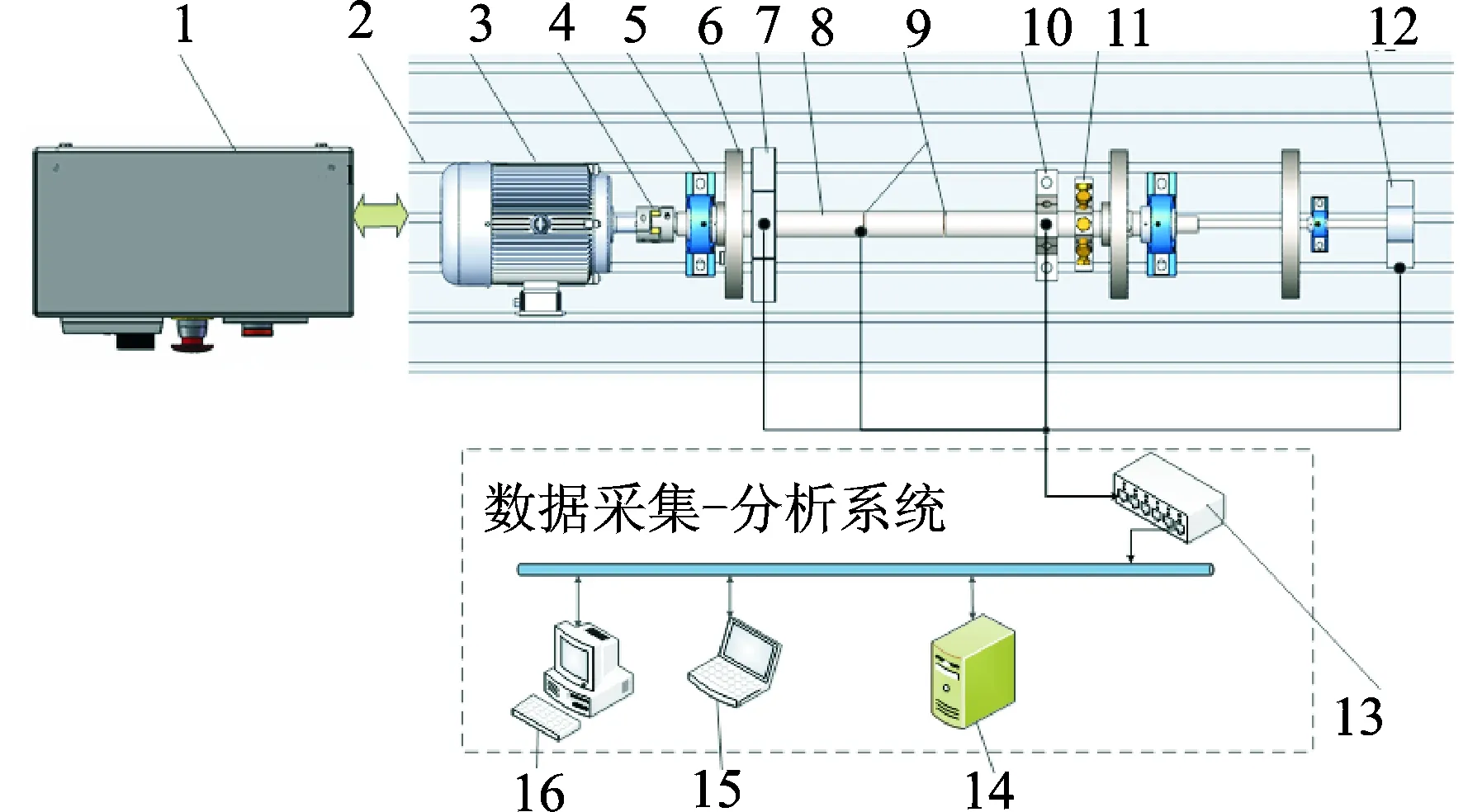
1-控制柜；2-T型槽平台；3-两极三相异步电动机；4-弹性联轴器；5-滑动轴承；6-动平衡圆盘；7-测速传感器支架；8-阶梯轴；9-扭振遥测装置；10-回旋振动传感器支架；11-碰磨实验支架；12-机械式扭振测试装置；13-数据采集卡；14-数据库；15-便携电脑；16-PC图 3 试验台结构图Fig.3 Structure graphing of vibration table

试验所用的两极三相异步电动机的转速范围为0～3 000 r/min，控制柜用于实现电控扭振激励的发生，以及相关参数如角加速度等的设置。

2.2 有限元线性模态分析

在ANSYS中对上述转子系统进行建模仿真分析，如图4所示。选用Beam188梁单元，对转子的前5阶扭转振动的固有频率和振型进行了分析。

图 4 转子的有限元模型Fig.4 Finite element model of rotor

在ANSYS里进行模态求解，得到模型的前5阶扭转振动的固有频率，如表 1所示。

表1转子的前5阶扭转振动的固有频率

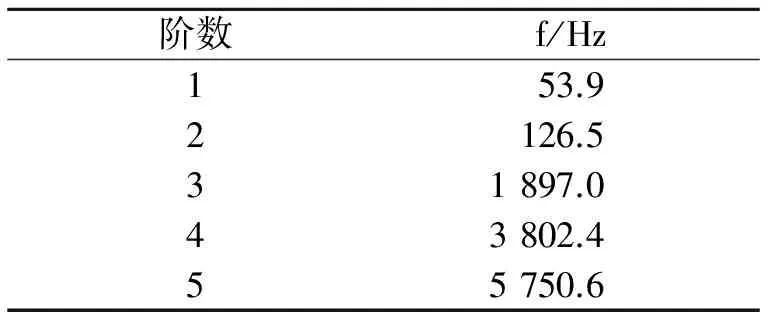
Tab. 1 Former five torsional natural frequency of rotor

选取转子扭转振动的第1阶振型进行展示，如图 5所示。

图 5 扭转振动的第1阶振型Fig. 5 Principal mode of torsional vibration

由表 1和图 5可知，若不考虑非线性因素的影响，转子第1阶扭转振动固有频率为53.9 Hz，其最大扭角出现在远离电动机的一端。

2.3 转子的数学模型

经过合理的简化，得到简化后的模型如图 6 所示，将转子简化为4个集中质量的圆盘和无质量的轴。考虑转子右端的联轴器及电机轴的转动惯量对系统的影响，所以简化成4个集中质量的圆盘，列出模型的运动微分方程

图6 转子的简化模型Fig.6 Simplify model of rotor

其中：Jpi,θi,i=1,2,3,4分别为各圆盘的等效转动惯量和扭转角；Kti,Cti,i=1,2,3 为各轴段的扭转刚度和扭转阻尼。

令φi=θi-θi+1,i=1,2,3代入式(11)消除转子的刚体转动，保留各圆盘之间的相对转角，并将其转换为矩阵的形式

(15)

其中 ：

式(15) 右端第1项为阻尼力项，第2项为非线性力项，第3项为驱动力项。为了对式(15)进行解耦，首先求转子在无阻尼自由振动情况下扭转振动的固有频率及其对应的振型。可由以下方程得到

|-ω2I3+K|=0

(16)

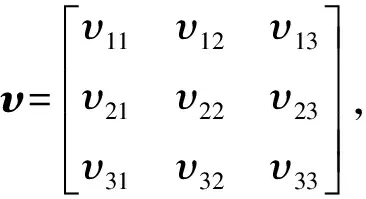
(17)

将方程写成矩阵的形式为

(19)

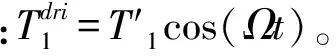
对式(19)采用非线性多尺度法可求得其1阶近似解，假设解的形式如下

(20)

其中：σ为激励频率失调参数。

(21)

考虑到此转子系统的扭转振动扫频试验为慢时变参数振动，所以有

(22)

将式(22)带入式(21)，消去λ，整理可得振幅a与激励频率Ω的关系

(23)

用Matlab编程计算得到频响曲线，见图 7。

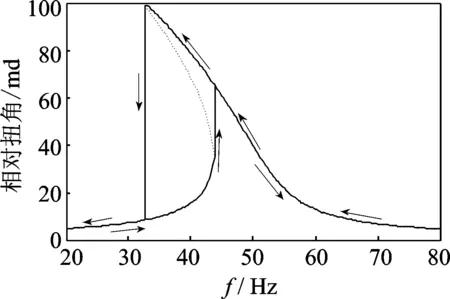
图 7 主共振附近的频响曲线Fig. 7 Frequency response of principal resonance

图 7中箭头的方向分别代表了转子的升速和降速的过程。在转子的非线性振动的求解过程中，对于固定的激励频率，其解可能有1个或3个。如图7中虚线部分对应的解为非稳定解，实线部分对应的解为稳定解。

在升速阶段的初期，转子的相对扭转振动值随转速升高基本保持不变。随着转速的增加，当遇到非稳定解时，相对扭转振动值会骤然增加跳跃至较高的另一个稳定解，因此在升速过程中呈现出跳跃现象。

在降速阶段，转子的相对扭转振动值随转速降低逐步升高，当遇到非稳定解时，相对扭转振动值会骤然降低至较低的另一个稳定解，因此在降速过程中呈现出跳跃现象。

3 扫频试验

为验证上述数学模型的正确性，对转子的扭转振动进行扫频试验，采用两极三相异步电机作为驱动，如图8所示。电机在转动的过程中，会激发出正序电流和负序电流，因此其相对频率为Fs-(-Fs)，所以激励频率为电机转速的2倍。计算主共振频率时，按照共振频率=共振转速×2÷60计算。

根据有限元软件分析得到的第1阶振型中，最大扭转角出现在转子的最左端，所以在末端安装ONO SOKKI编码器以得到转子的最大扭角。

图 8 试验测试Fig. 8 Picture of test

在本次扫频试验中，电机从0升速至3 kr/min，再从3kr/min降速至0，加速时间和减速时间均为600s，得到的扫频曲线如图 9所示。

图 9 扫频试验曲线Fig .9 Curve of frequency sweep test

从图 9中可以看出，转子的扫频曲线中存在跳跃现象；在升速阶段共振频率较大，共振峰值较小；降速阶段共振频率较小，共振峰值较大。把图 7的数值仿真数据与图 9的试验数据进行汇总和对比，结果如表 2所示。

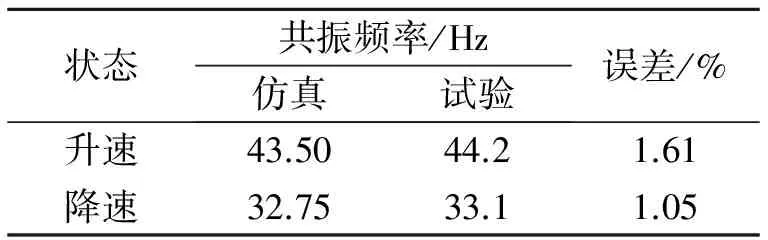
表 2 模型数值仿真与试验的对比

考虑扭转振动中刚度渐软的立方非线性后，数值仿真的结果(43.5Hz/升速，32.75Hz/降速)与试验结果(44.2Hz/升速，33.1Hz/降速)误差在2%以内，是吻合的。

4 结果的讨论与比较

1) 图7中骨架线的中线(即点画线)与x轴的交点为51.2Hz，与有限元线性求解结果是相符的。

2) 由于非线性振动分析中存在非稳定解，多以转子的临界转速会发生偏移，幅频响应中出现跳跃现象。升速的主共振频率要高于降速的主共振频率，但降速的主共振峰值要高于升速的主共振峰值。

3) 对比图7、图9和表2可知，数值仿真得到的非线性振动的特点在试验中均得到了验证。

5 结束语

从扭转振动的几何变形的角度出发，在未进行线性化假设的前提下，推导出转子扭转振动中存在刚度渐软的立方非线性项。通过数值仿真与试验对比验证了转子扭转振动中存在刚度渐软的立方非线性项的理论的合理性。在转子动力学设计方面应充分考虑几何尺寸带来的刚度渐软立方非线性的影响，避免转子系统扭转振动的共振频率出现在工作转速范围内，否则系统工作的安全性能将大大降低，甚至出现重大的安全事故。

[1] 张建平. 转子轴系扭振测量与控制的实验研究 [D]. 天津：天津大学, 2007.

[2] 冯栋梁, 魏来生. 传递矩阵法在动力传动系统扭振分析中的应用 [J]. 车辆与动力技术, 2010(1): 41-45.

Feng Dongliang, Wei Laisheng. Application of transfer matrix method in vehicle power train's torsional vibration analysis.[J].Journal of Vehicle & Power Technology,2010(1):41-45.(in Chinese)

[3] 张萌, 任兴民, 段向春. 单盘转子的瞬态不平衡动力相应分析 [J]. 机械科学与技术, 2006, 25(1): 116-118.

Zhang Meng, Ren Xinmin, Duan Xiangchun .Transient dynamic response of jeffcott rotor [J].Journal of Mechanical Science and Technology,2006,25(1):116-118. (in Chinese)

[4] 杨志安, 邱家俊, 李骊. 三圆盘扭振系统主共振的理论与实验研究 [J]. 应用数学和力学, 1998, 19(6): 505-511.

Yang Zhian, Qiu Jiajun, Li Li.A theoretical and experimental investigation of a primary resonance of a three circular plates torsion vibration system [J].Journal of Applied Mathematics and Mechanics, 1998, 19(6): 505-511. (in Chinese)

[5] 胡仲翔, 严普强. 对于用扫频激励法测试系统频率特性的讨论 [J]. 振动、 测试与诊断, 1985(1): 1-6．

Hu Zhongxiang, Yan Puqiang. A research about frequency sweep test [J]. Journal of Vibration, Measurement & Diagnosis, 1985(1): 1-6. (in Chinese)

[6] Genta G. On a persistent misunderstanding of the role of hysteretic damping in rotordynamics [J]. Journal of Vibration and Acoustics, 2004, 126(3): 459-461.

[7] 吴晓, 黎大志. 非线性材料圆杆的扭转固有振动分析 [J]. 振动与冲击, 2005, 24(3): 53-54.

Wu Xiao, Li Dazhi. Analysis of the natural twist vibration of round rod with nonlinear material [J]. Journal of Vibration and Shock, 2005, 24(3):53-54. (in Chinese)

[8] Cveticanin L. Analytic approach for the solution of the complex-valued strong non-linear differential equation of duffing type [J]. Physica A, 2001, 297: 348-360.

[9] Genta G, Delprete C. Acceleration through critical speeds of an anisotropic, non-linear, torsionally stiff rotor with many degrees of freedom [J]. Journal of Sound and Vibration, 1995, 180(3): 369-386.

[10] Rao S S,李欣业，张明路．机械振动[M]．4版.北京：清华大学出版社,2011:437-439．

10.16450/j.cnki.issn.1004-6801.2017.06.029

上海市科学技术委员会基础研究资助项目(15JC1402600)

2016-01-11；

2016-06-12

TH133.2; TH165.3

刘阳，男，1991年7月生，博士生。主要研究方向为旋转机械的动力学及结构健康监测。

E-mail：liuyangjiulong@sjtu.edu.cn