传感器催化特性差异对气动热影响的计算分析

丁明松，董维中，高铁锁，江 涛，刘庆宗

(中国空气动力研究与发展中心计算空气动力研究所， 绵阳 621000)

传感器催化特性差异对气动热影响的计算分析

丁明松，董维中，高铁锁，江 涛，刘庆宗

(中国空气动力研究与发展中心计算空气动力研究所， 绵阳 621000)

针对高温气体效应及壁面催化效应对气动热环境影响，考虑高温空气各种化学反应、分子振动激发、流动中的非平衡效应以及壁面催化复合反应，通过数值求解热化学非平衡N-S方程和壁面能量、质量平衡方程，完善了有限催化条件下高温热化学非平衡流场气动热环境数值模拟方法和程序。在此基础上，针对廉金属热电偶传感器热流测量问题，开展了不同条件下高超声速热化学非平衡流场气动热环境数值模拟，分析了催化特性差异对局部气动热环境(传感器表面热流)的影响规律，为试验数据的误差带分析、修正处理和使用提供参考。研究表明：1)催化特性差异会给局部区域带来很强质量扩散热流，使总热流发生跳变，给传感器热流测量带来不可忽视的误差；2)材料催化特性差异越大，热流跳变量越大，某些条件下时，局部热流值将远远高于全表面FCW模拟的结果，其影响量可达100%以上；3)本文计算条件下，飞行马赫数越大、飞行高度越低，催化特性差异的影响越大；4)催化特性差异带来的影响还与飞行攻角、飞行器表面温度等因素存在一定关联，在催化复合系数相同情况下，表面温度越高，影响量越大。

热流传感器；气动热环境；高温气体非平衡效应；催化效应；数值模拟

0 引 言

高超声速飞行器在再入和滑翔过程中，如果飞行速度很高(一般认为马赫10以上)，会出现高温气体非平衡效应[1-4]。高温下化学反应的吸热效应、气体分子的振动模态激发以及混合气体非完全气体特性会对飞行器气动力、热等特性造成显著影响[5-7]。高温气体流场中原子和离子在到达壁面时会发生催化复合反应(即壁面催化效应)，释放出很大的结合能，不仅影响非平衡流动，而且产生较大组分扩散热流，使飞行器表面气动热环境更加严酷[8]。

研究高温气体非平衡效流动中壁面催化效应对飞行器气动热环境的影响，一直都是高超声速飞行器研究的热点。在数值模拟中，催化效应常以边界条件形式给出。完全催化(Fully Catalytic Wall,FCW)和完全非催化(Non-Catalytic Wall,NCW)是最容易实现的两种壁面催化边界条件，应用十分广泛。但这两者只模拟了壁面催化的两种极限状态，要精确模拟催化效应，还须考虑壁面材料具体的催化特性，采用有限催化条件(Partially Catalytic Wall,PCW)边界计算模型。根据催化复合反应速率常数计算方法不同，有限催化条件及其模型主要分为两种：一种是指定催化复合系数，考虑气体分子热运动碰撞频率，得到催化反应速率常数[9-10]；另一种是通过气固催化复合反应过程的建模分析，采用有限速率化学反应动力学方法，计算催化反应速率常数[11]。第一种方法相对简单，有大量材料催化系数试验数据支持[12]，因此应用较为广泛[13-14]。

在气动热环境的预测和分析过程中，表面热流的试验测量(包括飞行试验和地面试验)是必不可少的研究手段。利用热电效应制成的热电偶，是目前应用最广泛的检测元件[15]。例如，镍铬-镍硅热电偶(K型)是目前用量最大的廉金属热电偶[15-16]；铜-康铜热电偶(T型)是中低温区最佳的廉金属热电偶[17]。对于高超声速非平衡流动来说，由于金属铜或镍等材料的催化特性较强[8,18](常近似认为具有完全催化能力)，而飞行器表面的隔热材料，如硅基、碳基材料等表面催化复合系数一般在0.1以下[9-10,19-20]；碳化硅陶瓷涂层，在被动氧化条件下，表面产物为二氧化硅，可视为完全非催化壁面[8]。这种情况下，热流传感器(K型或T型热电偶)的测量面与飞行器表面隔热材料之间的催化特性存在较大差异。在表面热流的试验测量过程中，如果采用接触式测量技术，热流传感器的测量面将替代飞行器某一局部区域表面。此时，由于两者催化特性差异，高超声速飞行器的局部气动热环境可能发生变化，热流传感器测得的热流，可能与飞行器表面无传感器测量时的热流存在一定差别。

在高温气体效应以及壁面催化效应方面，国外研究水平较高，形成了一些较为成熟的流场软件，如美国LAURA软件[21]、SPARTA软件[22]等。国内近十几年来也有不少学者开展这方面的研究，如董维中[23]、高冰[24]、苗文博[25,26]、杨肖峰[27]等，取得了很多有价值的结论。在热电偶精准测量方面，国内研究也比较多。如2013年，张洪俊等[28]开展了镍铬-镍硅热电偶(K型)检定过程中的测量不确定度评定研究。2014年，宋川川等[29]开展了铜-康铜热电偶热镀锡膜焊及其性能对比研究。

尽管国内在高温非平衡效应及表面催化效应、热电偶精准测量方面取得了非常大的发展，但很少见到针对热流传感器测量面与飞行器隔热材料催化特性差异问题开展催化特性差异对局部气动热环境影响的研究，其作用大小和影响规律尚不十分明确。

在以前工作中，作者所在研究团队对高温气体效应、壁面催化效应和高超声速飞行器气动热环境进行了研究[5-8,23,30-31]。本文在此基础上，完善高温气体热化学非平衡流场气动热环境数值计算方法和程序，针对廉金属热电偶传感器测量面与飞行器表面隔热材料催化特性差异性问题，开展不同条件下高温气体热化学非平衡流场气动热环境数值模拟，分析催化特性差异对流场局部气动热环境(传感器表面热流)的影响规律，为试验数据的误差带分析、修正处理和使用提供参考。

1 数值计算方法

控制方程是三维热化学非平衡Navier-Stokes方程，其无量纲化形式为[5]：

式中：Q为守恒变量向量,Re是雷诺数，F,G,H和FV,GV,HV分别对应三个方向的对流项和黏性项，W为热化学非平衡源项。对流项采用AUSMPW+格式离散，黏性项采用中心格式离散，时间离散采用LU-SGS隐式方法。为了克服方程刚性，非平衡源项、对流项和黏性项均采用全隐式处理。具体处理方法详见文献[5]。

2 物理化学模型

2.1 热化学反应模型

气体模型选用5 组分或7 组分的空气模型，化学反应模型采用Dunn-Kang模型[5]或Park模型[32]。第i个化学反应生成源项为：

(2)

2.2 表面催化模型和表面温度计算方法

NCW和FCW处理详见文献[5]。对于有限催化PCW，主要考虑氮原子(N)和氧原子(O)复合反应以及电离组分的复合反应[33]：

反应速率常数形式为：

(3)

式中:αr是壁面催化复合系数，αr=0～1或壁面温度Tw的函数(来源于试验拟合数据)。M1、M2和M3分别为O、N和NO的摩尔分子质量。组分质量通量可写为：

(4)

3 计算方法校验

采用球头模型[33]，半径5.08 cm，开展了非平衡流场气动热环境数值模拟考核，重点在于有限催化条件模拟。计算来流：温度970 K，振动温度2800 K，压力96.12 Pa，速度5630 m/s。壁面温度1000 K，采用5 组分空气模型，与文献[33]一致；化学反应模型分别采用Dunn-Kang模型或Park模型；考虑两温度热力学非平衡模型；壁面催化条件为NCW、FCW以及PCW。考虑有限催化(PCW)时，催化复合系数为0.0001～1.0。

图1给出了驻点线氮气质量分数分布和流场温度云图，R为球头半径。可以看出，流场中温度可达13000 K，N2存在较大程度的离解，随壁面催化复合系数减小，离解程度增大。图2(a)给出了表面热流分布，S为表面弧长。图2(b)为不同催化复合系数条件下的驻点热流，横轴αr是壁面催化复合系数，Q0为完全催化条件下驻点热流。可以看出，本文计算的热流分布与文献符合较好，不同催化条件下的变化规律与文献基本完全一致，这说明本文数值计算结果具有较高可信度。

4 催化特性差异对局部气动热环境影响分析

计算外形如图3(a)所示，头部尖端圆弧半径5 mm，上表面长度500 mm，下表面长度370 mm，上下表面之间厚度约50 mm。图3(a)中黑色圆点区域为热流传感器测量面，具体可采用镍铬-镍硅热电偶(K型)或铜-康铜热电偶(T型)。测量面半径为5 mm，中心点距头部前端点300 mm，距后端底部200 mm，距左右两端100 mm。图3(b)给出了热流传感器铜-康铜热电偶(T型)示意图，测量方式为嵌入式测量，测量面与被测物面齐平，材料为康铜合金。

计算飞行高度45～65 km，来流马赫数12～22，飞行攻角-15～10°，壁面温度为等温壁300～1500 K或者辐射平衡温度。采用两温度模型和7 组分Dunn-Kang模型开展热化学非平衡流动数值模拟。

由于金属铜或金属镍的催化特性很强,这里近似认为热流传感器测量面为完全催化壁面条件(FCW)。数值模拟气动热环境时,表面隔热材料的催化特性分别采用FCW、NCW和PCW;采用PCW时,催化复合系数为0.0001～1.0。

图4给出了飞行高度50 km、马赫数 18、攻角-15°、壁面温度300 K、隔热材料催化复合系数为0.001、传感器测量表面为FCW时热流分布云图，由图可以定性的看出，在材料催化特性差异作用下，传感器测量面上的热流远远高于周围附近区域，说明此时传感器测量到的表面热流并不是无传感器测热时实际状态的热流，传感器测热面与表面隔热材料之间的催化特性差异会对传感器热流测量带来很大的误差。

为进一步定量分析，图5给出了飞行高度50 km、马赫数 18、攻角-15°、壁面温度300 K时传感器测量面区域流向对称线上的热流分布，曲线标号FCW和NCW分别对应全表面(隔热材料和测量面)FCW和NCW的结果，αr=0.001对应隔热材料催化复合系数为0.001、传感器测量表面为FCW的结果，其它标号含义与此类似。由于传感器测量得到的热流为测量面平均热流，因此，本文图6给出了该飞行条件下隔热材料不同催化复合系数时传感器测量面平均热流Q和由催化特性差异引起的误差D(式(5)，将全表面完全催化数值计算得到的传感器测量面平均热流Q1作为参考值)，图中横坐标为隔热材料催化复合系数。

(5)

由图5和图6可以看出：隔热材料催化复合系数差异会带来局部热流的跳变，使其远远高于全表面FCW和NCW结果；材料催化特性差异越大(隔热材料αr越小)，热流跳变越高，某些情况下其差别(峰值)接近1 个量级，这会给传感器热流测量带来不可忽视的误差，例如隔热材料αr=0.001时， 误差D可达到100%以上。

为了分析测量误差产生的原因，图7给出了该飞行条件下流场中高能粒子氧原子O质量分数云图。图7(a)为隔热材料催化复合系数0.001、测量面FCW时全流场氧原子云图，图中圆圈标出位置为传感器所在区域，为了开展对比分析，图7(b)、7(c)和7(d)分别给出了不同催化条件下该区域的放大图。图7(b)和7(c)分别为传感器测量表面FCW时隔热材料催化复合系数0.001和0.01的结果，图7(d)全表面完全催化的结果。可以看出，当隔热材料催化复合系数0.001、传感器测量表面FCW时(图7(b))，由于隔热材料较低的催化特性，高能粒子(以O为例)在壁面处复合程度相对较低，流场中的浓度较高。高浓度的高能粒子流经传感器测量面(FCW)所在区域，就会发生大量复合反应，释放出化学能，使热流显著提升。由于此时，该区域附近流场中高能粒子浓度远高于全表面FCW条件下(图7(d))的结果，因此，传感器测量面热流将远高于全表面FCW时计算结果。由图7(b)和图7(c)还可以看出，隔热材料催化能力越弱，同等条件下，流场中的高能粒子浓度就越高，在传感器测量面(FCW)所在区域复合反应就越强，测量面热流跳变也就越大。

由于催化效应强弱不仅受表面材料的催化特性(催化复合系数)影响，而且受飞行速度、高度、飞行姿态和表面温度等影响非平衡效应因素影响。因此，本文接下来将开展不同飞行条件下催化特性差异对局部气动热环境(传感器表面热流)的影响分析。

4.1 不同马赫数条件下的影响分析

图8给出了飞行高度50 km、攻角-15°、壁温300 K时不同马赫数条件下传感器测量面平均热流Q及误差D，图中Q1为全表面完全催化时测量面平均热流，Q2为全表面催化系数0.001时测量面平均热流，Q3为隔热材料催化复合系数0.001、传感器测量表面FCW时测量面平均热流。催化特性差异引起的误差D，因参考值不同，可写为D1和D2，具体形式见式(6)。图9给出了不同马赫数时流场中温度最大值Tmax、主要组分(O2和N2)离解率最大值d以及来流总温To。

(6)

由图8可以看出，高度50 km时，随着马赫数增大，催化特性差异引起的热流测量误差显著增大：飞行马赫数10时，D1和D2均接近于0；马赫数12至16时，误差上升迅速；马赫数18至20，误差变化相对平缓；马赫数20时，D1和D2分别可达120%和150%左右。这一变化规律可结合图9进行分析：马赫10时，来流总温较低，流场中温度较低，氧气和氮气最大离解程度接近于0，流场中高能粒子(O原子和N原子等)接近于零，催化复合效应整体很弱，因此，由材料催化特性差异引起的测量误差接近于0。随着马赫增大，来流总温迅速升高，流场中温度上升，氧气和氮气离解程度迅速变大，流场中高能粒子浓度变大，壁面催化复合效应整体变强，因此由材料催化特性差异引起的测量误差也迅速增大。由于马赫数16时流场中O2最大离解率达95%以上，几乎全部离解，随马赫数进一步升高，流场氧气的离解程度只能缓慢接近100%，因此，马赫数18至20，误差变化相对平缓。

4.2 不同高度条件下的影响分析

图10给出了马赫数18、攻角-15°、壁温300 K时不同飞行高度条件下传感器测量面平均热流及误差，图中曲线标号含义与图8相同。图11给出了该条件下高温气体非平衡流场中氮气与氧气离解率最大值以及来流密度随马赫数的变化情况。

由图10可以看出，随飞行高度上升，催化特性差异引起的热流测量误差显著下降：高度45km时，D1和D2分别接近140%和190%，而高度65 km时，D1和D2仅16%和20%左右。这一规律可结合式(2)、式(4)和图11进行解释：由式(2)和式(4)可知，在其它因素相差不大的情况下(马赫数18时，飞行高度45～65 km流场中最大温度均在11 000～12 000 K左右)，密度越小，化学反应生成源项和壁面催化复合反应质量通量越小，也就是说这种情况下，气体密度越小，化学反应越弱。由图11可知，飞行高度45～65 km，空气密度下降1 个量级以上，因此氧气和氮气的离解率随高度上升显著下降，流场中高能粒子浓度降低，催化复合反应整体减弱，由材料催化特性差异引起的测量误差也迅速减小。

4.3 不同飞行姿态条件下的影响分析

图12给出了飞行高度50 km、马赫数18、壁温300 K时不同飞行攻角条件下传感器测量面平均热流及误差，图中曲线标号含义与图8相同。

由图可以看出，飞行攻角-15°至5°，传感器测量面平均热流下降，但相对误差D1和D2却逐步上升，由-15°时的120%和150%左右，上升至5°攻角的300%和550%以上。由此可见，尽管测量面背风时，平均热流较低，但在本文计算条件下，其受催化特性差异影响的相对误差更大。可从两个方面进行分析：一是热流的构成存在差别：测量面迎风时，温度传导热流在总热流中的占比较大，组分扩散热流占比相对较小，例如全表面FCW条件，攻角-15°时，测量面组分扩散热流占总热流18.7%，而攻角5°时组分扩散热流占比为33.1%，由于材料催化特性差异主要影响组分扩散热流，因此在测量面背风时，催化特性差异影响更为明显；二是无催化特性差异影响时，背风时测量面热流远远小于迎风时热流，当测量面背风时，尽管催化特性差异导致的热流绝对差量比迎风时小，但由于背风时的Q1和Q2很小，因此，其相对误差很大。

4.4 不同表面温度条件下的影响分析

图13给出了飞行高度50 km、马赫数18、攻角-15°时冷壁Tw=300 K(Case1)和热壁Tw=1500 K(Case2)条件下传感器测量面平均热流及误差，误差D计算见式(5)。可以看出：在本文的计算条件下，催化特性差异性带来的误差与表面温度存在一定关联，在催化复合系数相同情况下，表面温度越高，误差越大，例如隔热材料αr=0.01时，对于冷壁(Tw=300 K)，D为60.09%，对于热壁(Tw=1500 K)，D为88.46%。由图13还可以看出，隔热材料为完全催化FCW(αr=1)和完全非催化NCW(αr=0或者接近NCW的αr=0.0001～0.001)时，测量面热壁热流低于冷壁热流，这符合一般的认知；但当隔热材料催化系数αr=0.01、0.05和0.1时，测量面热壁热流反而高于冷壁热流。

这里可结合复合反应速率和组分质量通量(式(3)和(4))进行分析，以氧原子质量通量为例：

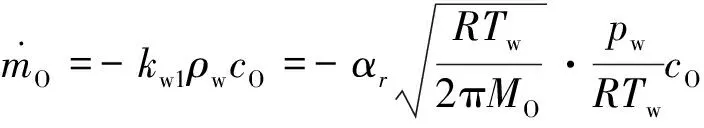
(7)

5 结 论

通过本文的研究，可以得到以下结论：

(1)完善了高温热化学非平衡流场有限催化气动热环境数值计算方法和计算程序。考核校验表明：壁面有限催化条件下热化学非平衡流场气动热环境数值计算结果与文献符合良好，可信度高。

(2)针对热流传感器，分析了多种条件下催化特性差异性对局部气动热环境(传感器表面热流)的影响，为试验数据的误差带分析、修正处理和使用提供参考。研究表明，在本文的计算条件下：1)催化特性差异会给局部区域(传感器测量面)带来很强质量扩散热流，使总热流发生跳变，给热流测量带来不可忽视的误差，在试验方案设计或数据处理过程中必须考虑传感器测量面和隔热材料催化特性差异带来的影响；2)催化特性差异越大，热流跳变量越大，某些情况下，局部区域(测量面)热流值甚至远远高于全表面FCW模拟时相同区域的结果；3)飞行马赫数越大、飞行高度越低，由催化特性差异引起的误差越大，其影响呈非线性关系，与流场中化学反应强度密切相关；4)催化特性差异性带来的误差还与飞行攻角、飞行器表面温度等因素存在一定关联：测量面背风时，催化特性差异的影响更显著；在催化复合系数相同情况下，表面温度越高，误差越大。

[1] Boyd I D. Modeling of associative ionization reactions in hypersonic rarefied flows [J]. Physics of Fluids，2007,19(9):3-14.

[2] Ozawa T, Levin D A, Nompelis I, et al. Particle and continuum method comparison of a high altitude Mach number reentry flow [J]. Journal of Thermo-physics and Heat Transfer. 2010, 24(2):225-240.

[3] Lofthouse A J, Scalabriny L C, Boyd I D. Hypersonic aerothermodynamics analysis across non-equilibrium regimes using continuum and particle methods [R]. AIAA 2007-3903, 2007.

[4] Wen C Y, Massimi H S, Chen Y S, et al. Numerical simulations of non-equilibrium flows over rounded models at reentry speeds [R]. AIAA 2012-5906, 2012.

[5] 董维中. 热化学非平衡效应对高超声速流动影响的数值计算与分析[D]. 北京: 北京航空航天大学, 1996. [Dong W Z. Numerical simulation and analysis of thermo-chemical non-equilibrium effects at hypersonic flows [D]. Beijing: Beijing University of Aeronautics and Astronautics, 1996.]

[6] 董维中. 气体模型对高超声速再入钝体气动参数计算影响的研究[J]. 空气动力学学报，2001，19(2): 197-202. [Dong W Z, Thermal and chemical model effect on the calculation of aerodynamic parameter for hypersonic reentry blunt body [J]. Acta Aerodynamica Sinica. 2001，19(2): 197-202.]

[7] 董维中，高铁锁，丁明松，等. 高超声速非平衡流场多个振动温度模型的数值研究[J]. 空气动力学学报, 2007, 25(1):1-6. [Dong W Z, Gao T S, Ding M S, et al. Numerical studies of the multiple vibrational temperature model in hypersonic non-equilibrium flows[J]. Acta Aerodynamica Sinica, 2007, 25(1):1-6.]

[8] 乐嘉陵. 再入物理[M]. 北京: 国防工业出版社, 2005: 9-21.

[9] Kurotaki T. Construction of catalytic model on SiO2-based surface and application to real trajectory[C]. 34th AIAA Therm-physics conference， Denver CO， June 19-22, 2000．

[10] Kurotaki T, Matsuzaki T. CFD evaluation of catalytic model on SiO2-Based TPS in arc-heated wind tunnel[R]. AIAA 2003-155, 2003

[11] Jochen M, Matthew M. Finite-rate surface chemistry model I: formulation and reaction system examples[R]. AIAA 2011-3783, 2011.

[12] Stewart D A. Surface catalysis and characterization of proposed candidate TPS for access-to-space vehicles[R]. NASA TM-112206, 1997.

[13] Stewart, D A. Effect of non-equilibrium flow chemistry and surface catalysis on surface heating to AFE[R]. AIAA 91-1373, 1991.

[14] Antonio V. Effect of finite rate chemical models on the aero thermodynamics of reentry capsules[R]. AIAA 2008-2668, 2008.

[15] 唐兆廷. 航天器用热电偶测温仪的设计[D]. 西安： 西安电子科技大学, 2011. [Tang Z T. The design of spacecraft thermocouple thermometer[D]. Xi’an: Xidian University, 2011.]

[16] 尹福炎. 热流传感器及其应用概况[J]. 传感器世界, 2000:7-13. [Yin F Y. Heat flux transducer and application[J]. Sensor World, 2000:7-13]

[17] 吴健. 热流传感器系统的研究[D]. 太原： 中北大学，2012.6. [Wu J. The research of heat flux sensor system[D]. Taiyuan: North University of china, 2012.6.]

[18] 金华. 防热材料表面催化特性测试与评价方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2014. [Jin H. Surface catalytic properties testing and characterization methods of thermal protection materials[D]. Harbin： Harbin Institute of Technology, 2014.]

[19] Stewart D A, Rakich J V, Lanfranco M J. Catalytic surface experiment on the space shuttle[C]．Palo Alto，Calif., June 23-25, 1981.

[20] Scott C D. Wall catalytic recombination and boundary conditions in non-equilibrium hypersonic flow with applications[C]. The Third Joint Europe/US Short Course in Hypersonic, Boston, 1990．

[21] Edquist K T. Afterbody heating predictions for a Mars science laboratory entry vehicle[R]. AIAA 2005-4817, 2005.

[22] Subrahmanyam P. Development of a parallel CFD solver SPARTA for aerothermodynamic analysis[R]. AIAA 2007-2976, 2007.

[23] 董维中，乐嘉陵，刘伟雄. 驻点壁面催化速率常数确定的研究[J]，流体力学实验与测量, 2000,14(3):1-6.[Dong W Z, Le J L, Liu W X. The determination of catalytic rate constant of surface materials of testing model in the shock tube [J], Experiments and Measurements in Fluid Mechanics, 2000,14(3):1-6.]

[24] 高冰，杭建，林贞彬，等. 高温真实气体效应中催化效应对气动热影响的实验探索[J], 流体力学实验与测量, 2004, 18(2): 55-58. [Gao B, Hang J, Lin Z B. The experiment exploration of catalyst effects on aerodynamic heat in real gas effects [J]. Experiments and Measurements in Fluid Mechanics. 2004, 18(2): 55-58. ]

[25] 苗文博，程晓丽，艾邦成，等. 高超声速流动壁面催化复合气动加热特性[J]. 宇航学报, 2013, 34(3):442-446. [Miao W B, Cheng X L, Ai B C, et al. Surface catalysis recombination aero-heating characteristics of hypersonic flow[J]. Journal of Astronautics, 2013, 34(3):442-446.]

[26] 苗文博，罗晓光，程晓丽，等. 壁面催化对高超声速飞行器气动特性影响[J]. 空气动力学学报, 2014, 32(2): 236-239. [Miao W B, Luo X G, Cheng X L, et al. Surface recombination effects on aerodynamic loads of hypersonic vehicles[J]. Acta Aerodynamica Sinica. 2014, 32(2): 236-239]

[27] 杨肖峰，唐伟，桂业伟，等. 火星环境高超声速催化加热特性[J]. 宇航学报, 2017, 38(2)：205-211. [Yang X F, Tang W, Gui Y W, et al. Hypersonic catalytic aero-heating characteristics for mars entry process[J]. Journal of Astronautics, 2017, 38(2)：205-211.]

[28] 张洪俊，陈红. K型热电偶检定过程中的测量不确定度评定[J]. 理化检验(物理分册),2012,48(12):797-800. [Zhang H J, Chen H. Measurement uncertainty evaluation of K-type thermocouple in verification[J]. Physical Testing and Chemical Analysis(Part A:Physical Testing), 2012, 48 (12) :797-800]

[29] 宋川川, 李永新. 铜-康铜热电偶热镀锡膜焊及其性能对比研究[J]. 电子测量技术,2014,37(4):15-18. [Song C C, Li Y X. Hot tinning welding method of copper-constantan thermocouples and performance research by comparison[J]. Electronic Measurement Technology, 2014,37 (4):15-18]

[30] 董维中，丁明松，高铁锁，等. 热化学非平衡模型和表面温度对气动热计算影响分析[J]. 空气动力学学报, 2013, 31(6):692-698. [Dong W Z, Ding M S, Gao T S, et al. The influence of thermo-chemical non-equilibrium model and surface temperature on heat transfer rate [J]. Acta Aerodynamica Sinica. 2013, 31(6):692-698.]

[31] 董维中，高铁锁，丁明松，等. 高超声速飞行器表面温度分布与气动热耦合数值研究[J]. 航空学报，2015，36(1):311-324. [Dong W Z, Gao T S, Ding M S, et al. Numerical study of coupled surface temperature distribution and aerodynamic heat for hypersonic vehicles [J]. Acta Aeronautica Et Astronautica Sinica, 2015, 36(1):311-324.]

[32] Park C. Review of chemical-kinetic problems of future NASA missions I: Earth entries [J]. Journal of Thermophysics and Heat Transfer, 1993 7(3): 385-398.

[33] Gokcen T. Effects of flow field non-equilibrium on convective heat transfer to a blunt body[R], AIAA 96-0325, 1996.

ComputationalAnalysisofInfluenceonAero-ThermalEnvironmentsCausedbyCatalyticPropertyDistinctionofHeatFluxSensor

DING Ming-song, DONG Wei-zhong, GAO Tie-suo, JIANG Tao, LIU Qing-zong

(Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China)

Considering high temperature air chemical reactions, gas molecules vibrational excitation, non-equilibrium effects in the flow and the catalytic effect on the vehicle surface, the numerical simulation method and the corresponding computational codes are developed for the aero-thermal environment of the thermo-chemical non-equilibrium flow by solving 3-D thermochemical non-equilibrium Navier-Stokes equations and the mass and energy balance on the surface of the vehicle. The numerical results of the typical example are inconsistent well with the foreign reference data. On this basis, the influence of the local catalytic property distinction is studied for the aero-thermal environment of a hypersonic vehicle with the heat flux sensor under different conditions. These results show that the local catalytic property distinction could obviously lead to the jump heat flux. In some cases, when the local catalytic property distinction is larger, the heat flux is far higher than the result under the full catalytic surface condition of the whole vehicle surface. In the conditions of this paper, it is found that the lower the flight altitude and the greater the Mach number is, the more obvious the influence caused by the catalytic property distinction is. The influence degree is also relevant to the flight attack angle and the surface temperature. Under the similar conditions, the influence degree is more obvious when the surface temperature is higher.

Heat flux sensor; Aero-thermal environment; High temperature gas effect; Catalytic effect; Numerical simulation

2017- 07- 27;

2017- 10- 13

V411.3; O354.7

A

1000-1328(2017)12- 1361- 11

10.3873/j.issn.1000- 1328.2017.12.014

丁明松(1983-)，男，博士生，助理研究员。主要从事气动物理理论与计算工作。

通讯地址：四川绵阳涪城区剑门路西段278号A4-2405(4号门)

电话：13778066924

E-mail: dingms2008@qq.com