基于毕卡迭代的捷联姿态更新精确数值解法

严恭敏，翁 浚，杨小康，秦永元

(西北工业大学自动化学院，西安 710072)

基于毕卡迭代的捷联姿态更新精确数值解法

严恭敏，翁 浚，杨小康，秦永元

(西北工业大学自动化学院，西安 710072)

针对捷联惯导在大角度机动等场合下姿态精确求解问题，论文根据四元数微分方程的毕卡级数解法，提出一种新的求解姿态更新的数值算法。新算法利用角增量建立角速度多项式拟合，再根据多项式四元数的乘法特点将其变换为多项式的卷积运算，求得更新四元数的幂级数解。新算法在推导过程中未做任何近似和假设，不存在原理性误差。在大幅值圆锥运动和大角度机动环境下，新算法与传统算法进行了对比仿真试验，校验了新算法具有明显的精度优势。

捷联姿态更新算法；毕卡级数；多项式拟合；仿真试验

0 引 言

捷联惯导算法的关键在于姿态更新算法，也即刚体定轴转动问题，多年来学者们对其进行了广泛而深入的研究[1]。描述姿态变换的数学工具有欧拉角、方向余弦阵、罗德里格参数、四元数和等效旋转矢量等,求解姿态数值更新的方法有一阶欧拉法、四阶龙格-库塔法、毕卡级数法和等效旋转矢量算法等。

目前，最为流行的姿态更新求解方法是：先使用陀螺角增量多子样采样计算等效旋转矢量，补偿转动不可交换误差，再使用等效旋转矢量计算姿态更新四元数，四元数表示简洁而且无奇异。等效旋转矢量多子样算法的理论基础是如下给出的Bortz方程[2]：

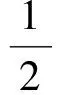
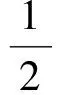
(1)

式中：φ(t)，ω(t)和Δθ(t)分别表示等效旋转矢量、角速度和角增量,上标×表示反对称阵。

传统基于泰勒级数展开的多子样算法推导，忽略了Bortz方程右端三阶项的影响，并将二阶项中的等效旋转矢量近似为角增量[3-5]。传统基于圆锥运动环境下的优化多子样算法，将锥角假设为小角度，理论上其在一个姿态更新周期内子样数越多精度越高[6-7]。但是，上述推导过程中所做的前提近似或假设，使得传统的算法精度往往达不到宣称的理想效果[8]，特别是在大角度机动或大锥角圆锥运动环境下，有时采用高子样算法的精度反而不如低子样的精度。文献[9]和[10]分别提出了显式频率整形和扩展圆锥误差补偿算法，对传统算法做了改进，在大机动情形下提高了误差补偿精度，然而它们也是仅考虑了圆锥误差二阶项的影响，大机动条件下依然无法避免原理性误差。作为传统方法的改进，文献[11]考虑了Bortz方程中三阶项的影响，提出了更高精度的误差补偿算法，但是其推导过程比较繁琐，仍然难以避免在大机动条件下产生误差。未来随着高精度5 m/h量级冷原子陀螺的使用，人们对导航计算精度要求必将越来越高，且随着高超声速飞行器和旋转弹等大机动领域的应用拓展，有必要研究更高精度的导航算法[10,12]。

传统的多子样算法推导的目标是获得一组确定的不可交换误差补偿系数，即角增量各子样之间叉乘的系数，子样数越多，推导过程就越复杂，为了公式推导可以顺利进行，需做必要的近似简化或假设，使得推导结果是近似或隐含适用条件的。本文摒弃了传统的求取确定性补偿系数的思路，在角速度函数为关于时间的多项式条件下(任何连续函数都能用多项式以任意给定的精度逼近)，根据四元数微分方程的毕卡级数解直接推导姿态更新的数值算法，其结果是以时间多项式为元素的变换四元数，在推导过程中无需做任何近似，精度仅仅取决于计算机的数值计算精度。新算法易于软件编程实现，通过对比仿真试验校验了新算法的高精度性能。

1 多项式角运动描述

在实际捷联惯导系统中，大多数陀螺采样直接获得的是角增量信息，而姿态毕卡更新算法需要用到角速度作为输入。因此，在角运动为多项式形式假设条件下先给出由角增量信息构造角速度的方法。

假设角速度ω(t)是关于时间t的N-1次多项式，即

(2)

假设陀螺采样间隔为h，在时间段(-ph,nh]内进行了N次角增量采样(p≥0,n>0且p+n=N)，分别记为Δθj(j=-p+1,-p+2,…,n)，对式(2)积分可得

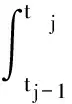
(3)

式中：简记tj=jh，当tj>0时表示当前姿态更新周期内的角增量采样；而当tj≤0时表示利用了前面姿态更新周期的角增量信息。

根据式(3)，将相继N次角增量合并在一起写成矩阵形式，如下所示

Θ=2WΓ

(4)

式中：

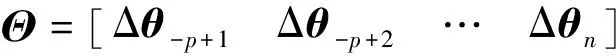
由式(4)容易求得以角增量表示的多项式系数矩阵

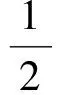
(5)

由此可见，根据相继的N次角增量采样，通过式(5)和式(2)总可以构造一个(N-1)次的多项式角速度拟合。

2 姿态四元数微分方程的毕卡级数解法

用四元数表示的姿态微分方程为[13]

(6)

(7)

若四元数初值Q(0)和角速度函数W(t)均已知，类似于矩阵微分方程的毕卡级数解[14]，不难求得四元数微分方程(7)的毕卡级数解为

Q(t)=Q(0)∘q(t,0)

(8)

(9)

式中：q(t,0)为从时间0到t的姿态变化四元数，完全由角速度决定。一般情况下无法再对式(9)作进一步处理;但是，如果假设角速度W(t)为关于时间t的多项式函数，则可得到q(t,0)的多项式积分解，具体分析如下所述。

首先，计算式(9)右端的单重积分项，将三维矢量表示为零标量四元数，得

(10)

其次，将式(10)代入式(9)右端的双重积分项，可得

(11)

根据如下两四元数P和Q之间的乘法运算规则

(12)

并且注意到两个以多项式为元素的四元数之乘积仍然是多项式四元数，式(11)转化为

(13)

式中：运算符“*”表示两个多项式系数行向量之间的卷积运算。

同理，将式(13)代入式(9)右端的三重积分项，得

(14)

至此，获得式(9)的幂级数解为

(15)

式(15)是关于时间t的无穷阶幂级数，但在实际应用中，总是选取式(15)的前低阶有限项作为姿态更新的数值解；容易看出，当保留前m阶时，数值截断误差为O(tm+1)。为了降低计算量，当选前m阶时，在所有保留的积分项中均可删去次数高于m的多项式系数，不影响截断误差的阶次。一般在姿态更新周期nh小于0.1s并且角速度多项式系数在数值上不超过10量级的情况下，可选择保留毕卡级数的前10～15阶作为精确的数值解。

特别地，若将姿态更新间隔nh作归一化处理，即令nh=1，则由式(15)可求得

(16)

进而式(5)中的W和Γ可转化为

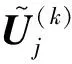
(17)

(18)

例如，当N=6，m=10时，乘法次数为3600；而当N=4，m=5时，乘法次数为600，通常也能取得比较满意的数值精度。

与本文算法的计算量相比，若采用如下传统的扩展形式不可交换误差补偿算法[6,10]

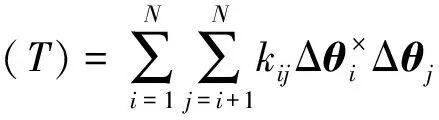
(19)

式中：δφ(T)和kij分别为圆锥误差积分和不可交换误差补偿系数。式(19)中含有N(N-1)/2次矢量叉乘运算和系数乘法运算，因此传统算法的乘法次数为

(20)

根据式(18)和式(20)，可获得本文算法与传统算法的计算量比率为

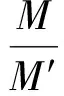
(21)

3 仿真与分析

3.1 圆锥运动仿真

圆锥运动仿真参数设置为：圆锥频率f=1 Hz，半锥角变化范围α=0.05″～90°，角增量采样间隔h=10 ms 。经过仿真，在圆锥轴上的姿态漂移误差ε如图1所示，实线为传统圆锥误差补偿算法的姿态漂移误差，点划线为本文所提新算法的误差，各图例依次对应子样数N=2～6(这里未采用前一姿态更新周期的角增量信息，即参数p=0)。从图1可以得出以下几点结论：

1)当子样为2时，两种算法误差曲线几乎重合，即两者精度相当。

2)新算法随子样数增加精度不断提高;2，3子样(或4，5子样)之间的精度相对来说比较接近。

3)对于传统算法，在半锥角很小时子样数越高精度才会越高，比如当半锥角小于1″时6子样的精度才高于5子样；而当半锥角较大时，传统算法的高子样算法精度反而不如低子样算法，特别在半锥角α= 90°时6子样算法的漂移误差高达20°/h。

4)在大半锥角情况下，新算法精度明显优于传统算法；而当半锥角较小时，新算法也具有足够高的精度，对于实际应用而言误差可忽略不计，总体上看，新算法受半锥角影响小，具有更强的实用性。

此外，仿真还显示，传统算法在非圆锥轴上的误差波动较大，而新算法误差均很小。不妨以半锥角α= 90°环境下的6子样算法为例，图2给出了两种算法在一个圆锥角运动周期内的非圆锥轴上的角度更新误差(δφx和δφy)比较。从图2可以看出，传统算法的误差最大达到了320″，而新算法的误差始终很小，仅为10-6″量级。这说明，如果出现非整周期的圆锥运动，传统算法可能会引起较大的姿态解算误差。

3.2 大角度机动仿真

实际上，第3.1节给出的短时低频大幅值圆锥运动也可以视为一种大角度机动类型。下面采用文献[9-10]中以多项式表示的2 s 大角度机动环境，重写多项式系数如下所示：

(22)

仿真时除采用传统圆锥误差补偿算法和本文新算法外，还增加了文献[10]提出的扩展圆锥补偿算法，但由于扩展算法的推导非常繁琐，尚未查找到6子样系数的公开文献，因而扩展算法最多只仿真到5子样。三种算法的角增量采样间隔均为h=10 ms，仿真结果的姿态漂移误差(δφx、δφy和δφz)如图3所示。由图3可得以下两点结论：

1)扩展算法3～5子样的精度明显优于传统圆锥算法，但是两者的算法精度都随着子样数的增加反而下降，传统算法N=6子样时x轴姿态漂移误差将近20″，见图(a 5)，扩展算法N=5子样时z轴漂移也超过了0.5″，见图(b 4)。

2)新算法的精度均高于传统算法和扩展算法，且新算法精度随子样数增加不断提高。事实上，式(22)为角速度的4次多项式描述，新算法的高于4子样的解式(15)可以认为是姿态更新的精确数值解或幂级数解析解，其精度仅受限于计算机的数值计算精度，正如新算法中图(c 4)和图(c 5)所示，它们的误差都非常小，几乎可忽略不计。

4 结 论

传统圆锥误差补偿算法在纯圆锥运动环境下且半锥角比较小时是非常有效的，然而对于大锥角情况或者应用于大角度机动环境，都会产生较大的姿态漂移误差。论文根据四元数微分方程的毕卡级数解，提出了一种新的直接求解姿态四元数更新的数值算法，在算法推导过程中不做任何近似处理，算法精度高，环境适应性好。通过与传统的基于等效旋转矢量的多子样算法对比仿真，校验了新算法在圆锥运动和大角度机动等场合均具有明显的精度优势，因而具有更好的应用价值。虽然新算法的计算量比传统算法稍大些，但是相对于当代高性能导航计算机的处理能力而言，还是容易满足实时计算要求的。在事后分析处理方面，新算法还可以作为研究其它姿态更新算法的精度比较参考基准。由于缺乏高精度的惯导系统、高动态环境模拟设备以及实时高精度的姿态参考基准，目前论文研究主要集中在理论分析和仿真对比层面上，希望所提出的理论和算法今后能在实际系统中得到进一步验证。

[1] Cheng H, Gupta K C. A historical note on finite rotations[J].Journal of Applied Mechanics, 1989, 56: 139-145.

[2] Bortz J E. A new mathematical formulation for strapdown inertial navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, 7(1): 61-66.

[3] Miller R. A new strapdown attitude algorithm[J]. Journal of Guidance, Control, and Dynamics, 1983, 6(4): 287-291.

[4] Lee J G, Yoon Y J, Mark J G, et al. Extension of strapdown attitude algorithm for high-frequency base motion[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(4): 738-743.

[5] 王立冬，孟亚峰，高庆. 基于角增量和角速率的旋转矢量算法的等效性[J]. 宇航学报, 2014, 35(3): 340-344.[Wang Li-dong, Meng Ya-feng, Gao Qing. Equivalence analysis of rotation vector algorithm based on angle increment and angular velocity[J]. Journal of Astronautics, 2014, 35(3): 340-344.]

[6] Ignagni M B. Efficient class of optimized coning compensation algorithms[J].Journal of Guidance, Control, and Dynamics, 1996, 19(2): 424-429.

[7] Park C G, Kim K J, Lee J G, et al. Formalized approach to obtaining optimal coefficients for coning algorithms[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(1): 165-168.

[8] 严恭敏,严卫生,徐德民. 经典圆锥误差补偿算法中剩余误差估计的局限性研究[J]. 中国惯性技术学报, 2008, 16(4): 379-385.[Yan Gong-min, Yan Wei-sheng, Xu De-min. Limitations of error estimation for classic coning compensation algorithm[J]. Journal of Chinese Inertial Technology, 2008, 16(4): 379-385.]

[9] Savage P G. Coning algorithm design by explicit frequency shaping[J].Journal of Guidance, Control, and Dynamics, 2010,33(4):1123-1132.

[10] 宋敏. 高动态下捷联惯性导航算法误差分析与优化方法研究[D]. 长沙：国防科学技术大学,2012.[Song Min. Research on error analysis and optimization methods for strapdown inertial navigation algorithm under highly dynamic environment [D]. Changsha: National University of Defense Technology, 2012.]

[11] Wang M S, Wu W Q, Wang J L, et al. High-order attitude compensation in coning and rotation coexisting environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 1178-1190.

[12] 朱常兴,冯焱颖,周兆英,等. 原子惯性技术在航天航空领域的应用[J]. 宇航学报,2009,30(1):18-24. [Zhu Chang-xing, Feng Yan-ying, Zhou Zhao-ying, et al. Applications of atom inertial technology in aerospace engineering [J]. Journal of Astronautics, 2009,30(1):18-24.]

[13] 秦永元. 惯性导航(第二版)[M]. 北京:科学出版社，2014: 253-255.

[14] 袁信,郑锷. 捷联式惯性导航原理[M]. 南京：航空专业教材编审组,1985: 54-55.

AnAccurateNumericalSolutionforStrapdownAttitudeAlgorithmBasedonPicardIteration

YAN Gong-min, WENG Jun, YANG Xiao-kang, QIN Yong-yuan

(School of Automation, Northwestern Polytechnical University, Xi’an 710072, China)

For strapdown attitude updating algorithm, in order to reach a high accuracy under a high attitude maneuver, a new numerical attitude algorithm is proposed based on the Picard series solution for the attitude quaternion differential equation. In this new algorithm, the angular velocity polynomial fit is obtained for the gyro angular increment, and the product of the polynomial quaternion is converted into the convolution operation of the angular velocity polynomial coefficients, then the Picard series solution is well settled. There exists no approximation or hypothesis in this deduction, which means the new algorithm is analytically accurate. Finally, under the large amplitude cone motion and high maneuver environment, some comparison tests both using the traditional algorithm and the new presented algorithm are carried out, and the results show the significant accuracy improvement in the new algorithm.

Strapdown attitude algorithm; Picard series; Polynomial fit; Simulation test

2017- 02- 23;

2017- 09- 21

航空科学基金(20165853041)

V249.3

A

1000-1328(2017)12- 1307- 07

10.3873/j.issn.1000- 1328.2017.12.007

严恭敏(1977-)，男，博士，副教授，主要从事惯性导航与信息融合理论方面的研究。

通信地址：陕西省西安市西北工业大学自动化学院183号信箱(710072)

电话：(029)88431369

E-mail: yangongmin@163.com