高超声速飞行器非线性自适应姿态控制
2018-01-04胡军
胡 军
(1. 北京控制工程研究所,北京 100094;2. 空间智能控制技术重点实验室,北京 100094)
高超声速飞行器非线性自适应姿态控制
胡 军1,2
(1. 北京控制工程研究所,北京 100094;2. 空间智能控制技术重点实验室,北京 100094)
分析了影响高超声速飞行器姿态运动的关键要素和不确定性,提出了包括动压关联输出变换、非线性黄金分割自适应控制律Ⅲ、积分器以及可选择的前馈控制在内的一种高超声速飞行器姿态控制新方案,解决了飞行过程中气动动压快速变化对姿态控制系统稳定性和控制精度影响的问题,提高了系统对关键参数不确定性如气动参数偏差、气动阻尼系数偏差、大气密度偏差、惯量偏差以及初始条件偏差的鲁棒性和适应性;所提方案用于高超声速飞行器再入过程高度、速度快速变化导致动压急剧变化的下压段的姿态控制系统设计中。仿真结果表明,在标称和多种偏差组合条件下,性能指标满足要求,控制量满足约束条件。
高超声速飞行器; 非线性;自适应控制;积分器;可选择的前馈控制器
0 引 言
速度大于5马赫的飞行器一般称为高超声速飞行器,其特点是速度快、机动性能强、飞行范围广,具有较短时间内的全球投送能力,亦可发展为可重复使用的空间运输工具以及国际间快速运输交通工具[1]。
由于高超声速飞行器动力学存在显著的非线性、时变和不确定性,非线性(含反馈线性化)控制[2]、滑模鲁棒控制[3]、自适应控制[4]、智能控制[5]等都用于高超声速控制的研究。近十年以来作者所在单位及国内有关单位在高超声速飞行器基于特征模型的自适应控制方面开展了持续的研究[6-12]。综观国内外高超声速飞行器控制系统的研究状况,文献很多,但距离解决工程实际问题的差距仍较大。主要表现在:对高超声速飞行器最具特色的高度、速度、动压急剧变化的飞行阶段研究得少,这是比平稳滑翔段难度更大的问题;在以气动为主的姿态控制设计与仿真中,考虑舵机物理约束的少,舵机的速率饱和对控制系统的设计有比幅值饱和更大的制约[13-14]。目前针对复杂快变对象且考虑舵机幅值与速率约束的研究相对很少。文献[15]利用滑模干扰观测器和引入韩氏非线性跟踪微分器的轨迹线性化方法,研究了高超声速飞行器滑翔段带幅值饱和与速率饱和的姿态控制问题。
针对高度、速度急剧变化的下压段或拉起段,由于作用在高超声速飞行器上的动压急剧变化,给控制器设计带来极大的难度。对自适应控制而言,传统的参数估计方法,控制误差作为参数估计的唯一驱动数据源,在对象参数快速变化的短时间内,仅以小的控制误差作为数据驱动源的参数估计理论不能适应参数的快速变化;文献[11]利用高度与动压相结合的经验公式补偿特征模型中控制输入系数的不确定性;文献[12]采用神经元网络方法,控制误差作为参数估计的数据驱动之一,结合物理特征,如高度、速度等,利用神经元网络以及事先在线训练与学习,获得恰当的参数初值以及任务中较好的参数估计,取得较好的控制效果。该方法对先验知识以及离线、在线学习的要求很高。两篇文献均采用了相同的控制器结构,即线性黄金分割自适应控制+逻辑积分+逻辑微分,文献[12]还利用参数估计结果计算控制量的给定部分,在控制器的设计上,两篇文献都采用了若干增益调度策略,设计与仿真研究中也都考虑了舵机的物理约束。
本文依据高超声速飞行器运动方程特性,从数学关系的角度,分析了按气动方式飞行的高超声速飞行器姿态控制系统的特点,据此设计了:(1)积分控制+可选择前馈,跟踪攻角、侧滑角配平状态;(2)动压相关变换+本文提出的非线性黄金分割自适应控制方法Ⅲ,作为反馈控制,跟踪攻角、侧滑角和倾侧角的目标值。应用(1)、(2),得到简单、鲁棒、自适应能力强的高超声速飞行器非线性自适应控制器,控制方法无逻辑或数值切换,应用于高超声速飞行器高度、速度急剧变化的下压段的姿态控制,取得良好控制性能,控制量满足舵机物理约束。本文为已知任务规划的快变对象控制系统的设计提供了一种实用方法。
1 高超声速飞行器运动方程
1.1 运动方程[1]
考虑气动力和地球自转,姿态运动学方程如下:
(1)
其中
(2)
姿态动力学方程如下:
(3)
弹道运动学方程:
(4)
弹道动力学方程:
(5)
符号说明:
α、β、γv:分别为攻角、侧滑角、倾侧角;
ωx、ωy、ωz:分别为滚动、偏航和俯仰角速度;
V、θT、σ:分别为相对地球的速度、弹道倾角、弹道偏角;
R、Φ、λ分别为飞行器质心的地心距、地心纬度、经度;ωie为地球自转角速度,g为地球引力加速度
D、L、Z:分别为飞行器受到的气动阻力加速度、升力加速度、侧向力加速度。
Ixx、Iyy、Izz为三轴转动惯量,
Ixy、Iyz、Ixz为惯量积,
Tx、Ty、Tz为三轴方向的总外力矩。
1.2 执行机构动力学
执行机构动力学模型描述了舵面偏转或舵机转动的动态特性,模型如下[11,12]:

(6)
额定状态下
τSF=0.002s,ωSF=90/s,ζSF=0.7
此外,舵面偏转还有角度、角速度限制。
左、右升降舵偏转角范围:
方向舵偏转角范围:-20°≤δ3°≤20°
升降舵、方向舵偏转角速度范围:
执行机构模型见图1。
三通道舵偏与三舵面舵偏的关系如下:
(7a)
(7b)
1.3 气动特性[11-12]
在机体系下,静态气动力包括轴向力Qx1、法向力Qy1、侧向力Qz1;静态气动力矩包括滚动力矩Mx1、偏航力矩My1、俯仰力矩Mz1,按下式计算:
(8a)
(8b)
式中CA、CN、CZ、Cl、Cn、Cm为轴向力系数、法向力系数、侧向力系数、滚转力矩系数、偏航力矩系数、俯仰力矩系数。
lt:飞行器参考长度;St:飞行器参考面积;q:动压,q=0.5ρV2。
静态气动参数是马赫数Ma、高度h、攻角α、侧滑角β、俯仰通道舵偏角δφ、偏航通道舵偏角δψ和滚动通道舵偏角δγ的函数。静态气动参数Ci(i=A、N、Z、l、m、n)按下式计算:
C(Ma,h,α,β,δφ,δψ,δγ)=C0(Ma,h,α,β)+
ΔCφ(Ma,h,α,β,δφ)+ΔCγ(Ma,h,α,β,δγ)+
ΔCψ(Ma,h,α,β,δψ)
(9)
在机体系下,气动阻尼力矩包括滚动阻尼力矩Mzn,x1、偏航阻尼力矩Mzn,y1、俯仰阻尼力矩Mzn,z1,按下式计算:
(10)
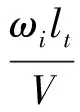
2 高超声速飞行器姿态控制设计
2.1 开环输入输出分析
对三个控制通道,进行开环输入输出分析。
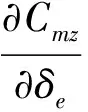
综上,开环输入输出总增益
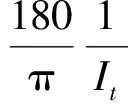
(11)
2.2 积分控制+可选择的前馈
上层任务(制导指令)给出的攻角不是自然配平状态,需要一定的升降舵偏来平衡(配平),升降舵标称平衡(配平)舵偏可以根据标称气动数据表获得,因此可采用前馈。
考虑实际质量特性、气动布局与设计状态偏差可能引起的姿态控制误差,引入积分控制,主要用于补偿实际飞行过程中气动系数偏差引起前馈输入偏离配平舵偏角的情况。
攻角通道、侧滑角通道引入积分控制,补偿因质心变化等引起舵偏配平状态的变化。由于积分控制本身也具有跟踪升降舵标称平衡(配平)舵偏的功能,前馈控制可根据数学仿真情况选择任务中是否引入。
2.3 与动压相关的输出变换
根据被控对象运动学、动力学和开环输入输出分析,设计与动压相关输出变换,补偿动压变化造成的舵偏角到气动力矩的控制增益变化。设计动压相关输出变换的形式如下:
(12)
其中,Q为动压,Qmax、Qmin分别为任务规划中的最大与最小动压,0.4≤μ≤1,ε=1.0×10-6,D1为保证稳定性与精度的设计参数。
推进长江水生态文明建设的实践与思考 …………… 洪一平(15.57)黄河流域水生态文明建设的探索与实践 …………… 司毅铭(15.60)
对下压段,Qmin为起始阶段动压、Qmax为终段动压,Q为过程中动压。起始阶段Q=Qmin,D(k)大,同样的误差与控制力矩需求,舵偏角大;终段Q=Qmax,D(k)小,同样的误差与控制力矩需求,舵偏角小;整个过程对Q的变化都有补偿作用。
式(12)同样适用拉起段、滑翔段。
2.4 自适应控制律
2.4.1参数估计
在文献[17-18]基础上,采用梯度投影算法进行参数估计。
定义回归向量:
φT(k)= [y(k-1),y(k-2),
(Δt)2u(k-1)]T
(13)
式中,Δt为控制周期。
θT(k)=[α1(k),α2(k),b0(k)]T
(14)
参数估计公式:
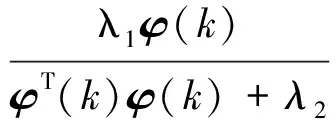
[y(k)-φT(k)θ(k-1)]
(15a)
θ(k)=π[θ*(k)]
(15b)
其中,π[x]表示x到有界闭集D上的正交投影,π[θ*(k)]将θ(k)投影到θ(k)的参数范围内。
2.4.2非线性黄金分割控制律Ⅲ
考察线性黄金分割控制律[16]、非线性黄金分割控制律Ⅰ[18]、非线性黄金分割控制律Ⅱ[19](注:Ⅰ、Ⅱ为本文作者自定义),经过多种误差组合的数学仿真研究和对结果的分析基础上,提出一种新的控制律,命名为非线性黄金分割控制律Ⅲ,公式如下:
u(k)= -[Kp(k,x(k))x(k)+Kd(k)
(x(k)-x(k-1))]
(16)
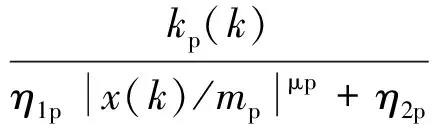
(17)
Kd(k,x(k))=kd(k)(η1dx(k)/mdμd+η2d)
(18)
(19)
(20)
(21)
记:
(22)
强制约束:
(23)
相对线性黄金分割控制律,非线性黄金分割控制律Ⅰ对比例控制部分进行了非线性调整,Ⅱ对差分控制部分进行了非线性调整,非线性黄金分割控制律Ⅲ对比例控制部分和差分控制部分同时进行了调整,比例控制系数随误差增大而非线性减小,差分控制系数随误差增大而非线性增大,当误差增大时,降低系统频带与增加系统阻尼并用,增大闭环系统惰性;与Ⅰ、Ⅱ不同,非线性黄金分割控制律Ⅲ在非线性部分对自变量除以mi,i=p,d, 取0 y(k+1)=α1(k)y(k)+α2(k) y(k-1)+b0(Δt)2u(k) (24) 式中,Δt是控制周期,α1(k)、α2(k)与运动方程系 数和控制周期相关,取值范围 (25) b0满足 b0∈[b0min,b0max] (26) 文献[16,18-19]分别证明了线性黄金分割控制律(式(16)~(23)当(17)式中Kp(k,x(k))=kp(k)、式(18)中Kd(k,x(k))=kd(k))、非线性黄金分割控制律Ⅰ(式(16)~(23)且当(18)式中Kd(k,x(k))=kd(k))、非线性黄金分割控制律Ⅱ(式(16)~(23)且当(17)式中Kp(k,x(k))=kp(k)),与二阶特征模型(24)~(26)组成的闭环系统以原点为平衡位置的渐近稳定性。由于非线性黄金分割控制律Ⅲ与前三个控制律相差的是一个乘性的非线性连续函数η1y(k)μ+η2,类似地有如下定理: 定理的证明与文献[19]类似,略。 采用三通道独立控制结构,图2为攻角通道姿态控制系统框图。 特别指出:系统参数辨识来自两个信息: (1)控制误差y=目标输入-被控对象输出 (测量与导航系统给出),控制误差y中含被控对象输出的信息; (2)非线性黄金分割自适应控制律的输出u。该输出u经过“与动压相关的动态变换”、“舵面分配”、“执行机构”后,变换为被控对象的实际输入。输出u中含有被控对象输入的信息。 从图2看出,将“与动压相关的动态变换”、“舵面分配”、“执行机构”与“被控对象”看成一体,作为“非线性黄金分割自适应控制律”的“广义对象”,则输出u是“广义对象”的输入。相对于原来“被控对象”与动压相关的大范围变化的时变动态控制增益,“广义对象”时变动态控制增益的变化范围大幅度减小,非常有利于系统参数辨识和自适应反馈控制的设计。 图2系统辨识的是误差y与反馈控制量u之间的模型,用二阶特征模型表示,见式(24),辨识公式见式(13)~(15),非线性黄金分割自适应控制律Ⅲ的计算公式见(16)~(23)。 攻角、侧滑角、倾侧角下压段初值偏差:±1.5°、±1.5°、±1.5;俯仰、偏航、滚动角速度初值偏差:±3.0°/s、±3.0°/s、±3.0°/s。 法/侧向力系数偏差:±15%;轴向力系数偏差:±20%;气动力矩系数偏差:±30%;气动阻尼力矩系数偏差:±50%;转动惯量数据偏差:±10%;大气密度:45 km高度以下取±15%,70 km高度以上取±30%,45 km~70 km高度按线性插值。此外还有影响所有气动系数的质心偏差,具体数据略。 阻尼系数取负边界。质心偏差、参数偏差以及初始状态偏差分三组,每组分别取正负边界,8种情况;记+1代表正向最大边界,-1代表负向最大边界。另取质心偏差(+1-1+1)、气动系数偏差(+1-1+1,-1+1-1)、大气密度偏差+1、惯量偏差(-1-1-1)、初始状态偏差(+1+1-1+1+1-1)组合。对上述工况再加上标称工况共计10种工况,分别进行控制结构有前馈和无前馈的数学仿真。采用(1)~(10)组成的包含攻角、侧滑角、倾侧角、三轴角速度、位置矢量和速度矢量的六自由度模型以及含有延迟、幅值约束和速率约束的执行机构模型。目标姿态角见图3。 10种工况的姿态误差见图4,下压段见图5。10种工况的姿态误差见图6,下压段见图7。从图4~图7中看出,控制结构有前馈和无前馈两种情况下,针对10种工况的仿真,误差结果是相当的,两种条件下的控制性能均满足要求。从细微看,两种条件下的控制性能相差无几,无前馈情况下的终点处个别工况下存在攻角的微幅振荡,有前馈情况下,终点处的稳定裕度相对更好些。前馈控制适用于舵面正常情况下;舵面有损坏的情况,则不能用前馈。 设计和仿真中考虑了舵机的幅值和速率约束,图8给出了10种工况无前馈情况下的舵偏角。从仿真结果看,控制系统方案应用动压相关输出变换、非线性自适应控制律Ⅲ、积分器以及可选择的前馈控制,能全面满足高超声速飞行器下压段姿态控制的要求。 针对影响高超声速飞行器姿态运动的关键要素和不确定性,提出了包括动压关联输出变换、非线性黄金分割自适应控制律Ⅲ、积分器以及可选择的前馈控制在内的一种高超声速飞行器姿态控制新方案,解决了飞行过程中气动动压快速变化对姿态控制系统稳定性和控制精度的影响,提高了对系统关键参数不确定性如气动参数偏差、气动阻尼系数偏差、大气密度偏差、惯量偏差以及初始条件偏差的鲁棒性和适应性;所提方案用于高超声速飞行器再入过程高度、速度快速变化导致动压急剧变化的下压段的姿态控制系统设计中。数学仿真结果表明,在标称和多种偏差组合条件下,性能指标满足要求,控制量满足约束条件。 [1] 李惠峰.高超声速飞行器制导与控制技术[M].北京:中国宇航出版社,2012. [2] Wallner E M, Well K H. Attitude control of a reentry vehicle with internal dynamics [J]. Journal of Guidance, control, and dynamics, 2003, 26(6):846-854. [3] Hall C E, Shtessel Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle [J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6):1315-1328. [4] 高道祥, 孙增圻, 罗熊, 等. 基于Backstepping的高超声速飞行器模糊自适应控制[J]. 控制理论与应用,2008, 25(1):805-810. [Gao Dao-xiang,Sun Zeng-qi,Luo Xiong,et al. Fuzzy adaptive control for hypersonic vehicle via Backstepping method[J]. Control Theory & Applications, 2008, 25(1):805-810.] [5] Xu H, Mirmirani M, Ioannou P A. Robust neural adaptive control of a hypersonic aircraft [C]. AIAA Guidance, Navigation and Control Conference and Exhibit, 11-14, August, 2003, Austin, Texas, U.S.A. [6] Meng B, Wu H X. Characteristic model based control of the X-34 reusable launch vehicle in its climbing phase [J]. Science in China Series F: Information Sciences, 2009, 52(11):2216-2225. [7] 龚宇莲,吴宏鑫. 基于特征模型的高超声速飞行器的自适应姿态控制[J]. 宇航学报, 2010, 31(9): 2122-2128. [Gong Yu-lian, Wu Hong-xin. Characteristic model-based adaptive attitude control for hypersonic vehicle[J]. Journal of Astronautics, 2010, 31(9): 2122-2128] [8] ZHang Z, Hu J. Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller [J]. Science in China Series F: Information Sciences, 2012, 55(10):2243-2256. [9] 孙琦,周军,林鹏.基于特征模型的高超声速飞行器鲁棒控制方法[J].飞行力学, 2011,29(1):46-49. [Sun Qi, Zhou Jun, Lin Peng. Robust adaptive controller design for a hypersonic vehicle based on characteristic model[J]. Flight Dynamics, 2011, 29(1):46-49. ] [10] 杜立夫,黄万伟,刘晓东,等.考虑特征模型的高超声速飞行器全通道自适应控制[J].宇航学报,2016, 37(6):711-719. [Du Li-fu, Huang Wan-Wei, Liu Xiao-dong, et al. Whole-channel adaptive control for hypersonic vehicle considering characteristic model [J]. Journal of Astronautics, 2016,37(6): 711-719.] [11] 黄煌.乘波式高超声速飞行器再入过程姿态控制的研究[R].中国空间技术研究院博士后研究工作报告,2013. [Huang Huang. The research of attitude control of hypersonic cruise vehicle during reentry[R]. Postdoctoral Research Report, Beijing Institute of Control Engineering, China Academy of Space Technology, 2013] [12] Chang Y F, Jiang T T. Adaptive control of hypersonic vehicles based on characteristic models with fuzzy neural network estimators [J].Aerospace Science and Technology, 2017, 68:475-485. [13] Garelli F, Camocardi P, Mantz R J.Variable structure strategy to avoid amplitude and rate saturation in pitch control of a wind turbine[J].International Journal of Hydrogen Energy, 2010, 35(11):5869-5875. [14] Nguyen T, Jabbari F. Output feedback controllers for disturbance attenuation with actuator amplitude and rate saturation[J].Automatica, 2000, 36(9):1339-1346 [15] 邵星灵, 王宏伦.基于SMDO-TLC的高超声速飞行器姿态控制[J].北京航空航天大学学报, 2014, 40(11):1568-1575. [Shao Xing-ling, Wang Hong-lun. Attitude control for hypersonic vehicle based on SMDO-TLC[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(11):1568-1575.] [16] 吴宏鑫, 胡军, 解永春. 基于特征模型的智能自适应控制[M]. 北京:中国科学技术出版社, 2009. [17] 姜甜甜. 几类非线性不确定性系统基于特征模型自适应控制的稳定性研究[R]. 北京:北京控制工程研究所,2015. [Jiang Tian-tian. The stability study of some kinds of nonlinear uncertain systems based on characteristic model adaptive control[R]. Postdoctoral Research Report, Beijing Institute of Control Engineering, China Academy of Space Technology, 2015.] [18] 吴宏鑫, 王颖, 解永春. 非线性黄金分割自适应控制[J], 宇航学报, 2002, 23(6):1-8. [Wu Hong-xin, Wang Ying, Xie Yong-chun. Nonlinear golden-section adaptive control[J]. Journal of Astronautjcs, 2002, 23(6), 1-8.] [19] Yang J C, Hu J, Ni M L. Adaptive guidance law design based on characteristic model for reentry vehicles [J]. Science in China Series F: Information Sciences, 2008, 51(12), 2005-2021. TheNonlinearAdaptiveAttitudeControlforHypersonicVehicle HU Jun1,2 (1. Beijing Institute of Control Engineering, Beijing 100094, China;2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100094, China) The key factors and uncertainties that affect the attitude movement of a hypersonic vehicle are analyged and a new scheme of hypersonic vehicle attitude control is proposed, including pressure correlation output transformation, nonlinear golden section adaptive control law Ⅲ, integrator and optional feedforward control. The new scheme solves the influence of the rapid change of aerodynamic pressure on the stability and control precision of the attitude control system during flight, and improves the robustness and adaptability of the critical parameters of the system such as aerodynamic parameter deviation, aerodynamic damping coefficient deviation, atmospheric density deviation, inertia deviation and initial conditional deviation. The new scheme is applied to the attitude control of the dive phase of a hypersonic vehicle with the rapid variance of altitude and velocity, resulting in sharp variance of dynamic pressure. The mathematical simulation shows that the performance index satisfies the requirement and the control output satisfies the restriction. Hypersonic vehicle; Nonlinear; Adaptive control; Integrator; Optional feed-forward controller 2017- 07- 17; 2017- 10- 09 国家自然科学基金(61333008) TP273 A 1000-1328(2017)12- 1281- 08 10.3873/j.issn.1000- 1328.2017.12.004 胡军(1963-),男,博士,研究员,主要从事航天器制导导航与控制系统设计工作,以及智能自适应控制的理论研究与应用工作。 通信地址:北京市海淀区友谊路104号5142信箱151分箱(100094) 电话:(010)68111437 E-mail: hujunbice@126.com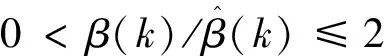
2.5 姿态控制系统结构
3 仿真校验
3.1 仿真条件
3.2 仿真结果
4 结 论
