求解轨迹优化问题的局部配点法的稀疏性研究

赵吉松

(南京航空航天大学航天学院，南京 210016)

求解轨迹优化问题的局部配点法的稀疏性研究

赵吉松

(南京航空航天大学航天学院，南京 210016)

直接配点法通过对控制变量和状态变量都进行离散将轨迹优化问题转化为非线性规划(NLP)问题。为了提高NLP的求解效率，需要利用其偏导数的稀疏特性并建立偏导数的高效计算方法。本文研究了局部配点法离散得到的NLP的一阶偏导数的稀疏特性，建立了一阶偏导数的高效计算方法。推导了NLP的目标函数梯度和约束雅克比矩阵的数学表达式，得到了NLP偏导数的稀疏型，并且将NLP的偏导数分解为原始轨迹优化问题的偏导数。由于原始轨迹优化问题的约束和变量的数量远少于NLP的约束和变量的数量，从而显著减小了NLP的一阶偏导数的计算量。含有离散气动力和推力数据的仿真算例验证了本文方法的有效性。仿真结果表明，与有限差分法直接计算NLP的偏导数相比，本文方法能够将优化耗时减小至4%以内，随着离散节点数目的增加，计算效率的提升更为显著。

轨迹优化；局部配点法；非线性规划；一阶偏导数；稀疏特性

0 引 言

轨迹优化对于飞行器设计有着十分重要的意义和工程实际价值[1]。轨迹优化本质上属于最优控制问题，其求解方法主要分为间接法和直接法。其中，直接法中的配点法通过对控制变量和状态变量进行离散将轨迹优化问题转化为非线性规划(NLP)问题，降低了对初值的敏感性并且具有很好的收敛性，近年来得到广泛的研究和应用[2-7]。

虽然配点法具有多方面优势，但是其具体实施方法对于提高优化效率具有重要影响。目前，以序列二次规划(SQP)为代表的基于梯度算法的NLP求解器需要提供NLP的目标函数和约束的一阶偏导数，甚至二阶偏导数。其中，一阶偏导数NLP求解器需要提供一阶偏导数，然后采用拟牛顿法(DFP法或者BFGS法等)构造近似的二阶偏导数，比如SNOPT[8]；二阶偏导数NLP求解器除了需要一阶偏导数，还需要准确的二阶偏导数，比如IPOPT[9]。但是，偏导数的计算量通常比较大，甚至超过优化算法本身。因此，提高NLP的一阶/二阶偏导数的计算效率对于提高轨迹优化效率有重要意义。

研究发现，由轨迹优化离散得到的NLP是非常稀疏的，即NLP的一阶偏导数和二阶偏导数含有大量零元素[2,10-12]。Betts等[10]较早地研究了局部配点法的稀疏特性，得到了梯形格式、Hermite-Simpson格式和Runge-Kutta格式的状态方程离散残差约束的偏导数的稀疏型，并将其中的非零元素转化为最优控制问题的偏导数，有效地减小了计算量。但是，Betts等[10]的研究存在一些不足之处：一是只给出了状态方程离散残差约束的偏导数稀疏特性和非零元素的计算方法，没有给出目标函数、路径约束和端点约束的偏导数的稀疏型和计算方法；二是对于最常用的Hermite-Simpson格式，没有完全探索出紧凑形式的状态方程离散残差的偏导数的稀疏型，而是通过在离散节点中间位置添加离散格式约束和状态变量将其转换为分离形式才得到完全的稀疏型。在Betts等的研究工作的基础上，Patterson等[11]研究了Radau伪谱法的一阶和二阶偏导数的稀疏性，得到了完整的稀疏型，并且推导出非零元素的高效计算方法(将NLP偏导数分解为最优控制问题的偏导数)。因此，如果能够基于上述研究，完全探索出局部配点法的NLP偏导数的稀疏型并建立偏导数的高效计算方法，对于提高局部配点法的优化效率具有重要意义。此外，与全局配点法(又称伪谱法，离散节点是正交多项式的根)相比，局部配点法的离散节点可以根据需要任意布置，在网格细化方面具有更好的灵活性[13-19]，适合求解非光滑轨迹优化问题。因而，提高局部配点法的优化效率还有能够促进局部配点法在非光滑轨迹优化领域的应用。

在实际应用中，一阶偏导数NLP求解器比二阶偏导数NLP求解器更为常用，因为二阶偏导数的计算通常比较繁琐并且计算量较大。以NLP的一阶偏导数为例，其计算方法可分为两大类。一类方法是直接计算NLP的偏导数，包括自动微分法[20]、复变量微分法[21]、有限差分法等。其中自动微分法计算量小，精度高，得到了广泛应用，其局限性在于要求优化模型解析可导，不适用于带有离散数据的轨迹优化问题。对于带有离散数据的优化模型，只能采用有限差分法。但是，采用有限差分直接计算NLP偏导数的效率较低，需要耗费大量的机时。另一类方法是将NLP的偏导数分解为最优控制问题的偏导数，然后采用各种微分算法计算最优控制问题的偏导数，并组装得到NLP的偏导数。因为与NLP相比，最优控制的约束和变量的数量大幅减少，因而这样处理可以显著提高偏导数的计算效率。

本文在Betts等[10]和Patterson等[11]的研究工作的基础上，以Hermite-Simpson格式为例，研究了局部配点法离散得到的NLP的一阶偏导数(目标函数梯度和约束雅克比矩阵)的稀疏性，建立非零元素的高效计算方法。采用带有离散参数模型的优化算例验证了所述方法的有效性。仿真结果表明，与采用有限差分法直接计算NLP的偏导数相比，本文方法能够将优化耗时减小至4%以下，并且随着离散节点数量的增加，计算效率的提升更为显著。

1 轨迹优化问题数学描述

轨迹优化问题本质上属于最优控制问题，以Bolza型最优控制问题为例，可描述为：求解控制变量u(t)∈Rm，使得如下目标函数最小化

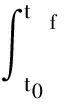
(1)

式中:M:Rn×R×Rn×R→R,L:Rn×Rm×R→R,x∈Rn,u∈Rm,t∈[t0,tf]⊆R。

状态方程为

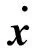
(2)

端点条件为

E(x(t0),t0,x(tf),tf)=0

(3)

路径约束为

C(x(t),u(t),t)≤0,t∈[t0,tf]

(4)

式中f:Rn×Rm×R→Rn,E:Rn×R×Rm×R→Re,1:Rn×Rm×R→Rc。方程(1)-(4)所描述的问题称为连续Bolza型最优控制问题。

2 基于Runge-Kutta格式的配点法离散

首先利用积分变换τ=(t-t0)/(tf-t0)将轨迹优化问题(方程(1)-(4))变换至时间区间τ([0,1]。假设单位区间[0,1]上的N个离散区间的节点为

τN=τf=1;τi<τi+1,i=0,1,…,N-1}

(5)

式中τi称为节点或网格点，τi在[0, 1]上可以均匀分布，也可以非均匀分布。

记xi=x(τi),ui=u(τi), 对于状态方程，基于q阶Runge-Kutta(RK)方法的离散格式为

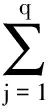
(6)

式中：Δt=tf-t0,hi=τi+1-τi,fij=f(xij,uij,τij;t0,tf),xij,uij和τij为中间变量，xij由下式给出

(7)

式中：τij=τi+hiρj,uij=u(τij).ρj,βj,αjl均为已知常数并且满足0≤ρ1≤ρ2≤…≤ρq≤1。当αjl=0(l≥j)时，离散格式为显式格式，否则为隐式格式。采用类似的方法，可将目标函数可离散化。常用的离散格式包括梯形格式(q=2)，Hermite-Simpson格式(q=3)，以及经典四阶Runge-Kutta格式(q=4)。

(8)

并且满足如下约束

(9)

Ci=C(xi,ui,τi;t0,tf)≤0

(10)

(11)

E(x0,t0,xf,tf)=0

(12)

式中

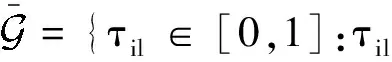
常用的离散格式有梯形格式(q= 2)，Hermite- Simpson格式(q= 3，简记HS格式)，以及经典四阶Runge-Kutta格式(q= 4，简记RK格式)。

以HS格式为例，该格式需要用到区间中点的变量和函数值，为此将区间中点的控制变量作为优化变量，并且在区间中点添加路径约束，即

(13)

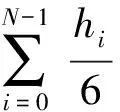
(14)

约束条件为

(15)

Ci=C(xi,ui,τi;t0,tf)≤0

(16)

(17)

E(x0,t0,xf,tf)=0

(18)

其中

在数值优化时，为了使问题具有实际物理意义，还需要添加时间差约束

Δt=tf-t0>0

(19)

3 NLP偏导数计算方法

3.1 依赖关系矩阵

在推导NLP一阶偏导数的稀疏特性时，需要用到原始轨迹优化问题对自变量的依赖关系。

由于状态方程、路径约束和目标函数Lagrange积分项都定义在整个时域区间，因而本文将这三项对自变量的偏导数定义在一起，

(20)

其中G1的每一项仍为矩阵，以∂f/∂xT为例，

(21)

易知，G1为(n+c+1)×(n+m+1)维矩阵。

通常情况下，G1是稀疏矩阵。为了描述G1的稀疏型，定义如下struct函数

(22)

记

S1=struct(G1)

(23)

式中struct (G1)表示对G1的每个元素进行struct运算。S1表示G1的稀疏型。为了得到S1，不需要计算G1的每个元素的具体值，只需要判断是否为0。

类似可以定义端点约束和目标函数的Mayer项对自变量的依赖关系矩阵和稀疏型

(24)

S2=struct(G2)

(25)

易知，G2为(e+1)×2(n+1)维矩阵。

3.2 变量记法

前述离散格式将同一个节点处的变量或约束记为一个列向量，这种记法与数值积分格式的形式一致，但是不利于推导偏导数矩阵的稀疏特性。为此，本文定义一种新的变量记法，将变量或约束的同一个分量在不同节点的值记为一个新的向量。

以状态方程离散残差为例，定义

ξ:,j=(ξ0,j,ξ1,j,…,ξN-1,j)T, (j=1,2,…,n)

(26)

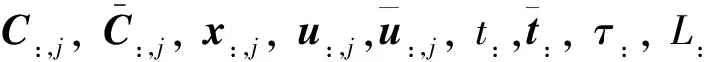
J(z)

(27)

并且满足约束条件

Fmin≤F(z)≤Fmax

(28)

式中：目标函数J(z)的表达式参见方程，优化变量z和约束函数F(z)的定义如下

(29)

3.3 目标函数梯度

目标函数梯度是指目标函数对优化变量的偏导数，具体定义如下

(30)

将目标函数写成矩阵乘积形式可得到

(31)

(32)

对角阵h=diag(h0,h1,…,hN-1)，其中hi(i=0, 1, …,N-1)为积分步长，矩阵D1和D2定义如下

D1和D2均为N×(N+1)矩阵，其中空白元素为0。

(33)

式中

可见，NLP的目标函数梯度可以分解为轨迹优化问题的目标函数和状态方程的偏导数。

3.4 雅克比矩阵

NLP的雅克比矩阵定义为NLP的约束对优化变量的偏导数矩阵，对于HS格式，形式如下

(34)

式中向量F和z的定义参见方程(29)。雅克比矩阵GF的展开形式遵循向量求偏导数运算规则(参见方程(21))。下文推导GF的数学表达式。

3.4.1状态方程离散残差约束的偏导数

结合前述定义的变量记法，将状态方程离散残差约束即方程写成如下形式

(35)

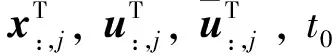
(36)

式中

3.4.2路径约束的偏导数

(37)

(38)

3.4.3端点约束的偏导数

(39)

3.4.4时间差约束的偏导数

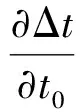
(40)

可见，NLP的雅克比矩阵可分解为轨迹优化问题的状态方程、路径约束、端点约束和时间约束的偏导数。计算出这些约束在离散节点和区间中点的偏导数(对于f和C)以及端点处的偏导数(对于E和Δt)之后，采用本节的方法组装得到雅克比矩阵。对于HS格式，以N=4为例，其雅克比矩阵的稀疏型如图1所示。其中，空白元素表示恒为零，“·”表示非零元素，“×”表示可能不为零的元素。

(41)

4 仿真算例

飞行器最短时间爬升问题最初由Bryson等[22]提出，此后得到广泛研究[2]。该算例的特色之处是推力和气动力数据以离散表格形式给出，与实际工程问题比较接近。基本问题是求解最优攻角α(t)，使得飞行器从跑道起飞爬升至指定高度消耗的时间最短。在纵向平面内，飞行器的运动方程组为[22]

(42)

式中h为高度，v为速度，γ为航迹角，m为质量，μ为引力常数，Re为地球半径。发动机推力T(Ma,h)由表 1给出(缺少的数据实际飞行不会用到)，Isp=1600 s，g0=9.80665 m/s2。气动力由下式给出[22]

式中L为升力，D为阻力，CL为升力系数，CD为阻力系数，S为参考面积，ρ为大气密度。气动力的相关参数CLα，CD0和η由表 2给出。

初始条件是h(t0)=0 m,v(t0)=129.314 m/s,γ(t0)=0°,m(t0)=19050.864 kg；终端约束是h(tf)=19994.88 m,v(tf)= 295.092 m/s,γ(tf)= 0°。

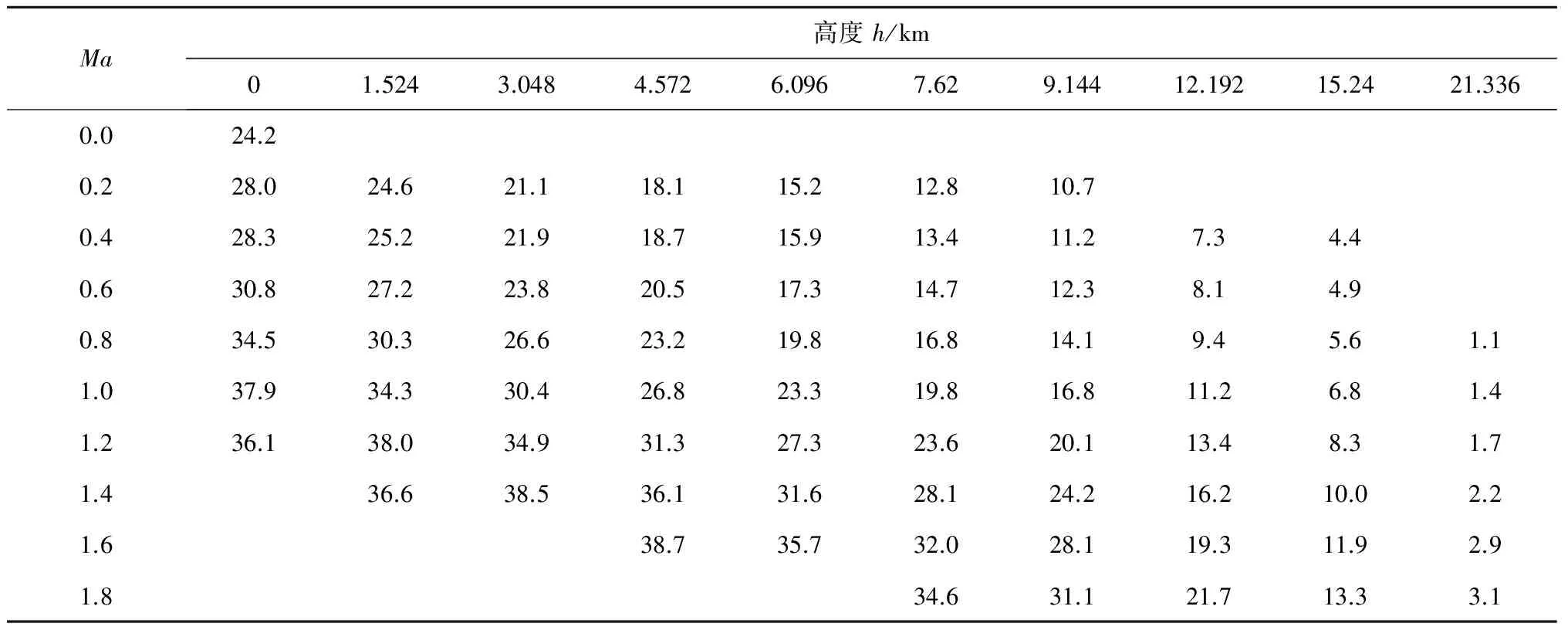
Ma高度h/km01．5243．0484．5726．0967．629．14412．19215．2421．3360．024．20．228．024．621．118．115．212．810．70．428．325．221．918．715．913．411．27．34．40．630．827．223．820．517．314．712．38．14．90．834．530．326．623．219．816．814．19．45．61．11．037．934．330．426．823．319．816．811．26．81．41．236．138．034．931．327．323．620．113．48．31．71．436．638．536．131．628．124．216．210．02．21．638．735．732．028．119．311．92．91．834．631．121．713．33．1

表2 气动力数据Table 2 Aerodynamic data

目标函数为飞行器爬升消耗的时间最短，即

J=tf

(43)

本算例的特点是推力数据和气动力数据是离散形式，并且推力数据不完整。文献[2]通过对推力数据进行最小曲率样条拟合，得到了完整、光滑的曲面，但是处理过程比较复杂，难以通用。本文采用线性外插法将表1中的推力数据补充完整，采用三次样条插值计算飞行过程的推力和气动力参数。大气模型采用美国1976 年标准大气进行插值。

采用局部配点法将该轨迹优化问题转化为NLP问题，采用SNOPT 7[8]求解NLP问题。对NLP一阶偏导数的两种计算方案进行了研究。一种方案是不提供NLP的一阶偏导数，此时SNOPT内部采用有限差分法直接计算NLP的偏导数。另一种方案即本文方法，采用有限差分法计算原始轨迹优化问题的一阶偏导数，采用第3节给出的方法组装得到NLP的一阶偏导数矩阵并提供给SNOPT。采用Matlab 2009a语言编程，表 3给出采用32、64和128个均匀离散节点时两种方案的优化效率对比。采用的计算机为MacBook Air(处理器Intel Core i5-5250U 1.6 GHz，操作系统Windows 10企业版，内存4 GB 1600 MHz DDR3)，计算耗时为10次运行的平均耗时。从表 3可以看出，与采用有限差分法直接计算NLP的偏导数相比，本文方法能够将计算耗时减小到4%以下，并且随着离散节点数目的增加，本文方法的优化效率提升更为显著。这是因为随着离散节点数量增加，NLP一阶偏导数矩阵具有更大的稀疏度(稀疏度定义为NLP的一阶偏导数矩阵中的零元素数量所占的比例)，参见表 3。

本算例的最优飞行攻角在部分区域变化比较剧烈。为了高精度捕捉最优攻角，本文将前述建立的偏导数高效计算方法与作者最近发展的网格细化技术[16]相结合求解该问题，优化结果如图 2和图 3所示。图中的圆圈为离散最优解，实线为基本无振荡插值(ENO)结果(对于控制变量)或者数值积分结果(对于状态变量)。网格细化算法迭代6次，从641个均匀离散节点中选取82个节点求解该问题，总耗时29.2 s，优化的最短爬升时间J* = 320.25 s。文献[2]的优化结果为324.98 s，二者差异主要是由采用的大气模型不同和对推力数据的处理方式不同造成的。文献[18]同样采用局部配点法和网格细化技术求解该问题，但是采用了有限差分法直接计算NLP的偏导数，优化耗时长达12.1分钟(CPU频率2.59 GHZ)。可见，本文方法与网格细化技术相结合，能够快速、高精度地求解轨迹优化问题。

表3 两种方法计算NLP偏导数的优化效率对比Table 3 Efficiency comparison of two derivative methods

5 结 论

本文以HS格式为例，研究了局部配点离散得到的NLP问题的稀疏特性，推导出NLP一阶偏导数的高效计算方法。首先引入一种新的变量记法将NLP问题写成向量形式，然后应用向量链式求导规则将NLP的偏导数转化为原始轨迹优化问题的偏导数。由于与NLP相比，轨迹优化问题的约束和自变量的数量大幅度减少，因而这样处理可以显著减小NLP的一阶偏导数的计算量。采用带有离散推力数据和气动力数据的仿真算例验证了本文方法的有效性。仿真结果表明，与采用有限差分法直接计算NLP的偏导数相比，采用本文方法能够大幅度减小优化耗时(对于算例，减小至4%以下)，并且随着离散节点数量的增加，本文方法计算效率的提升更为显著。虽然本文的研究工作基于HS格式，但是所给出的方法可容易推广至局部配点法的其它离散格式，比如梯形格式，经典四阶RK格式等。

[1] 唐国金, 罗亚中, 雍恩米. 航天器轨迹优化理论、方法及应用 [M]. 北京: 科学出版社, 2012.

[2] Betts J T. Practical methods for optimal control and estimation using nonlinear programming, advances in design and control series [M]. Philadelphia: Soc. for Industrial and Applied Mathematics, 2009.

[3] Fahroo F, Ross I M. Direct trajectory optimization by a Chebyshev pseudospectral method [J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 160-166.

[4] Benson, David. A Gauss pseudospectral transcription for optimal control [D]. Cambridge: Massachusetts Institute of Technology, 2005.

[5] 雍恩米, 唐国金, 陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化 [J]. 宇航学报, 2008, 29(6): 1766-1772. [Yong En-mi, Tang Guo-jin , Chen Lei. Rapid trajectory optimization for hypersonic reentry vehicle via Gauss pseudospectral method [J]. Journal of Astronautics, 2008, 29(6): 1766-1772.]

[6] 丁洪波, 曹渊, 佟卫平, 等. 亚轨道飞行器上升段轨迹优化与快速重规划 [J]. 宇航学报, 2009, 30(3): 877-883. [Ding Hong-bo, Cao Yuan, Tong Wei-ping, et al. Ascent trajectory optimization and fast-reconstruction for suborbital launch vehicle [J]. Journal of Astronautics, 2009, 30(3): 877-883.]

[7] 钟睿, 徐世杰. 基于直接配点法的绳系卫星系统变轨控制 [J]. 航空学报, 2010, 31(3): 572-578. [Zhong Rui, Xu Shi-jie. Orbit-transfer control for TSS using direct collocation method [J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(3): 572-578.]

[8] Gill P E, Murray W, Saunders M A. SNOPT: An SQP algorithm for large-scale constrained optimization [J]. Siam Journal on Optimization, 2002, 12(4): 979-1006.

[9] Biegler L T, Zavala V M. Large-scale nonlinear programming using IPOPT: An integrating framework for enterprise-wide dynamic optimization [J]. Computers & Chemical Engineering, 2009, 33(3): 575-582.

[10] Betts J T, Huffman W P. Exploiting sparsity in the direct transcription method for optimal control [J]. Computational Optimization & Applications, 1999, 14(2): 179-201.

[11] Patterson M A, Rao A V. Exploiting sparsity in direct collocation pseudospectral methods for solving optimal control problems [J]. Journal of Spacecraft and Rockets, 2012, 49(2): 364-377.

[12] 童科伟, 周建平, 何麟书. 稀疏拟谱最优控制法求解Goddard火箭问题 [J]. 固体火箭技术, 2009, 32(4): 360-364. [Tong Ke-wei, Zhou Jian-ping, He Lin-shu. Sparse pseudospectral optimal control method for solving Goddard rocket problem. Journal of Solid Rocket Technology, 2009, 32(4): 360-364.]

[13] Betts J T, Huffman W P. Mesh refinement in direct transcription methods for optimal control [J]. Optimal Control Applications and Methods, 1998, 19(1): 1-21.

[14] Jain S, Tsiotras P. Trajectory optimization using multiresolution techniques [J]. Journal of Guidance Control and Dynamics, 2008, 31(5): 1424-1436.

[15] Zhao Y, Tsiotras P. Density functions for mesh refinement in numerical optimal control [J]. Journal of Guidance Control and Dynamics, 2011, 34(1): 271-277.

[16] Zhao J, Li S. Modified multiresolution technique for mesh refinement in numerical optimal control [J]. Journal of Guidance, Control, and Dynamics, 2017, Online: https://arc.aiaa.org/doi/10.2514/1.G002796.

[17] 陈小庆, 侯中喜, 刘建霞. 基于多分辨率技术的滑翔飞行器轨迹优化算法 [J]. 宇航学报, 2010, 08): 1944-1950. [Chen Xiao-qing, Hou Zhong-xi, Liu Jian-xia. A multiresolution technique-based gliding vehicle trajectory optimization algorithm [J]. Journal of Astronautics, 2010, 31(8): 1944-195.]

[18] 赵吉松, 谷良贤, 佘文学. 配点法和网格细化技术用于非光滑轨迹优化 [J]. 宇航学报, 2013, 34(11): 1442-1450. [Zhao Ji-song, Gu Liang-xian, She Wen-xue. Application of local collocation method and mesh refinement to nonsmooth trajectory optimization [J]. Journal of Astronautics, 2013, 34(11): 1442-1450. ]

[19] 张松, 侯明善. 轨迹优化的LASSO网格自适应加密方法 [J]. 系统工程与电子技术, 2016, 38(5): 1195-1200. [Zhang Song, Hou Ming-shan. LASSO-based node adaptive refinement in trajectory optimization [J]. System Engineering and Electronics, 2016, 38(5): 1195-1200.]

[20] Csendes T. Developments in Reliable Computing [M]. Dordrecht: Kluwer Academic Publishers, 1999, 77-104.

[21] Squire W, Trapp G. Using complex variables to estimate derivatives of real functions [J]. SIAM Review, 1998, 40(1): 110-112.

[22] Bryson J A E, Desai M N, Hoffman W C. Energy-state approximation in performance optimization of supersonic aircraft [J]. Journal of Aircraft, 1969, 6(6): 481-488.

ExploitingSparsityinLocalCollocationMethodsforSolvingTrajectoryOptimizationProblems

ZHAO Ji-song

(College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

In a direct local collocation method, a trajectory optimization problem is transcribed into a nonlinear programming (NLP) problem. Solving this NLP as efficiently as possible requires that the sparsity of the NLP derivatives should be exploited and the derivatives should be efficiently calculated. In this paper, a computational efficient method is developed for computing the first derivatives of the NLP functions arising from a local discretization of a trajectory optimization problem. Specifically, the expressions are derived for the NLP objective function gradient and constraint Jacobian. It is shown that the NLP derivatives can be reduced to the first derivatives of the functions in the trajectory optimization problem. As a result, the method derived in this paper reduces significantly the amount of computation required to obtain the first-derivatives required by a NLP solver. The approach derived in this paper is demonstrated by an example with discrete aerodynamic data and thrust data where it is forund that the time required to solve the NLP is reduced to less than 4% compared with the direct differentiation of the NLP functions using a finite difference method, and the efficiency improvement is more significant as the number of the grid points increases.

Trajectory optimization; Local collocation method; NLP; First derivatives; Sparsity

2017- 07- 06;

2017- 10- 10

国家自然科学基金(11602107)；中国博士后科学基金(一等资助，168884)

V412

A

1000-1328(2017)12- 1263- 10

10.3873/j.issn.1000- 1328.2017.12.002

赵吉松(1984-)，男，博士，南京航空航天大学航天学院讲师，主要从事飞行器总体设计与轨迹优化等方面的研究。

通信地址：南京市秦淮区御道街29号(210016)

电话：18260412336

E-mail: zhaojisongjinling@163.com