多变量数据缺失机制的识别方法*
2018-01-03邱建青杜春霖李晓松
邱建青 杜春霖 周 婷 张 韬 李晓松
四川大学华西公共卫生学院(华西第四医院)(610041)
·综述·
多变量数据缺失机制的识别方法*
邱建青 杜春霖 周 婷 张 韬△李晓松△
四川大学华西公共卫生学院(华西第四医院)(610041)
数据缺失广泛存在于医学科研中,使研究损失大量信息,导致研究结果发生偏倚,因此不应该被忽略。缺失数据的处理方法较为成熟,但是这些处理方法都以特定的数据缺失机制为前提。
数据缺失机制的概念由Rubin于1967年提出[1],它描述了数据的缺失概率与观测到的变量和未观测到的变量之间的关系,说明数据缺失的原因。数据的缺失机制包括完全随机缺失(missing completely at random,MCAR)、随机缺失(missing at random,MAR)和非随机缺失(missing not at random,MNAR)三类。完全随机缺失是指目标变量的缺失概率与已观测到的变量和未观测到的变量无关,即缺失是完全随机发生的。随机缺失是指目标变量的缺失概率与已经观测到的变量相关,但与未观测到的变量无关。非随机缺失是指目标变量出现缺失的概率与未观测到的变量相关。
数据的缺失机制说明了数据缺失的原因,数据缺失的不同处理方法对应特定的缺失机制。研究发现[2-3],不根据缺失机制盲目选择处理方法的结果往往会有偏倚,所以,缺失机制的识别很重要。我们只有清楚数据的缺失机制,才能选择正确的方法。
目前针对单变量数据缺失机制识别的研究较为成熟,而关于多变量数据缺失机制识别的研究有所成果,但缺乏一个完整体系,本文将主要从数理方法角度入手,总结目前国外针对多变量缺失机制识别的各类方法,形成体系,以供借鉴。
资料与方法
检索方法:采用主题词结合关键词的方法,结合文献追溯及手工检索,以“missing data mechanism”、“MCAR”、“MAR”、“MNAR”为关键词检索Pubmed数据库;以“数据缺失机制”及“完全随机缺失”、“随机缺失”、“非随机缺失”为关键词检索中国生物医学、知网、维普和万方科技文献数据库。检索范围不限,并进一步查阅相关文献的参考文献来检索可能遗漏的文献。
文献纳入标准:纳入的文献必须具备以下条件:①缺失类型为多变量缺失;②缺失机制的分类为完全随机缺失、随机缺失和非随机缺失;③检验方法为原创。详见图1。

图1 文献检索纳入排除流程图
机制识别策略
按照三种机制的假定性强弱,我们按照零假设为MCAR、MAR、MNAR的顺序依次进行假设检验,检验顺序如图2示。各缺失机制的检验方法如下所述。

图2 多变量数据缺失机制识别方法选择步骤
1.多变量数据MCAR机制的识别方法
目前,大部分针对多变量数据的MCAR机制识别方法主要是通过将观测对象按照变量的缺失模式(missing pattern)分组,即将含有相同缺失变量的观测对象划分为同一组(如第一个观测对象和第五个观测对象都是变量3和变量4发生了缺失,这两个对象属于同一个缺失模式组);然后通过假设检验比较各组的均向量和(或)协方差矩阵是否相同。如果差异无统计学意义,则尚不能拒绝缺失机制是MCAR;如果各组间的差异有统计学意义,则可以认为该数据的缺失机制并非MCAR。而假设检验需综合考虑总体分布类型是否已知、是否分类变量、样本含量大小等情况选择适当的方法(图2)。
(1)参数检验
多重t检验:Dixon按每一个变量是否缺失将数据集划分为该变量缺失的数据集和未缺失的数据集,然后对每一对数据集中其他每个变量间进行两样本t检验[4]。该检验数理基础较为简单,但忽略了多变量数据中变量之间的关系,大量t检验也会增大Ⅰ型错误。
似然比检验:该方法由Little提出,基本思想是比较各个缺失模式组的均向量是否相同[5]。如果相同,缺失机制就是MCAR;如果各组均向量不全相同,那么提示缺失机制并非MCAR。
当数据集有J种缺失模式时,假设第j(j=1,2,…,J)个缺失模式组的观测指标服从均向量为μj且协方差矩阵为∑j的多元正态分布。检验各组的均向量是否相同就是检验假设:
H0:μ1=μ2=…=μJ,H1:μ1,μ2,…,μJ不全相等。


Chen和Little的文献指出,将广义估计方程应用于含缺失的重复测量数据的参数推断时,需要考虑是否服从MCAR机制[3],针对该情形,在Little的似然比检验基础上,又提出了基于信息分解和重组的Wald统计量检验,但该检验结果只适用于应用广义估计方程的情形,数理运算也较为繁琐复杂。同样针对应用广义估计方程的情形,Qu提出的广义得分检验(generalised score-type test)避免了繁琐数理运算过程[6],但依然只适用于该情形。
基于广义最小二乘法的检验:为了解决样本含量少无法满足似然比检验前提的问题,Kim和Bentler[7]提出了联合均向量和协方差阵的基于广义最小二乘法的检验方法。与Little的似然比检验类似,该方法仍然是将观测对象按照变量的缺失情况分组。不同之处在于,该检验不仅考察各组均向量是否相同,还进一步检验各组的协方差齐性。因此,统计量是均向量齐性统计量和协方差齐性统计量的组合,模拟研究显示,该检验犯Ⅰ型错误的风险小于Little的似然比统计法。
Park分类变量检验:针对重复测量数据中的分类变量,Park基于加权最小二乘法,提出统计量为Wald统计量的检验[8]。该方法将数据按照缺失模式分组后对每组拟合模型,检验模型参数的同质性,该方法的SAS程序包为CATMOD。由于该方法需要较大样本量保证近似正态性,Park又提出了基于广义估计方程的检验[9],在原有模型基础上,新模型在自变量部分加入表示对象是否在某一缺失模式组的指示变量,而并非分组建模,进而检验这些指示变量的回归系数是否都为0,如果回归系数不都为0且具有统计学意义,那么缺失机制不为MCAR。该方法操作较为简单,对连续或离散变量均可适用,较前面方法对样本含量要求更低。
改进后的Hawkins参数检验法:Hawkins检验是推断多变量成组设计资料方差齐性的方法[10]。Jamshidian和Jalal将该方法经改进后用于多变量缺失数据的MCAR机制识别。首先,已知总体为正态分布的情况下,运用极大似然法估计总体均向量和协方差阵。其次,基于均向量和协方差阵的估计值,在各个缺失模式组内根据似然函数计算缺失数据的条件分布函数,并使用单一填补法(single imputation)或多重填补法(multiple imputation)处理缺失数据,得到填补后的完整数据集;最后,采用Hawkins检验法判断填补后的各个缺失模式组的协方差阵是否相等,并以此得出是否拒绝缺失机制为MCAR的结论。
(2)非参数检验
上述参数检验方法均依赖于数据服从或近似服从正态分布,因而难以有效地识别非正态分布情况下的数据缺失机制。这种情况下需使用非参数检验验方法。
在Hawkins检验法的基础上,Jamshidian和Jalal又提出了基于Hawkins检验和Anderson-Darling检验的非参数联合检验法[12]。该方法不需要数据服从任何分布,只要求满足观测对象间的独立性及累积分布函数的连续性。非参数联合检验法的基本步骤与改进后的Hawkins参数检验法类似。二者区别在于:①不依赖总体分布的情况下,似然函数和缺失数据的条件概率分布都未知,因此该检验采用最小二乘法估计均向量和协方差阵,并使用回归填补法处理缺失数据;②针对填补后的完整数据集,考虑分布未知情况下的检验效能和运算效率问题,采用Anderson-Darlingk-样本检验法比较各组的协方差阵是否相等。
Li等指出Jamshidian提出的方法的核心是检验协方差齐性[11],所以对于非协方差的参数如峰度、斜度的同质性的检验能力较弱,因此提出一类更具有广泛应用价值的非参数检验方法。该检验方法能够取得较为满意的结果,但对数理要求较高,确定检验水准方法复杂。
(3)参数检验和非参数检验的联合使用
综合参数检验法和非参数检验法各自的优点,Jamshidian提出了一套针对MCAR机制的检验步骤(图3)[12]。其基本思路为:当数据来自一个正态分布总体,拒绝Hawkins检验意味着拒绝原假设即非协方差齐性;但如果数据总体分布未知,那么拒绝原假设还可能是因为服从的分布并非正态,因此在Hawkins检验为拒绝的条件下,应用一个非参数检验,如果拒绝该检验零假设,认为拒绝Hawkins检验原因并非数据不服从正态分布,机制不为MCAR;如果没有拒绝零假设,认为Hawkins检验未通过的原因是数据的总体分布并不服从正态分布。R包MissMech提供了该方法的具体实现。
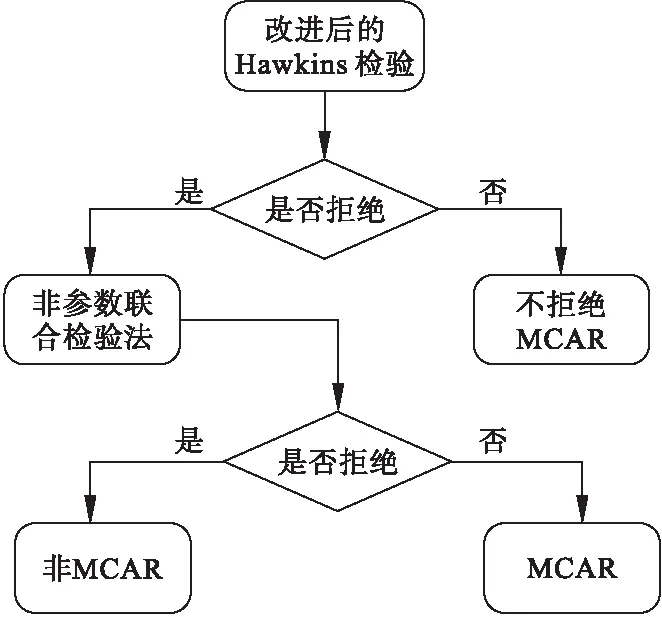
图3 Jamshidian非参数MCAR检验步骤
2.多变量重复测量数据的MAR机制识别方法
目前多变量数据的MAR机制识别方法研究主要针对重复测量数据。该类检验方法的总体思想是:按照已知影响缺失概率的因素对所有观测对象进行分组,如果数据的缺失机制是MAR,那么根据其定义可知,此时每个组内的缺失机制应为完全随机缺失。那么检验思路就为检验后一个时间点测量值是否与前一个时间点测量值来自同一总体。根据数据分布不同可分为参数检验和非参数检验。
(1)参数检验
Diggle提出的MAR机制识别方法旨在判定数据缺失在各自组内(若干实验组和对照组)是否是随机发生的[13],基本思想为:第二次随访开始分别在每个时间点各组内寻找是否有研究对象的观测值发生缺失;如果有,回溯到前一个时间点上通过假设检验的方法判断这些研究对象的观测值是否是该组内所有观测对象观测值的随机样本,并记录下每次假设检验的P值。Diggle认为,在MAR机制的假设下,这些P值应服从[0,1]的均匀分布。因此Diggle采用Kolmogorov统计量衡量P值与[0,1]均匀分布的差异程度,判断缺失机制是否为MAR。
Ridout[14]指出缺失模式为单调缺失模式(monotonous missing pattern)的情况下,即在某一时间点数据缺失后后续时间点均缺失,可以利用logit回归模型来判定缺失机制是否为MAR,即缺失的产生是否与协变量相关。按照情况的复杂与否,可以将建模分为条件logit回归模型和非条件logit回归模型。但该方法建模十分复杂,它基于的假设每个时间点的数据是独立的往往不成立。与Ridout的方法类似,Fairclough的机制检验方法也是利用logit回归模型[15],不同的是它不要求单调缺失模式,因此适用性更加广泛。
Diggle的方法比较直观,但Listing指出Kolmogorov统计量同Ridout的统计量一样依赖于每次测量的独立性[16],显然这个假设常不符合重复测量情况。另外,当P值的个数太小时,Kolmogorov检验的效能很低。因此,他提出了一种基于均值比较的检验方法。该方法与Diggle的方法类似的是,同样是从第二次随访开始的每个时间点t(t>2)上寻找发生变量缺失的研究对象。二者的区别在于,Listing方法是回溯到前一个时间点(t-1)上,通过将这些研究对象的平均观测值与完成整个随访的研究对象的平均观测值相比较,得出(t-1)时间点上的均值之差,最终以各个时间点上发生缺失的样本数作为权重,构建加权意义下的均值之差作为检验统计量。模拟研究发现Listing方法在大样本情况下表现稳定,比Diggle方法具有更强的检验效能。
(2)非参数检验
针对前一种参数检验不适用于非正态分布数据的情形,Listing又提出了一种非参数检验方法[17],该方法基于队列中发生缺失的对象观测值应大于(或小于)未发生缺失的对象的相应观测值的假定。首先在每一个时间点上分别进行Wilcoxon秩和检验,比较在该时间点上缺失和未缺失对象观测值的累积分布函数是否存在差异。在随机变量Yit是连续型的情况下,不同时间点Wilcoxon统计量是独立的,因此可将它们合并后得到联合检验统计量S。根据中心极限定理,S渐近服从标准正态分布,最终根据基于S的假设检验结果做出推断。同样针对Listing提出的参数检验法,Norbert提出了基于重抽样(bootstrap)的非参数方法[18],统计量是加权组合每一次测量时缺失组和非缺失组之间的差别后的非参数统计量,原理类似于Listing提出的非参数方法,只是使用了重抽样技术。模拟实验发现,该方法对于偏态分布可取得良好的效果。
Deny提出了一类非参数的采用logit回归的方法[19],即用参数化的方法处理,用一组正交积来表示,从而将MAR机制的检验转化为检验参数是否具有统计学意义的过程。若参数具有统计学意义则机制为MAR,但该方法较为复杂。
3.多变量重复测量数据的MNAR机制的识别方法
此外,孙捷等认为在某些情况下,确认机制并非MCAR后,非单调缺失模式的重复测量数据是MNAR的一种典型形式[20],比如对医院病人的生命质量进行纵向随访时,如果因为病人搬家而导致数据某时点后的缺失,则认为缺失与前期观察(地址)相关,机制可能为MAR,具体是否为MAR需作进一步检验;但某一时点后数据又再次出现,那么数据缺失不与前期观察相关,机制为MNAR,该方法简单易行,但需结合实际情况分析。
讨 论
数据缺失广泛存在于医学研究中,对研究结果的准确性造成很大的影响。在观察性研究和实验性研究中,针对信息缺失往往采取一系列措施进行预防,或者尽可能对缺失信息补回。通过数理方法对缺失数据进行填补的方法并未引起足够的重视,虽然这个方法是经济且可行的。
国内外针对数据缺失的填补方法较为系统,但是针对填补方法对应的数据缺失机制识别的相关研究,国外较为成熟,主要针对数理方法进行阐述,但并不系统;国内研究较少,局限于单变量数据,且缺少对其适用数据类型的说明。本文系统地总结了国外各类成熟的对多变量数据缺失机制的识别方法,并指出了适用的数据类型,具有一定的借鉴意义。但数据缺失尤其是多变量数据缺失的机制在实际情况中是十分复杂的,所以需要考虑具体的研究内容,结合多种方法对数据缺失的机制进行判定。
[1] Rubin,Donald B.Inference and Missing Data.Biometrika,1976,63(1):581-92.
[2] Fielding S,Fayers PM,Mcdonald A,et al.Simple imputation methods were inadequate for missing not at random(MNAR)quality of life data.Health and Quality of Life Outcomes,2008,6:57.
[3] Chen HY,Little R.A test of missing completely at random for generalised estimating equations with missing data.Biometrika,1999,86(1):1198-1202.
[4] Dixon WJ.Bmdp statistical software.Biometrics,1982,38(2).
[5] Little RJA.A Test of Missing Completely at Random for Multivariate Data with Missing Values.Journal of the American Statistical Association,1988,83(404):1198-1202.
[6] Qu A,Song XK.Testing ignorable missingness in estimating equation approaches for longitudinal data.Biometrika,2002,89(4):841-850.
[7] Kim KH,Bentler PM.Tests of homogeneity of means and covariance matrices for multivariate incomplete data.Psychometrika,2002,67(4):609-623.
[8] Park T,Davis CS.A test of the missing data mechanism for repeated categorical data.Biometrics,1993,49(2):631-8.
[9] Park T,Lee SY.A test of missing completely at random for longitudinal data with missing observations.Statistics in Medicine,1997,16(16):1859-1871.
[10]Hawkins DM.A New Test for Multivariate Normality and Homoscedasticity.Technometrics,1981,23(1):105-110.
[11]Li J,Yu Y.A Nonparametric Test of Missing Completely at Random for Incomplete Multivariate Data.Psychometrika,2015,80(3):707-726.
[12]Jamshidian M,Jalal S.Tests of homoscedasticity,normality,and missing completely at random for incomplete multivariate data.Psychometrika,2010,75(4):649-674.
[13]Diggle PJ.Testing for Random Dropouts in Repeated Measurement Data.Biometrics,1989,45(4):1255-1258.
[14]Ridout MS.Testing for random dropouts in repeated measurement data.Biometrics,1991,47(4):1619-1621.
[15]Fairclough DL.Design and analysis of quality of life studies in clinical trials.Quality of Life Research,2002,13(1):275-277.
[16]Listing J,Schlittgen R.Tests If Dropouts Are Missed at Random.Biometrical Journal,1998,40(8):929-935.
[17]Listing J,Schlittgen R.A Nonparametric Test for Random Dropouts.Biometrical Journal,2003,45(1):113-127.
[18]Schmitz N,Franz M.A Bootstrap Method To Test If Study Dropouts Are Missing Randomly.Quality & Quantity,2002,36(36):1-16.
[19]Pommeret D.Testing the mechanism of missing data.
[20]孙婕,金勇进,戴明锋.关于数据缺失机制的检验方法探讨.数学的实践与认识,2013,12:166-173.
国家自然科学基金青年基金(No.81602935);四川大学青年教师科研启动基金(2016SCU11006);四川省卫生信息学会公共卫生信息专业委员会
△通信作者:张韬, E-mail:scdxzhangtao@163.com;李晓松,E-mail:lixiaosong1101@126.com.
张 悦)
