住院医疗费用分布拟合研究*

霍振昂 王仲阳 孙 韬△

住院医疗费用分布拟合研究*

霍振昂1王仲阳2孙 韬1△

住院医疗费用分布的特点一般为左偏、厚尾，尾部趋于零的速度缓慢，国内外研究者一般采用重尾分布族模型对其密度函数和分布函数进行刻画。本研究拟从大样本角度对住院医疗费用分布模型进行拟合。

数 据

本研究数据来源于2015年河南省国家卫生统计直报系统病例首页(卫计统表 4-1，字段名:ZYF)报表，删除了缺失值、零值等无效信息值，对住院费用小于 100 的病例也做了删除处理。清洗后的数据共5023135 例，涵盖了 253 家医院上报数据。

表1显示一级医院数据量非常小，仅有 14267 例，占比2.8%，绝大部分病例来自二级以上医院；医院级别与住院医疗费用均值、中位数均存在明显的正相关，检验结果证实了这一点( Kruskal-Wallisχ2=978650,P<0.01)。

表1 河南省医院住院费用基本情况表

模 型

综合仇春涓[1]、薛秦香[2]等人的研究，本文利用重尾分布族模型(对数正态、 Pareto、 Weibull、 Burr和loglogis 分布)分别进行了拟合。设x为随机变量，且x>0,各分布模型的概率密度函数和分布函数，分别如下。

1.对数正态分布

2.Pareto 分布

3.WeiBull 分布

4.Burr分布(Type XII)

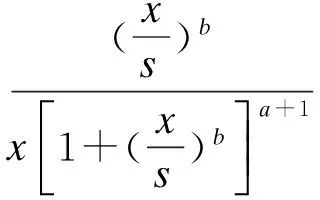
5.loglogistic分布

结 果

应用R软件对住院医疗费用数据进行拟合，得到拟合参数，并绘制相应直方图和概率密度图。

图1、图2和图3分别显示了对数正态、Pareto和Weibull分布的拟合情况。从图中可以直观地看出，三个模型参数都在 1%水平上显著，但数据拟合情况均不太理想，与直方图显示的实际概率密度相比，均有较大的偏差，上述 3 个模型均未能很好地刻画出住院医疗费用分布的变化趋势。

图4、图5分别显示了Burr分布和Llogistic分布拟合情况。如图中显示，两个分布概率密度函数从始至终反映出了直方图的变动趋势，契合度非常高。如前所述，当Burr概率密度函数参数a=1时，实质上就转化了Llogistic分布，这一点从图5中可以看到， Llogistic分布估计参数与Burr分布后两个估计参数完全一致，并且Llogistic参数的标准误更小,表明在相同条件下，其参数估计的精度相对更高，更加有效。综合图1～5情况初步分析，相对于其他模型，采用Llogistic分布模型得到概率密度图与直方图拟合效果最好。

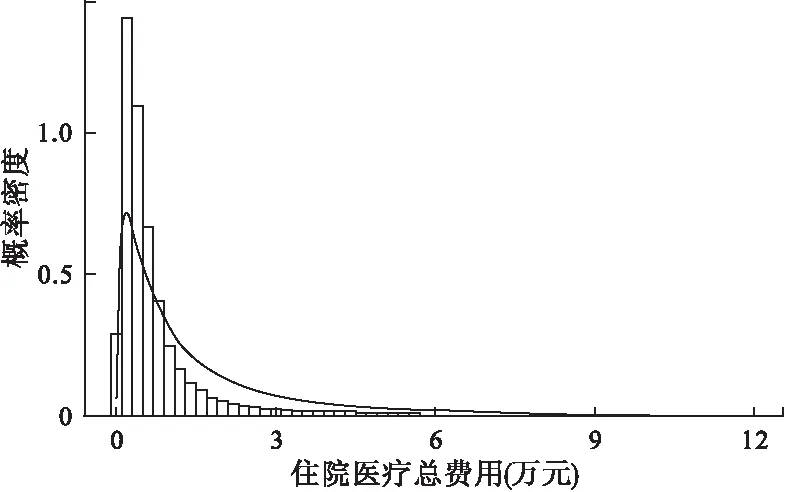
图1 对数正态分布模型拟合图

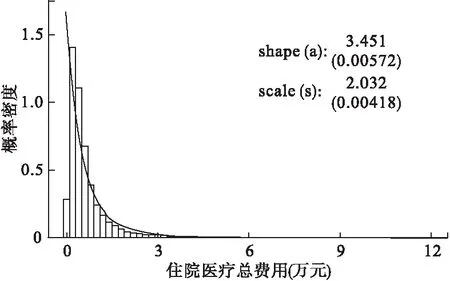
图2 Pareto分布模型拟合图

图3 Weibull分布模型拟合图

图4 Burr(Type XⅡ)模型拟合图

图5 Llogistic分布模型拟合图

从表2反映的各分布模型累积概率对比情况看,Burr、Llogistic模型也要大大好于前三个模型，在所划分的离散区间上，前两个模型与实际累积概率都非常接近，尤其是在对两端数据累积概率拟合时，几乎与实际概率分布值相等。相比之下，其余三个模型的拟合度要差很多，尤其是对数正态分布模型拟合出的效果，偏离实际值甚远。

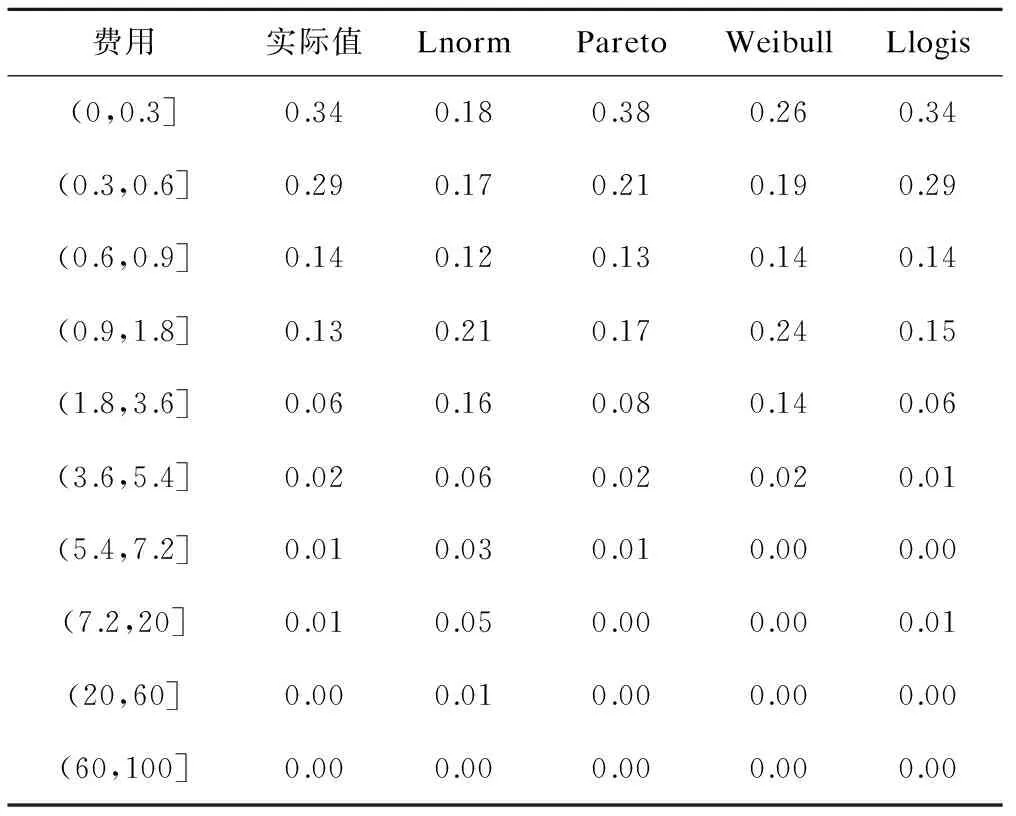
表2 各分布模型累积概率对比情况

图6汇总显示了各分布模型的累计密度图，从中可以清晰地看出，Llogistic和Burr模型累积概率曲线几乎与实际累积概率曲线重叠，而其余三个模型的累积概率曲线图则相对偏离较远。综合累积概率密度拟合情况判断，住院医疗费用依然最有可能符合Burr和Llogistic分布。

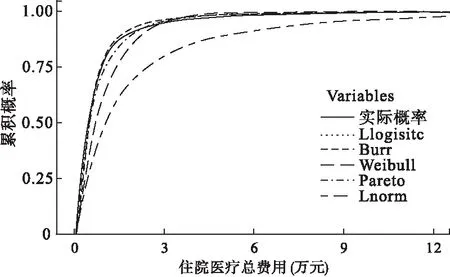
图6 各分布模型累积概率汇总

由于样本量过于庞大，难以找到直接的方法对模型进行分布拟合检验，本研究采取了 Bootstrap 方法进行替代。

表3 Bootstrap检验结果汇总表

整个检验步骤在R软件中通过编程实现，具体步骤如下：第一步，建立H0:总体符合(某种)模型分布，H1:总体不符合该模型分布类型，置信水平α=0.01；第二步，对住院医疗费用进行有放回随机抽样，每次抽取2000个样本；第三步，根据不同分布模型概率密度函数公式计算并记录样本参数拟合值，进行K-S检验(置信水准设定为5%，如果K-S检验报告的P值>0.05，则认为通过，否则为不通过)，记录相应结果；第四步，重复上述第二步、第三步N次；分别计算N个参数拟合值的样本方差，做为参数拟合值的方差估计量。第五步，以K-S检验通过次数与总抽样次数(N)之比为统计量，计算相应P值，作出统计推断。

检验结果列在表3中Burr和Llogistic模型通过K-S检验的次数分别为996次、 997次(N=1000)和4979次、 4983次(N=5000),相应的P值分别为0.996、0.997。其余三个模型则没有通过K-S检验的记录，相应的P值均为0。检验结果表明，在1%的置信水准下，不能拒绝总体符合Burr分布和Llogistic分布的原假设；可以拒绝总体符合Lnorm分布、Pareto分布和Weibull分布的原假设。通过表3还可以看出，抽样1000次与5000次的结果整体差别不算太大。通过抽样计算参数均值几乎与医疗费用总体均值相等，但标准误更加稳健。

讨 论

判断数据分布类型对于统计和计量建模的重要性不言而喻。如果分布类型假定错误，在进行相应参数估计时则很可能得出有偏估计值。如在以往一些对医疗费用的研究中，直接将医疗费用做对数转换，仅从图形上判断就做出数据符合对数正态分布，进而采取相应的方法进行参数估计。从本研究结果看，并未找到住院费用符合对数正态分的证据，因此不加判断直接采取这样的做法一定要慎重。

此外需要注意的是，住院医疗费用厚尾的特征非常突出，在本研究所收集到的数据中， 95分位以后的样本费用合计数占到了总数的34.5%。在这样的情况下，如果采取以往的算数平均来计算次均住院费用的话，实际上并不能很好地反映住院医疗费用的集中趋势。这也提示我们，判断次均医疗费用的高低，不能仅凭均值来进行，还需要研究更有效的评判指标。

[1] 仇春涓,陈滔,吴贤毅.重尾分布下医疗保险保费合理性评估——基于上海市闵行区新农合的实证研究.数理统计与管理,2013,6:974-983.

[2] 薛秦香,胡安霞,陈璐.新型农村合作医疗住院费用损失分布拟合.中国卫生经济,2012,6:35-36.

[3] 沈颖,尹娟,傅陈欣熹.南昌市某三甲医院住院费用结构研究.中国卫生统计,2016,(3):491-492.

[4] 许建强,郑娟,井淇,等.山东省某市新农合大病保险补偿 20 类大病费用分布情况及效果评价.中国卫生统计,2016,(1):81-84.

[5] Marazzi A,Yohai V.Adaptively truncated maximum likelihood regression with asymmetric errors.Journal of Statistical Planning and Inference,2004,122:271-291.

[6] Gilleskie DB,Mroz TA.A flexible approach for estimating the effect of covariates on health expenditures.Journal of Health Economics,2004,23:391-418.

[7] 王新宇,宋学锋.拟合中国股票市场收益的统计分布.系统工程理论与实践,2006,12:40-46.

河南省重点科技攻关项目(1042102310142)

1.河南医学高等专科学校 (450000) 2.河南省卫生计生委

△通信作者：孙韬，E-mail:549130@qq.com

刘 壮)