利用多样化算法，培养学生数学核心素养

邢艳++范文贵

【摘 要】原创一道网格背景下多种算法解决多边形面积的题目，可以有助于培养学生的数学核心素养。具体而言，可以通过以下路径展开：研发学习素材，为学生创设研究问题的空间；鼓励独立思考，培养科学精神；在个性化解法的生成中，培养学生勇于探索的精神；在算法多样化的交流中培养学生理性思维；在活动经验的积累中，培养学生批判质疑的精神。特别是当学生遇到看似无法解决的问题时，鼓励学生探索问题解决的新途径，培养学生反思问题的解决过程，从而更好地感悟学习方法。

【关键词】网格多边形；数学核心素养；问题解决；理性思维

数学核心素养是以培养能够适应现代社会生活的公民为目标，以教育各阶段相应的数学核心知识为载体，培养学生数学创新能力，激发学生主动思考的意识，形成积极的数学态度，并为学生的可持续发展提供强有力的支撑。在小学数学课堂教学中落实数学核心素养应注重培养小学生理性思维、批判质疑、勇于探索的科学精神，以及在反思中学会学习，在问题解决中实践创新。

一、研发学习素材，创设研究问题的空间

好的学习材料能唤醒学生原有的数学活动经验，并能主动运用经验去解决新的问题，从而触发其积极思维、主动参与，并在思考与解决问题的过程中形成多元的、独特的问题解决方案，使后续的交流碰撞、实现经验的优化与提升成为可能。我们原创了一道网格背景下多种算法解决多边形面积的题目。

图1中每个方格的面积为1cm2，请同学们用多种方法求这个多边形的面积。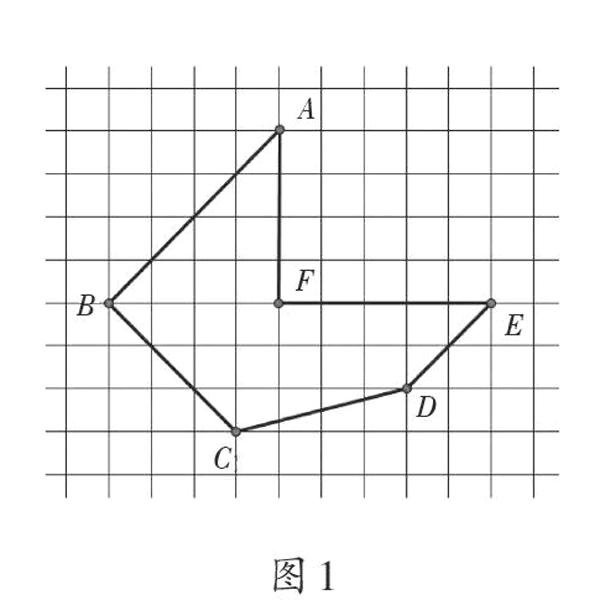

该原创题为解决问题方法的多样性提供了可能，同时在学生将组合图形割补为基本图形的过程中，所学过的基本图形都将一一呈现，使得教学过程更为系统、完整。

二、鼓励独立思考，培育科学精神

科学精神主要是学生在学习、理解、运用科学知识和技能等方面所形成的价值标准、思维方式和行为表现。具体包括理性思维、批判质疑、勇于探究等基本要点。

（一）在个性化解法的生成中培养勇于探索的精神

在算法多样化的教学中，教师应尊重学生的个性特征，给予学生独立思考的机会，激励学生自主探索，允许不同的学生从不同的角度认识问题，以不同的方式表达问题，用不同的方法探索问题，使学生个体尽可能找到自己的算法。

在独立思考的过程中，有的学生在方格纸上分割出第一种方法（如图2），计算时却发现“三角形FCD的底和高是多少”不能确定，求不出三角形的面积。他立即改变思考的角度，方格纸上又呈现出第二种、第三种、第四种方法，他又发现这三种方法中也都出现了类似于第一种方法的问题，即在分割的图形中总有一个三角形的底和高不能确定，求不出三角形的面积。在一次又一次地探索中，终于，他寻求到了能计算出这个多边形面积的方法。

也有的学生认为自己的方法虽然能计算出多边形的面积，但比较烦琐，通过不断地改变辅助线，最终简化了分割方法。

还有的学生除用分割法转化图形外，又使用添补法转化图形。

核心素养是一个融知识、技能、态度和价值观于一体的集成系统，在价值观的推动下，学生对数学问题产生好奇心和想象力；他们不畏困难，坚持不懈地探索；在运用知识与技能的过程中，大胆尝试，积极寻求有效解决问题的方法。这样学生才能形成相应的数学素养。

（二）在算法多样化的交流中培养理性思维

学生提出各种个性化的算法后，教师组织学生互动交流，以归纳整理出“多样化”的算法。学生不仅能认识从不同角度得出算法，而且能更好地展开交流和討论，期间进行纠正、补充和完善，共同分析探究过程，评价探究结果，分享探究成果。

在互动交流的过程中，教师与学生一起将多样的方法按转化的角度不同分成三类。

第一类，从图形内部寻找解决问题的路径。

（1）以“BF”“MD”为主线的分割方法（如图3）。

（2）以“BF”“OC”为主线的分割方法（如图4）。

（3）以“QM”“MD”为主线的分割方法（如图5）。

（4）以“QC”为主线的分割方法（如图6）。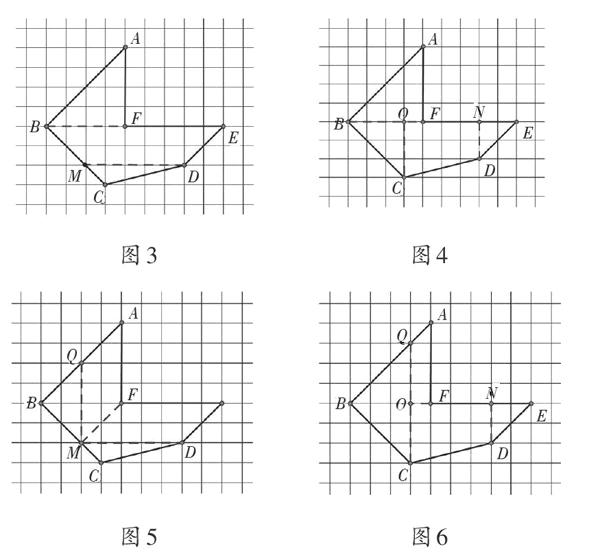

学生的关注点聚焦于图形的内部，用分割的方法将多边形转化为几个基本图形后再计算面积。由于观察图形的角度不同，分割图形的切入点也不相同；加之学生对各种基本图形的熟悉程度存在差异，进一步分割出的图形亦有所不同，分割的结果有繁有简。因此，以上这四种方法各自还包含了不同的变形。

第二类，从图形外部寻找解决问题的路径。

其思路是从整体观察多边形，在其外部添补一个长方形（如图7）。多种变形的不同之处集中于四边形CDEG的分割，除图7的方法外，还可以过D点作CG的平行线交EG于M，也可以直接连接DG。

第三类，内外综合寻找解决问题的路径。

将整个图形分割为两部分思考，上面是三角形ABF，可直接计算其面积；下面的四边形BCDE用添补法进一步转化后再计算面积。该方法的不同之处体现在四边形BCDE的转化思路上，有三种形成。

（1）将四边形BCDE添补为矩形BJGE（如图8）。

（2）将四边形BCDE添补为直角梯形BCGE（如图9）。endprint

（3）将四边形BCDE添补为等腰梯形BCLE（如图10）。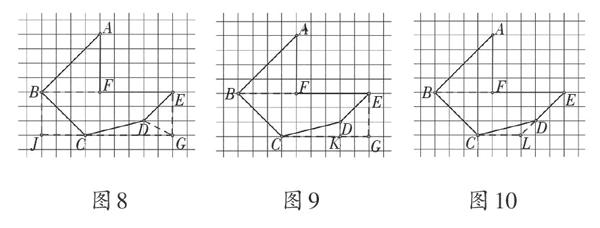

通过观察、比较、分类，学生发现这些转化方法之间的联系与区别，并抽象、概括出每种思路的一般特点，将零散的、个别的转化方法系统化和条理化，形成多维度的观察视角。同时深刻地认识到转化方法在解决问题中的作用，是基于对图形的构成（质）与图形的组成形式（现象）的认识，这是一个隐含了哲学思辨（现象与本质的关系）的辩证唯物主义过程。在这个过程中，学生要认识分解与组合、恒等变形，也要认识处理现象与本质的基本方法，从而感悟数学推理思想。

（三）在活动经验的积累中培育批判质疑的精神

在学生的转化方案中出现最多的是图2。他们也都认为这是“无法解答”的方法，因为无法确定三角形FCD的底和高是多少。这种方法被大家一致判断为不可行的同时，学生中发出了“有办法解答”的声音。学生原本平静的脑海，又掀起了思维的波澜，惊讶之后又凝神沉思。

“难道你能找到三角形的底和高吗？”

“能不能把三角形FCD转化成我们知道的图形并计算它的面积呢？”一石激起千层浪，在座的学生豁然开朗。

这个提出质疑的学生，将转化思想建构到自己的认知结构中，进而迁移到解决三角形FCD的面积计算上来，才提出突破思维定势的问题。这就是数学思想的力量，既能解决问题，又是下一个问题的孵化器。通过独立思考，学生获得了属于自己的经验；长期活动经验的积累，又使学生获得了思维方法，最终达到的目标就是学会思考。创新依赖的是思考，是数学活动中创造性的思维。因此，独立思考、学会思考是创新的核心。

三、反转不可行，探索问题解决的新途径

学生在学习过程中获取前人和他人从没有获取的新知识、新技术、新能力或对前人和他人已获取的知识有新的思路、新的理解、新的解释和新的应用就是创新。来自学生的提问把所有学生带入激活已知、产生心向、激发创造的问题情境。

通过合作探究，学生创造出了四种不同的方法。

1.将三角形FCD添补为矩形OCKN（如图11）。

2.将三角形FCD添补为直角梯形FCKN（如图12）。

3.将三角形FCD添补为三角形FXY（如图13）。

4.将三角形FCD在内部分割为三个三角形（如图14）。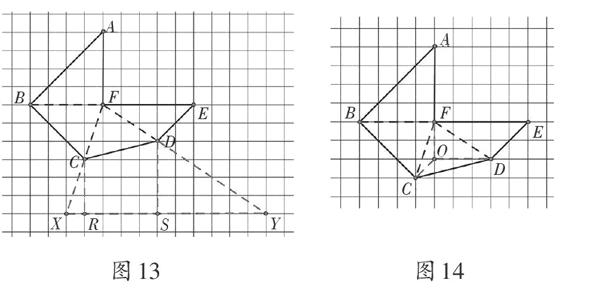

通过以上方法的转化都可以计算出三角形FCD的面积，因此图2的方法得解，将不可行变为可行！这四种方法对学生而言是前所未有的，彼此之间又是与众不同的，每种方法都是个人思维水平的突破。从思路上，这四种方法反映为不同的创新技法，图11和图12属于类比借鉴法，其思路来源于图8和图9的转化方法。图13属于拓展解题思路，在延长三角形两边的过程中寻找与网格线重合且端点能落在小正方形顶点上的第三边。其目的是使放大的三角形中有一条边与网格线重合，就可以知道大三角形的一组底和高，进而用添补法计算面积。图14属于缩小思路，切入点是三角形FCD中的直角三角形FOD，它的两条直角边与网格线重合，这是有利的转化条件。然而，这四种转化方法的目标都聚焦在利用与网格线重合的边构造新图形上，比之前的转化过程凸显解决问题的本质，让我们清晰地感受到学生思维的深入和品质提升的过程。

凭借经验和直觉，学生认为“不知道三角形的底和高是多少，就不能计算三角形的面积”这个结论是错误的，是学生普遍存在的真问题。学生的大胆质疑推进课堂教学的进程和思维的深入。通过对新问题的探究，其成果令人振奋，学生不仅纠正了原先的错误想法，认识到底乘高再除以2是求三角形面积的一般方法，但不是唯一的方法！在挑战中，学生清晰地感受到自己学习的功夫仿佛又精进了一步。原来，挑战和學习被学生感知，是数学学习的必要要素，在问题解决中实践创新的核心素养得到了培养。

四、反思问题解决过程，感悟学习方法

反思是对自己的思维过程、思维结果进行再认识的检验过程，它是学习中不可缺少的重要环节。我们可以以三个问题引导学生反思。

（一）学习是思考的基础，思考是学习的灵魂

“这节课我们做了哪些事？”这节课学生先通过独立思考，自主探索解决问题的方法；然后进行比较归纳，梳理出多维度解决问题的路径；最后通过对不可行解法的挑战，实现了问题解决的新突破。学生的思维一刻不曾停歇。他们在思考中摸索，在思考中优化，在思考中质疑，在思考中创新，使分析综合、比较鉴别、抽象和想象等思维能力得到全面的、均衡的发展，完整地经历了问题解决的全过程。

（二）获得学习方法，是一切学习之母

“你对哪个环节印象最深？”学生一致认为“不能把三角形FCD转化成我们知道的图形计算它的面积吗？”这个问题的提出和图11至图14的解法令他们印象深刻。从图2的不可行到可行解法的探索是学生对转化方法深刻理解和熟练掌握的具体表征。学习中的创新就是敢于用怀疑的眼光去审视既成的事实，对已获取的知识有新的思路、新的理解、新的解释和新的应用。

（三）积极的态度是学习中最有价值的财富

“你对自己最满意的表现是什么？”“我能想出好几种方法！”“我的方法最简捷！”“我把图2的方法变成可行的了！”……学生的畅所欲言呈现出积极的学习态度和勇于探索的精神。他们想学、肯学、 勤学、会学，这些可贵的学习品质是学会学习的前提。

小学生数学核心素养的培养是一个潜移默化、日积月累、不断发展和提高的过程。教师应该把对小学生数学核心素养的培养落实到每一节数学课中，寓于具体数学知识技能的教学之中。既注重“有形”的数学概念、法则、性质、定律、规律等显性知识的教学，又要注重引导学生深入体悟隐藏在这些知识背后“无形”的、体现数学知识本质的数学思想方法、核心素养。

（天津市南开区教育中心 300110

天津师范大学初等教育学院 300110）endprint