例谈小学数学学科内课程整合的实施策略

姚荣金

【摘 要】小学数学学科内课程整合实施是指小学数学课程内的教学目标、教学内容、教学方法的整合，也即指课程实施過程中内容与资源的整合。具体而言，小学数学学科内整合可以划分为以下几类：1.重组式课程整合，主要应用于教学内容的整合；2. 相关式课程整合，主要是对运用相同数学思想方法、前后相关联的课时进行整合；3. 根源式课程整合，主要是根据学生学习基础，以及知识间的联系对复习课进行相关整合。课程整合其实是一个梳理的过程，在具体实施过程中，教师可以采取对应策略有效展开，让学生联系着学知识，自主建构个体独特的知识网络。

【关键词】小学数学；课程整合；实施策略

整合就是通过协调、融合，将零散的要素组合在一起。《浙江省教育厅办公室关于促进义务教育课程整合的指导意见》（浙教办基〔2015〕79号 ）文件指出：课程整合实施是指课程内和课程间的教学目标、教学内容、教学方法的整合，也指课程实施过程中课内外的整合……学校应根据教学实际，从学科内的局部整合到学科间的主题整合，再到“全课程”的统整，逐步推进。由此可见，小学数学学科内课程整合实施是指小学数学课程内的教学目标、教学内容、教学方法的整合，也即指课程实施过程中内容与资源的整合。在深化课改的进程中笔者发现课程整合实施是当前学校深化课程改革的主要途径之一，学科内课程整合实施是学科教师努力实践的基础。围绕立德树人目标，针对学生身心发展特点，依据国家课程标准与学生核心素养要求，笔者对小学数学相关课程内容进行整合实施，以期增强课程实施的综合性和实效性。

一、重组式课程整合实施策略

重组式课程整合主要应用于教学内容的整合。举个例子，六年级是小学学习阶段的最后一年，学生所学的数学知识比以往更综合、更复杂、知识间联系更密切。根据学生已有认知基础和数学知识间的联系，笔者对六年级数学教材进行梳理，科学、合理地调整课时内容，进行重组式课程整合实施。以六上第一单元“圆”为例，通过对知识点的整理我们把这一单元中的内容作了4个调整，具体如下。

第一个调整：“圆的认识（一）”第一课时的目标是在画圆的过程中，理解同圆中半径、直径以及直径和半径之间的关系，体会圆心和半径之间的关系；“圆的认识（二）”的目标是探索并发现圆是轴对称图形、有无数条对称轴，体会圆的对称性。两课时都是在学习圆的特征，而且圆的对称轴刚好和直径有必然的联系，这两课时整合成了一课时，学生学习更有效。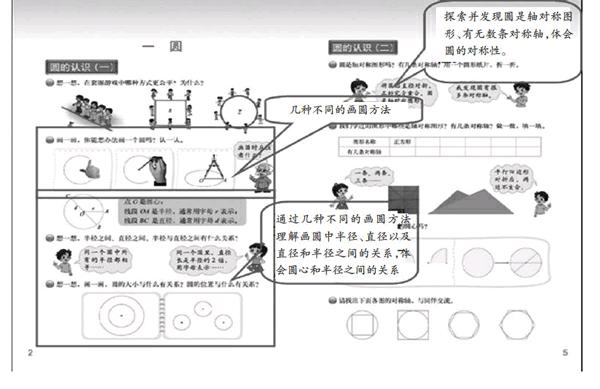

第二个调整：“圆的认识（一）”第二课时和欣赏与设计整合成一课时。有利于学生理解圆的特征与生活的联系，提高学生根据圆的性质进行问题解决的能力。

第三个调整：圆周率的数学文化知识与圆的周长学习整合为一课时。当讨论圆的周长和直径间有什么关系的时候，可以出示圆周率历史中的三种方法，以阅读的形式让学生了解有哪些方法可以知道周长和直径间的关系，然后由学生选择一种好操作的方法进行验证，最后出示圆周率的历史这一课中有关的一些数据。数学文化与知识有机整合才具有生命活力，才是学生进一步学习数学的原动力。

第四个调整：“圆的面积（一）”第一课时主要是结合实例认识圆的面积，并经历圆面积计算公式的推导过程。除了把圆转化成平行四边形外还有很多其他的方法，可以把“圆的面积（二）”中的例三将圆形的垫片剪开恰好是一个底为圆的周长、高为圆的半径的三角形以及练一练第三题将圆形的垫片剪开得到两个近似的三角形，再拼成一个底为圆的周长的一半、高为圆的半径的平行四边形整合在一起，有利于学生体会通过转化成不同的图形都可以推导出圆的面积等于πr2。

二、相关式课程整合实施策略

对运用相同数学思想方法、前后相关联的课时进行相关式课程整合实施，有利于学生综合有效地掌握知识，更能触类旁通，举一反三。

例如，五年级上册第三单元的“找因数”和第三单元的“找质数”可以整合为一节40分钟的课。“找因数”这节课，学生要学会在1～100的自然数中，找到某个自然数的所有因数，“找质数”正是根据因数的个数把自然数（0除外），分成质数、合数和1，因而这两节课可以整合成一节课。在教学时，当学生掌握找一个数的所有因数方法后，出示15、21、3、4、5、7、9、45、1这样一组数，让学生根据因数的个数，把这些数分成两类，并追问：你们是怎么分类的？引出“质数”和“合数”的概念，并提出1既不是质数也不是合数。

例如，在上完第四单元的“平行四边形的面积”和“三角形的面积”这两节课的第一课时后，这两节课的“试一试”可以整合成一节40分钟的课。两节课的“试一试”运用的数学思想方法是一样的，第1题都是用公式的逆运用和列方程这两种方法解决问题的，第2题让学生通过计算明白“同底等高的平行四边形、三角形的面积是相等的”。而且学生在学习完平行四边形后，根据知识的迁移，能更好、更快地掌握三角形的知识。

例如，六上第二单元的“分数的混合运算（二）”的主要目标是结合具体情境，会画图表示“增加几分之几”或“减少几分之几”的意义及计算，而“百分数的应用（二）”的目标也是会画图表示“增加百分之几”或“减少百分之几”的意义及计算，在解决问题的策略上是一样的，正因为在分数中已经具体学习了用这样的策略解决这类题，那在百分数计算中就可以缩短时间，因此，笔者认为可以把“百分数的应用（二）”的2课时缩短为1课时。

又如，“分数混合运算（三）”和“百分数的应用（三）”也是这样，我们可以具体来看一看。都是通过画图、找等量关系、列方程解决此类问题，因此我们觉得同样可以把“百分数的应用（三）”的2课时整合成1课时。

在实践中，这样的教学既节省了时间，又有利于学生理解、掌握知识，学生学得有效、轻松，教师教得顺手、舒心。

三、根源式课程整合实施策略

关于复习课，笔者是根据学生学习基础，以及知识间的联系，进行根源式的整合实施的。例如，总复习，教材中是把复习整数和复习小数、分数、百分数分开来的。事实上，可以把这两部分整合在一起复习，因为不管整数、小数、分数还是百分数，其实这些数都具有同根源的共通点，教师可以从数的意义、组成、计数单位等方面复习，比如整数部分的个位上的数表示几个一，十位上的数表示几个十，百位上的数表示几个百，小数部分的十分位表示几个0.1，百分位表示几个0.01，而分数同样有自己的分数单位，理解了数的意义就可以比较数的大小，进一步梳理整数、小数的数位顺序表及相关知识，接着可以复习数的属性等，比如奇数、偶数、质数、合数、公因数、公倍数等。等梳理完这些知识点后，让孩子静下心来安安静静地完成后面相对应的作业，对于基础好的同学可以另外增加一些挑战题，最后针对错误率高的题目进行分析总结。

例如，图形与几何领域的复习，可以引导学生感悟“点、线、面、体”之间的关系。以点可以做端点，引出线段、射线；点可以做顶点，引出角；点还可以做起点；等等。让学生体会点运动成线、线运动成面、面运动成体，沟通各种图形之间的联系，最后建构“图形与几何”的知识网络。

小学数学课程整合其实是一个梳理的过程，把所有相关联的知识连成线，形成知识脉络，通过多阶、多维地梳理，让学生联系着学知识，自主建构个体独特的知识网络。

（浙江省浦江县教育研究与教师培训中心

322200）endprint