低年级学生对应思考中的直觉规律

郜舒竹

【摘 要】数学学习过程中经常需要对应思考的过程，学生在这样的思考过程中经常会出现各式各样的错误，错误的背后蕴含着符合学生年龄特征的直觉规律。主要反映为：数量相同、意义相同和顺序相同。发现这样的直觉规律有益于教师解释学生出现的错误，读懂学生数学学习过程中的思维。

【关键词】错误；直觉规律；对应思考

数学学习中经常需要对应思考，比如将“三百二十一”写为“321”的过程，就需要对数的汉语表达与数字表达两者之间进行对应思考。在计算中需要对参与运算的数之间进行对应思考。解决文字问题时需要对文字信息与算式或者图形之间进行对应思考。学生在进行此类对应思考过程中，经常会出现依据自身直觉产生的理解，其中一些理解具有普遍性和必然性，因而也就具有规律性。努力发现这样的直觉规律（Intuitive Rule），有益于教师解释学生产生错误的合理性，读懂学生思维的规律性。

一、语言转换中的直觉与误解

在思考与两个或者多个结构之间对应关系有关的问题时，人们潜意识中会对不同结构之间的对应关系有一种自己的直觉理解，而后的思考就会沿着这样的理解继续下去。比如，在思考将“我是一名教师”这句话翻译为英文的时候，潜意识中会把这句话看作是一个由“我”“是”“一名”和“教师”四个元素构成的结构，直觉理解是只需要将对应元素的英文单词与相应的汉字或者词汇一一对应地组合起来，做到“元素数量相同、元素顺序相同、元素意义相同”，就完成了翻译（见图1）。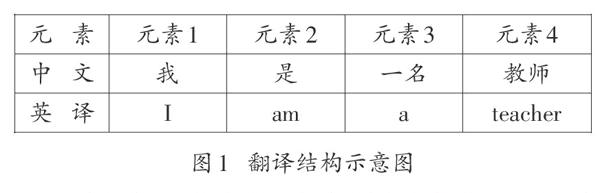

而事實上，这样的直觉理解在有些情况下是可以的，在许多情况下却是不适用的。比如将两人见面时常说的问候语“你好”翻译为英文，就不能采用一一对应的方式翻译为“You good”。“早上好”也不能翻译为“Morning good”，等等。因此这种“数量相同、顺序相同、意义相同”的直觉理解，实质上是结构之间对应关系的误解（Misconception）。学生在数学学习中所出现的许多错误，其实也源于这样语言转换过程中的误解。

比如，在多位数读写过程中，如果读出或用汉字写出“四百三十二万零六十五”，学生在写出相应阿拉伯数字的时候，往往会出现如图2所示的错误。

这样的问题与前面英汉翻译的过程类似，学生潜意识中将“四百三十二万零六十五”看作是一个由“四百三十二”“零”和“六十五”三个元素构成的结构，将三个要素分别翻译为“432”“0”和“65”，而后保持原有顺序依次排列，就得到“432065”。这个过程可以用图3直观地表示出来。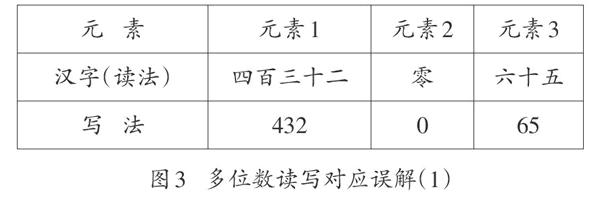

类似的错误极为普遍，比如将“二十一万三千”，写为“2013000”等（见图4）。

这种“一一对应”的误解导致的错误还经常出现在“单位转换”以及钟表上时间读写的过程中，比如将“2.25时”转换为“2时25分”。将“3.2时”转换为“3时2分”等（见图5）。

初学钟表认识的学生会将钟表上直观显示的“时针指向11，分针指向2”，读作或写作“11：02”，同样将“时针指向8，分针指向6”，读作或写作“8：06”。遵循的是视觉上的“意义相同”。

用于数学课程内容表达的语言主要包括文字、图形和符号，学习数学的过程中经常需要进行语言之间的转换，这种转换一旦出现元素数量、元素意义或者元素之间的顺序发生变化的情况，就不符合学生的直觉思考，也就成为容易出现误解和错误的内容。

二、加、减计算中的直觉与误解

类似情况在计算过程中也会出现。比如低年级学生在计算“523+25”时，会出现如图7所示的错误答案。

像“523+25”这样的计算，通常会被教师认为是很简单的，学生出现错误不应该，因为计算过程中并没有出现“进位”的情况。在加法竖式计算中，只有出现进位的情况，才是学生最容易出错的。但在调查中发现，对于低年级学生来说，没有出现进位的“523+25”，相比出现进位的“593+25”，错误率要高。其中的原因就与对应思考中的直觉与误解有关。

学生对于加法计算的经验中，潜意识中至少会有两个理解：第一，加法应当是对至少两个数才可以进行的计算，一个数不能做加法；第二，两个加数的各个数位上的数字应当一一对应。基于这样的理解，当面对“523+25”的竖式时（见图8），其中个位“3+5”和十位“2+2”都顺利计算后，对于孤立存在的“5”就有一种不知所措的感觉。

学生在潜意识中“加法需要两个加数”想法的驱使下，就努力寻找“能够与5做加法的数”。按照就近原则，就可能用到临近的数字“2”，得到“523+25=748”。（见图7a）；也有可能用到临近的数字“4”，就得到“523+25=948”（见图7b）。另外一种可能是认为对于“5”，加法运算没有发生，就会出现“523+25=48”（见图7c）。endprint

相对于出现进位的计算题“593+25”，其中十位数字“9+2”的计算等于11 ，需要向百位进一，此时与学生头脑中“加法需要两个加数”的想法吻合，因此可以顺利地通过“5+1=6”完成计算。因此对一些学生来说，出现进位的“593+25”，相比没有出现进位的“523+25”更符合对应思考中的直觉规律，因此错误率更低。

加法计算中，两个加数位数不同时出现的错误，对于低年级学生来说极其普遍（见图9），一个重要原因是源于对应思考中的误解。这种对应误解产生的错误在减法计算中也同样会出现，比如对于“276-14”，调查发现学生会得到错误结果“162”，原因在于当计算完个位和十位的减法计算后，被减数百位出现孤立的“2”，因此学生在“需要寻找一个减数”想法的驱使下，就会选择临近的数字实现与“2”的减法计算。

综上可以看出，学生许多计算题出现的错误并不是因为“粗心、马虎、不认真”的“算错”，而是依照自己的直觉构建了另外一个题目或算法。比如，在图9中的“84-4=8”，学生在潜意识的直觉中是把“84”看作一个由“8”和“4”构成的结构，而不是“80”和“4”构成的结构，因此学生所完成的计算是“从8和4中减去4”，而不是原题所要求的从“80和4中减去4”。其根本原因在于对于“84”这个符号表达产生了误解。由此也进一步说明低年级儿童认识“位值（Place Value）”其实是相当困难的，困难的原因是与低龄儿童的直觉规律（Intuitive Rule）相违背。凡与直觉规律相违背的内容，通常叫作具有“反直觉”的特征（Counter Intuitive）。

三、文字題中的对应思考

对应思考中的直觉规律也会出现于文字题的解决过程中。比如对于问题：“湖面上有一些天鹅，飞走5只，还剩23只，湖面上原来有多少只天鹅？”教师期望学生列出算式“5+23”，而后计算出结果“28只”。而学生往往直接写出算式和结果为“28-5=23（只）”（见图10）。

事实上，题目所描述的情境在学生头脑中形成了一个由“湖面上原有天鹅”“飞走”“还剩”三个要素构成的结构，而且这三个要素是按照时间先后顺序自然排列的（见图11）。

依据这样的结构，第一个元素是“湖面上天鹅数量”，学生心算出等于28只；“飞走”对应“减号”；“还剩”对应“等号”。因此一一对应地写出算式“28-5=23（只）”。而教师期望的“5+23=28（只）”的写法，打乱了这种保持顺序的对应思考，因此也就违背了学生的直觉规律。

这样的反直觉首先违背了“飞走”和“还剩”的意义，在学生的经验中，这两个词汇都应当与“减少”有关，也就是应当与减法直接相关，而且在问题情境中并没有发生与加法有关的过程，因此学生首先想到的是写出一个减法算式；第二，违背了结构中要素间原有的顺序，学生潜意识中是按照情境中实际发生的顺序书写算式，而教师期望的写法中的顺序与文字叙述的顺序完全不同。因此学生按照自己的直觉所写出来的算式，往往与教师所期望的写法不同，也就不足为奇了，应当视为是另外一种不同的写法，而不是错误的写法。

如今的课堂教学改革，期望从“教为中心”转变为“学为中心”，学生在学习过程中就会依据自己的直觉规律产生多样的想法，其中包括正确的，也包括错误的。这些错误是学生自主学习过程中的必然产物，其中蕴含着的思维规律需要我们认真地去发现和积累，进而真正“读懂学生”。

作为教师应当相信：“错误是必然的，错误是普遍的，错误是有规律的，错误是有用的。”面对学生出现的错误应当采取的态度是“宽容错误，积累错误，研究错误，利用错误”，让错误真正成为教学资源。

（北京首都师范大学初等教育学院 100048）endprint