基于三点估计法的含风电场电力系统无功优化
2017-12-26靳保源
栗 然, 范 航, 靳保源, 张 凡
(华北电力大学新 能源电力系统国家重点实验室, 河北 保定 071003)
基于三点估计法的含风电场电力系统无功优化
栗 然, 范 航, 靳保源, 张 凡
(华北电力大学新 能源电力系统国家重点实验室, 河北 保定 071003)
针对电力系统无功优化时风电出力及负荷的不确定性和相关性,建立一种综合考虑多种不确定因素的无功优化模型。采用三点估计法处理该模型中的不确定因素,将不确定潮流计算转化为较少采样点处的确定潮流计算。为克服花朵授粉算法易陷入局部最优、寻优精度低等不足,将拉丁超立方采样技术、自适应调整转换概率及邻域策略应用于花朵授粉算法,提出一种改进花朵授粉算法求解所建优化模型。在含风电场的IEEE30节点系统上进行仿真测试,结果表明所提无功优化模型和求解方法在不确定环境下能够有效降低系统网损并减小系统状态变量发生越限的风险,从而保证系统的安全经济运行。
无功优化; 风电场; 三点估计法; 花朵授粉算法
0 引 言
电力系统无功优化通过对系统中某些控制变量进行优化配置,可以提高系统电压质量,减少电网有功损耗,是保证系统安全、经济运行的一种有效手段。无功优化属于多约束、非线性的电力系统规划问题[1],求解方法对无功优化的效果有很大影响。早期对无功优化的研究主要集中在算法方面,由此诞生了大量改进算法[2-3]。近年来,风力发电由于其清洁环保、可靠性较高等优点得到大力发展。风电出力具有随机性的特点,风电场的并网将改变电网的潮流分布,给电力系统的运行带来很多不确定因素。此外,实际电力系统运行时,负荷功率的波动是较为常见的现象。系统中存在的不确定因素越来越引起关注,因此研究考虑风电出力和负荷功率不确定性的无功优化问题具有实际意义。
场景分析法是处理不确定性问题较为常用的方法。文献[4]将风电出力处理为几个确定场景及相应概率,对每种场景进行确定性无功优化,最后采用目标函数期望值评估无功配置方案,该方法简单有效,但场景划分方法过于粗糙,不能全面描述风电出力不确定性。文献[5]采用拉丁超立方采样的蒙特卡洛法和场景缩减技术产生若干典型场景,缩减场景后的模型计算精度有所降低,不能精确考虑风电出力不确定。概率潮流作为研究多种不确定因素对系统运行状态影响的有效工具,在无功优化领域已有较多应用。文献[6]建立风电场的概率模型,将量子人工蜂群算法和两点估计法相结合应用到含风电场电力系统无功优化当中。文献[7]建立同时考虑风能、太阳能出力及负荷的随机波动的无功优化模型,采用一种基于全概率公式的概率潮流计算方法求解模型。文献[8]采用基于无迹变换的概率潮流算法处理风电场及负荷功率的不确定性影响。
上述文献仅考虑单一不确定因素对无功优化的影响,或者虽考虑多种不确定因素,却未能考虑不确定因素之间的相关性。实际上同一地区的负荷可能同时增大或减小、邻近的多个风电场风速之间具有较强相关性[9]、风速和负荷间往往存在一定的负相关性[10],这些相关性因素会影响负荷需求特性和电源出力特性,因此有必要综合考虑多种不确定因素以及它们之间的相关性。为处理风电出力和负荷的不确定性及相关性对电力系统无功优化的影响,本文采用能够处理输入变量相关性的三点估计法[11],将不确定潮流计算转化为较少采样点处的确定潮流计算。然后建立以网损期望值最小为目标函数的无功优化模型,采用改进花朵授粉算法进行优化计算,得到确定的优化方案。最后,在含风电场的IEEE30节点测试系统进行仿真测试,验证了本文无功优化方法的有效性。
1 风电场及负荷的概率模型
1.1 风电场概率模型
首先建立风速模型,再得到风电场出力模型。用于模拟风速概率分布的模型很多,本文采用双参数Weibull分布作为风电场风速的概率密度函数:
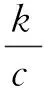
(1)
式中:v为风速;k、c分别为Weibull分布的形状参数和尺度参数。
风电机组输出的有功功率主要与风速的大小有关,两者之间的函数关系可用下式近似描述:
(2)
式中:vin、vr和vout分别为风机的切入风速、额定风速及切出风速;Pr为风电机组额定输出功率;Pw为风机实际输出功率。
为简化计算,本文假设风电场装设的风电机组型号相同,风电场以恒定功率因数控制方式并网运行,且功率因数为1。
1.2 负荷概率模型
本文采用正态分布来描述负荷的不确定性,假设负荷功率因数保持不变,负荷无功功率可由有功功率求出。负荷的概率密度函数表示为
(3)
式中:PL、QL分别为负荷有功功率和无功功率;μ为负荷有功功率期望值;σ分别为负荷有功功率标准差;θ为负荷功率因数角。
2 计及输入变量相关性的三点估计法
目前概率潮流中常用的点估计法由文献[12]提出的Hong点估计发展而来,主要包括2m点估计法(两点估计法)和2m+1点估计法(三点估计法),其中m是输入随机变量个数。文献[13] 通过仿真表明2m+1点估计法比2m点估计法计算结果更精确,且计算量仅多一次潮流计算。文献[11]在2m+1点估计基础上引入基于Cholesky分解的正交变换,所提方法能够有效处理输入随机变量间的相关性,本文采用该方法处理风电出力和负荷的不确定性及相关性。
2.1 三点估计法基本理论
假设X=[x1,x2,…,xm]T为m维输入随机变量,输出随机变量Z与输入随机变量有如下函数关系:
Z=F(x1,x2,…,xm)
(4)
2m+1点估计法对每个输入随机变量取三个采样值,可由下式计算:
(5)
式中:xi,k为输入变量xi的第k个采样值;μxi、σxi分别为输入变量xi的期望和标准差;ξi,k为xi,k的位置系数;λxi,3、λxi,4分别为输入变量xi的偏度和峰度系数。
对于每个采样值xi,k都有一个对应的权重系数wi,k,可由下式计算得到:
(6)
输入变量xi取采样值xi,k,其他变量取均值,可构造一个采样点(μx1,…,μxi-1,xi,k,μxi+1,…,μxm),在该采样点进行确定性计算,得到输出变量Z的一次计算结果,可表达为
Z(i,k)=F(μx1,…,μxi-1,xi,k,μxi+1,…,μxm)
(7)
式中:i=1,2,…,n;k=1,2,3。可以看出,当k=3时,xi,3取均值,则i取值不同,Z(i,3)计算结果相同,因此只需对输出变量Z进行2m+1次计算。
利用权重系数wi,k和Z(i,k),可以得到输出随机变量Z的j阶原点距的估计值:
(8)
式中:E(·)为期望值算子。从上述计算过程可以看出,对于电力系统中的随机变量,不需要知道它们的概率分布,通过历史数据得到它们的均值、标准差、偏度和峰度,便能通过三点估计法得到输出随机变量的概率数字特征。
2.2 输入变量相关性处理
当计及输入变量相关性时,处理方法是将相关随机变量表示为不相关随机变量的线性组合。设输入随机向量X的协方差矩阵CX,对CX进行Cholesky分解,即CX=LLT,得到下三角矩阵L。对L求逆,得到其逆矩阵B,然后对X进行正交变换得到随机向量Y=[y1,y2,…,ym],可表示为
Y=L-1X=BX
(9)
随机向量Y的协方差矩阵CY可由下式计算:
(10)
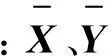
随机变量yi的期望μyi、偏度系数λyi,3和峰度系数λyi,4的计算公式为
(11)
式中:Bij为矩阵B第i行第j列元素。上述步骤将具有相关性的随机变量变换为相互独立的随机变量,并介绍了变换后的随机变量数字特征的求取方法,能够较好地处理输入变量的相关性。
2.3 计算步骤
计及输入变量相关性的三点估计法主要步骤如下:
(1)由输入随机向量X的协方差矩阵CX得到正交变换矩阵B,根据2.2节求取随机向量Y的期望、标准差、偏度和峰度系数。
(2)根据2.1节构造随机向量Y的采样点(μy1,…,μyi-1,yi,k,μyi+1,…,μym)和相应权重wi,k,利用逆正交变换X=B-1Y将Y的采样点变换到X上,得到X的采样点(μx1,…,μxi-1,xi,k,μxi+1,…,μxm)。
(3)利用权重系数wi,k和X的采样点,由式(8)计算得到输出随机变量的各阶距。
3 含风电场电力系统无功优化模型
本文以有功网损期望值最小为目标函数,选定发电机机端电压、并联电容器补偿容量、有载调压变压器变比为控制变量,计及负荷节点电压和发电机无功出力的上下限约束,建立含风电场电力系统无功优化模型。
3.1 目标函数
由于考虑了风电出力及负荷的随机性,使得系统有功网损为随机变量。为有效评估优化配置方案在不确定环境下的优化效果,选取有功网损期望值最小为目标函数:
minf=E(Ploss)
(12)
式中:Ploss为系统有功网损随机变量。
3.2 约束条件
(1)等式约束
等式约束为各节点的有功和无功功率潮流方程,即:
(13)
式中:Pi、Qi和Ui分别为节点i处注入的有功功率、无功功率和节点电压;Gij、Bij分别为节点i,j之间线路电导和电纳;θij为节点i,j电压间相角差。
(2)不等式约束
无功优化模型中不等式约束分为控制变量约束和状态变量约束。
控制变量不等式约束为
(14)
式中:UGi、Tj、QCk分别为发电机机端电压、有载调压变压器变比、并联电容器补偿容量;SG、ST、SC分别为发电机节点集合、有载调压变压器集合、并联电容器节点集合。
状态变量不等式约束为
(15)
式中:Ui、QGj分别为负荷节点电压、发电机无功出力;SD为负荷节点集合。
本文采用智能算法进行优化求解,控制变量在算法中能够满足约束条件。采用罚函数的形式处理状态变量,将原问题转化为无约束问题,增加惩罚项后的目标函数为
minF=E(Ploss)+λ1E(ΔU)+λ2E(ΔQG)
(16)
式中:λ1、λ2为惩罚系数;ΔU、ΔQG分别为电压和发电机无功出力越限随机变量,由下式计算:
(17)
式中:ΔUi、ΔQGj分别为电压和发电机无功出力越限偏差,为非负随机变量。上述过程通过对越限随机变量取期望值并以惩罚项的形式加入到目标函数中,能够保证状态变量满足式(16)中的约束条件。
4 模型求解算法
4.1 花朵授粉算法
受到自然界花朵授粉过程的启发,Yang在2012年提出花朵授粉算法(Flower Pollination Algorithm,FPA)[14]。以最小化问题为例,说明该算法实现过程:
(1)设定算法参数,按式(18)初始化种群。
xij=xjmin+rij(xjmax-xjmin)
(18)
式中:i=1,2,…,n,n为种群规模;j=1,2,…,d,d为解的维数;xij为第i个个体第j维参数;xjmin、xjmax为个体第j维参数的上下限;rij为[0,1]上均匀分布的随机数。
(2)计算个体的目标函数值,将最小的目标函数值作为全局最优值,对应个体为全局最优个体。
(3)如果转换概率p>rand,进行全局授粉,按式(19)更新个体。
(19)
式中:g*为全局最优个体;L是步长,服从Levy分布;α是步长因子以控制步长。
(4)如果转换概率p (20) 式中:xj、xk为种群中的个体,且j≠k;r为[0,1]上均匀分布的随机数。 (5)计算新个体的目标函数值,若新个体的目标函数值更小,则用新个体替代当前个体,否则保留当前个体。 (6)如果新个体的目标函数值比全局最优值更小,则更新全局最优个体和全局最优值。 (7)若满足终止条件则停止运行,输出结果,否则转步骤(3)。 针对FPA算法易陷入局部最优、寻优精度低等不足,本文将拉丁超立方采样(Latin Hypercube Sampling,LHS)技术、自适应调整转换概率,邻域策略应用于FPA算法,提出一种改进花朵授粉算法(Modified Flower Pollination Algorithm,MFPA)。 4.2.1 LHS技术 在求解优化问题之前,如果不知道问题解的位置信息,智能算法中可采取的策略是使初始种群均匀分散在搜索空间上,有利于提高初始种群多样性和算法的全局收敛能力。从式(18)可以看出,FPA算法产生初始种群时先生成[0,1]上均匀分布的随机数,再将随机数映射到搜索空间,这样可能使初始种群只分散在搜索空间的一小部分。为使初始种群均匀地分布于整个搜索空间,MFPA算法采用LHS技术产生d维[0,1]空间上均匀分布的采样点,再将采样点映射到搜索空间生成初始种群。为说明随机采样与LHS的区别,图1给出在二维[0,1]空间上采样24个点的分布图。可以看出,LHS产生的采样点分布更均匀。 图1 两种方法采样点分布图Fig.1 Distribution of sample points by two methods MFPA算法利用采样矩阵替代随机数,初始化式(18)更改为 xij=xjmin+sij(xjmax-xjmin) (21) 式中:sij为LHS技术在d维[0,1]空间上生成的采样矩阵Sn×d中的元素,LHS技术可参考文献[15]。 4.2.2 邻域策略 图2 邻域结构示意图 引入邻域策略后,局部授粉过程中的xj、xk为xi邻域中的个体,且i≠j≠k。通过构建邻域,使得种群中个体更倾向于与自身目标函数值接近的个体传递个体信息,减缓了种群中信息的传递速度,避免了由于粒子间信息传递速度过快而陷入局部最优。 4.2.3 自适应调整转换概率 转换概率p控制着全局授粉与局部授粉之间的转换,p取值大时利于全局寻优,p取值小时利于局部寻优。FPA算法根据种群个体的目标函数值自适应调整转换概率,个体xi的转换概率pi根据自身的目标函数值计算得到,用公式表达为 (22) 式中:pmax,pmin为转换概率最大值和最小值;fi为个体xi的目标函数值;fmax,fmin为当前种群目标函数值的最大值和最小值。可知,目标函数值较小的个体,其性能较好,以较大的概率进行局部细致搜索;目标函数值较大的个体,其性能较差,以较大的概率飞向全局最优,提高自身的性能。 本文测试系统为含风电场的IEEE30节点系统,两个风电场接入节点10。每个风电场包含20台1 MW风电机组,其切入风速、额定风速、切出风速分别为3.5 m/s、13 m/s、25 m/s。风电场以恒定功率因数控制方式并网运行,且功率因数为1。风电场风速Weibull分布的形状参数k为2.11,尺度参数c为9。 设系统负荷功率因数恒定,以测试系统的确定性负荷为均值,标准差为均值的5%。将系统分为两个区域,节点1—15为区域1,节点16—30为区域2,区域内负荷的相关系数为0.9,区域间负荷的相关系数为0.5。两风电场风速之间的相关系数为0.9,风速与负荷之间的相关系数为-0.2。系统控制变量参数见表1。 本文采用所提出的MFPA算法进行优化,惩罚系数λ1=100,λ2=1,算法的参数设置如下:种群规模n=24,转换概率pmax=0.7,pmin=0.3,最大迭代次数maxgen=100,步长因子α=0.7,邻域参数k=3。 表1 控制变量参数 为验证三点估计法有效性,以采样规模为50 000次,能够处理相关性的蒙特卡洛法[17]得到的概率潮流结果作为基准,采用输出变量期望值和标准差的相对误差来评估算法的性能,计算公式为 (23) 两种方法在含风电场的测试系统上进行仿真计,计算得到的网损结果如表2所示,电压幅值相对误差如图3所示。可以看出,三点估计法计算得到的系统网损相对误差很小,电压期望值相对误差小于0.002%,电压标准差相对误差小于0.2%,说明了三点估计法在输入变量具有相关性场合能准确得到输出变量的期望和标准差。 表2 两种方法得到的网损结果 图3 节点电压幅值相对误差 Fig.3 Relative error of bus voltage magnitude 为测试本文所提出的MFPA算法的性能,将其与FPA算法、粒子群算法(PSO)进行比较。三种算法的种群规模和最大迭代次数见5.1节,FPA算法参数参考文献[14],转换概率p=0.8,步长因子α=0.7;PSO算法参数参考文献[18],学习因子c1=c2=2,惯性权重采取线性递减策略,wmax=0.95,wmin=0.4。各算法均独立运行30次,得到统计结果如表3所示,其中网损指式(12)所示有功网损期望值,三种算法30次运行目标函数值的平均值收敛曲线如图4所示。 表3三种算法优化结果对比 Tab.3 Comparison of optimization results by three algorithms 算法网损平均值/MW网损最小值/MW网损最大值/MW网损标准差/MWPSO4.32434.25665.63110.2490FPA4.34094.25634.64620.1048MFPA4.29664.25644.52380.0733 图4 三种算法收敛特性曲线Fig.4 Convergence curve of three algorithms 从表3可以看出,各算法多次运行得到的网损期望的最小值相差不大,但MFPA算法得到的网损期望的平均值、最大值及标准差都优于另两种算法,说明了MFPA算法全局搜索能力较强,多次运行总能找到较好的结果,鲁棒性较好。从图4可以看出,FPA算法在迭代前期具有较快的收敛速度,但容易陷入局部最优;PSO算法和MFPA算法在迭代前期具有相近的收敛速度,但MFPA算法在迭代后期具有更高的收敛精度,能够找到更优的解。 为了测试本文所提出无功优化方法的有效性,将本文方法得到的优化方案与初始方案、传统确定性无功优化得到的优化方案进行对比分析。确定性无功优化中负荷为测试系统确定值,风电出力为期望出力。本文优化方案与确定性优化方案均采用MFPA算法求解,取30次求解中优化效果最好的优化方案。三种方案控制变量的取值如表4所示。 表4 三种方案控制变量取值 在考虑风电出力和负荷的不确定性及相关性条件下,为精确地评估不同方案的优化效果,利用采样规模为50 000的次蒙特卡洛法进行概率潮流计算。各方案的网损概率分布如图5所示,其中初始方案、确定性优化方案以及本文优化方案的网损期望值分别为4.630 4 MW、4.247 2 MW和4.253 5 MW。可以看出,本文优化方案降低系统网损期望值8.14%,说明本文无功优化方法能够有效降低系统网损;此外,确定性优化方案与本文优化方案的网损概率分布非常接近,前者的网损期望值稍小。 图5 三种方案的网损概率分布 Fig.5 Power loss probability distribution of three schemes 各方案的节点电压幅值的分布情况如图6所示,其中圆点代表各节点电压幅值的期望值;折线表示各节点电压幅值的分布区间,下界为电压幅值概率分布的起点,下界为概率分布的终点;黑直线为电压幅值的上限,取值为1.05。可以看出,确定性优化方案的节点电压幅值较高,且有多个节点的电压幅值分布区间越出了约束上限,说明在不确定环境下,确定性优化方案会使系统节点电压有越上限风险;初始方案仅节点12的电压幅值分布区间越出了约束上限,但电压幅值的波动范围较大;本文优化方案仅节点10的电压幅值分布区间越出了约束上限,越限量较小,且电压幅值的波动范围较小,电压较为平稳,基本分布在1.0到1.05之间。 图6 三种方案的电压幅值的分布情况Fig.6 Voltage amplitude distribution of the three schemes 综合网损和节点电压的情况来看,本文优化方案相比于确定性优化方案,以很小的网损代价,很大程度地降低了系统电压越限风险;相比于初始方案,能够有效降低系统网损,电压幅值的波动范围较小,以上分析说明本文无功优化方法的有效性。 本文建立考虑风电出力和负荷不确定性及相关性的无功优化模型,采用能够处理输入变量相关性的三点估计法和改进花朵授粉算法进行求解。 在IEEE30节点系统上进行测试,结果表明三点估计法在计及输入变量相关性时能准确得到输出变量的低阶数字特征,且计算量较小;MFPA算法鲁棒性和全局收敛性能好,具有较好的优化性能和实用性能;本文无功优化方法在不确定环境下能够有效降低系统网损,减小系统状态变量发生越限的风险,从而保证了系统的安全经济运行。 [1] 黄伟,田羽洲.基于新型两阶段混合算法的电力系统无功优化[J].华北电力大学学报(自然科学版),2016,43(1):46-51. [2] 雷敏,杨万里,彭晓波,等.基于改进简化粒子群算法的含DG的配电网无功优化[J].华北电力大学学报(自然科学版),2015,42(1):39-44. [3] 张金环,安海霞,王永春.基于改进小生境帝国竞争算法的多目标电力系统无功优化[J].华北电力大学学报(自然科学版),2014,41(4):41-47. [4] 陈海焱,陈金富,段献忠.含风电机组的配网无功优化[J]. 中国电机工程学报,2008,28(7):40-45. [5] 汪文达,崔雪,马兴,等.考虑多个风电机组接入配电网的多目标无功优化[J].电网技术,2015,39(7):1860-1865. [6] 邓吉祥,丁晓群,张杭,等.基于量子人工蜂群算法的风电场多目标无功优化[J].电测与仪表,2015,52(3):11-17. [7] 王淳,高元海.基于概率统计的含间歇性分布式发电的配电网无功优化[J].电网技术,2014,38(4):1032-1037. [8] 尹青,杨洪耕,马晓阳.含大规模风电场的电网概率无功优化调度[J].电网技术,2017,41(2):514-520. [9] 石东源,蔡德福,陈金富,等.计及输入变量相关性的半不变量法概率潮流计算[J].中国电机工程学报, 2012,32(28):104-113. [10] 张沈习,程浩忠,李珂.考虑相关性的风力发电机组多阶段选址定容规划[J].电网技术,2014,38(1):53-59. [11] MORALES J M,BARINGO L,CONEJO A J,et al.Probabilistic power flow with correlated wind sources[J].IET Generation,Transmission and Distribution,2010,4(5):641-651. [12] HONG H P.An efficient point estimate method for probabilistic analysis[J].Reliability Engineering and System Safety,1998,59(3):261-267. [13] MORALES J M,PEREZ-RUIZ J.Point estimate schemes to solve the probabilistic power flow[J].IEEE Transactions on Power Systems,2007,22(4):1594-1601. [14] YANG X S.Flower pollination algorithm for global optimization[C]//Proceeding of Unconventional Computation and Natural Computation.Berlin:Springer,2012:240-249. [15] 黄煜,徐青山,卞海红,等.基于拉丁超立方采样技术的半不变量法随机潮流计算[J].电力自动化设备,2016,36(11):112-119. [16] 徐斌.基于差分进化算法的多目标优化方法研究及其应用[D].上海:华东理工大学,2013. [17] 陈雁,文劲宇,程时杰.考虑输入变量相关性的概率潮流计算方法[J].中国电机工程学报,2011,31(22):80-87. [18] 熊强.考虑多风电场相关性的场景概率潮流计算及其在无功优化中的应用[D].成都:西南交通大学,2015. Reactive Power Optimization of Power System Containing Wind Farm Based on Three-point Estimation Method LI Ran, FAN Hang, JIN Baoyuan, ZHANG Fan (State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electric Power University, Baoding 071003, China) In allusion to the uncertainty and correlation of wind power output and load in the reactive power optimization of power system, a reactive power optimization model considering a variety of uncertain factors is established. The three-point estimation method is used to deal with the uncertain factors in the model. And the uncertain power flow calculation is transformed into the determined power flow at less sampling points. In order to cope with the local optimum and low optimization precision problems of flower pollination algorithm, a modified flower pollination algorithm is proposed to solve the established optimization model, to which the Latin hypercube sampling technique, adaptive adjustment of switching probability and neighborhood strategy are applied. A simulation is carried out on the IEEE 30-bus system containing wind farm, and the results show that the proposed reactive power optimization model and solution can effectively reduce the power loss and the cross-border risk of system state variables in uncertain environment, thus ensuring the safe and economical operation of the system. reactive power optimization; wind farm; three-point estimation; flower pollination algorithm 2017-01-03. 10.3969/j.ISSN.1007-2691.2017.06.04 TM614 A 1007-2691(2017)06-0020-08 栗然(1965-),女,教授,主要研究方向为新能源与并网技术;范航(1993-),男,硕士研究生,研究方向为电力系统优化运行;靳保源(1992-),男,硕士研究生,研究方向为电力系统分析、运行与控制;张凡(1993-),男,硕士研究生,研究方向为电力系统分析、运行与控制。4.2 改进花朵授粉算法

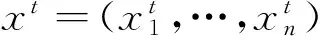

Fig.2 Illustration of neighborhood structure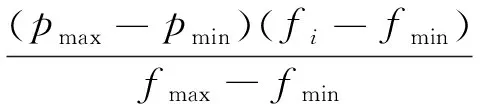
5 算例分析
5.1 测试系统说明
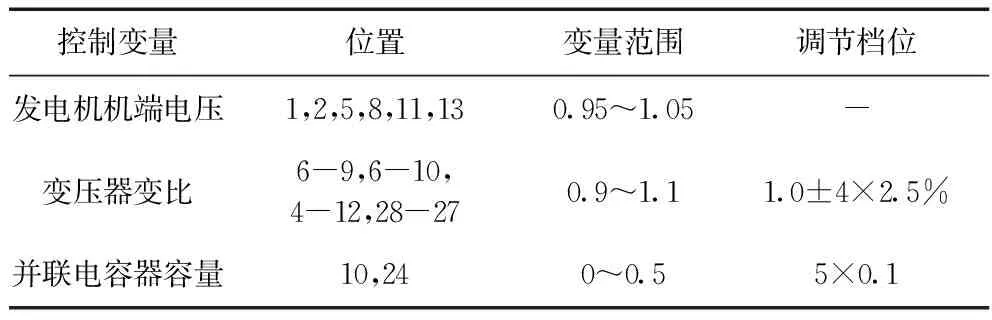
5.2 三点估计法性能测试
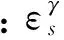
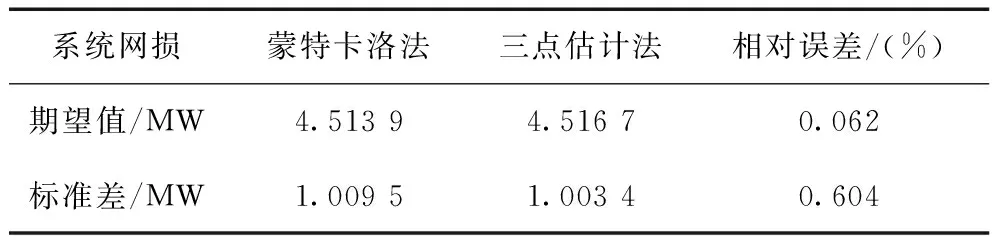
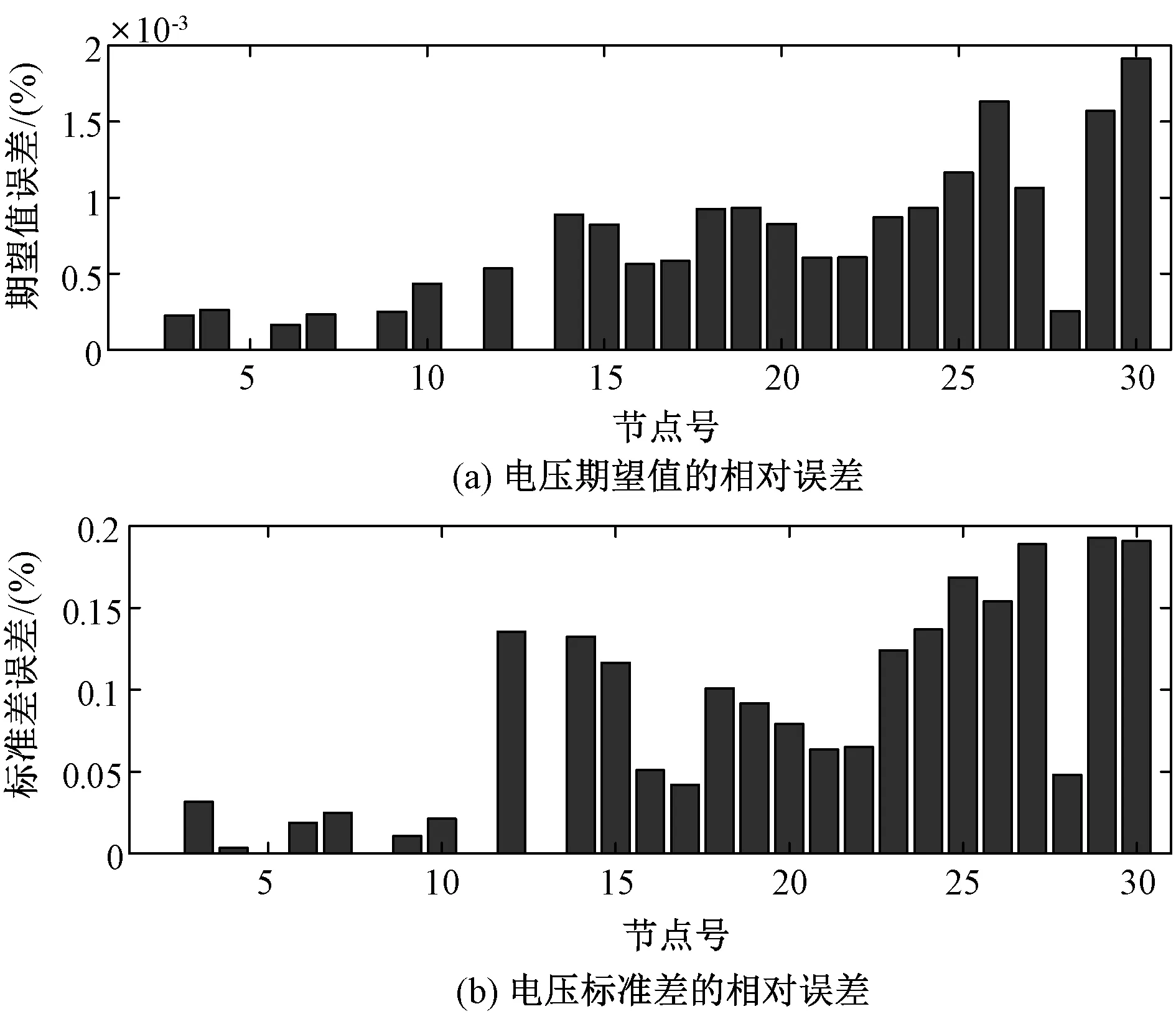
5.3 算法性能测试

5.4 优化效果测试

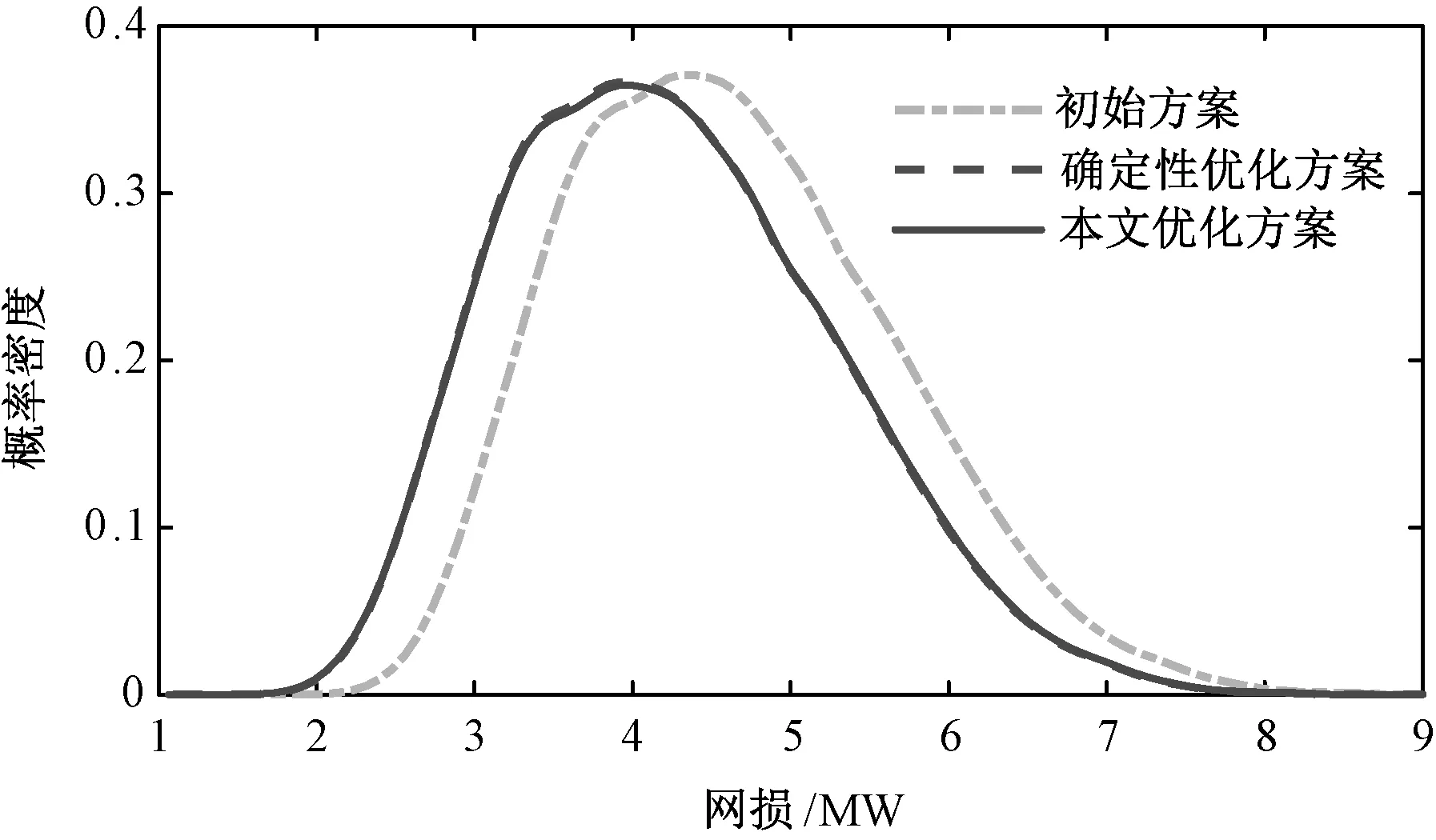
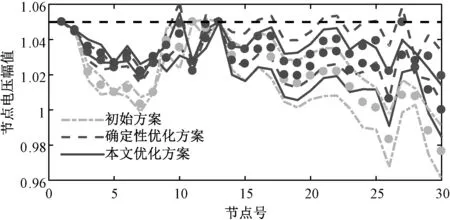
6 结 论
