基于非参数核密度估计和Copula函数的配电网供电可靠性预测

徐玉琴， 张 扬， 戴志辉

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

基于非参数核密度估计和Copula函数的配电网供电可靠性预测

徐玉琴， 张 扬， 戴志辉

(华北电力大学 电气与电子工程学院, 河北 保定 071003)

为了提高配电网供电可靠性预测精度，借鉴Copula函数在可靠性评估方面的应用，提出了基于非参数核密度估计法和Copula函数相结合的配电网供电可靠性预测算法。首先通过考虑线路平均故障率和平均维修时间之间的相关性，采用非参数核密度估计法拟合二者的边缘分布，通过最大似然法估计Copula函数的相关参数；然后采用最小欧式距离进行Copula优选，进而建立线路故障率和维修时间的模型，预测下一年的供电可靠性指标；最后以华东某地供电公司提供的数据为例进行仿真分析。结果表明，该模型能较好地满足供电可靠性预测要求，预测精度高于BP算法。

供电可靠性预测； 非参数核密度估计； Copula函数； 相关性

0 引 言

随着社会经济发展对电能需求不断增加，配电网结构日益复杂的同时对其供电可靠性也提出了更高的要求。可靠性预测为了解电网可靠性发展趋势，确定可靠性投资方向等提供有价值的依据，对系统的运行和维护具有重要的指导意义。

目前，供电可靠性预测一般分为三类：传统法、统计预测法和神经网络预测法。传统法中包括故障模式后果分析法[1]、最小路分析法[2-3]和网络等值算法[4]。传统法大多以准确的配电网结构模型和多年的元件参数作为基准，将配电网等效化简并采用枚举法列举可能失效事件的所有情况，建立故障模式后果表，但对于目前复杂的配电网建模困难，可行性低。统计预测法中一般包括灰色预测法[5]、回归预测法和趋势预测法，通常以历年供电可靠性指标数据为基础进行供电可靠性指标预测，长期预测精度低。神经网络算法通常采用BP算法，通过梯度下降法进行搜索，具有较好的收敛性[6-7]，但BP算法对原始数据要求高且计算速度慢，不易找到最优解。

传统法和统计预测法无法考虑线路故障率和停电持续时间之间所具有的相关性，而神经网络BP算法由于收敛速度慢、容易陷入局部最优解等缺点亦不足以满足可靠性预测快速准确的要求。文献[8]中指出Copula函数能够很好拟合具有相关性的变量；文献[9-10]中指出采用非参数和密度估计和Copula函数的预测模型的预测精度较高。在可靠性方面，文献[11]中首次提出采用非参数核密度估计算法拟合负荷随机变化规律，通过RBTS可靠性测试系统分析计算说明了该方法的有效性；文献[12]提出了基于Copula理论的风光互补发电系统的可靠性评估，通过建立风光出力间的联合概率密度函数，对发电系统的可靠性做出评估。由以上文献中可以看出，采用非参数核密度估计和Copula函数相结合的算法能够很好的解决具有相关性变量的预测问题。

本文借鉴文献[11-12]中的方法，提出了基于非参数核密度估计和Copula函数的供电可靠性预测方法。该方法考虑了线路平均故障率和线路平均维修时间之间的相关性，通过非参数核密度估计得到二者的边缘分布，利用Copula函数建立线路平均故障率和平均维修时间的相关性模型，进而计算下一年度的供电可靠指标。通过对华东某地区供电公司提供的5年线路故障数率和维修时间进行仿真分析，并与基于网架结构的BP算法对比，表明该算法精度更高。

1 供电可靠性评价指标

1.1 供电可靠率

供电可靠率(Reliability On Service)是指在统计期间内，用户有效总供电小时数与统计期间小时数的比值，统计期间通常为一年，RS-1可用以下公式计算：

(1)

1.2 用户平均停电时间

用户平均停电时间(Average Interruption Hours of Customer)是指用户停电时间之和与总用户数的比值，AIHC-1可用以下公式计算：

(2)

2 非参数核密度估计和Copula函数

2.1 核函数定义

非参数核密度估计(Non-parametric density estimation)对数据的分析是完全建立在历史数据上，预先不做任何假设分布，是已知算法中拟合效果最好的方法之一。

假设v1,v2,…vn为研究时段内n个故障时间，其理论概率密度为f(v)，则f(v)的核密度估计为

(3)

式中：h为窗宽系数；n为样本容量；K(·)为核函数；Kh(·)=K(·)/h

2.2 选择核函数

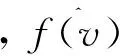
(4)

2.3 选择窗宽

窗宽对核函数具有非常重要的意义，选择好坏直接影响到拟合的精确程度，窗宽太小拟合出来的曲线平滑度差，窗宽太大拟合出的曲线过于平滑而无法反映出数据细节。一般采用经验窗宽法，其表达式如下：

h0=1.06n-1/5σ

(5)

式中：n为样本数；σ为样本标准差。

经验窗宽法的优点在于方便快捷但会带来一定的误差，所以本文采用文献[14]中介绍的方法求取最优窗宽，以达到减小误差提高拟合精确度的目的。具体步骤如下：

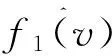
(6)

(3)分别选取服从N(0,1)和N(0,4)的Gauss函数为核函数，结合式(3)和(6)得到下面的最优窗宽模型：

(7)

2.4 Copula函数

Copula函数可将一个N维联合分布问题转换成N个边缘分布和一个联络函数，从而解决了随机变量的边缘分布概率已知而联合概率密度难以求解的问题[15-16]。

2.5 Sklar定理

Sklar定理：令H为随机变量X,Y的联合分布函数，X,Y的边缘分布函数分别为F(x)和G(y)，则存在唯一的Copula函数C，使得下式成立：

H(x,y)=C(F(x),G(y))

(8)

2.6 阿基米德Copula函数

常用Copula函数有正态Copula函数、t-Copula函数和阿基米德Copula函数，前两者具有尾部对称相关系数，无法描述随机变量间的非对称关系。而阿基米德Copula函数既能描述随机变量间对称关系亦能准确的捕捉随机变量间非对称关系，其优良的性能得到了广泛的应用。

阿基米德函数的定义为

C(u1,u2,…uN)=φ-1(φ(u1),φ(u2),…,φ(uN))

(9)

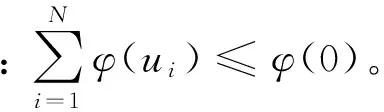
函数φ(u)称为阿基米德Copula函数C(u1,u2,…,uN)的生成元(generator)，满足φ(1)=0且对任意u∈[0,1]。表1列出了一些常用的单参数二元阿基米德函数以及生成元。

表1 阿基米德函数及生成元

由表可知，Gumbel Copula函数具有非对称性，其上尾高，下尾低，即对分布在上尾的变量具有敏感性。Clayton Copula函数下尾高，上尾低对变量分布在下尾部的变化比较敏感，能够捕捉到下尾相关变化。Frank Copula函数适合于具有对称尾部，并且尾部渐渐独立的二元随机变量。

2.7 Kendall秩相关系数

Kendall秩相关系数是衡量变量间相关性的重要指标之一。

设(X1,Y1)，(X2,Y2)相互独立且服从相同分布，P((X1,X2)(Y1,Y2)>0)表示和谐率，P((X1,X2)(Y1,Y2)<0)表示不和谐率两者概率差就是Kendall秩相关系数，即：

τ=P((X1,X2)(Y1,Y2)>0)-

P((X1,X2)(Y1,Y2)<0)

(10)

Kendall秩系数存在说明了变量间具有相关性，由秩相关系数τ可求Copula函数相关参数a。以Frank Copula函数为例，在已知kendall秩相关系数τ的情况下，下式成立：

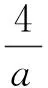
(11)

2.8 欧氏距离

欧氏距离的定义是经验Copula函数和理论Copula函数之间的距离差。其目的是通过对各类Copula函数进行拟合度效验从而选出最优模型。平方欧氏距离表达式如下所示：

(12)

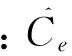
3 基于非参数核密度估计和Copula函数结合的配电网可靠性模型

采用非参数法和Copula函数结合预测配电网供电可靠性大致分为以下几步：

(1) 根据线路平均故障率和平均维修时间的样本，绘制频率直方图。

(2) 选择核函数，通过式(7)分别计算最优窗宽得到式(3)中的核密度估计,即两者的边缘分布曲线。

(3) 根据边缘分布曲线采用最大似然估计法计算不同种类Copula函数的相关参数。

(4) 绘制样本的二元频率直方图，用欧氏距离法选择最优Copula函数。

(6) 计算配电网下一年度的供电可靠性指标。

可靠性建模流程如图1所示。

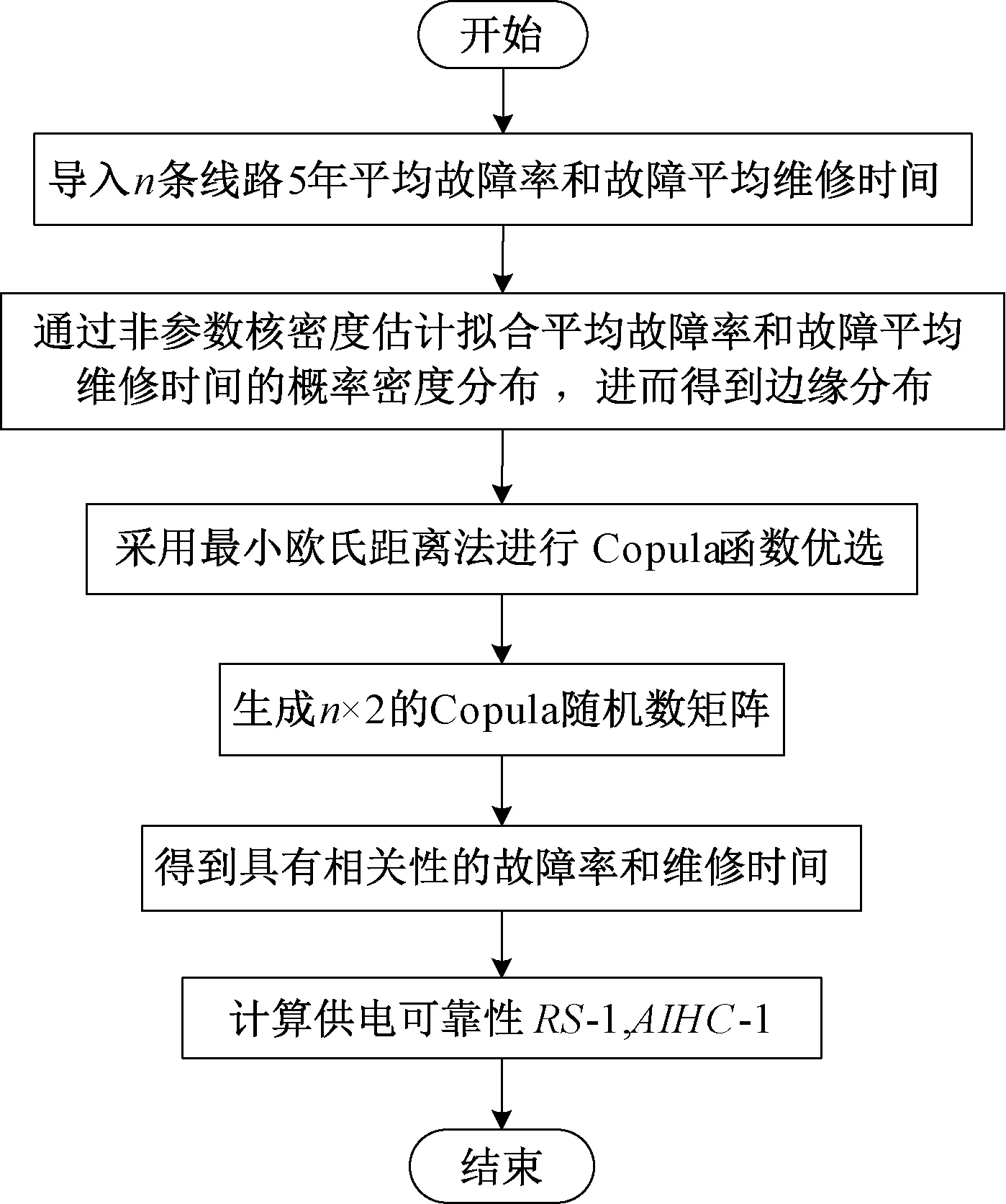
图1 供电可靠性建模流程图Fig.1 Power supply reliability modeling flowchart

4 算例分析

4.1 原始资料处理

本文原始资料取自华东某地区供电公司5年间线路平均故障率和故障平均维修时间，不计及当线路发生故障但重合闸动作成功恢复供电时的次数，因配电网中变压器、断路器、隔离开关损坏次数少，也可以忽略不计。部分原始数据如表2所示。

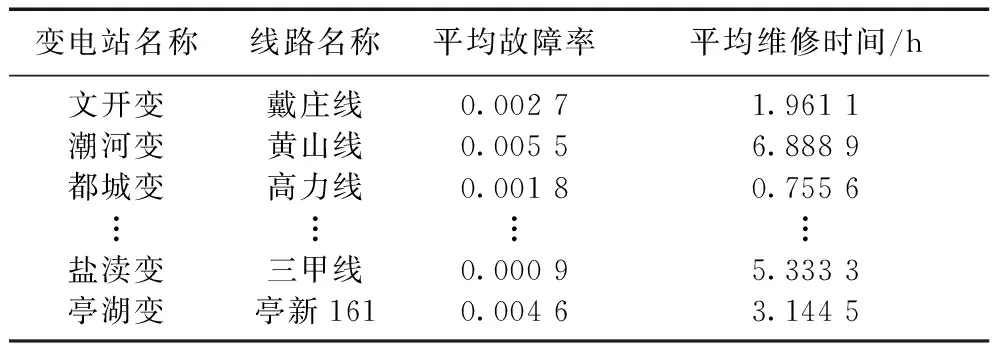
表2 部分原始数据

根据式(11)得到Kendall秩相关系数τ=0.487 5存在，说明变量间具有一定的相关性。

4.2 选择窗宽

根据式(7)分别算出线路平均故障率和平均故障维修时间最优窗宽如表3所示。

表3 最优窗宽

选择最优窗宽是Copula函数优选的基础。

4.3 绘制核密度估计曲线

分别绘制样本数据频率直方图和最优窗宽非参数拟合曲线，以及二元频率直方图如图2、图3所示。由图2可以看出核密度具有很好的拟合性，能够准确的描述历史数据。

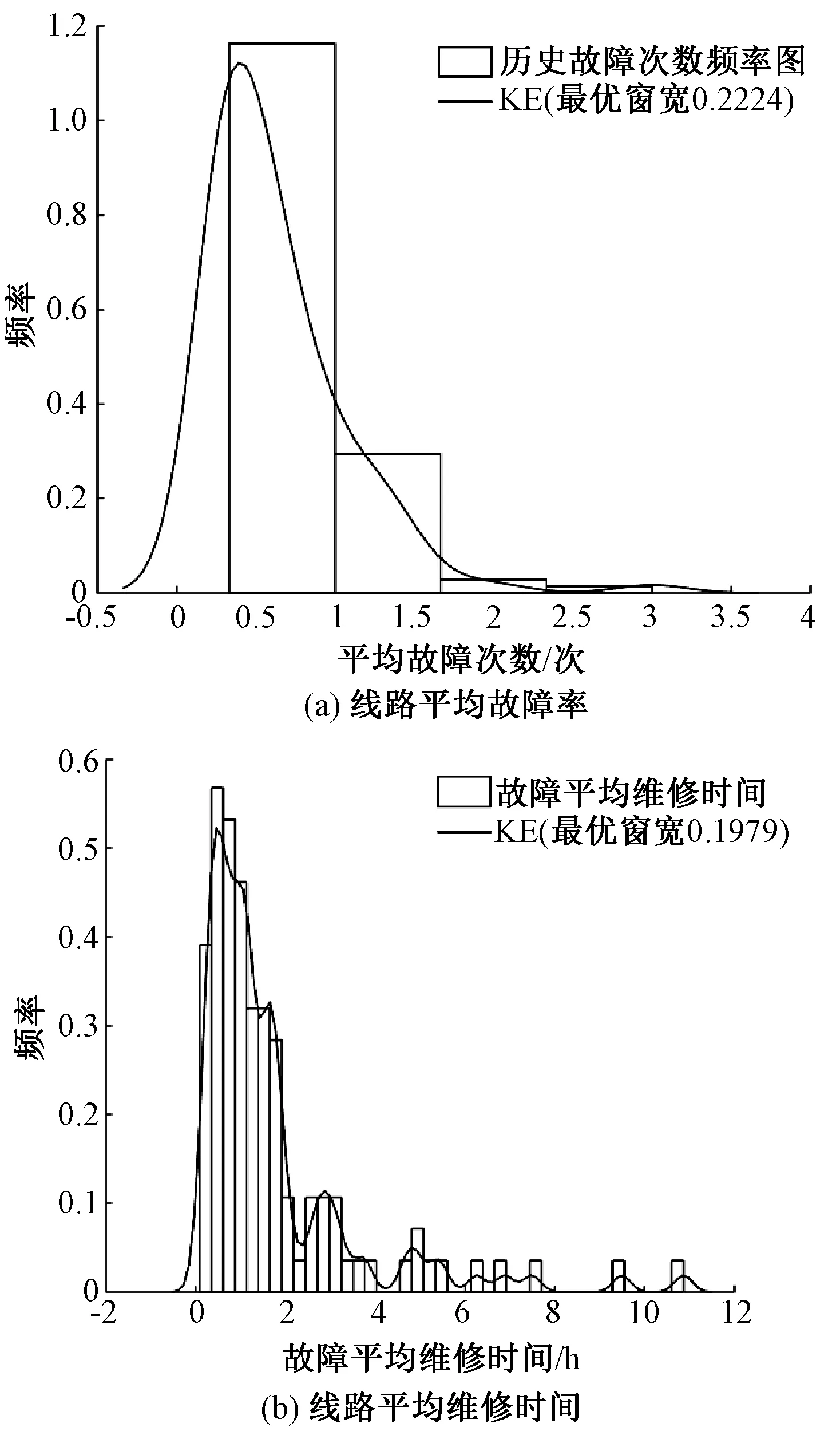
图2 线路核密度估计曲线Fig.2 Kernel density estimation curve of lines

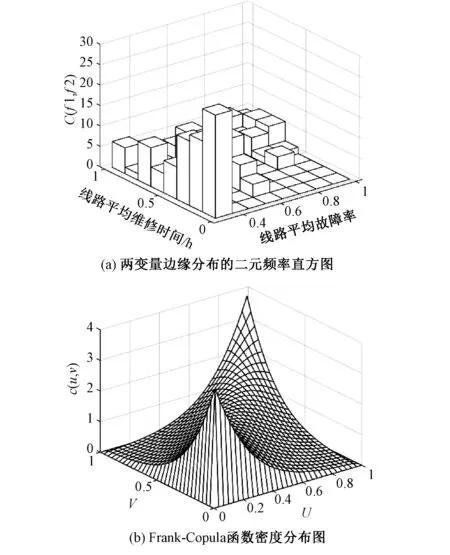
图3 二元分布图Fig.3 Binary distribution

4.4 选择最优Copula函数

由图3，通过直观判断可以看出线路平均故障率和平均维修时间之间的相关性接近于阿基米德Copula函数中的Frank函数。通过最小欧氏距离来验证其是否为最优Copula函数。

根据数据样本，采用最大似然估计法求得各类Copula函数相关系数如下表4所示。由此计算各类Copula函数的欧氏距离。由表5可知，选择Frank-Copula函数是合理的。

表4 Copula相关参数估计

表5 欧氏距离

4.5 生成预测数据

表6 部分预测数据

4.6 计算供电可靠性

根据表6得到的数据预测未来一年配电网供电可靠性，预测和对比结果如表7所示。

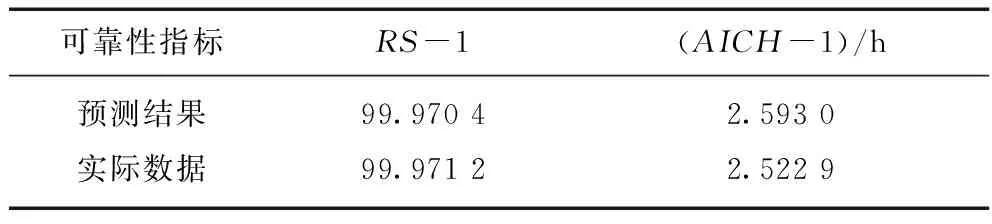
表7 供电可靠性

从数据分析，预测值和实际值之间存在0.000 8%相对误差，该误差在可接受的范围内，说明该方法具有可行性。

4.7 方法对比

将本文所用方法与传统的基于网架结构的BP算法进行对比，算法数据采用文献[17]中的数据，其误差如下表8所示。

表8 方法对比

从表8可以看出，该算法比BP算法具有更好的预测精度。

5 结 论

本文提出了一种基于非参数核密度估计和Copula函数相结合的配电网供电可靠性预测法。与统计算法中直接计算可靠性指标不同，该方法通过建立线路平均故障率和平均维修时间的相关性模型，间接预测供电可靠性指标。以华东某供电公司提供的5年内线路故障数据为例进行仿真分析，结果表明非参数核密度估计能够准确的拟合历史数据，基于Copula函数建立的模型能够真实地反映线路故障率和故障维修时间的相关性。通过与传统BP算法对比，表明了该方法具有更高的预测精度。

[1] XIE Kaigui, ZHOU Jiaqi, BILLINTON R. Reliability evaluation algorithm for complex medium voltage electrical distribution network based on the shortest path [J]. IEE Pro-Gener. Transm Distrib，2003, 150(6):686-690.

[2] 张小娟，李泽荣，张重远，等. 基于最小路法的配电网可靠性评估 [J].电网与清洁能源，2016，26(8):24-28.

[3] 沈宏，付广春. 改进最小路法在配电系统可靠性评估中的应用 [J]. 中国电力，2010，43(10)，20-22.

[4] 万国成，任震，田翔，等. 配电网可靠性评估的网络等值法模型研究 [J]. 中国电机工程学报，2003，23(5)：48-52.

[5] 赖一峰，高亚静. 基于灰色预测改进模型的配电网可靠性指标预测 [J]. 陕西电力，2012，(4)：68-71.

[6] 宋云亭，吴俊玲，彭东，等. 基于BP神经网络的城网供电可靠性预测方法 [J]. 电网技术，2008，32(20)：56-59.

[7] 崔超, 杨婷婷, 刘吉臻, 等. 基于BP网络变量选择与LSSVM结合的锅炉脱硝经济性建模[J]. 中国电机工程学报, 2015, 35(24): 6413-6420.

[8] 蔡菲，严正，赵静波，等. 基于Copula理论的风电场间风速及输出功率相依结构建模 [J]. 电力系统自动化，2013，37(17)：9-16.

[9] 徐玉琴，陈坤，李俊卿，等. Copula函数与核估计理论相结合分析风电场出力相关性的一种新方法 [J]. 电工技术学报，2016，31(13)：92-100.

[10] 卢锦玲，何振民，魏方园，等. 计及风光出力相关性的静态电压稳定概率分析 [J]. 华北电力大学学报(自然科学版)， 2016，43(1)：58-64.

[11] 赵渊，张夏菲，周家启. 电网可靠性评估的非参数多变量核密度估计负荷模型研究 [J].中国电机工程学报，2009，29(31)：27-33.

[12] 赵继超，袁越，傅质馨，等. 基于Copula理论的风光互补发电系统可靠性评估 [J].电力自动化设备，2013，33(1)：124-129.

[13] 陈坤. 计及相关性的风电场出力模型及其应用研究 [D]. 保定：华北电力大学，2016.

[14] 郭照庄, 霍东升, 孙月芳. 密度核估计中窗宽选择的一种新方法 [J]. 佳木斯大学学报, 2008, 26(3): 401-403.

[15] 王小红, 周步祥, 张乐, 等. 基于时变Copula函数的风电出力相关性分析 [J]. 电力系统及其自动化学报,2015, 27(1): 43-47.

[16] 王俊, 蔡兴国, 季峰. 基于Copula理论的相关随机变量模拟方法 [J]. 中国电机工程学报, 2013, 36(22): 75-82.

[17] 黄宇峰. 城市中压配电网可靠性快速评估及预测方法的研究 [D]. 北京：华北电力大学, 2011.

Power Supply Reliability Prediction of Distribution Network Based on Nonparametric Kernel Density Estimation and Copula Function

XU Yuqin, ZHANG Yang, DAI Zhihui

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

In view of the application of Copula function on reliability assessment, this paper proposes an algorithm of power supply reliability prediction of distribution network by combining nonparametric kernel density estimation method with Copula function in order to reach higher accuracy of power supply reliability prediction. Firstly, nonparametric kernel density estimation is used to fit the marginal distribution of average failure rate and the mean time to repair (MTTR) after analyzing the correlation between them. And the relevant parameter of Copula function is estimated by maximum likelihood estimator method. Secondly, based on the optimized Copula function according to the least Euclidean distance criteria, the model of circuit failure rate and MTTR can be established to forecast next year’s power supply reliability indexes. Finally, the paper conducts a simulation analysis by utilizing the data provided by a power supply company in east China. The results show that the proposed model can satisfy the requirements of power supply reliability prediction, and offer more accurate forecasting result than BP method.

power supply reliability prediction; nonparametric kernel density estimation; Copula function; correlation

2017-05-19.

国家自然科学基金资助项目(51367059).

10.3969/j.ISSN.1007-2691.2017.06.03

TM614

A

1007-2691(2017)06-0014-06

徐玉琴 (1964-)，女，教授，主要研究方向为电力系统分析，运行与控制，分布式发电与配电网，电力系统继电保护等；张扬 (1993-)，男，硕士研究生，主要研究方向配网可靠性预测；戴志辉 (1980-)，男，副教授，主要研究方向为电力系统保护，运行与控制，分布式发电与配电网等。