电力线载波通信自适应阻抗匹配电路设计

贾 男， 宋 玮， 王 艳

(华北电力大学 电气与电子工程学院，河北 保定 071003)

电力线载波通信自适应阻抗匹配电路设计

贾 男， 宋 玮， 王 艳

(华北电力大学 电气与电子工程学院，河北 保定 071003)

针对电力线载波通信系统中阻抗失配导致接收端不能有效接收信号的问题，利用Smith圆图和电路变换的原理进行理论分析，提出一种改进的L型结构的阻抗匹配电路来调整输入阻抗，避免了传统L型网络存在匹配禁区的问题，理论分析并推导了匹配电路参数的计算方法，给出了不同阻抗类型所对应区域以及参数的闭式解，最后用仿真验证了计算参数方法的有效性。仿真结果表明，该匹配网络能有效地提高负载侧接收到的功率，和传统需要反复迭代寻优的智能算法相比，匹配速度得到很大的提高。

阻抗匹配； 电力线； Smith圆图； 匹配电路

0 引 言

电力线载波通信是利用现有的输电线路进行数据传输或者语音通信，起始于20世纪20年代初，广泛应用在智能电网监测和控制，具有投资少，见效快，免布线等优点[1]。智能电网作为国家能源发展的战略重点，它的建设离不开智能配电网[2]，配电数据通信网络作为智能配电网建设的关键技术之一，是实现智能配电网的基础条件。随着新的正交频分复用(OFDM)调制技术的发展[3]，基于多载波调制的电力线载波通信技术成为当前全球研究智能配电网通信技术的热点问题。但是对于高频信号而言，电力线环境比较恶劣，网络的输入阻抗呈现复杂的特性，阻抗模值变化可达几kΩ，相角变化接近正负90°，阻抗的变化容易导致阻抗失配进而降低接收端接收到的功率[4]，甚至会导致信号不能有效地传输到接收端，对通信质量造成严重的影响，为了实现从信号源到其负载的最大可能的功率转移，阻抗匹配常常是必需的。而国内外关于电力线阻抗匹配方面的文献较少，是目前亟待解决的问题。任何阻抗匹配设计的首要目标是使负载阻抗“看起来就像”电源阻抗的复共轭值，以使最大的信号源功率转换到负载[5]。目前，关于电力线载波通信自适应阻抗匹配的文献有两类，一类侧重于对网络参数进行优化，在信号源和电力网之间加一个匹配网络，采用常用的智能算法进行参数计算，比如遗传算法[6-8]、量子粒子群算法[9-11]等人工智能算法，这些智能优化算法在理论上能获得较好匹配，而且有较高的可靠性，但是建模复杂，迭代时间长，需要专门的数字处理器，优化结果对初值依赖性较强，容易陷入局部最优，这些对于信号传输是非常不利的。一类侧重于对网络的结构进行分析，比如文献[12]通过改变变压器的匝数和电感值的大小进行阻抗匹配，文献[13]通过改变电容值来实现阻抗匹配，文献[14]提出了VCGIC (Voltage Controlled General Impedance Converter)即用电压来控制电感的通用阻抗变换器来实现阻抗匹配，但是由于使用了运算放大器，该方法对回路中电流有一定的限制。文献[15]进一步提出了具有大电流通过能力的GIC电路。文献[16-19]通过对特定的网络结构采用解析法进行阻抗匹配。上述研究成果对进一步研究阻抗匹配以提高电力线载波通信的传输效率和功率起到了很大的推动作用。

本文在上述研究工作的基础上针对自适应阻抗匹配网络存在的匹配禁区、模型结构复杂、计算量大的问题，借助Smith圆图提出一种新的解析法把输入阻抗和反射系数结合在一起，根据负载的特点进行分类进行阻抗匹配，并对电路中的参数值进行了理论推导，给出了闭式解，最后对该方法进行了仿真对比分析，验证了所提方法的正确性。

1 电力线载波通信自适应调谐系统

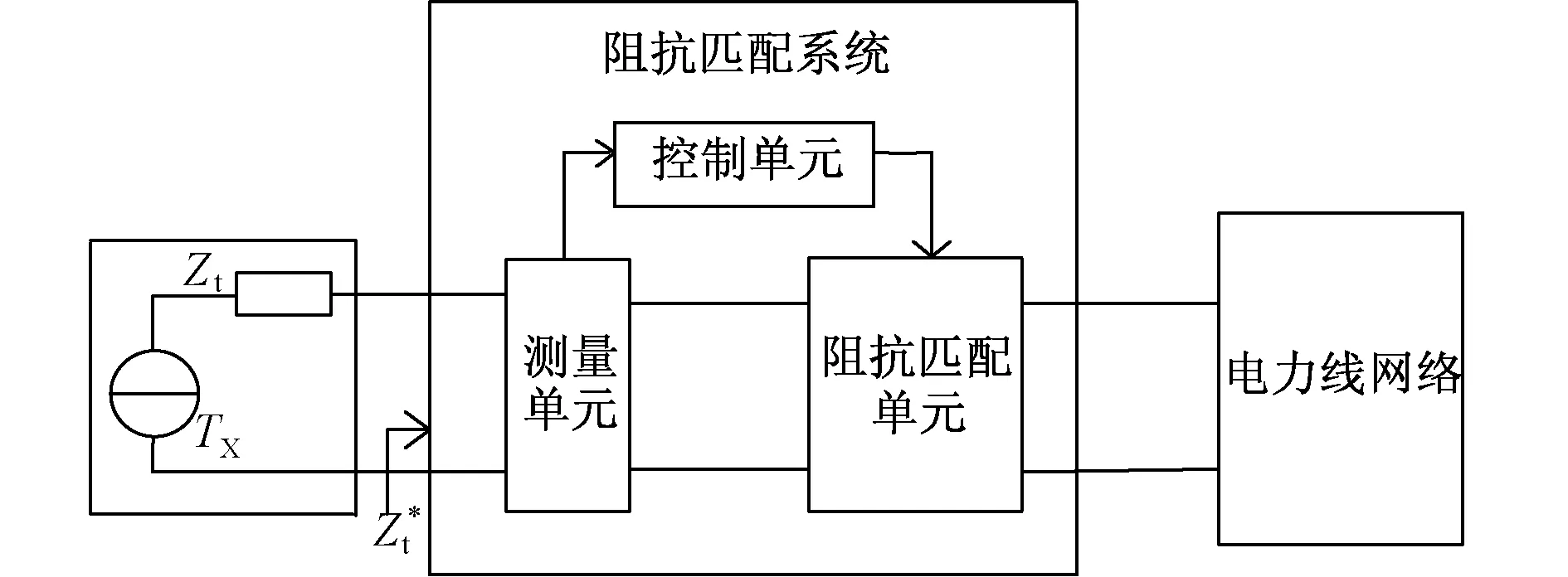
图1 电力线载波通信自适应阻抗匹配系统框图Fig.1 Block diagram of proposed adaptive impedance matching system for the power line communication

阻抗匹配系统模块主要包括测量单元，控制单元和阻抗匹配单元。测量单元包括数据采集单元和逻辑单元，模型如图2所示，数据采集单元用于测量线路的输入阻抗值，电路模型如图3所示，其中运算放大器1测量小电阻两端的电压信号和经过电阻的电流信号，运算放大器2测量输入端与地之间的电压Vs。

图2 测量单元的框图Fig.2 Block diagram of measurement

逻辑单元的输入端为测量得到的电压和电流，输出端为Venv、Ienv、Pact、Bsign；当负载为感性时Bsign=0当负载为容性时Bsign=1，感性负载对应着Smith圆图的上半平面，容性负载对应着Smith圆图的下半平面。控制单元利用测量单元测得的结果来决定匹配单元的的电路结构和需要串并的元件值。

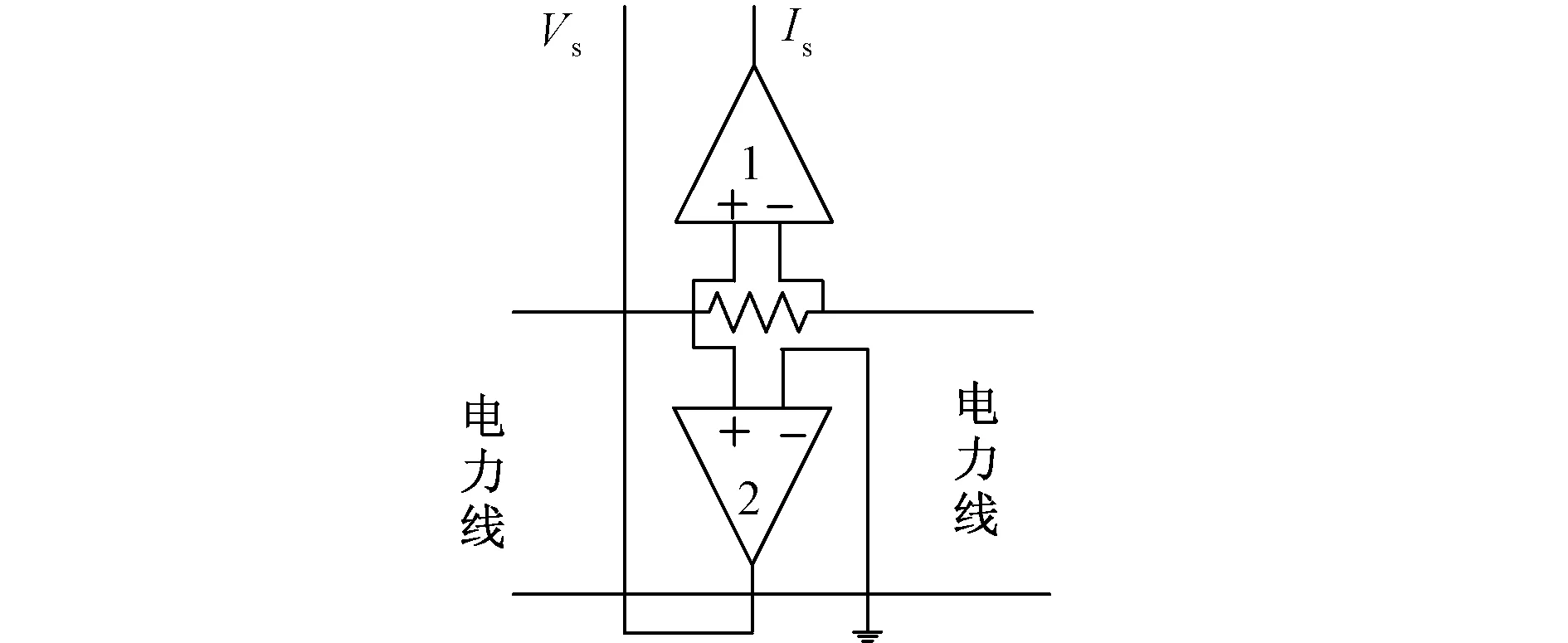
图3 数据采集单元 Fig.3 Circuit level block diagram of sensing unit

2 阻抗匹配网络电路结构及参数的选择

常用的阻抗匹配网络结构有L型、T型和Π型，L型网络结构简单，但是匹配范围存在禁区。针对传统L型网络存在匹配禁区的问题，本文提出一种改进的L型网络，即根据线路阻抗的大小，利用Smith圆图的理论知识，动态选择L型网络的结构和元件的类型，利用解析法来获得元件L、C的参数。

2.1 Smith圆图理论分析

Smith圆图是贝尔实验室的工程师菲利普Smith于19世纪30年代发明的，一经问世就迅速成为一个微波工程是标准的、必备的技能,主要用于射频电路中。根据双导体传输线理论可知：

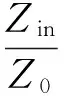
(1)

式中：r表示输入阻抗的归一化电阻；x表示归一化电抗；Z0为信号源内阻；Zin为输入阻抗，ΓL为反射系数。

Smith圆图是反射系数的极坐标图，由等式中的实部和虚部分别相等得

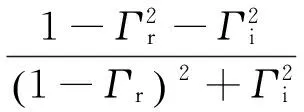
(2)

(3)

其中r∈[0,∞)，x∈(-∞,+∞),Γr,Γi∈(-1,1)。

当阻抗匹配时，Zin=1，即位于Smith圆图的中心。由(2)、(3)可知

(4)

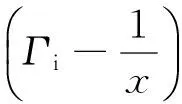
(5)

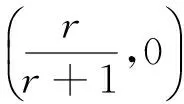
图4 史密斯圆图中的等电阻圆和等电抗圆Fig.4 Equipotential resistance circles and equipotential reactance circle in Smith chart

Smith圆图本质上就是由一系列圆和一系列圆弧组合而成的，将图(4)中的两张图合二为一，就产生了史密斯阻抗圆图。而归一化导纳圆图如图只需在史密斯圆图上把归一化阻抗圆图旋转180°，把这两种圆叠加起来就构成了如图5所示完整的Smith圆图。位于横轴上方的所有弧表示感性负载，位于横轴下方的所有弧表示容性负载，若测得的输入阻抗为r+jx，r和x在Smith圆图上对应的两个圆周的交点值就是该阻抗值对应的反射系数。根据阻抗值在Smith圆图上对应的起始点离等阻抗圆或等电导圆的远近，可以把Smith圆图分为如图5所示的8个区域，不同区域所对应的阻抗值

或导纳范围如表1所示。表中的Venv,Ienv是测量单元测量的电压电流值，Z0为信号源内阻，Zr,Yr为电阻和电导的标幺值。

表1负载阻抗与Smith圆图区域对应关系

Tab.1 Relationship between load impedance and Smith circle area

BsignVenv/Ienv()/Z0Z'r,Y'r区域1≥1<1Z'r≥15Z'r<16Y'r≥18Y'r<170≥1<1Z'r≥14Z'r<13Y'r≥11Y'r<12

2.2 匹配网络的结构分析

图5中a点为匹配前的阻抗值在Smith圆图上所对应的点，a2点为Smith圆图的圆心，圆图内的实线圆代表值为1的等阻抗圆，虚线圆代表值为1的等导纳圆，在等阻抗圆上顺时针移动表示串连一个电感“元件”，而逆时针移动表示串连一个电容“元件”。在等导纳圆上顺时针移动表示并联一个电容“元件”，逆时针移动表示并联一个电感“元件”。阻抗匹配的目的就是通过合适的路径使a点移动到a2点。两元件网络中用了最少的元件即实现了从A点到B点的变化。

阻抗匹配网络并联元件的作用是将一个大阻抗变换成一个小的阻抗，且实部与另一端负载相等，串联元件与其中的电抗分量谐振或抵消，使得电源等效驱动一个与电源电阻相等的负载以实现最大功率转移。

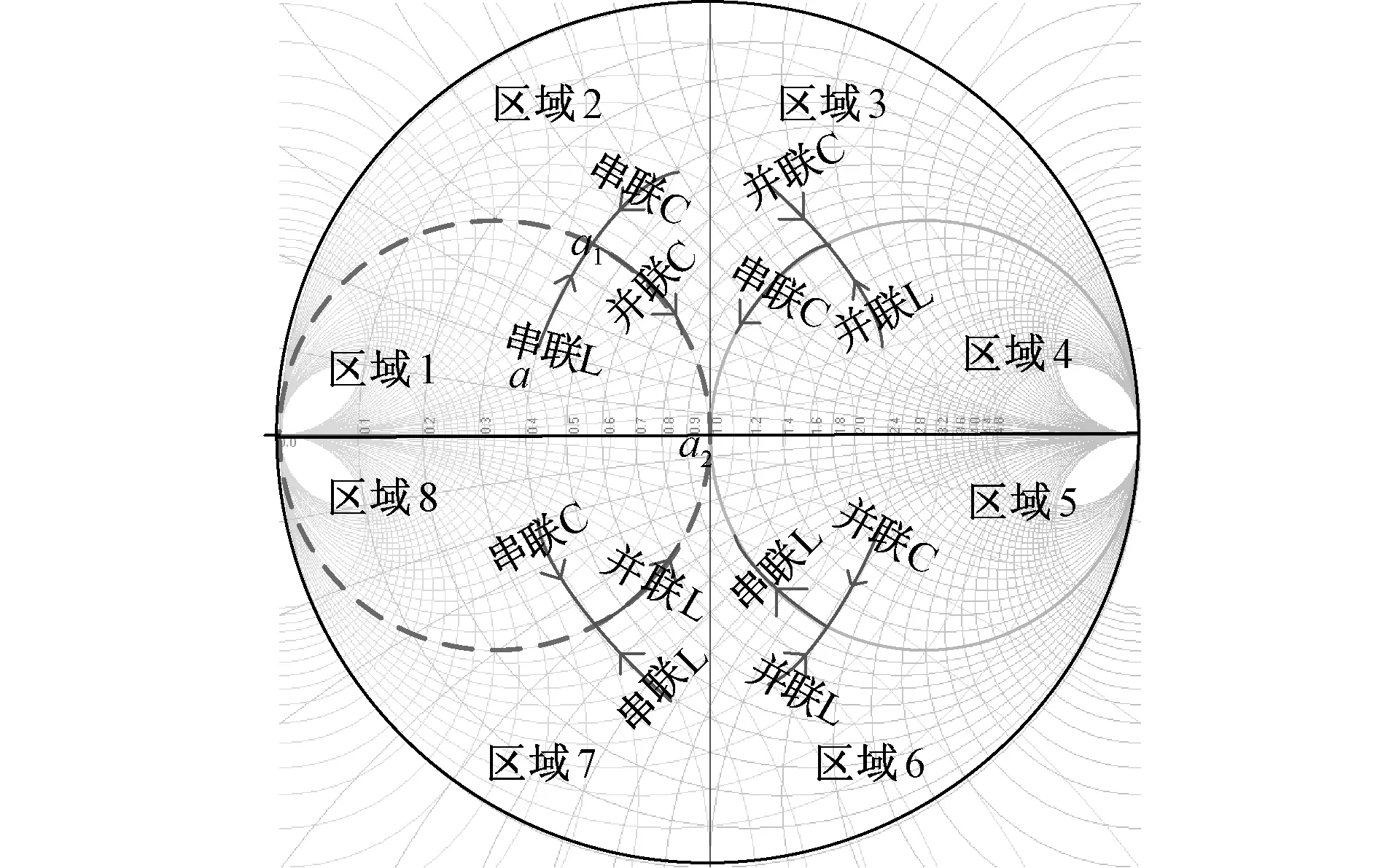
图5 Smith圆图匹配方法和区域分类Fig.5 Smith chart matching method and regional classification

根据上述规律，本文提出的方法是先把电力线负载阻抗从起点匹配到值为1的等电阻圆或者等电导圆上，即从起点移到如图5中虚线和实线所示的等电阻圆或等电导圆上。然后沿着圆回到原点，也就是Smith圆图的圆心。在圆心处负载的阻抗等于信号源内阻的共轭。

不同的区域需要的元件不同，电路结构也不同。根据测量单元测得的线路参数值动态选择匹配电路，避免了传统L型网络存在匹配禁区的问题，传统L型结构匹配电路的匹配范围为Smith圆图的范围的一半，而本文所提的电路结构可以匹配Smith圆图的所有区域。因为接入电路为两个元件，减少了由元件产生的附加损耗，匹配单元的电路结构如图(6)所示，每个区域所对对应的结构如表2所示。电路中的开关S1、S2、S3、S4、S5、S6、S7、S8是由控制单元的8个二进制的比特来控制。

图6 匹配单元的电路结构Fig.6 Circuit structure of matching unit

2.3 元件参数计算方法

以区域1中阻抗为例来分析匹配网络参数的选择，当负载的阻抗值所对应的反射系数在区域1中a点时，对应的匹配方法是：先串联电感，沿着等电阻圆顺时针移动，使点a移动到等电导圆上a1处，然后并联电容，沿着等电导圆顺时针移动，使a1移动到坐标原点即图5中的a2。针对该方法，推导电感电容的计算公式。

如图(5)所示，区域1中的阻抗要想和电源内阻互为共轭，需要先串联电感再并联电容来实现，设a点所对应的电阻为r，电感为x，电导为g，电纳为b，a1点所对应的电阻为r′，电感为x′，电导为g′，电纳为b′ ，则

r′=r,x′=x+x1,g′=1

根据阻抗和导纳的关系可知：

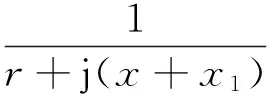
(5)

由于区域1为并联电容，故b′<0。

即x+x1>0

g′=1⟹r=r2+(x+x1)2

(6)

(7)

(8)

由于并联电容后的电纳值为0，即b′+b1=0

(9)

将公式(6)和公式(7)代入公式(9)中得

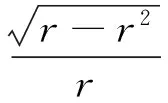
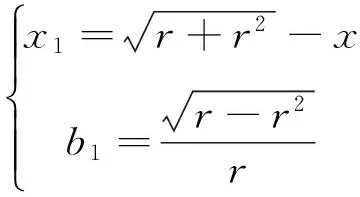
当负载阻抗所对应的反射系数位于其他区域时，参数的求解方法与区域1中的类似，表2给出了匹配时每一步骤需要的元件结构类型和具体值，其中x=2πfl，b=2πfc。

3 仿真分析

电力线载波通信的带宽一般为3～500 kHz,单一频率和固定负载不能验证自适应阻抗匹配的效果，为了验证所提匹配电路模型和参数求解方法的正确性，本节利用Cadence对不同频率下不同负载进行阻抗匹配，仿真时信号源电压为10 V,内阻为50 Ω，阻抗匹配时，信号源发出的功率为1W,负载侧吸收的功率为0.5 W,表3给出了不同频率不同阻抗值进行匹配时按照所提方法所得的元件参数。

图7、8、9给出了匹配前和匹配后负载吸收的功率,仿真结果表明，采用匹配网络后，负载侧吸收的功率得到了大大的提高，基本接近理论的最优值，负载侧效率接近50%，表明该方法能有效地进行阻抗匹配，也进一步体现了所用参数求解方法的正确性。

表2不同区域参数表达式

Tab.2 Different region parameter expressions

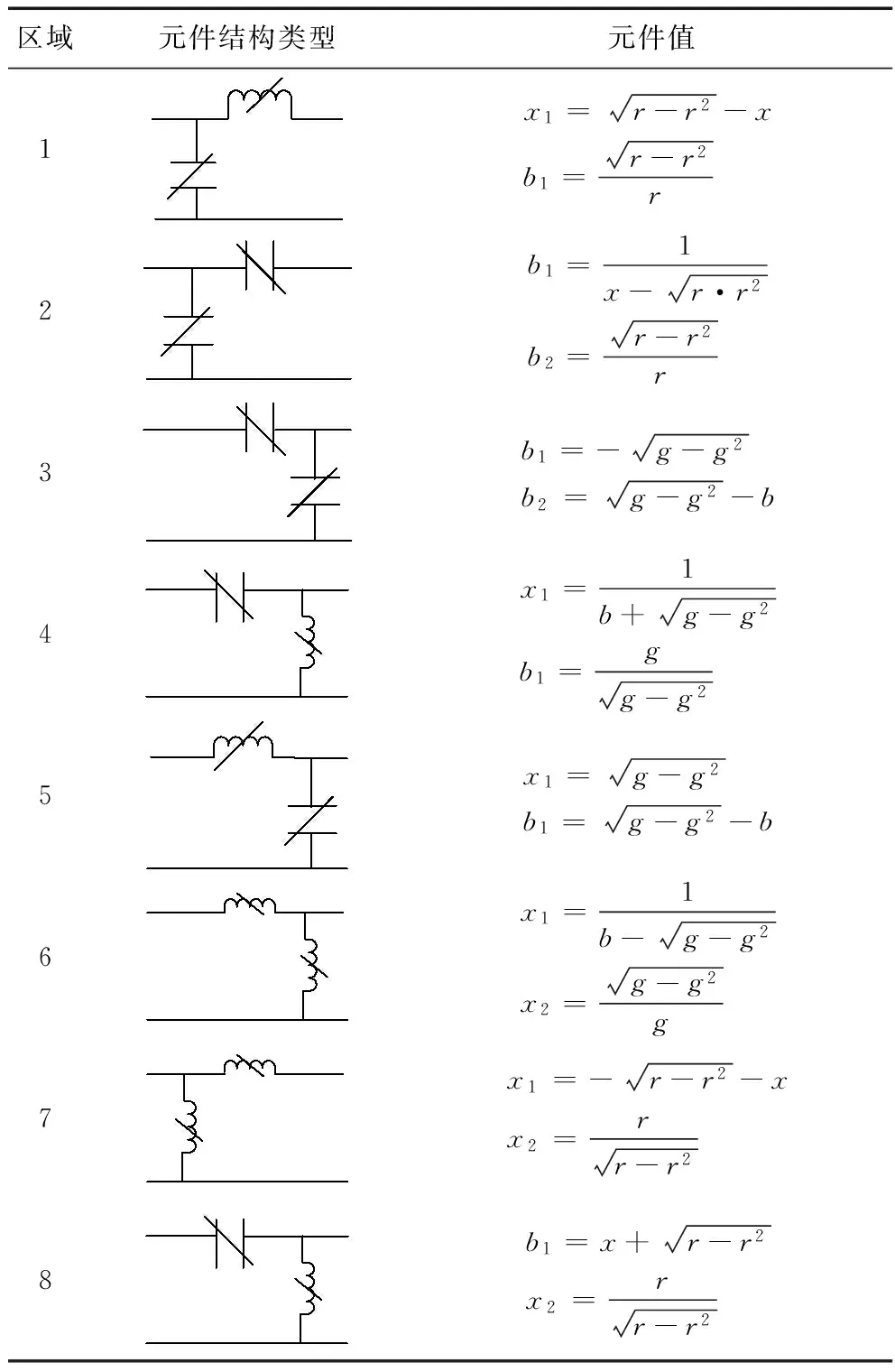
区域元件结构类型元件值1x1=r-r2-xb1=r-r2r2b1=1x-r·r2b2=r-r2r3b1=-g-g2b2=g-g2-b4x1=1b+g-g2b1=gg-g25x1=g-g2b1=g-g2-b6x1=1b-g-g2x2=g-g2g7x1=-r-r2-xx2=rr-r28b1=x+r-r2x2=rr-r2

表3不同频率下不同阻抗值匹配网络对应参数

Tab.3 Different impedance values at different frequencies match corresponding parameters of network

频率/kHz匹配前负载值元件1元件270100-j1008.5nF195.8uH25075-j150913.5pF80.9uH36030+j250400.4pF1.4nF

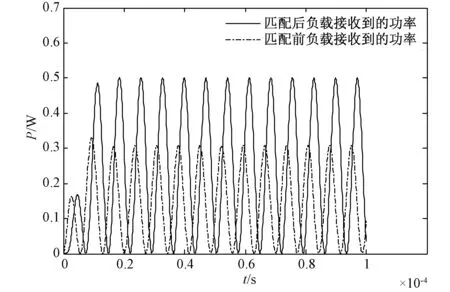
图7 70 kHz时负载吸收的功率Fig.7 Transmission of power from source to network at f=70 kHz

图8 250 kHz时负载吸收的功率Fig.8 Transmission of power from source to network at f=250 kHz

图9 360 kHz时负载吸收的功率Fig.9 Transmission of power from source to network at f=360 kHz

图10给出了在阻抗值为25+j10，仿真参数串联电感值为7.8uH,并联电容之为10.6nF。不同频率下匹配前和匹配后负载吸收的功率，仿真结果表明，采用匹配网络后，负载吸收的功率在一定的频率范围内得到了有效的提高。最佳阻抗匹配发生在300 kHz左右，在离开该匹配中心频点的频率上，阻抗匹配渐渐变差，特别是在400 kHz以后的频段。为了提高带宽，使信号在较宽的频带内都能很好传输，往往需要采用更加复杂的匹配电路，这在后续也需要深入的研究。实际中也可以采用自适应资源分配技术，即信道好的频带上多分配比特，信道条件差的频带内少分比特甚至不进行信号传输来弥补不足，削弱条件差的信道对信号传输的影响，实现电力线在3～500 kHz的窄带范围内可靠传输。

图10 负载在不同频率下吸收的功率Fig.10 Transmission of power from source to the network at different frequencies

传统的智能算法需要经过几十次搜索迭代过程才能达到阻抗匹配，这远远不能达到通信系统中对实时性的要求，为了验证所提方法的快速性，采用和文献[10]中相同的仿真条件进行比较，本文所提的解析法和遗传算法，粒子群算法在阻抗匹配时都能有很好的匹配度，负载侧接收到的功率都能接近最优，但是达到最优所需的时间差别很大，表4给出了不同方法所对应的迭代次数和时间。遗传算法需要迭代60次，寻优时间为1.54 s,改进粒子群算法需要迭代25次，寻优时间为25 ms,而本文所采用解析法给出了最优时的闭式解，避免了大量的反复迭代过程，寻优时间仅为28.5 us,远远小于传统智能算法所需要的时间。

表4 不同算法所寻优时需要的时间

4 结 论

本文利用Smith圆图和电路变换原理，针对L型网络虽然结构简单但是存在匹配禁区，传统智能算法迭代寻优过程所需时间长的问题，提出了改进的L型网络进行自适应阻抗匹配。给出了匹配网络单元电路的等效模型，并对参数的求解方法进行了理论分析和推导，给出不用类型阻抗值所对应参数求解方法。本文用仿真验证所提阻抗匹配网络模型和参数求解方法的正确性。与传统算法相比避免了复杂的迭代过程，能在更短的时间内实现阻抗匹配。通过对匹配网络进行扫频分析，匹配效果在离开中心频点的频率上渐渐变差，比较适合窄带传输，在很宽的频带内完全匹配，后续需要深入研究。

[1] 段瑞超,翟峰,陆俊,等. 基于公平因子的宽带电力线OFDM统跨层资源分配[J]. 现代电力,2015,32(4):79-84.

[2] 王东,王艳,焦彦军,等. 基于局部反射理论的中压配电网电力线通信信道建模法[J]. 电力系统自动化,2017,36(2):178-183.

[3] 李春阳,黑勇,乔树山. OFDM电力线载波通信系统的定时同步和模式识别[J]. 电力系统自动化,2012,36(8):58-60.

[4] 郭以贺. 中压电力线通信关键技术研究[D].保定：华北电力大学,2014.

[5] 李平辉. 射频电路设计[M]. 北京：电子工业出版社，2015.

[6] THOMPSON M， FIDLER J K. Application of the. genetic algorithm. and simulated annealing to LC filter tuning[J] IEE Proc. Circuits, Devices and Systems, 2002,148(4): 177-182.

[7] 范函,张浩. 一种电力线载波通信自适应阻抗匹配方案[J]. 电力系统保护与控制,2009,37(8):79-82.

[8] TAN Y H,SUN Y C，LAUDE R D. Automatic impedance matching and antenna tuning using quantum genetic algorithms for wireless and mobile communications[J]． IET Microwaves， Antennas & Propagation， 2013，7(8): 693-700．

[9] 肖元强,曹敏,李川,等. 基于PSO的低压电力线载波通信阻抗自适应匹配[J]. 中国电力,2014,47(1):133-137.

[10] 宋建立,谭阳红,张海霞,等. 基于QPSO算法的电力载波通信自适应阻抗匹配[J]. 计算机工程与应用,2015,51(1):228-233.

[11] 杨晓博,李阳,肖朝霞,等. 改进粒子群算法的自动阻抗匹配技术[J]. 重庆大学学报,2016,39(6):41-48.

[12] QI L SHE J, FENG Z. Adaptive impedance matching in power line communication[C]//2004 Microwave and Millimeter Wave Technology, 2004 ICMMT 4th International Conference on Proceedings,Nanjing,China, 2005:887-890.

[13] CHOI W H, PARK C Y.A simple line coupler with adaptive impedance matching for Power line Communication[C]//2007 IEEE International Symposium on Power Line Communications and Its Applications, Pisa,Italy,2007:187-191.

[14] PARK C Y, JONG K A, CHOI W H.Coupling circuitary for impedance adaptation in power line communications using VCGIC[C]//2008 IEEE International Symposium on Power Line Communications and Its Applications, Jeju,South Korea, 2008:293-298.

[15] SUN Y H, AMARATUNGA G A J. High-current adaptive impedance matching in narrowband power-line communication systems[C]//2011 IEEE International Symposium on Power Line Communications and Its Applications (ISPLC), Udine,Italy,2011: 329-334.

[16] 李阳,张雅希,闫卓,等. 磁耦合谐振式无线电能传输系统阻抗分析与匹配电路设计方法[J]. 电工技术学报,2016,(22):12-18.

[17] 艾慧,谭阳红,何怡刚,等. 自动调谐系统阻抗匹配网络解析法[J]. 电子测量与仪器学报,2016,(2):283-290.

[18] GU Q, LUIS J R D, MORRIS A S, et al. An analytical algorithm for pi-network impedance tuners[J]. IEEE Transactions on Circuits Systems I Regular Papers, 2011,58(12):2894-2905.

[19] VAN Bezooijen A, DE Jongh M A, VAN Straten F, et al.Adaptive impedance-matching techniquesfor controlling L networks[J]. IEEE Transations on Circuits Systems I Regular Papers,2010,57(2):495-505.

Design of Adaptive Impedance Matching Network in Power-line Communication

JIA Nan, SONG Wei, WANG Yan

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

In view of the receiving terminal’s failure of effectively receiving signals in the power line communication system due to impedance mismatch, based on a theoretical analysis of the problem by means of the Smith chart and the principle of circuit transformation, this paper proposes an improved L-shaped impedance matching circuit to adjust the input impedance and to avoid the existence of match forbidden zone in traditional L-type network. The calculation method of matching network parameters is theoretically analyzed and deduced. Additionally, this paper also provides closed solutions of the corresponding regions and parameters of different impedance types and the effectiveness of the method is verified by simulation. The simulation results show that the matching network can effectively improve the power

on the load side. Compared with the traditional intelligent algorithms which need iterative optimization, the matching speed is greatly enhanced.

impedance matching; power line communication; Smith chart; matching circuit

2017-03-20.

10.3969/j.ISSN.1007-2691.2017.06.09

TM711

A

1007-2691(2017)06-0054-07

贾男(1991-)，女，硕士研究生，主要从事电力线载波通信等方面的研究;宋玮(1963-)，男，教授，主要从事电力系统及其自动化、电力线载波通信等方面的研究。

doi:10.3969/j.ISSN.1007-2691.2017.06.10