二端口分数阶变类器及其电路仿真研究
2017-12-26梁贵书单栋清
梁贵书, 马 龙, 单栋清
(华北电力大学 电气与电子工程学院,河北 保定 071003)
二端口分数阶变类器及其电路仿真研究
梁贵书, 马 龙, 单栋清
(华北电力大学 电气与电子工程学院,河北 保定 071003)
应用分数阶微积分理论对传统整数阶二端口变类器进行拓展。建立了分数阶变类器的统一模型,给出了12种分数阶变类器赋定关系及传输矩阵表达形式,实现了I型分数阶Cα-R、Lβ-R和Mα,β-R变类器。最后,通过Multisim电路仿真对所提实现形式进行了验证。
分数阶微积分; 变类器; 二端口网络; Multisim电路仿真
0 引 言
在电路理论中,最早定义的基本元件包含电阻、电容和电感三类,分别通过电压—电流关系、电荷—电压关系和电流—磁链关系进行定义。1971年,文献[1]从公理完备性角度入手,指出存在由电荷—磁链关系定义的第四类元件,并称其为忆阻元件。后来文献[2]在研究中发现,基于上述四类元件对电路进行描述时存在一些无法克服的问题,因此在1980年对公理化二端口元件定义方法进行了拓展,提出了高阶和混合元件[3],解决了非线性器件造型问题的同时极大的丰富了传统电路中的元件。
元件的独立性在一定程度上阻碍了电路理论的发展[4],设计和提出一种网络实现不同类型的二端元件的转换显得十分重要,尤其是在无穷多种高阶元件的概念提出之后,实现元件类别转换的重要性更为突出。为此,文献[4]首先提出了变类器、反照器以及变标器的概念来解决非线性电阻、电感和电容的实现问题,给出了L-R、C-R和L-C三种变类器的符号表征、传输矩阵以及含受控源的基本实现电路;文献[5]中定义了两类新的L-R变类器,并给出了基于第二代电流传送器的电路实现形式;文献[2]中给出了I型和II型共计12种二端变类器的赋定关系;文献[6]中将变类器用于高阶元件的变换,给出了高阶元件变类器对应的赋定关系、传输矩阵及基本的电路实现形式;文献[7]中在已有的变类器基础上,又提出了新类型的L-R、C-R和L-C变类器,并通过电流传送器进行实现;文献[8]中给出了一种用于忆阻、忆感和忆容相互变换的通用变类器结构。
近几十年来,分数阶微积分理论的快速发展为人们提供了一种解释复杂现象、过程和动态系统的强大工具[9]。在电气工程领域中,已有变压器分数阶建模[10,11]、电缆分数阶建模[12]、DC-DC变换器分数阶建模[13]、超级电容器分数阶建模[14]的相关报道。研究表明,采用分数阶模型能够更为简洁准确地描述电气工程领域中集肤效应和介质材料的频变特性,因此电气设备的分数阶建模备受关注。在建模过程中,学者们提出了分抗元件[15]的概念,这类元件的赋定关系中包含电压或电流的任意阶微分运算,从而极大地拓展了传统电路元件的范畴。可以看到,已有的整数阶电阻、电容和电感分别对应分数阶元件阶次为0,-1和+1的情况。后来,人们又提出了分数阶耦合电感[16]、分数阶双口元件以及分数阶高阶元件[17]的概念。可以看到,随着研究的深入,越来越多的分数阶元件将出现在人们面前。此外,尽管国内外学者对分数阶元件的实现进行了大量研究[18-20],但由于分数阶元件种类繁多,制造过程复杂,任意阶次的分数阶元件的制造目前仍无法解决。而另一方面,随着分数阶电路的稳定性[21]、时频域分析[9]、灵敏度分析[22]等问题研究的深入,人们对分数阶元件的需求会越来越迫切。提供一种借助已有或易于制造的分数阶元件,来获得未知的或难于制造的分数阶元件就显得尤为必要。
因此,本文开展分数阶变类器的研究,旨在实现分数阶元件类别的转换。通过分数阶微积分的引入,获得分数阶变类器的统一模型,推导获得12种变类器的赋定关系和传数矩阵表达形式,给出了I型分数阶Cα-R、Lβ-R和Mα,β-R变类器的电路实现,并通过Multisim进行了仿真验证。
1 分数阶微积分与分抗元件
1.1 分数阶微积分定义
分数阶积分定义[9]为
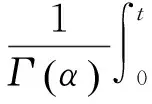
(1)
式中:D-α为分数阶微分算子;α为任意正数;Γ(·)为欧拉伽玛函数。
Caputo分数阶微分定义[9]为
(2)
式中:n-1<α≤n,Dα为分数阶微分算子,函数f的n阶导数f(n)在区间[a,t]可积。
1.2 分数阶元件定义
分数阶电容[9]的特性方程为
iα(t)=CαDαuα(t)
(3)
式中:Cα为分数阶电容的电容值,F/s1-α。
分数阶电感[9]的特性方程为
uβ(t)=LβDβiβ(t)
(4)
式中:Lβ为分数阶电感的电感值,H/s1-β。
分数阶忆阻[24]的定义为
Dβi(t)=Mα,βDαu(t)
(5)
式中:当β=0,α=0时,Mα,β为电阻;β=1,α=0时,Mα,β为电容倒数;β=0,α=-1时,Mα,β为电感;β=1,α=-1时,Mα,β为忆阻。更一般的取值,式(5)表示分数阶元件。
2 二端口分数阶变类器
2.1 分数阶变类器原理及赋定关系
在传统电路理论中,I型和II型的整数阶双口(a1,b1)-(a2,b2)变类器[3]的赋定关系分别由式(6)、(7)给出:
(6)
(7)
式中:a1,b1,a2和b2均为整数。
随着分数阶微积分理论的发展,人们意识到很多情况下将微分和积分限定为整数,存在很大的局限性。解除对参数a1,b1,a2和b2的整数限制,可以获得分数阶次的变类器。本文采用图1所示的电路符号表示分数阶变类器,其中X和Y表示不同类型的分数阶元件,K表示分数阶变类器的类型,FOE表示变类器中的分数阶元件。

图1 分数阶变类器电路符号Fig.1 Circuit symbol of fractional mutators
在图1中,当端口2外接元件Y时,从端口1看进去的等效元件为X;同理端口1外接元件X时,从端口2看进去的等效元件为Y。从而方便地实现了分数阶元件之间的相互转换。根据所实现类型变换的不同,可以将分数阶变类器细分为Cα-R、Lβ-R、Lβ-Cα、Mγ,ν-R、Mγ,ν-Lβ和Mγ,ν-Cα六类,每一类包含Ⅰ型和Ⅱ型两种,表1和表2分别给出了Ⅰ型和Ⅱ型分数阶变类器的赋定关系和端口指数。本文中重点研究I型分数阶变类器,Ⅱ型分数阶变类器可采用本文给出的方法类似地进行研究。
表1I型变类器赋定关系及端口指数
Tab.1 Constitutive relations and port indexes of type I mutators

类别赋定关系端口指数Cα-Ru1=u2,i-α()1=-i20,-α()-0,0()Lβ-Ru-β()1=u2,i1=-i2-β,0()-0,0()Lβ-Cαu-α()1=u2,i1=-i-β()2-α,0()-0,-β()Mγ,ν-Ru-γ()1=u2,i-ν()1=-i2-γ,-ν()-0,0()Mγ,ν-Lβu-γ()1=u-β()2,i-ν()1=-i2-γ,-ν()--β,0()Mγ,ν-Cαu-γ()1=u2,i-ν()1=-i-α()2-γ,-ν()-0,-α()
表2Ⅱ型变类器赋定关系及端口指数
Tab.2 Constitutive relations and port indexes of type Ⅱ mutators

类别赋定关系端口指数Cα-Ru1=-i2,i-α()1=u20,-α()-0,0()Lβ-Ru-β()1=-i2,i1=u2-β,0()-0,0()Lβ-Cαu-α()1=-i-β()2,i1=u2-α,0()-0,-β()Mγ,ν-Ru-γ()1=-i2,i-ν()1=u2-γ,-ν()-0,0()Mγ,ν-Lβu-γ()1=-i2,i-ν()1=u-β()2-γ,-ν()--β,0()Mγ,ν-Cαu-γ()1=-i-α()2,i-ν()1=u2-γ,-ν()-0,-α()
2.2 分数阶Cα-R变类器
根据表1中给出的分数阶Cα-R变类器的赋定关系,借助分数阶元件、受控源、电阻元件可以实现分数阶Cα-R变类器。图2和图3中分别给出了含分数阶电容和分数阶电感实现的Cα-R变类器的电路结构。以图2为例,根据KCL和KVL定理,获得电路方程为
(8)
对式(8)整理可得:
(9)
式(9)与表1中Cα-R的赋定关系相同,可知该电路可实现分数阶电容与电阻的相互变换。类似地,对图3中的电路进行分析,可得到相同的结果。
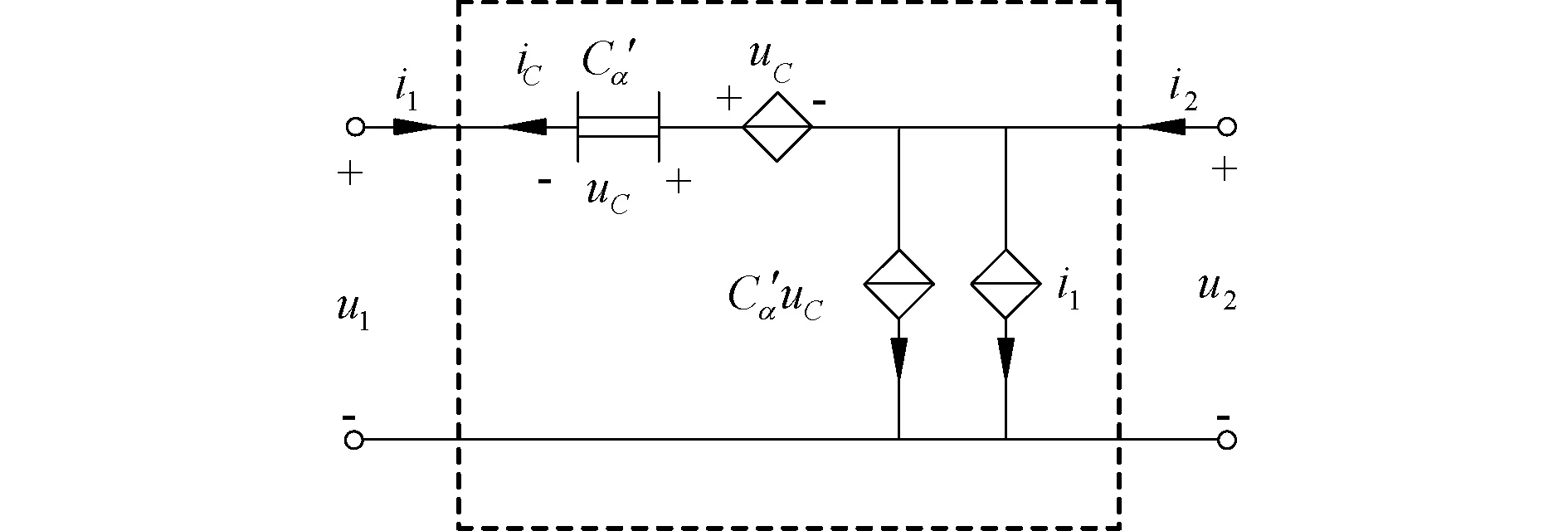
图2 含分数阶电容的Cα-R变类器Fig.2 Cα-R mutator with a fractional capacitor
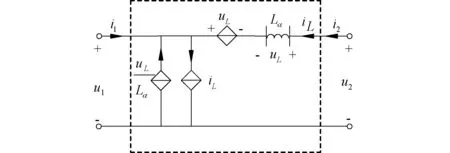
图3 含分数阶电感的Cα-R变类器Fig.3 Cα-R mutator with a fractional inductor
2.3 分数阶Lβ-R变类器
图4和图5中分别给出了含分数阶电容和分数阶电感实现的Lβ-R变类器的电路结构。
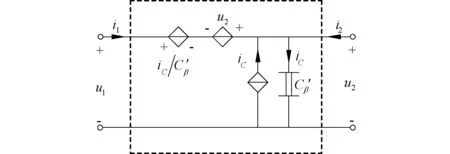
图4 含分数阶电容的Lβ-R变类器Fig.4 Lβ-R mutator with a fractional capacitor
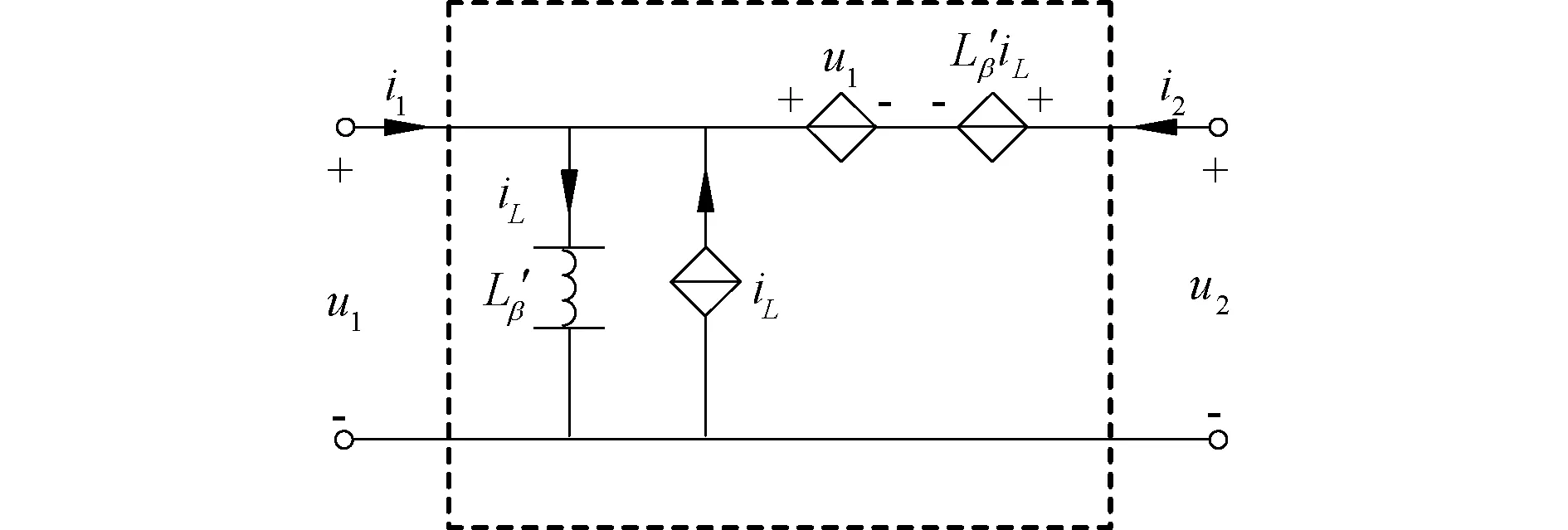
图5 含分数阶电感的Lβ-R变类器Fig.5 Lβ-R mutator with a fractional inductor
以图4为例进行分析,根据KCL和KVL定理,获得电路方程为
(10)
对式(10)整理可得:
(11)
式(11)与表1中给出的Lβ-R变类器的赋定关系相同,可知该电路可实现分数阶电感和电阻的相互变换。类似地,对图5中的电路进行分析,可得到相同的结果。
2.4 分数阶Mα,β-R变类器
图6给出了含分数阶元件实现的Mα,β-R变类器的电路结构,根据KCL和KVL定理,获得电路方程为
(12)
对式(12)进行整理可得:
(13)
由式(13)可知,该电路方程与表1中给出的Mα,β-R变类器的赋定关系相同,可实现分数阶忆阻与电阻之间的相互变换。

图6 含分数阶元件的Mα,β-R变类器Fig.6 Mα,β-R mutator with fractional elements
3 分数阶变类器的电路仿真研究
3.1 含分数阶电容的Lβ-R变类器仿真实例
根据图4给出的电路结构,采用Multisim电路仿真软件对所提出的分数阶Lβ-R变类器进行仿真验证。本例中采用的分数阶元件为一个0.2阶的分数阶电容,分别采用文献[24]和文献[25]中给出的近似方法对该分数阶元件在0.01~100 Hz内进行近似,得到的电路结构在图7和图8中给出,相应的电路参数在表3和表4中给出。
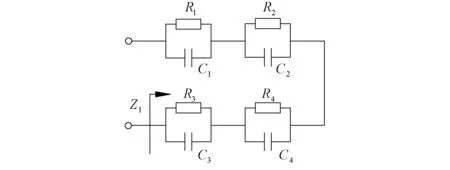
图7 文献[24]中给出的0.2阶电容的近似电路Fig.7 Approximation circuit of a 0.2 order fractional capacitor reported in [24]
Tab.3 Components parameters of the circuit depicted in Fig.7
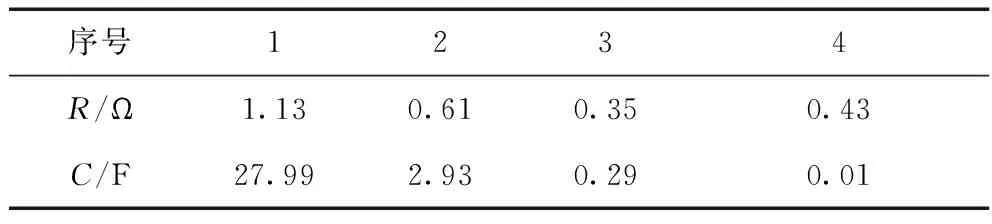
序号1234R/Ω1.130.610.350.43C/F27.992.930.290.01
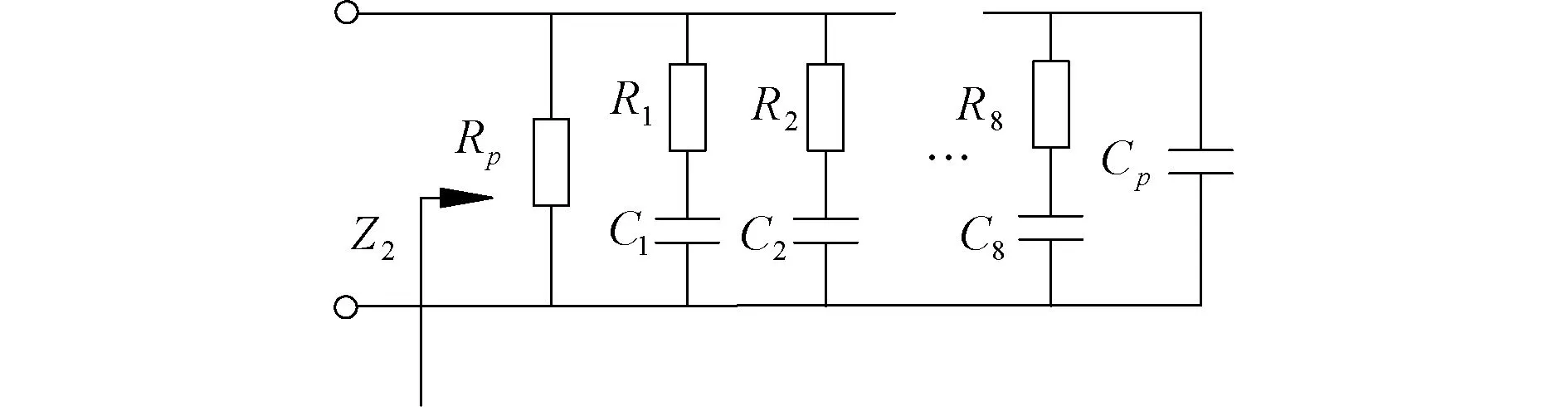
图8 采用文献[25]所述方法得到的0.2阶电容的近似电路Fig.8 Approximation circuit of a 0.2 order fractional capacitor obtained by using the method proposed in [25]
Tab.4 Components parameters of the circuit depicted in Fig.8
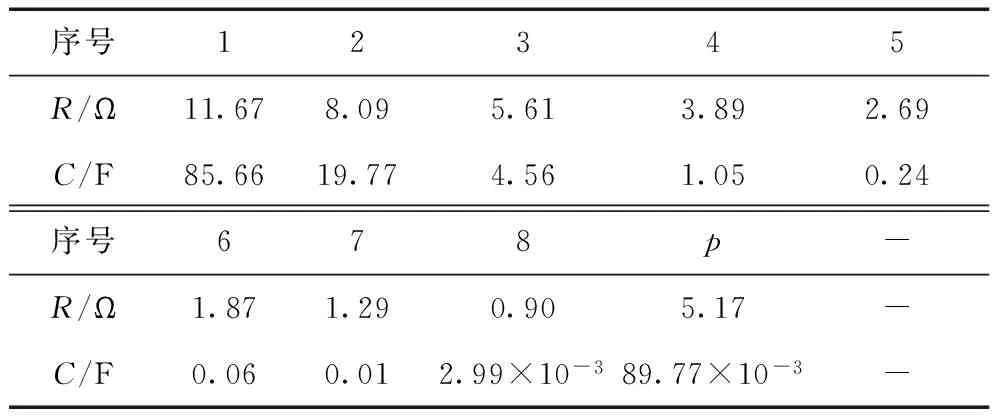
序号12345R/Ω11.678.095.613.892.69C/F85.6619.774.561.050.24序号678p-R/Ω1.871.290.905.17-C/F0.060.012.99×10-389.77×10-3-
使用Multisim对两个近似电路仿真得到的频率特性在图9中给出,同时在图中给出了理想分数阶电容的频率特性。由图9可知,两种近似电路都能在一定程度上对分数阶元件进行近似,其中图8所示电路比图7中的电路具有更好的拟合效果。在实际应用中,用户可以根据需要,参照文献[25]中的步骤,通过选取更多的元件来获得更好的近似效果。
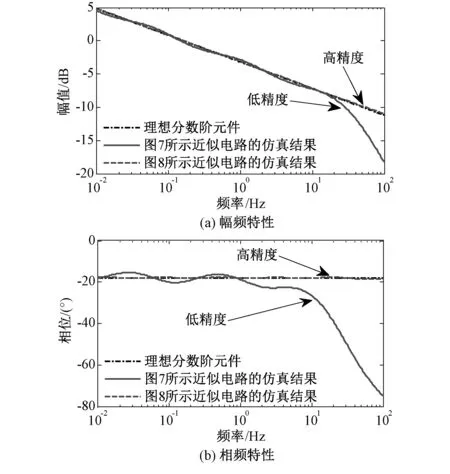
图9 0.2阶分数阶电容近似电路的频域特性Fig.9 Frequency responses of the approximation circuits of a 0.2 order fractional capacitor
根据分析可知,当图4所示的Lβ-R变类器右端端接一个100 mΩ的电阻时,从左端口看进去,该电路可等效为一个参数值为100 mH/s0.8的0.2阶分数阶电感元件。图10中给出使用Multisim仿真软件搭建的Lβ-R变类器电路,其中0.2阶分数阶电容采用图8所示的电路近似,并在图10中用蓝色方框标出。当采用图7所示的电路近似时,仅需替换蓝色方框中的电路即可。
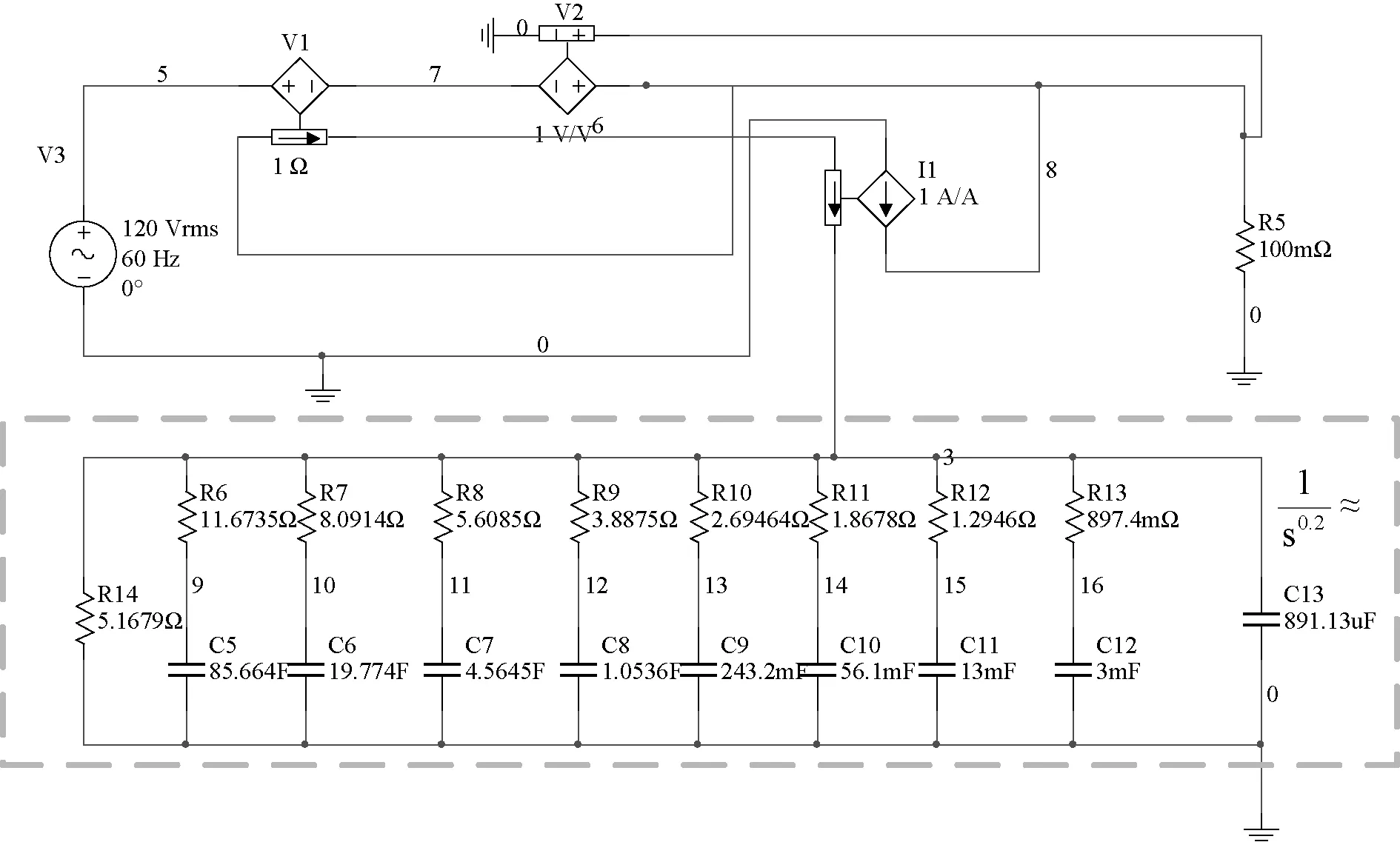
图10 含分数阶电容的Lβ-R变类器的Multisim仿真电路Fig.10 Simulation circuit of the Lβ-R mutator with a fractional capacitor
图11中给出了图10所示的仿真电路得到的频率特性,在图中同时给出了参数值为100 mH/s0.8阶次为0.2阶的理想分数阶电感元件的频域特性作为对比。由图11可知,所提出的分数阶Lβ-R变类器能够很好地实现分数阶电感元件和电阻元件间的相互变换。此外,当分数阶Lβ-R变类器中的分数阶元件采用高精度近似时,变换得到的元件也拥有更高的精度。
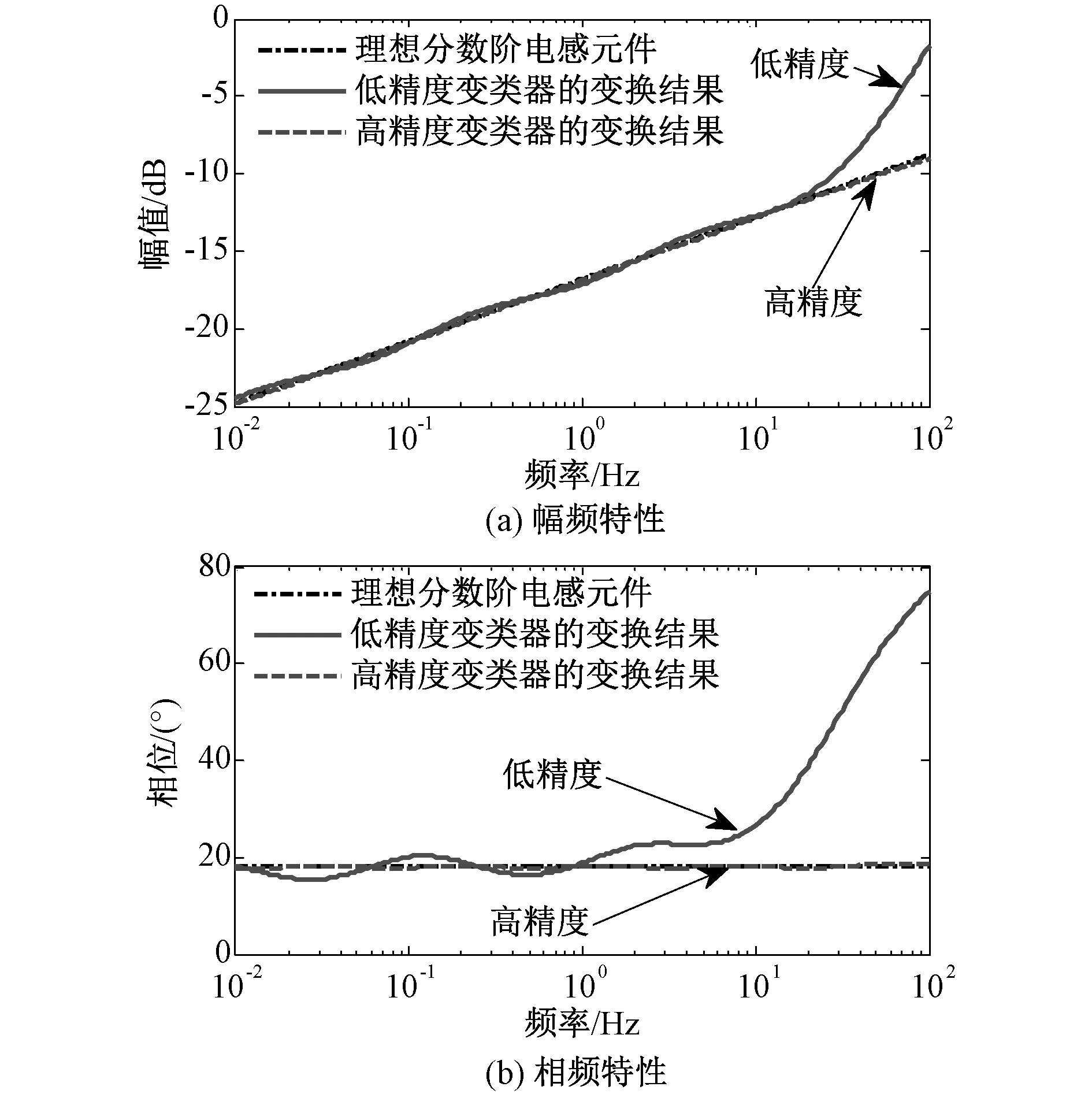
图11 变换得到的0.2阶分数阶电感的频域特性Fig.11 Frequency responses of the 0.2 order fractional inductor obtained by the Lβ-R mutator
3.2 分数阶Mα,β-R变类器仿真实例
根据图6给出的电路结构,采用Multisim电路仿真软件对所提出的分数阶Mα,β-R变类器进行仿真验证。本例中采用的0.2阶分数阶电容采用图8给出的电路进行近似,0.7阶分数阶电感也采用文献[25]中的方法进行近似,电路图和参数值分别在图12和表5中给出。
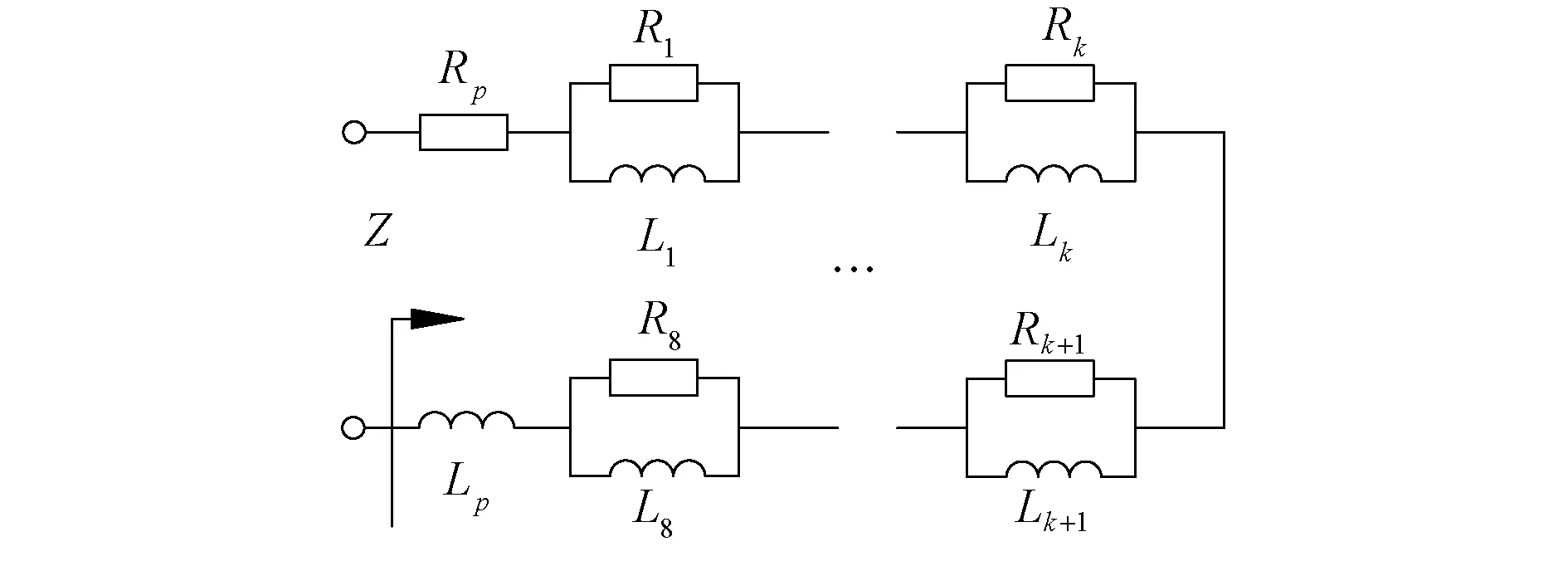
图12 采用文献[25]所述方法得到的0.7阶电感的近似电路Fig.12 Approximation circuit of a 0.7 order fractional inductor obtained by using the method proposed in [25]
根据分析可知,当图6所示的Mα,β-R变类器右端端接一个100 Ω的电阻时,从左端口看进去,该电路可等效为一个参数值为100 F/s0.5的0.5阶分数阶电容元件。图13中给出使用Multisim仿真软件搭建的Mα,β-R变类器电路,其中0.2阶分数阶电容采用图8所示的电路近似,并在图中用蓝色方框标出;0.7阶分数阶电感采用图12所示的电路近似,并在图中用绿色方框标出。
表5图12所示电路的元件参数
Tab.5 Components parameters of the circuit depicted in Fig.12

序号12345R/Ω3.11×10-39.02×10-326.18×10-376.00×10-30.22L/H3.111.971.250.790.50序号678p-R/Ω0.641.865.401.63×10-3-L/H0.320.200.130.22-
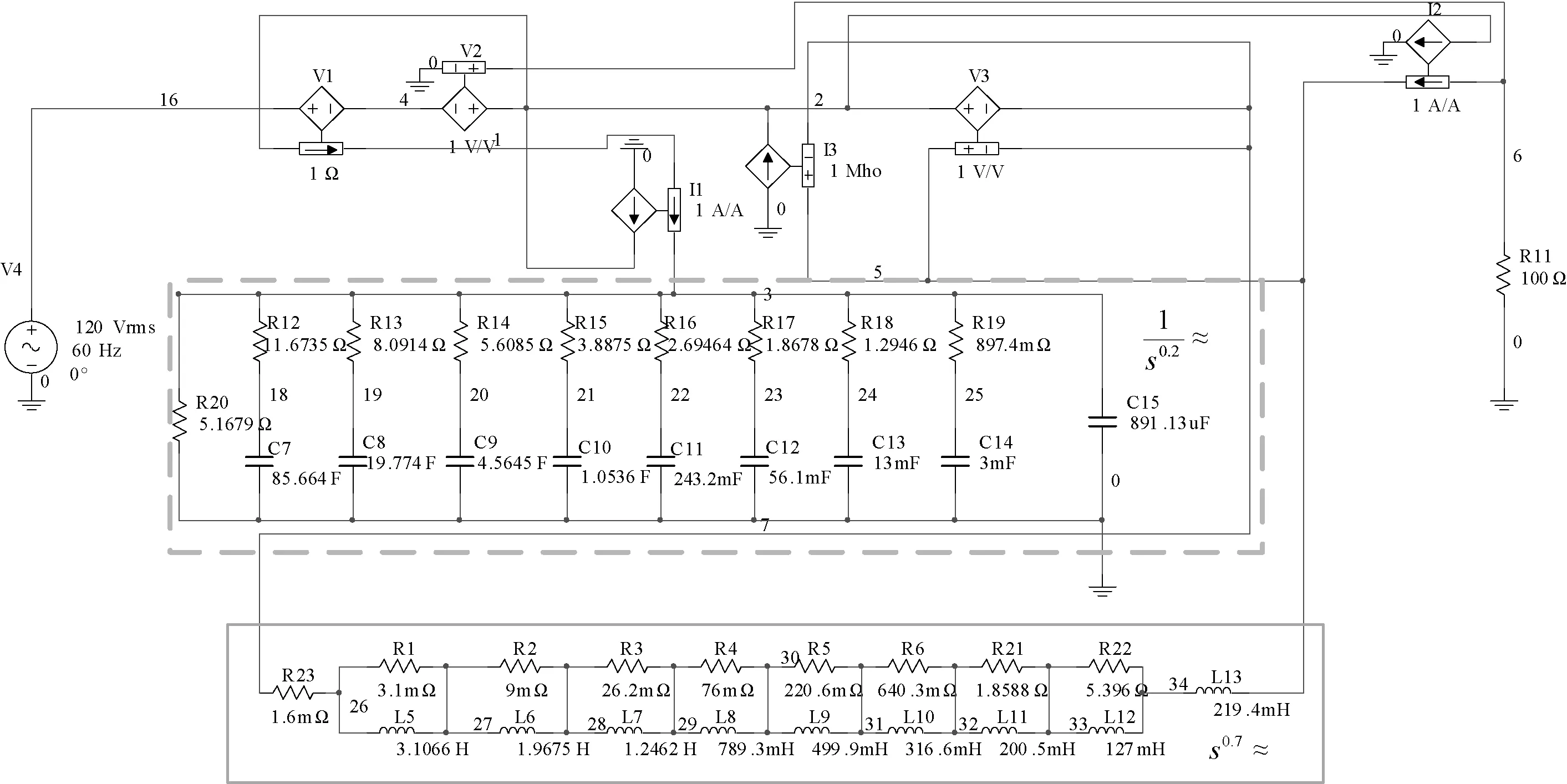
图13 分数阶Mα,β-R变类器的Multisim仿真电路Fig.13 Simulation circuit of the Mα,β-R mutator
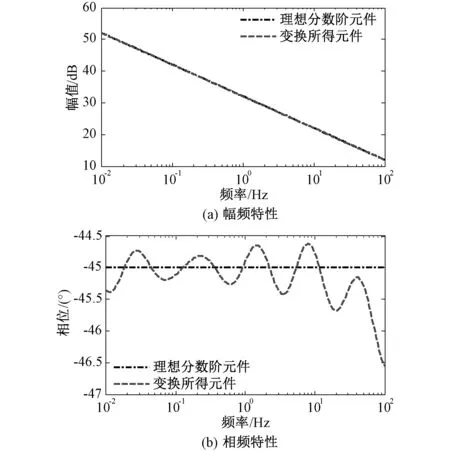
图14 变换得到的0.5阶分数阶电容的频域特性Fig.14 Frequency responses of the 0.5 order fractional capacitor obtained by the Mα,β-R mutator
图14中给出了图13所示的仿真电路得到的频率特性,在图中同时给出了参数值为100 F/s0.5阶次为0.5阶的理想分数阶电容元件的频域特性作为对比。由图14可知,所提出的分数阶Mα,β-R变类器能够很好地实现分数阶元件和电阻元件间的相互变换。
4 结 论
分数阶微积分理论是传统整数阶微积分的有力拓展。分数阶电路和系统的发展及其应用对分数阶元件的制造提出了新的要求。由于分数阶元件种类众多,制作繁杂,因此借助分数阶变类器,通过使用已有分数阶元件或易制造的分数阶元件实现新的或者难于制造的分数阶元件具有重要价值。
本文对传统的变类器进行有效拓展,给出了分数阶变类器的赋定关系和端口指数,实现了分数阶Cα-R、Lβ-R和Mα,β-R变类器,并通过Multisim电路仿真软件验证所提电路的正确性。未来的研究方向包括非线性分数阶电容、非线性分数阶电感、分数阶忆阻电路的实现与仿真研究。
[1] CHUA L O.Memristor—the missing circuit element[J].IEEE Transactions on Circuit Theory,1971,18(5):507-519.
[2] CHUA L O.Device modeling via nonlinear circuit elements[J].IEEE Transactions on Circuits and Systems,1980,27(11):1014-1044.
[3] CHUA L,SZETO E.Synthesis of higher order nonlinear circuit elements[J].IEEE Transactions on Circuits and Systems,1984,31(2):231-235.
[4] CHUA L O.Synthesis of new nonlinear network elements[J].Proceedings of the IEEE,1968,56(8):1325-1340.
[5] SOLIMAN A M.New L-R mutators and their models[J].International Journal of Electronics,1973,34(6):753-756.
[6] CHUA L O,SZETO E.Synthesis of higher order nonlinear circuit elements[J].IEEE Transactions on Circuits and Systems,1984, 31(2): 231-235.
[7] SWANY M N S.Mutators,generalized impedance converters and inverters,and their realization using generalized current conveyors[J].Circuits, Systems, and Signal Processing,2011, 30(1):209-232.
[8] YU D,LIANG Y,IU H C,et al.A universal mutator for transformations among memristor,memcapacitor,and meminductor[J]. IEEE Transactions on Circuits and Systems II:Express Briefs,2014,61(10):758-762.
[9] PODLUBNY I.Fractional differential equations: an introduction to fractional derivatives,fractional differential equations,to methods of their solution and some of their applications[M].Academic Press,1998.
[10] 梁贵书,王雁超.考虑频变参数的油浸式变压器绕组分数阶传输线模型[J].电工技术学报,2016,31(17):178-186.
[11] 梁贵书,高世强.油浸式变压器绕组分数阶传输线模型参数辨识的研究[J].华北电力大学学报(自然科学版),2016,43(5):1-7.
[12] 刘欣,崔翔,梁贵书,等.基于分数阶微分理论的宽频建模方法[J].电工技术学报,2013,28(4):20-27.
[13] WU C,SI G,ZHANG Y, et al.The fractional-order state-space averaging modeling of the Buck-Boost DC/DC converter in discontinuous conduction mode and the performance analysis[J].Nonlinear Dynamics, 2015,79(1):689-703.
[14] BERTRAND N,SABATIER J,BRIAT O,et al.Fractional non-linear modelling of ultracapacitors[J].Communications in Nonlinear Science and Numerical Simulation,2010,15(5):1327-1337.
[15] NAKAGAWA M.Basic characteristics of a fractance device[J].IEICE Transactions on Fundamentals of Electronics,Communications and Computer Sciences,1992,75(12):1814-1819.
[16] SOLTAN A,RADWAN A G,SOLMAN A M.Fractional-order mutual inductance:analysis and design[J].International Journal of Circuit Theory and Applications,2015,44(1):85-97.
[17] SÜSSE R,DOMHARDT A,REINHARD M.Calculation of electrical circuits with fractional characteristics of construction elements[J].Forschung im Ingenieurwesen,2005,69(4):230-235.
[18] BISWAS K,THOMAS L,CHOWDHURY S,et al.Impedance behaviour of a microporous PMMA-film coated constant phase element based chemical sensor[J].International Journal of Smart Sensing and Intelligent Systems,2008,1(4):922-939.
[19] HABA T C,ABLART G,CAMPS T,et al.Influence of the electrical parameters on the input impedance of a fractal structure realised on silicon[J].Chaos,Solitons and Fractals,2005,24(2):479-490.
[20] SAID L A,ISMAIL S M,RADWAN A G,et al.On the optimization of fractional order low-pass filters[J].Circuits,Systems,and Signal Processing,2016,35(6):2017-2039.
[21] 王振滨,曹广益,朱新坚.分数阶线性定常系统的稳定性及其判据[J].控制理论与应用,2004,21(6):922-926.
[22] 马龙,梁贵书,董华英.含分数阶电抗元件网络的灵敏度分析[J].华北电力大学学报(自然科学版),2013,40(3):6-10.
[23] COOPMANS C,PETRAS I,CHEN Y Q.Analogue fractional-order generalized memristive devices[C].ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference,San Diego,2009.
[24] AHMAD W M,SPROTT J C.Chaos in fractional-order autonomous nonlinear systems[J].Chaos,Solitons and Fractals,2003,16(2):339-351.
[25] VALSA J,DVORAK P,FRIEDL M.Network Model of the CPE[J].Radioengineering,2011,20(3):619-626.
Study on Fractional Two-port Mutator and Its Circuit Simulation
LIANG Guishu,MA Long,SHAN Dongqing
(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)
Mutators are generalized in this paper on the basis of fractional calculus. A unified model is established, then both of constitutive relations and transfer functions of 12 types of mutators are presented in detail. And theCα-R,Lβ-RandMα,β-Rmutators in type I are formed. Finally, the results of simulation with the aid of Multisim software verify the validation of the above mutators.
fractional calculus; mutator; two-port networks; Multisim circuit simulation
2017-03-03.
国家自然科学基金资助项目(51177048).
10.3969/j.ISSN.1007-2691.2017.06.01
TM134
A
1007-2691(2017)06-0001-07
梁贵书(1961-),男,教授,博士生导师,研究方向为分数阶微积分理论,电网络理论及其应用,电力系统电磁兼容和电力信息分析与处理等;马 龙(1988-),男,博士研究生,研究方向为分数阶微积分理论,电网络理论及其在电力系统中的应用;单栋清(1990-),男,硕士研究生,研究方向为分数阶微积分理论,电网络理论及其在电力系统中的应用。
