小学生对数学文化呈现方式的接受度研究

付天贵，宋乃庆



小学生对数学文化呈现方式的接受度研究

付天贵1，2，宋乃庆2

（1．西南大学 数学与统计学院，重庆 400715；2．重庆文理学院 数学与财经学院，重庆 402160）

数学文化整合于数学课程是基础教育数学课程改革的要求．数学文化在小学数学课程里通常以连环画的形式、情境图的形式和纯文本形式呈现．从国内小学数学教材中选择内容相同，但呈现形式不同的内容让学生进行阅读，然后进行问卷调查、自我陈述和访谈，研究小学生对小学数学文化呈现方式的接受度，其结论是：小学生对连环画呈现方式的接受度高于情境图呈现方式和纯文本呈现方式；年级对数学文化编写方式的接受度呈现相同趋势．兴趣性、形象性、可读性和连贯性是影响小学生数学文化接受度的主要因素，在把数学文化融于小学数学教材时，要考虑不同学段，灵活运用不同的呈现方式．

小学生；数学文化；呈现方式；接受度

1 问题提出

随着数学课程改革的发展，人们认识到必须把数学文化融合于课程，形成科学与人文相融合的课程观念．把数学文化融合于数学课程，加强数学文化内容的教学实践，提高学生的数学素养是数学课程改革的潮流和趋势．中国义务教育数学课程标准提出了“人人都能获得良好的数学教育，不同的人在数学上获得不同的发展”的数学课程理念，标准指出：“数学文化作为教材的组成部分，应渗透在整套教材中．为此，教材可以适时地介绍有关背景知识，包括数学在自然与社会中的应用，以及数学发展史的有关材料，帮助学生了解在人类文明发展中数学的作用，激发学习数学的兴趣，感受数学家治学的严谨，欣赏数学的优美．”[1]教材承担着科学文化的积累、继承和发展的任务，承担着科学文化传播的任务[2]．在新的课程观指导下，正在实施的中国小学数学新教材纷纷编入数学文化内容．

数学文化融合于数学课程意味着传统数学课程内容和形式的改变，是数学课程观的变革与发展，是数学自身文化的发展．美国数学家R·L·怀尔德认为数学是一个由其内在力量与外在力量共同作用而处于不断发展和变化之中的文化系统[3]．怀尔德立足于数学史，从数学自身、文化环境、数学与文化共同作用3个方面描述了数学发展的多元互动机制，总结了数学发展的23条规律．怀尔德认为数学是一种文化体系，并认为数学文化是由文化传统和数学本身所组[4]．数学文化的内涵国内外有多种解释，数学文化是数学知识、数学精神、数学思想、思维方式等文明的总和[5]．数学文化包括了数学史、数学家的故事、数学的应用等物化内容，有学术形态、课程形态和教育形态3种形态[6]．小学数学新教材多以“你知道吗”、“数学广角”、“数学园地”、“数学文化”、“数学游戏”、“数学万花筒”、“数学应用”、“数学阅读”、“数学故事”等栏目编写数学家的故事、数学史、数学的应用等内容，此处的数学文化特指小学数学教材该部分内容．

通过研读中国目前使用的小学数学教材[7-12]，发现在小学阶段数学文化呈现方式有3种：一是以情境图形式呈现，二是以纯文字叙述形式呈现，三是以连环画的形式呈现．学生对数学文化融合与课程是否接受？对不同呈现方式接受情况是怎样的？不同年级接受情况是否一致？农村和城市学校学生接受情况是否相同？这些问题是数学课程发展所必须回答的，值得深入研究．

2 研究过程

阅读是数学文化学习中必不可少的阶段．韦德、斯科诺等以大学生为研究对象，采用出声思维的办法证实了知识经验对阅读兴趣的影响，发现阅读时缺乏足够的知识背景，就会抱怨读不明白，认为文本是无趣的[13]．研究基于这样的假定：通过阅读学生不但可以获得大量知识，同时依据对相同数学文化的不同呈现，学生能从内容的兴趣性、形象性、可读性和连贯性等方面认识数学文化的内容及其所蕴含的思想，进而对呈现方式作出选择．通过研读小学数学教材发现：聪明的高斯、祖冲之与圆周率、哥德巴赫猜想这3个内容都被整合到现行小学数学教材，只是出现在不同的年级，同时有的以纯文字形式呈现，有的以主题图或连环画形式呈现．研究首先邀请高校专家、教研员和一线教师对同一内容编写另外两种形式，然后组织学生对同一内容的不同形式进行阅读，进行问卷调查，最后是访谈．

3 研究方法

3.1 调查法

3.1.1 调查工具

接受度指学生对小学数学文化的正面态度或行为意向．为研究学生对不同呈现方式的接受度，利用自编的“小学数学文化实施问卷”进行了调查．问卷采用5级量表制，首先呈现相同内容的不同编写方式，然后出示题项，并附有一开放题要求被调查学生简单写一写原因．

3.1.2 调查对象

调查对象来自重庆市某区县四、五、六年级，其中四年级学生240人，五年级学生232人，六年级学生220人，共计692人．抽样时考虑了样本的代表性和分布．

3.1.3 数据分析

采用定量与定性相结合的原则对问卷进行综合分析．首先对问卷进行定量统计分析，然后采用等距原则进行等级评定，五级评分标准是：A等级(1.00—1.80)为反对，B等级(1.8—2.6)为较反对，C等级(2.60—3.40)为中立，D等级(3.40—4.20)为比较赞同，E等级(4.20—5.00)为赞同．

3.2 访谈法

问卷调查适合于宏观层面大面积地进行统计调查，能对事物的一些比较表面的、可以量化的部分进行测量，但不能获得细节的内容．学生在对数学文化呈现方式进行判断时，必须通过阅读理解课程所表达的内容．在学生完成问卷调查后，采用访谈法，通过询问有关问题以了解学生作出判断的依据．访谈结果是一种实证事例，实证事例对于结论不是完全的、必然的证实，也不是逻辑的证明，只是一定程度的支持．访谈提纲由3个问题组成：你读懂有关内容了吗？你最喜欢哪一种编写方式？为什么喜欢这种编写方式？访谈过程中，教师根据学生的回答情况，适时追问．

4 结果与讨论

4.1 问卷调查结果

4.1.1 小学生数学文化呈现方式接受度

呈现方式的平均得分及等级评定，反映出学生对新课程小学数学文化的接受度．小学生对数学文化编写方式的接受度见表1．

表1 呈现方式的接受度

3种呈现方式平均得分有高到低的顺序是连环画、情境图、纯文本．连环画呈现方式的平均分为4.042 6，等级评定为D，情境图呈现方式和纯文本呈现方式等级评定为C．

4.1.2 年级对呈现方式接受度的影响

为弄清楚不同年级学生对不同编写方式的接受情况，统计了不同年级学生呈现方式的评价得分，结果见表2．

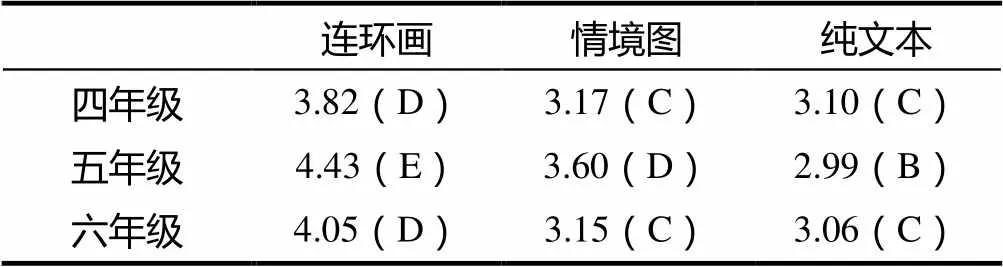
表2 不同年级呈现方式的接受度

不同年级学生对数学文化编写方式的接受度呈现相同趋势，连环画呈现形式接受度高于情境图呈现形式接受度，且都高于纯文形式接受度，这与总体情况相同．但也出现不同特点，五年级学生对连环画呈现形式接受程度等级评定达到E，而纯文本形式等级评定为B．

4.1.3 学校性对呈现方式接受度的影响

调查对象包括了乡村小学、乡镇小学和城市小学的学生，表3是不同性质学校对数学文化呈现方式的接受情况统计表．

表3 不同类别学校呈现方式的接受度

不同性质学校对数学文化编写方式的接受度与总的情况相同，对连环画呈现形式接受度高于另外两种形式．从表2和表3可以看出，不同类别学校、年级对学生数学文化接受度几乎一致．

4.1.4 影响接受度的主要因素

研究过程中，从内容的兴趣性、形象性、可读性和连贯性等几个方面对影响小学生数学文化呈现方式接受的原因进行了调查，结果如表4所示．

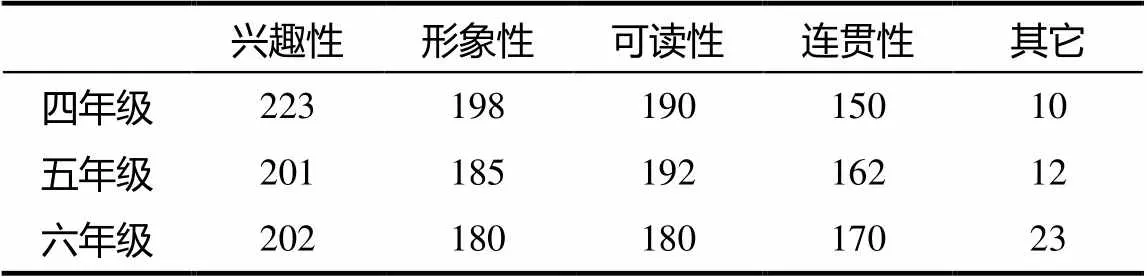
表4 影响接受度的主要因素

统计结果表明，数学文化的兴趣性、形象性、可读性和连贯性都是影响小学生数学文化呈现方式接受的原因．统计过程中发现，在回答做出呈现方式选择因素时，虽然有学生选择其它，但都没有具体说明其它是什么因素．

4.2 访谈结果

在学生完成问卷后，从每个班抽取5名进行访谈，每个年级都访谈了25人．在回答第1问“你读懂有关内容了吗？”学生几乎都回答能读懂有关内容．对第2问“你最喜欢哪一种编写方式？”的统计如表5所示．

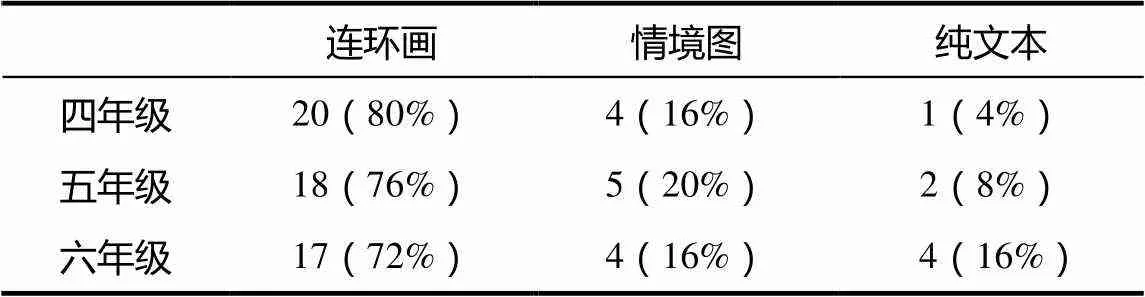
表5 学生最喜欢的编写方式

统计结果表明，73%左右的调查学生都选择连环画呈现方式．在回答“你为什么喜欢连环画这种编写方式？”这一问题时，学生的回答主要集中于有趣、形象直观、更容易读懂、故事比较完整；访谈时，在回答了最喜欢的编写方式是情境图后，回答“你为什么喜欢这种编写方式？”这一问题时，学生的回答主要是简洁，能读懂；在回答了最喜欢的编写方式是纯文本后，回答“你为什么喜欢这种编写方式？”这一问题时，学生的回答主要是能读懂、节约纸张，有一个学生回答非常特别，他说：我喜欢阅读，所以纯文本的方法较好．访谈结果进一步证明有趣、形象直观、容易读懂是影响接受度的主要因素．

从访谈情况看，能读懂内容是学生选择呈现方式的关键因素．学生读不懂内容，根本不会对内容产生兴趣，只有在读懂课程内容的情况下，学生才会结合自己的特点考虑外在的形式，如可读性、形象性、简洁性和连贯性等特性，当然这些特性也影响着学生是否理解了内容．从访谈情况看，有时学生并未真正读懂情境图，例如聪明的高斯的情境图选自人教社小学数学教材[14]，其编写方式如下：

设计该内容的目的是希望学生在阅读后认真思考：高斯到底是怎么计算的呢？同时通过自己动手计算、查阅书籍、上网查询，或是询问老师、同伴、家长获得问题解决．访谈过程中在回答第3个问题“你为什么喜欢这种呈现方式？”时，有学生是这样理解该情境图：图片里有老师在给同学们讲课，这要求在学习该内容时教师要进行讲解，这样也就更能理解．情境图只是借助教师人物形象提出“1+2+3+…+99+100的和是多少？”这一问题让学生进行思考，并不是要求教师讲解，由此可以看出学生并没有真正理解情境图．数学文化整合于课程是弹性设计，其主要目的不是知识讲解和传授，而在于学生数学阅读习惯的培养，兴趣的激发，思维的拓展．

5 结论与思考

就小学数学文化的呈现方式而言，小学生连环画呈现方式的接受度等级评定为D，情境图呈现方式和纯文本呈现方式等级评定为C，小学生连环画呈现方式的接受度高于另外形式．分析其原因主要有以下几个方面：第一，用连环画形式呈现可以把抽象的数学内容直观表现，易于学生理解，符合小学生的认知特点和心理需求，正如中国科学院刘应明院士所言：连环画形式呈现的科普读物，相信不少孩子会感到“数学好玩”[15]；第二，以故事形式呈现数学文化内容，相对于另外两种呈现方式而言，人物的对话使得数学文化更具动态性，学生可以借助图画进行想象和联想；第三，连环画形式呈现时，通常用几幅画陈述同一件事，使故事具有完整性．一个五年级学生在回答你最喜欢哪一种呈现方式的原因时写到：“读了陈景润与哥德巴赫猜想的故事，想想陈景润用了十多年的时间去证明（哥德巴赫猜想），纸都用了6麻袋，使我认识到学好数学必须努力．”

学生对连环画呈现方式接受度高于情境图和纯文本的接受度．就年级和不同性质学校对小学数学文化的呈现方式来说，可以得到相同的结论，连环画的呈现方式接受度高于情境图接受度，而情境图的接受度高于纯文本接受度．原以为低年级对连环画呈现方式接受度要高于高年级，但调查的结果四年级对连环画呈现方式接受度低于五、六年级，该结果出乎意料．分析原因，主要是学生刚升上四年级（调查是在第一学期开学不久进行调查的），识字还不多，对内容的理解相对较弱，容易出现偏差，特别是对以纯文本形式呈现的内容．

兴趣性、形象性、可读性和连贯性是影响学生接受数学文化的主要因素，阅读时能读懂数学文化的内容是学生选择呈现方式的关键因素．在选择数学文化内容时，要考虑学生的年龄特征，选择学生能读懂、可接受的内容，在把数学文化整合于课程时要综合考虑形象性、可读性和连贯性．就小学数学教材的编写而言，考虑到小学生对数学文化内容的呈现方式的接受度，宜采用连环画呈现数学文化．但由于中国对教材实现严格审查制度，教材开本和页面数量都有严格规定，以连环画形式呈现小学数学内容，虽然直观形象和便于理解，同时故事也相对完整，但是一个故事通常是1~2页，受版面因素影响，这会限制把更多的数学文化融于数学教材．这启示课程专家在把数学文化融于小学数学教材时，要灵活运用不同的呈现方式，小学低段可以连环画为主，另外两种方式为辅，在高段，特别是5、6年级小学数学教材，由于学生具备一定的阅读能力，可纯文本为主，另外其它形式为辅．

总之，加强对学生进行数学文化方面的教育活动，是课程改革的趋势，其作用是拓展视野、激发兴趣，让学生接受文化熏陶，培养和提高学生数学素养．在把数学文化融于教材时，要根据内容的需要，表述简明扼要，同时编排形式要新颖灵活，不拘一格．

[1] 中华人民共和国教育部．全日制义务教育数学课程标准[M]．北京：北京师范大学出版社，2011：63．

[2] 范印哲．大学教材设计模式的理论框架探析[J]．中国大学教学，2003（2）：33-34．

[3] WILDER R L. The evolution of mathematical concepts: an elementary study [M]. New York: Wiley, 1968: 3.

[4] 张俊青，郭燕霞．数学：开放的文化系统——怀尔德论数学发展的动力和规律[J]．长治学院学报，2006，32（2）：23-25．

[5] 宋乃庆．小学数学文化丛书[M]．重庆：西南师范大学出版社，2014：1．

[6] 张广祥，张奠宙．代数教学中的模式直观[J]．数学教育学报，2006，15（1）：1-4．

[7] 卢江．义务教育教科书·小学数学（一上）[M]．北京：人民教育出版社，2014：60．

[8] 刘坚，孔企平，张丹．义务教育教科书·小学数学（四上）[M]．北京：北京师范大学出版社，2014：13．

[9] 宋乃庆．义务教育教科书·小学数学（一上）[M]．重庆：西南师范大学出版社，2014：55．

[10] 孙丽谷，王林．义务教育教科书·小学数学（一下）[M]．南京：江苏教育出版社，2012：39．

[11] 展涛．义务教育教科书·小学数学（三下）[M]．青岛：青岛出版社，2014：64．

[12] 赵杏梅．义务教育教科书·小学数学（五上）[M]．石家庄：河北教育出版社，2014：95．

[13]  WADE S F, SCHRAW G, BUCTON W M, et al. Using think-alouds to examine reader-test interest [J]. Reading Res. Quart,1999 (34): 194-216.

[14] 卢江，杨刚．义务教育教科书·小学数学（四下）[M]．北京：人民教育出版社，2010：32．

[15] 刘应明．惠及子孙，功德无量的大胆尝试——评宋乃庆主编《小学数学文化丛书》[J]．数学教育学报，2015，24（4）：3．

附录：卷调查表（部分）

数学文化问卷调查表（部分）

亲爱的同学：

你好！非常感谢您参加本次问卷调查．由于研究的需要，需要对小学数学课程实施的情况进行调查．本问卷只用于研究，不记名，也不涉及个人和学校的具体评价，请不必有任何顾虑．答案没有正确与错误之分，请您根据实际情况进行回答．谢谢你的合作！

西南大学基础教育课程研究中心

一、你的个人信息（请在符合您的情况的选项前面画勾）

1．你的年龄：A. 9岁以下 B. 9~10岁 C. 10~11岁 D. 11岁以上

2．所在年级：A. 1年级 B. 2年级 C. 3年级 D. 4年级 E. 5年级 F. 6年级

3．学校性质：A. 乡村学校 B. 乡、镇中心学校 C. 城市小学

二、下面每一内容有3种编写方式，请首先阅读有关内容，然后根据实际情况回答．

（一）下面方式一，方式二，方式三都是小学教材中叙述的高斯的故事．

编写方式一：

高斯是德国数学家，是近代数学奠基者之一,他和牛顿、阿基米德被誉为有史以来的三大数学家，有“数学王子”之称．高斯学习非常勤奋，11岁时发现了二项式定理，17岁时发明了二次互反律，18岁时发明了用圆规和直尺作正17边形的方法，解决了两千多年来悬而未决的难题．21岁大学毕业，22岁时获博士学位．

高斯出生于德国的一个贫苦家庭．7岁那年，高斯第一次上学了，在全世界广为流传的一则故事说，高斯最出名的故事就是他十岁时，小学老师出了一道算术难题：“计算1＋2＋3…＋100＝?”．这可难为初学算术的学生，但是高斯却在几秒后将答案解了出来．小朋友，你知道高斯是怎么算的吗？试一试．

编写方式二：

编写方式三：

阅读完后，请在1、2、3题中任选一题做答

1. 在阅读时我喜欢方式一．（ ）

A. 反对 B. 稍微反对 C. 中立 D. 稍微赞同 E. 赞同

2. 在阅读时我喜欢方式二．（ ）

A. 反对 B. 稍微反对 C. 中立 D. 稍微赞同 E. 赞同

3. 在阅读时我喜欢方式三．（ ）

A. 反对 B. 稍微反对 C. 中立 D. 稍微赞同 E. 赞同

4.（可以多选）请在你认为的选项上打√．作出上面的选择，是阅读时候我觉得内容具有（ ）

A. 兴趣性 B. 形象性 C. 可读性 D. 连贯性 E. 其它 选择其它，请具体说说在什么原因：

5. 按最喜欢、第二喜欢、第三喜欢的次序对编写方式排序，你的排序是：

[责任编校：周学智]

Primary School Students’ Acceptance of Mathematics Culture Presentation Modes

FU Tian-gui1, 2, SONG Nai-qing2

(1. School of Mathematics and Statistics, Southwest University, Chongqing 400715, China; 2. School of Mathematics and Finance, Chongqing University of Arts And Science, Chongqing 402160, China)

The integration of mathematics culture into mathematics curriculum was a basic requirement for mathematics curriculum reform in China. Mathematics culture was generally represented as serial comics, situational pictures, and plain text. This study investigated the acceptance of mathematics culture at primary school level in China. It was found that for Chinese primary school students, they accepted mathematics culture as presented in the style of serial comics most. No big difference was found between students from different grades, and urban and rural students. Interest, visualization, readability and coherence were the main factors that influence the acceptance of mathematics of elementary school students. For textbook writers, they should consider to present mathematics culture in more different ways to increase students’ acceptance.

primary school students; mathematics culture; presentation; acceptability

G622

A

1004–9894（2017）06–0036–04

付天贵，宋乃庆．小学生对数学文化呈现方式的接受度研究[J]．数学教育学报，2017，26（6）：36-39．

2017–06–11

2016年度教育部人文社会科学研究项目——数学文化对小学生核心素养的影响研究（16YJAZH009）；2016年度重庆市教委人文社会科学研究项目——数学文化对小学生数学兴趣的影响研究（16SKGH161）

付天贵（1969—），男，重庆人，副教授，西南大学博士生，主要从事数学课程与教育研究．宋乃庆为本文通讯作者．