数学教育中学习进阶的研究进展及启示

吴颖康，邓少博，杨 洁



数学教育中学习进阶的研究进展及启示

吴颖康，邓少博，杨 洁

（华东师范大学 数学系，上海 200241）

学习进阶的概念源于美国科学教育领域．从国际视野来看，数学教育中的学习进阶研究正处于起步阶段，可基本分为两大类．第一类是关于学习进阶的基础性研究，即以实证方法建立描述学生关于某数学学习主题认知纵深发展的学习进阶，第二类是学习进阶在数学课程、教学和评价等领域的应用性研究．在简述学习进阶涵义和特征之后，以因数概念为例介绍学习进阶的建立过程和方法，呈现并分析学习进阶在数学评价、课程和教学等领域的应用性研究示例，最后指出要充分认识学习进阶在数学教育中的理论价值和实践意义，要以学习进阶的基础性研究为根基，积极推广其在数学课程、教学和评价等领域中的应用性研究．

学习进阶；数学教育；研究；启示

学习进阶的概念源于美国科学教育领域．2005年美国国家研究理事会（National Research Council，简称NRC）在关于K-12年级科学成就测试的工作报告中正式提出了学习进阶的概念，以克服美国科学课程内容分散且缺少联系的弊端，促使课程和评估的一体化．近年来，学习进阶逐渐进入数学等其它学科的教育教学领域．从国际视野来看，数学教育中的学习进阶研究正处于起步阶段，可基本分为两大类．第一类是关于学习进阶的基础性研究，即以实证方法建立描述学生关于某数学学习主题认知纵深发展的学习进阶，第二类是学习进阶在在数学课程、教学和评价等领域的应用性研究．这里首先简述学习进阶的涵义和特征，其次以因数概念为例介绍学习进阶的建立过程和方法，接着呈现学习进阶在数学评价、课程和教学等研究领域中的应用性研究示例，最后在分析中国学习进阶研究现状的基础上提出若干建议，以期对推动中国学习进阶的研究有所启示和裨益．

1 学习进阶的涵义和特征

学习进阶尚未有统一定义，归结起来可分为如下4类．（1）过程论：Songer等认为“学习进阶是学生对学习主题思考、推理和探究的过程”[1]；Merrit等将学习进阶定义为“描述学生对某一主题由浅入深、逐渐复杂的概念理解过程”[2]．（2）假设论：Salinas提出学习进阶是“以实证为基础的、可检验的假说，它阐释了在一段时间内经过适当的教学，学生对科学核心概念、科学解释以及科学实践的理解和运用是如何逐渐发展、逐步深入的”[3]；Duncan 等认为“学习进阶其实是一种假设，是一系列以实证为基础、可检测的假设，是对学生在适当的教学条件下，随着时间的推移，对核心科学概念、科学解释以及相关的科学实践的理解和应用能力逐渐变得复杂的一种假设——验证过程”[4]．（3）方法论：Smith等将学习进阶描述为“在学生学习过程中，以内容为载体，相互联结、不断深入复杂、循序渐进的一种推理探究方法”[5]．（4）序列论：Roseman等认为学习进阶是一条由小学延续到高中的、有逻辑的、符合学生认知发展规律的“概念序列”[6]；Alonzo与Steedle认为学习进阶是“学生对某一概念理解的有序描述”[7]．

目前被广泛接受的是由美国国家研究理事会（NRC）提出的定义[8]，融合了过程论与假设论，即在一个较大时间跨度内，学生对某一学习主题的思考和认识不断丰富、精致和深入的一种过程，旨在揭示学生在学习和探索某一主题时，对该主题的思考、理解与实践活动在相当长的一段时间内是如何从简单到复杂、从低水平到高水平、从新手到专家逐步发展的，是在大量实证研究的基础上形成的一种假定性描述，可以通过实践加以检验．

由上述定义可归纳出学习进阶的3特征：第一，它是描述学生关于某一学习主题的理解和认识如何逐步发展的、以实证为基础的、可检验的假说；第二，它具有层次性和阶段性；第三，它有助于整合零碎分散的知识，形成有系统的知识序列或概念网络．

数学教育研究领域中有一个类似的概念“学习轨迹”（Learning Trajectory），同样刻画了学生关于某个学习主题的认知由简单到复杂的发展过程，具备学习进阶的上述3个特征，只是更为具体详细，涉及对发展学生认知的相关教学活动的描述[9]．鉴于学习进阶和学习轨迹在本质上的一致性[10]，这里对学习进阶与学习轨迹不做区分．

2 学习进阶的基础性研究：以因数概念学习进阶的建立为例

学习进阶包含如表1所示的5个基本要素[8，11]．学习进阶的建立过程实际上就是通过评价手段明确前4个要素的过程．目前文献中并没有一套通用的建立学习进阶的方法，但总结起来不外乎以下3个步骤：资料的收集和整理、假想的学习进阶的提出、学习进阶的检验和修正．下面以因数为例[12]对建立学习进阶的这3个步骤加以解释．学习进阶的5个要素如表1所示．

表1 学习进阶的5个要素

首先，研究者对数学课程纲要和教科书中有关因数与倍数的内容进行梳理，明确该内容的学习目标，并发现学生在学习因数与倍数前必须先了解“整除”以及“几的几倍”的概念，因而将因数与倍数的学习进阶分解为整除、因数、倍数3个维度，即确定了3个发展变量．之后对整除、因数与倍数的相关文献进行梳理，尤其关注学生的错误类型及其之间的联系．

其次，在上述文献分析的基础上，兼顾现阶段学生的实际学习表现，研究者设计了针对因数与倍数的访谈提纲，对某小学二~六年级共14位学生进行了访谈，以了解不同年级学生在因数与倍数等相关概念上的表现，为建立假想的学习进阶提供依据．这里将以因数的学习进阶为例进行展开．访谈结果发现，学生学习因数时遵循“因数—公因数—最大公因数”的认知发展顺序，而且该顺序也符合因数内容的逻辑发展顺序；此外，学生必须先掌握乘除法中各成分元素彼此之间的关系，之后才能理解因数的概念．在此基础上，研究者提出了如表2所示的因数的假想的学习进阶．

依据假想的学习进阶，研究者开发了因数学习进阶的测试卷，以评价不同能力学生在因数内容上的表现与假想的学习进阶中的水平刻画是否相符．共有来自5所小学三~六年级的454位学生参加了测试．根据测试结果，研究者对假想的学习进阶进行了修正．例如，研究者原来认为学生应在掌握因数概念后才能掌握因、倍数互逆的概念，但测试结果却表明一部分初步掌握因数概念的学生就已经可以通过因数与倍数的关系解决简单的因、倍数互逆问题，因此研究者将因、倍数互逆的层级位置进行了调整，在层级二中新增“能够意会简单的因、倍数互逆关系”的叙述．修正后的因数的学习进阶如表2所示，共分6个层级，每个层级均给出了能力表现的具体描述，除最高层级外的每个层级还给出了尚未习得的知识与错误类型．

3 学习进阶在数学教育研究领域中的应用性研究

如果说学习进阶的基础性研究回答了是什么的问题，那么学习进阶的应用性研究则回答了有什么用的问题．这里将结合具体实例描述和讨论学习进阶在评价、课程和教学等领域中的应用．

3.1 学习进阶与评价

学习进阶的建立依赖于评价，因此学习进阶与评价之间有着天然的联系．以往的学习评价，无论是终结性评价还是形成性评价，都关注于描述学生在某个学习领域内的学习表现，并没有关注学生就某个核心概念或过程的理解的纵向发展过程，基于学习进阶的评价能弥补这一缺陷．通过实证手段建立的学习进阶描述了学生关于某个学习主题的发展变量、发展层级和学习表现，因而基于学习进阶的评价可以较好地测评学生的现有知识储备、目前所处的学习阶段、可能存在的学习障碍、现有知识体系的缺陷等，有助于教师更好地进行学情分析，优化和改进教学过程．

为建立学习进阶所开发的测评工具就能实现上述目的．例如，研究者[12]对因数学习进阶的每个层级（参见表2）均设计了相应的试题，并给出明确的评判标准．如图1所示，对于第一道题目，如果学生能回答B和C为正确答案，则结合学生在其他题目上的表现归于第2~5层级，如果学生选择B或C为正确答案，则归入第1层级，如果学生未作答或答案包含A者，则归入第0层级．第二题的评判标准类似于第一题．这两道题目能为确立学生是否达到因数学习进阶中的第0~2层级提供依据．

1．已知甲、乙、丙都是大于0的整数，若甲´乙=丙是一个正确的乘法算式，则下列哪些选项的叙述是正确的呢？（ ）（A）甲是乙的因数（B）甲是丙的因数（C）乙是丙的因数2．已知甲、乙、丙都是大于0的整数，若甲¸乙=丙是一个正确的乘法算式，则下列哪些选项的叙述是正确的呢？（ ）（D）乙是甲的因数（E）丙是甲的因数（F）乙是丙的因数

试题来源：林哲民．国小因数与倍数学习进程研究[D]．台北：台湾师范大学，2013：117．

因数是小学数学一个极小的组成部分，它和数、数的运算、数与数之间的关系等概念和过程有密切联系．如果以学习进阶为基础体系化地构建相应的测评系统，则可以更全面地了解小学生数学学习的表现和发展．美国北卡罗莱纳州立大学教育学院的研究团队在这个方面开展了一系列的研究工作[13]．该研究团队利用学习进阶的研究成果开发了针对K-7年级学生的基于智能手机和无线技术的交互式诊断测评系统（Interactive Diagnostic Assessment System），再结合合作学习、同伴互助等学习方式改进教学，促进学生的数学学习．

表2 因数的学习进阶：假想的和修正后的

注：表格中的斜体字表示假想的与修正后的学习进阶的不同之处

3.2 学习进阶与课程

2010年美国颁布了首部“州际核心数学课程标准”（----，以下简称CCSSM），标志着美国各州采用并实施统一课程标准的开始．CCSSM内容标准的研制借鉴了学生关于数学的知识、技能和理解如何发展的学习进阶的现有研究成果[14]．这里以CCSSM中分数内容为例具体展开．

儿童分数概念的形成不是一个简单的过程．由于其表征形式的不同，分数有多种意义，具体包括连续量的部分—整体关系、离散量的子集—集合关系、除法中等分除的商、数轴上的一点、比（比值）等．许多研究表明，大多数儿童的分数概念都不完整，不了解分数的意义，对分数缺乏数意识，不知道分数是数等[15]．分数概念的形成与发展与等分、数轴等概念有很大关联．在CCSSM中分数的学习开始于小学三年级，其具体要求摘录如图2．

1．将单位分数1/b理解成把一个整体分成b个相等的部分后，每一部分可以用1/b表示；理解分数a/b是由a个1/b组成．2．将分数看作是数轴上的数，并能在数轴上表示出来．a. 在数轴上标出1/b．将数轴上0和1之间的区间看作一个整体，把它分成b等份，每一份的大小是1/b，数轴上从0开始的那一个等分点就可以标为1/b．b. 分数a/b表示在数轴上从0开始数a个1/b，得到的区间大小是a/b，其端点就是数轴上a/b的位置．

资料来源：全美州长协会和首席州立学校官员理事会．美国州际核心数学课程标准：历史、内容和实施[M]．蔡金法，孙伟，译．北京：人民教育出版社，2016：38．

图2中的标准1建立在等分的基础上，并且强调了单位分数的意义，但是显然，这里强调更多的是分数部分—整体的意义，没有凸显出分数作为一种数的理解．标准2指出分数可以用数轴上的点来表示，这样就与以前学过的整数联系起来，而且为后续要学的负数、有理数埋下伏笔．数轴的概念先前并没有正式出现，但它对学生理解整数、分数和后续出现的其它类型的数都至关重要．这里就出现了这样一个问题．如何处理数轴这样一个相对抽象的概念？直接给出数轴的数学定义显然是不现实的，中国人教版数学教材在七年级才正式出现数轴的概念．有关测量和长度的学习进阶研究[16-17]指出数轴可以作为一个直观的测量工具出现．例如Clements和Sarama[18]强调测量可以联系形和数，指出测量与诸如传递性、等分、单位、标准单位的迭代、距离的累积、原点等基本概念或技能之间有重要关联，约八岁的儿童就可以利用尺子建立自己的测量单位，并对所要测量的对象进行分割，然后再对每一段进行估计．由此，CCSSM将数轴与测量联系起来，并在小学一年级和二年级就加以渗透，为三年级“将分数看作是数轴上的数”中的数轴内容作铺垫．图3给出了CCSSM一年级和二年级与数轴有关的测量内容的学习要求．一年级和二年级的标准中包含单位长度及用单位长度测量物体长度，并建立整数及其运算与长度表示之间的关系，这些内容为学生理解数轴的单位长度、方向、原点等要素提供了重要的直观经验．

上述关于数轴内容的处理展示了CCSSM数学内容的编排顺序如何借鉴了与学生随着时间推移获得和发展数学知识、技能和理解能力的实证研究成果．学习进阶的研究为课程标准的内容安排提供了强有力的支撑．

3.3 学习进阶与教学

将学习进阶应用于课堂教学的关键在于如何将学习进阶的理论知识转化为教师在课堂上可以直接应用的教学实践．美国教育政策研究联盟（Consortium for Policy Research in Education，简称为CPRE）[10]给出了如图4所示的框图，并指出转化的核心在于开发基于学习进阶的、能直接用于课堂教学实践的工具和资源．这里以整数的乘法为例进行介绍．

一年级通过将多个相同的小物体（长度标准）首尾相连，把一个物体的长度表示为该长度标准的整数倍；理解测量物体的长度就是用相同大小的单位长度，没有间隙、没有重叠地进行覆盖，所用长度标准的数量就是测量的结果（局限于所需长度标准的个数为整数的物体）．二年级1．选择和使用恰当的工具测量物体的长度，如直尺、码尺、米尺和卷尺等．2．用两个不同的长度单位测量同一物体；描述两次测量的结果与所选长度单位大小之间的关系．3．用不同的单位（如英寸、英尺、厘米和米）对长度进行估计．4．通过测量，用标准长度表示一个物体比另一物体长多少．5．用100以内的加减法解决长度单位相同的文字题．例如，借助图示（如画尺子来量长度的图）或用符号表示未知量的等式来表征问题．6．在一条直线上借助长度表示从0开始的整数，等间距的点依次表示0, 1, 2,…，并在直线上表示出100以内的和与差．

资料来源：全美州长协会和首席州立学校官员理事会．美国州际核心数学课程标准：历史、内容和实施[M]．蔡金法，孙伟，译．北京：人民教育出版社，2016：29，33．

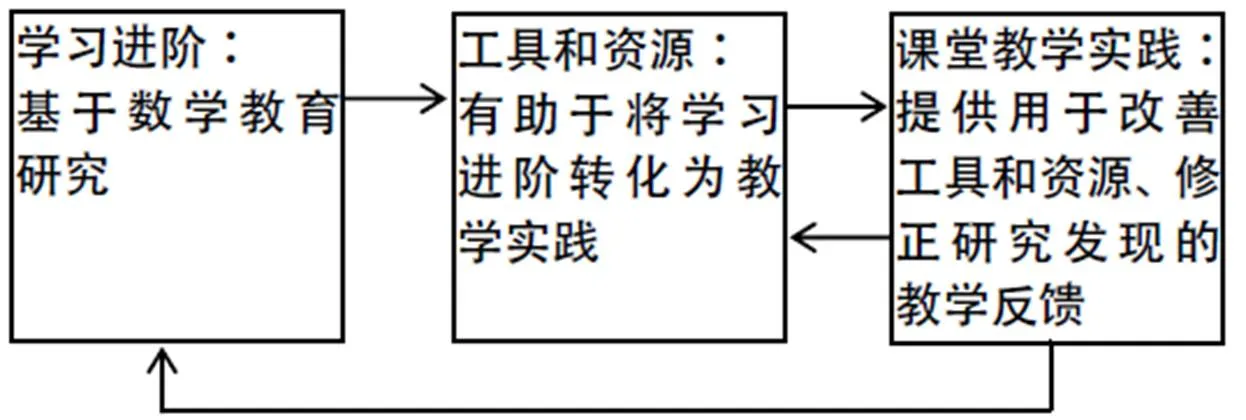
图4 从学习进阶研究的理论知识到课堂实践的转化

资料来源：DARO P, MOSHER F A, CORCORAN T. Learning trajectories in mathematics: a foundation for standards, curriculum, assessment, and instruction [EB/OL]. (2015-06-03) [2016-11-20]. Consortium for Policy Research in Education, 2011.http://www.cpre.org/sites/default/files/researchreport/1220_learningtrajectoriesinmathcciireport.pdf.DOI:10.12698/cpre. 2011. rr68.

有这样一道应用题，学校图书馆买了6捆书，每捆有25本，一共有多少本书？有的学生在解答时采用了连加的解题策略，即25+25+25+25+25+25=150，给出了正确答案150本．虽然答案正确，但这些学生还未掌握乘法策略，不利于后继与乘法推理有关的小数乘法、比例等内容的学习．明确了学生的认知起点，该如何进行有针对性的课堂教学？这里就需要有相应教学工具和资源的支持．美国佛蒙特州数学评价研究项目开发了一个如图5所示的针对乘法内容的教学框架[10]，引导教师如何根据学生情况进行教学．

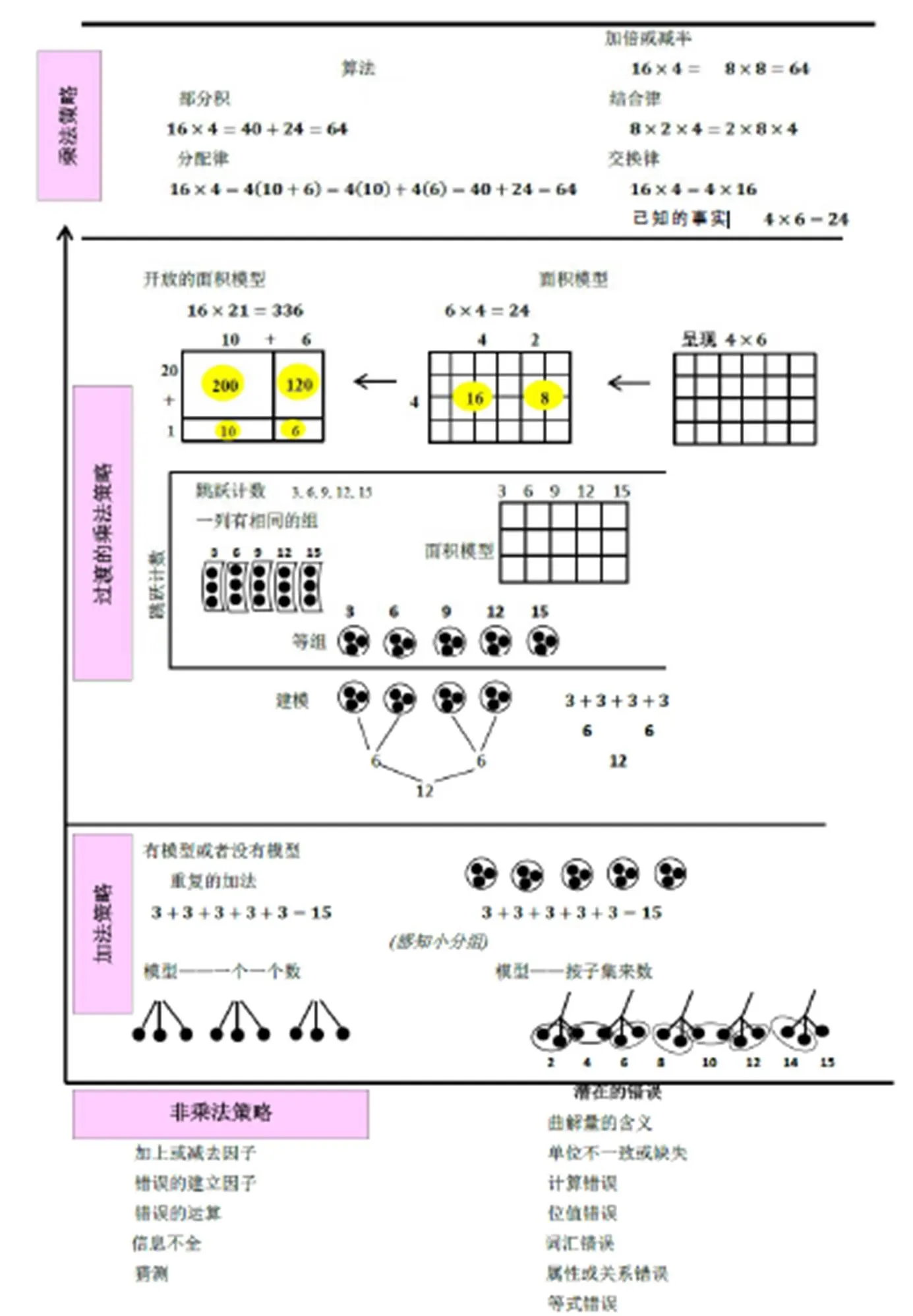
图5 乘法教学框架

资料来源：同图4．

该框架包括3个要素：（1）描述学生乘法理解如何发展的学习进阶，即非乘法策略—早期加法策略—过渡的乘法策略—乘法策略；（2）每个阶段影响学生问题解决的任务结构和相关联的概念过程分析等；（3）阻碍学生理解新概念或掌握新策略的可能的错误、误解或前概念．根据情境、数值大小或数值个数等问题结构要素的变化，学生采用的策略可能会在乘法策略、过渡的乘法策略和加法策略中间来回往复．如果通过形成性测评发现学生处于加法策略的阶段，教师可逐步利用框架中过渡的乘法策略和乘法策略阶段的任务进行教学，帮助学生实现从加法策略到乘法策略的发展．该框架有助于教师更好地理解学生的学习表现，并在学生现有基础上进行课堂教学活动的设计和实施．

总的来说，基于学习进阶的课堂教学不仅遵循了学生的数学认知发展规律，而且有助于教师通过作业、课堂表现等分析确定学生的理解达到了哪一个层次、可能存在的学习障碍和误区，使教学更具针对性，而学习进阶的理论知识和课堂教学实践之间的桥梁，即教学工具和资源的开发，就尤为重要．事实上，如图5所示的乘法教学框架的建立并不是一项简单的工作，其关键在于数学任务的设计和实施，需要教育研究发现和教学实践检验的不断融合和调整，也需要有教师专业发展活动的支持和引导．

4 对中国学习进阶研究的启示

根据2017年9月4日在中国知网上以“学习进阶”为关键词进行文献检索后发现，共有相关文献98篇，其中学术期刊论文79篇，硕士学位论文16篇，博士学位论文3篇．关于学习进阶的论文最早发表于2012年，之后逐年增加，表明学习进阶研究在我国虽处于起步阶段但正逐渐受到重视．从内容来看，这些论文中近五分之四聚焦在学习进阶的理论和应用的介绍上，剩余的五分之一是关于建立某概念学习进阶的实证研究，以硕博学位论文为主．从涉及的学科领域来看，这些论文几乎都是关于物理、化学和生物的，关于数学学科领域内的学习进阶研究非常稀缺．从研究方法来看，大部分论文是讨论式的、介绍性的，只有少数论文采用了实证方法．基于中国学习进阶研究的现状和上述数学教育中学习进阶研究的进展，特提出以下3点建议．

第一，要充分认识学习进阶在数学教育中的理论价值和实践意义．学习进阶刻画了学生在一个较大时间跨度内对某一学习主题的认识、理解和实践从简单到复杂、从低水平到高水平的发展过程，能有效联系数学教育研究和教学实践中的评价、课程、教学问题，对教师培养也有重大意义．从评价角度来看，要凸现学习进阶在描述学生学习表现上的发展性和阶段性特点，诊断学生的层级水平和错误类型，为开展有针对性的诊断式教学做好准备；从课程角度来看，要科学安排课程内容的教学顺序和学习要求，以学习进阶的理论为依托促进课程的连贯性；从教学角度来看，要根据学生现有的学习表现和层级水平明确教学目标，有的放矢地设计和实施教学任务、开展教学活动，积累有助于将学习进阶理论转化为教学实践的教学工具和资源．与此同时，学习进阶的理论和实践，尤其是与数学的课程、教学和评价整合之后的理论和实践，有利于数学教师理解学生关于某学习主题的认知发展过程，厘清课程的发展脉络，更好地使用评价工具服务课堂教学，反之，教师的课堂教学实践能促进其对学习进阶相关理论和研究发现的深入认识和理解，实现理论与实践的相辅相成，协同进步．

第二，以实证方法建立描述学生关于某一学习主题认知纵深发展的学习进阶是数学教育领域学习进阶研究的基础．从中国目前有关学习进阶的研究来看，实证研究相当缺乏，亟待改变．此外，学习进阶的建立是学习进阶与数学课程、教学和评价整合的基础，只有明确了某一学习主题下学习进阶的发展变量、发展层级和学习表现，才能有效思考和研究学习进阶的研究发现如何应用至数学课程连贯性的建立、诊断性评价研究的深入，以及针对性课堂教学的设计和实施．在数学教育研究领域，有大量关于学生就某一数学概念、过程或能力的学习表现的横切面式的调查研究，但缺乏从纵深层面就学生对某一概念是如何发展的实证研究．美国北卡罗莱纳州立大学教育学院的研究团队针对小学和初中年级主要数学内容建立了计数、分数、机会和概率、位值制和小数等18个核心概念的学习进阶，取得了一系列研究成果[19-22]，可以作为开展类似研究的参考．

第三，积极推广学习进阶的研究成果在数学课程、教学和评价等领域的应用性研究．从上文介绍的学习进阶在数学教育领域中的应用性研究示例中可以看到，学习进阶不仅能促进课程内容编排的有序性和连贯性，还能诊断学生现有知识储备、发展层级、可能存在的学习障碍、现有知识体系的缺陷等，使教师能更好地进行学情分析，课堂教学更具针对性和更有效率．进一步地，学习进阶融入教师教育后，还能促进教师对学生思维的深入了解和自身数学学科知识和数学教学知识的发展．

[1] SONGER N B, KELCEY B, GOTWALS A W. How and when does complex reasoning occur? Empirically driven development of a learning progression focused on complex reasoning about biodiversity [J]. Journal of Research in Science Teaching, 2009 (7): 611-631.

[2] MERRITT J D, KRAJCIK J, SHWARTZ Y. Development of a learning progression for the particle model of matter [EB/OL]. (2016-10-01) [2016-11-20]. http://www.umich.edu/~hiceweb/presentations/documents/Merritt_et_al_ICLS_ 2008_vFINAL.pdf.

[3] SALINAS I. Learning progressions in science education: two approaches for development [C]. Iowa City IA: Learning Progressions in Science Conference, 2009: 56-98.

[4] DUNCAN R G, HMELO-SILVER C E. Learning progressions: aligning curriculum, instruction and assessment [J]. Journal of Research in Science Teaching, 2009, 46(6): 606-609.

[5] SMITH C L, WISER M, ANDERSON C W, et al. Implication of research on children’s learning for standards and assessment: a proposed learning progression for matter and the atomic molecular theory [J]. Measurement: Interdisciplinary Research and Perspectives, 2006 (4): 1-4.

[6] ROSEMAN J E, CALDWELL A, GOGOS A, et al. Mapping a coherent learning progression for the molecular basis of heredity [C]. San Francisco, CA: The annual meeting of the national association for research in science teaching, 2006: 3.

[7] ALONZO A, STEEDLE J. Developing and assessing a force and motion learning progression [J]. Science Education, 2009, 93(3): 389-421．

[8] NATIONAL RESEARCH COUNCIL (NRC). Taking science to school: learning and teaching science in grades K-8 [M]. Washington: National Academies Press, 2007: 36.

[9] BATTISTA M T. Conceptualizations and issues related to learning progression, learning trajectories, and levels of sophistication [J]. The Mathematics Enthusiast, 2011 (8): 507-569.

[10]  DARO P, MOSHER F A, CORCORAN T. Learning trajectories in mathematics: a foundation for standards, curriculum, assessment, and instruction [EB/OL]. (2015-06-03) [2016-11-20]. Consortium for Policy Research in Education, 2011. http://www.cpre.org/sites/default/files/researchreport/1220_learningtrajectoriesinmathcciireport.pdf. DOI:10.12698/cpre. 2011.rr68

[11]  CORCORAN T, MOSHER F A, ROGAT A. Learning progressions in science: an evidence-based approach to reform [M]. Philadelphia: Consortium for Policy Research in Education, 2009: 222-224.

[12] 林哲民．国小因数与倍数学习进程研究[D]．台北：台湾师范大学，2013：66-150．

[13]  CONFREY J, MALONEY A P. A design research study of a curriculum and diagnostic assessment system for a learning trajectory on equipartitioning [J]. ZDM–The International Journal on Mathematics Education, 2015 (47): 919-932.

[14]  CCSSO/NGA. Common core state standards for mathematics [M]. Washington, DC: Council of Chief State School Officers and the National Governors Association Center for Best Practices, 2010: 4.

[15] 鲍建生，周超．数学学习的心理基础与过程[M]．上海：上海教育出版社，2009：243-246．

[16]  CLEMENTS D H. Teaching length measurement: research challenges [J]. School Science and Mathematics, 1999, 99(1): 5-11.

[17]  NUNES T, LIGHT P, MASON J H. Tools for thought [J]. Learning and Instruction, 1993, 3(1): 39-54.

[18]  CLEMENTS D, SARAMA J. Learning and teaching early mathematics: the learning trajectories approach [M]. New York: Routledge, 2009: 89.

[19]  ANDREW K C. A design study of co-splitting as situated in the equipartitioning learning trajectory [D]. Raleigh, NC: Unpublished doctorate thesis, North Carolina State University, 2013: 36-78.

[20]  CONFREY J, MALONEY A, NGUYEN K H, et al. Equipartitioning a foundation for rational number reasoning: elucidation of a learning trajectory [M] // MALONEY A P, CONFREY J, NGUYEN K H. Learning over time: learning trajectories in mathematics education. Charlotte: Information Age, 2014: 61-96.

[21]  WILSON P H. Teachers’ uses of a learning trajectory for equipartitioning [D]. Raleigh, NC: Unpublished doctorate thesis, North Carolina State University, 2009: 98-156.

[22]  EDGINGTON C. Teachers’ uses of a learning trajectory as a tool for mathematics lesson planning [M] // LO J J, LEATHAM K R, VAN ZOEST L R. Research trends in mathematics teacher education. Switzerland: Springer International Publishing, 2014: 261-284.

[责任编校：周学智]

Progress and Implications of Learning Progression Research in Mathematics Education

WU Ying-kang, DENG Shao-bo, YANG Jie

(Mathematics department, East China Normal University, Shanghai 200241, China)

The idea of learning progression origins from science education in the United States. From the global perspective, learning progression research in mathematics education has just begun, and it could be generally classified into two big categories. The first category concerns on basic research on learning progression, that is, building the learning progression of certain mathematical learning theme to describe students’ longitudinal development of understanding using empirical methods, and the other category involves applying learning progression into mathematics assessment, curriculum and instruction. On the basis of a brief introduction of its concept and characteristics, this paper describes how the learning progression of factor, a primary mathematics concept, had been established, and presents research examples of applying learning progression into mathematics assessment, curriculum and instruction. These examples not only demonstrate the theoretical and practical significance of learning progression research in mathematics education, but also reveal the approach of carrying out research in this field.

learning progression; mathematics education; research; implication

G622

A

1004–9894（2017）06–0040–07

吴颖康，邓少博，杨洁．数学教育中学习进阶的研究进展及启示[J]．数学教育学报，2017，26（6）：40-46．

2017–06–12

2015年度上海市教育科学研究重大项目——中小学数学教材的有效设计之子课题中小学数学课程内容发展主线的顶层设计（D1508）；上海市科学技术委员会资助课题——核心数学与实践（13dz2260400）；教育部人文社会科学重点研究基地重大项目——中国学生数学素养测评研究（16JJD880023）

吴颖康（1975—），女，上海人，副教授，主要从事数学教师教育和学校统计教育研究．