八年级学生数学概念表征及其对学业成绩的影响机制——基于Z省的大规模测试
2017-12-22何声清綦春霞
何声清,綦春霞
八年级学生数学概念表征及其对学业成绩的影响机制——基于Z省的大规模测试
何声清1,綦春霞1,2
(1.北京师范大学 教育学部,北京 100875;2.北京师范大学 未来教育高精尖创新中心,北京 100875)
依托大规模纸笔测试,以Z省34 412名八年级学生为被试考察数学概念表征及其对学业成绩的影响机制.结果表明,概念表征得分排序从高到低依次是符号表征、语言表征、图象表征及结构表征;男生结构表征显著优于女生,女生在其它表征方面均显著优于男生;结构表征通过其它表征对数学学业成绩及各内容领域成绩的间接影响均达显著,且贡献大于直接影响;在间接影响路径中,通过符号表征的影响最大,通过语言表征的影响次之;概念表征对三大内容领域的影响机制存在差异.对课程与教学的建议有:关注学生数学体系的整体建构;培养学生多元表征及其相互转化的能力;重视数学符号意识及数学交流能力的培养;关注概念表征对不同内容领域学业成绩影响的差异;关注概念表征的性别差异.
八年级;符号表征;图象表征;语言表征;结构表征;学业成绩
1 问题提出
除了理论分析以外[9-12],中国研究者已然对学前[13]、小学[14-15]、初中[16-17]及高中[18-19]阶段学生数学概念表征的现状及年级差异[20-21]、群体差异[22-23]、影响因素[24-26]等进行了诸多实证研究.此外,已有研究也一再证实了概念表征对于数学概念理解[27-28]、问题解决[29-30]及学业成绩[31-32]的积极影响.数学概念的表征具有多元性[33].数学学业测试在知识和能力要求上则具有综合性,而当前有关数学概念表征对学业成绩影响的研究多聚焦于某一类表征,尚缺乏多元表征对学业成绩影响及其具体机制的考察.此外,数学学科的不同内容领域在概念表征的侧重上有所差异,因此各类表征对不同内容领域的影响机制也可能存在差异.除了上述具体形式的表征之外,对数学知识结构、体系的整体把握是知识建构的必要前提[34].例如,有关概念图[35-37]、数学联接[38-39]、变式教学[40-41]等领域的研究都一再表明,整体把握知识之间的结构(层级关系、包含关系、类比关系,等)对数学概念的形成和发展有重要意义.在学业测试等综合性的测试中,也应将概念的结构表征置于其他具体表征之前.鉴于此,通过构建数学概念表征对学业成绩影响的模型,依托中国基础教育质量监测的大规模纸笔测试,考察八年级学生数学概念表征及其对学业成绩的影响机制,并据此对课程和教学提出相应建议.
2 研究方法
2.1 被试
基于大规模纸笔测试从Z省收集数据,该省是中国东部某发达省份,其经济、教育基本处于上等水平.采取分层随机取样方法,从该省11个市的城市、县城、乡镇3类地区抽取八年级被试34 412名,其中男性被试18 033名,女性被试16 379名.选取八年级学生为被试的原因是,国际范围内的数学学业成就测试(如,TIMSS[42]和PISA[43])均以八年级为对象,这为中国数学学业质量监测提供了理论和实践基础.
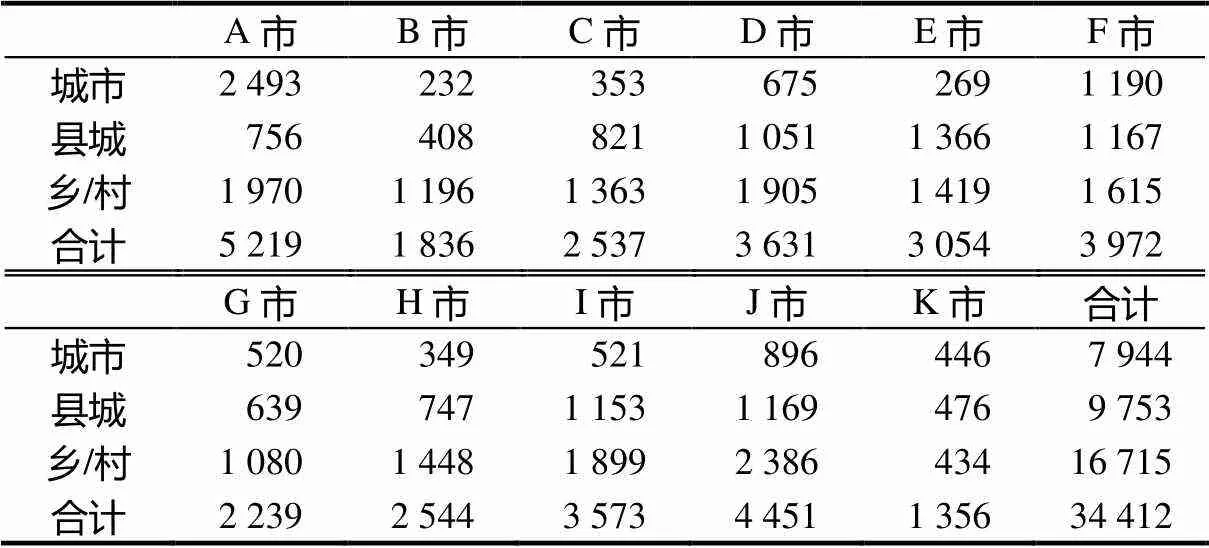
表1 被试情况
2.2 测试工具
(1)概念表征问卷.
结合八年级学生的认知水平和测试需要,对已有的概念表征模型进行适当修订,形成了包含符号表征、图象表征、语言表征及结构表征的四维表征问卷.其中,符号表征是指用数学符号、公式等解释和理解数学概念;图象表征是指用画图、列表等解释和理解数学概念;语言表征是指用语言文字解释和理解数学概念;结构表征是指通过将当前概念与其它概念联系、对比等理解数学概念.以函数=2+1为例,4类表征的基本形式如图1.
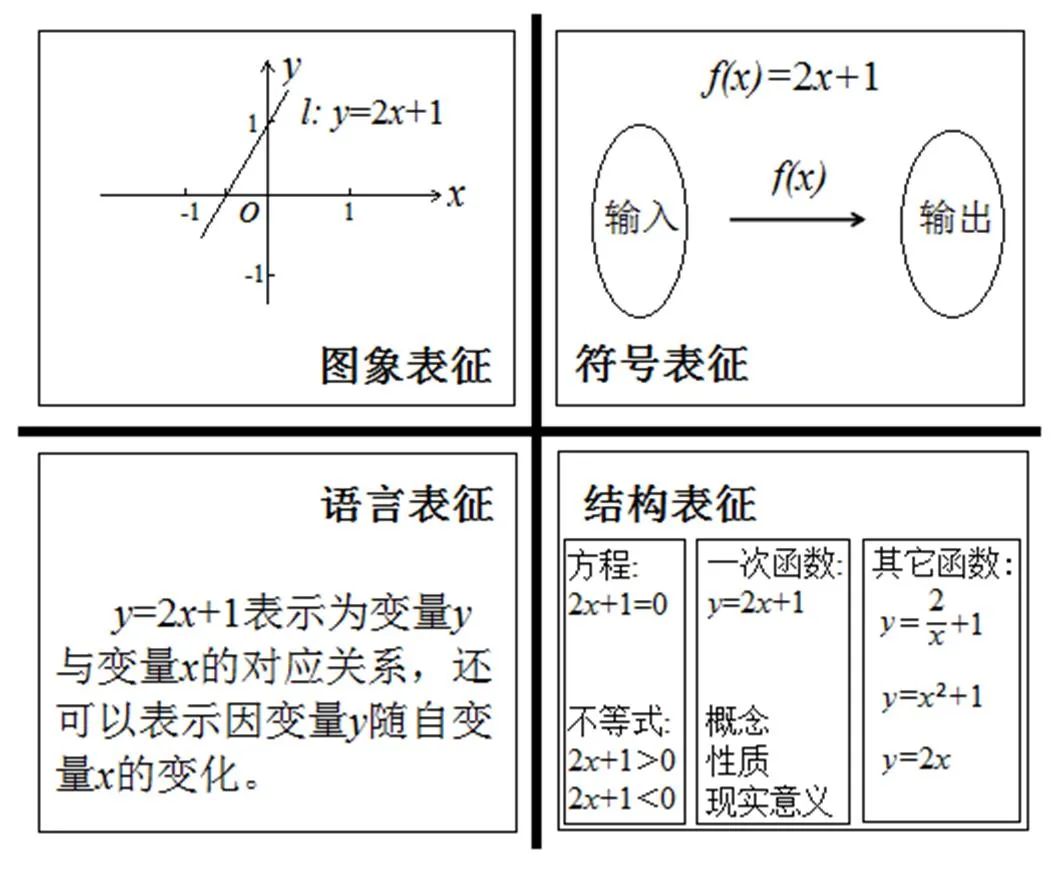
图1 函数概念的多元表征
内部一致性系数分析表明,问卷具有较高的同质性信度(=0.759).
(2)数学学业测试.
数学学业测试以《义务教育数学课程标准(2011年版)》为依据,结合现行教材的内容设置,从内容维度(数与代数、图形与几何及统计与概率)和认知维度(了解、理解、掌握及运用)两方面考察八年级学生数学学业表现.以A卷M8AO061题为例,该题在内容维度上属于“数与代数”,在认知维度上属于“理解”,主要考察学生利用函数图象刻画变量间关系的能力,在情境设置上贴近生活实际和日常经验.
小晴在荡秋千,在不加推力的情况下,可以描述她荡秋千过程中高度随时间变化的图象是( ).
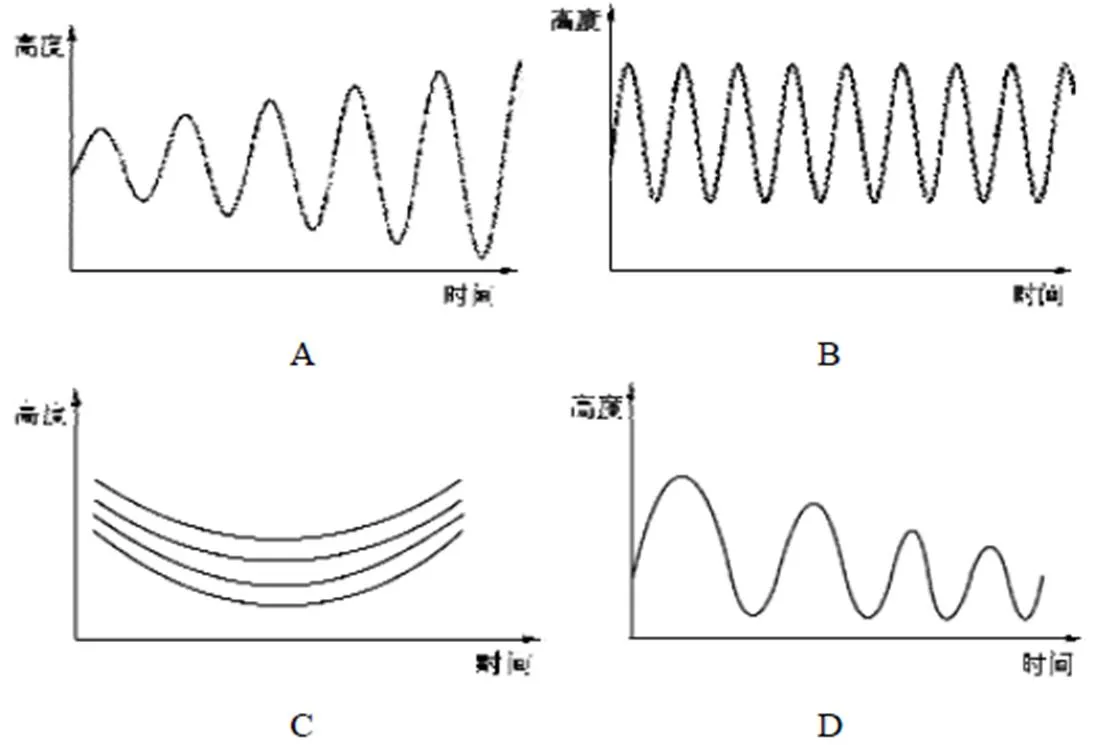
在该测试中,使用了A、B两套平行卷,每一个测试题目都明确厘定了其考察的内容维度和认知维度并进行了编码.内部一致性系数分析表明,两套测试卷均具有较高的同质性信度(A卷=0.908;B卷=0.897).
(3)测试程序.
借鉴国际大规模测试的经验,命题组在从试题设计到组织施测的过程中,先后经历了组建命题专家队伍、制定测试方案、编制测试框架及细目表、征集题目、6人访谈、300人预测试、国际专家评审等环节,其间几易其稿,明确了每个测试题考察的内容和能力水平,确保了测试的科学性和规范性[44].
(4)模型构建.
鉴于综合性测试对学生数学知识的整体考察,将结构表征作为影响学业表现的直接变量();鉴于不同数学内容领域知识在表征形式(符号表征、图象表征、语言表征)侧重上有所差异,将上述3类表征作为影响学业成绩的间接变量(分别记为1、2、3).
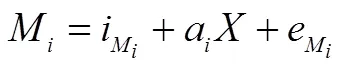
3 研究结果
3.1 八年级学生数学概念表征的倾向性
对Z省八年级学生数学概念表征进行总体分析,数学概念表征得分从高到低依次是符号表征(=3.4,=0.811)、语言表征(=3.28,=0.854)、图象表征(=3.21,=0.859)及结构表征(=2.76,=0.948).
为进一步证实八年级学生概念表征倾向性的差异,对Z省11个地级市八年级学生数学概念表征进行具体分析(图2),各市学生数学概念表征的得分排序基本一致,从高到低依次均是符号表征、语言表征、图象表征及结构表征.这再一次说明,八年级学生对于符号表征的倾向性较高,而结构表征的倾向性较低.
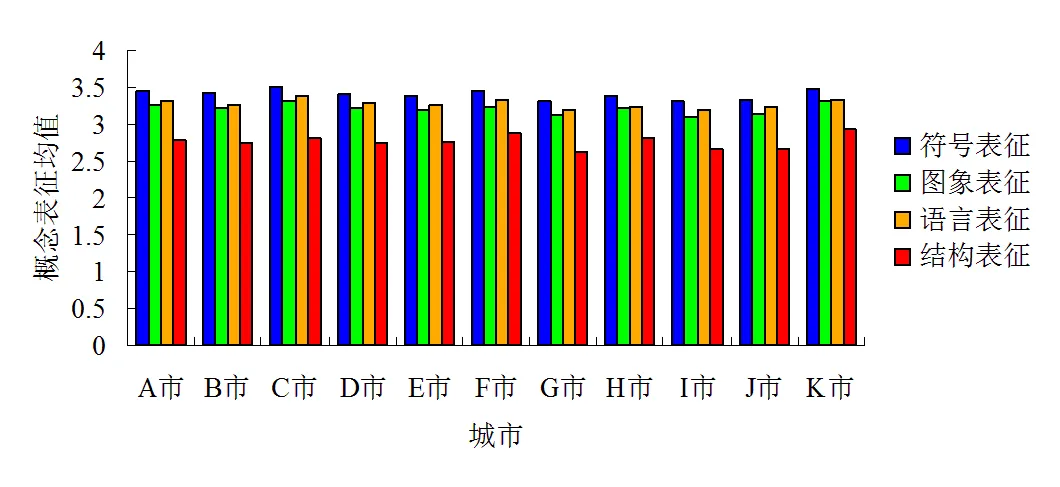
图2 Z省11个地级市八年级学生数学概念表征倾向性比较
男、女生概念表征的得分排序也基本一致,从高到低依次均为符号表征、语言表征、图象表征及结构表征(图3).
对不同性别学生概念表征得分进行差异检验,男生结构表征显著优于女生(Δ=0.09,=8.835,<0.001),女生在符号表征(Δ=-0.111,=-12.787,<0.001)、图象表征(Δ=-0.156,=-16.913,<0.001)及语言表征(Δ=-0.074,=-8.02,<0.001)方面均显著优于男生.

图3 男女生概念表征倾向性比较
3.2 概念表征对数学学业成绩的影响
(1)描述性统计结果.
若不考虑人口学变量“性别”,其他关涉变量间均存在显著性正相关(所有<0.001).具体而言(表2),数学总分与各类表征的相关介于0.15~0.27之间,三大内容领域得分与各类表征的相关介于0.088~0.252之间,说明学生的数学学业成绩及各内容领域的学业成绩均与学生的概念表征密切相关,符合理论预期.此外,性别与数学学业成绩、各内容领域成绩及概念表征之间均存在显著性相关(所有<0.001),因此在后续分析中将其作为控制变量.
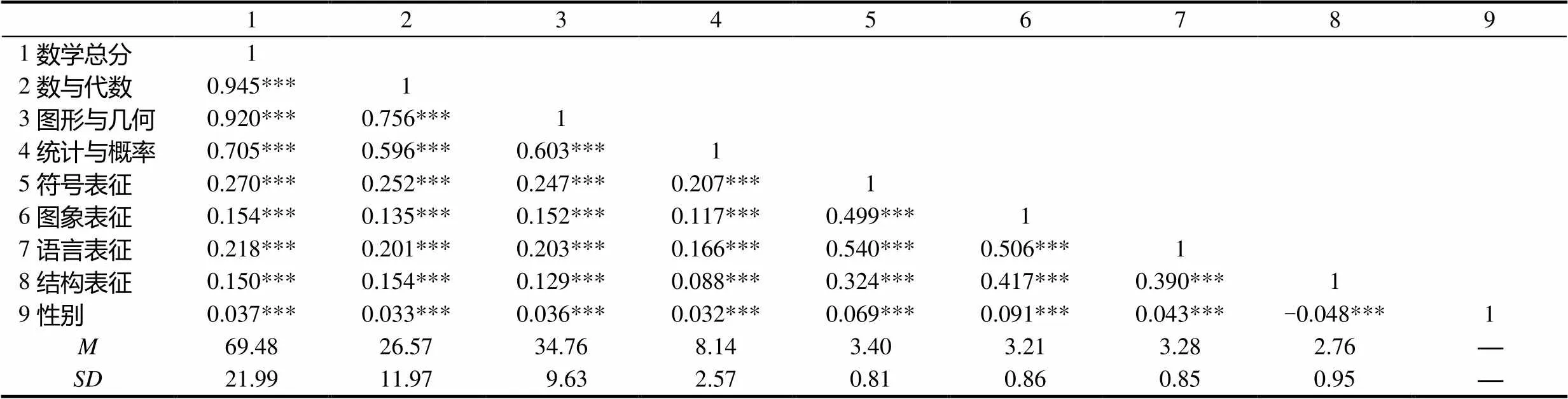
表2 关涉变量的均值与标准差及相关系数
注:***表示<0.001
(2)概念表征对数学学业成绩的影响机制.
以性别为控制变量,以结构表征为自变量,以符号表征、图象表征及语言表征为中介变量,以数学总分为因变量,采用Bootstrap方法重复抽样5 000次进行回归系数的显著性检验,以获得参数估计的稳健标准误()及95%偏差校正的信赖区间(),结果如表3所示.
结构表征对符号表征(1=0.281,=0.272~0.289)、图象表征(2=0.383,=0.374~0.391)及语言表征(3=0.354,=0.346~0.363)均有显著的直接正向影响,对数学总分(=1.313,=1.045~1.58)也有显著的直接正向影响.符号表征(1=5.694,=5.349~6.039)及语言表征(3=2.402,=2.068~2.736)对数学总分均有显著的直接正向影响,图象表征(2=-0.632,=-0.96~-0.304)对数学总分有显著的直接负向影响.
结构表征通过符号表征(11=1.597,=1.478~1.718)及语言表征(33=0.851,=0.723~0.981)对数学总分有间接正向影响且均达显著,通过图象表征(22=-0.242,=-0.374~-0.117)对数学总分有间接负向影响且达显著.
整体而言,结构表征对数学学业成绩的直接影响(1=1.313,=1.045~1.58,效应量为37.3%)及间接影响(2=2.207,=2.049~2.361)均达到显著.在3条间接影响路径中,通过符号表征的影响最大(效应量为45.37%),通过语言表征的影响次之(效应量为24.18%),通过图象表征有一定负向影响,且上述路径之间差异显著(符号-图象=1.839,=1.648~2.038;符号-语言=0.746,=0.547~0.944;图象-语言=-1.093,=-1.297~-0.895).
(3)概念表征对数学内容领域成绩的影响机制比较.
以性别为控制变量,以结构表征为自变量,以符号表征、图象表征及语言表征为中介变量,分别以“数与代数”、“图形与几何”及“统计与概率”三大内容领域得分为因变量,采用Bootstrap方法重复抽样5 000次进行回归系数的显著性检验,以获得参数估计的稳健标准误()及95%偏差校正的信赖区间(),结果如表4所示.

表3 概念表征对数学学业成绩的影响机制分析
注:各系数均为非标准化值,下同

表4 概念表征对数学三大内容领域的影响机制比较
注:结构表征,1符号表征,2图象表征,3语言表征
概念表征对三大内容领域的影响机制存在差异.在“数与代数”领域,结构表征对该领域成绩的直接影响(1=0.929,=0.783~1.076)及间接影响(2=1.03,=0.947~1.113)均达显著.在3条间接影响路径中,通过符号表征的影响最大(11=0.833,=0.768~0.895),通过语言表征的影响次之(33=0.414,=0.346~0.484),通过图象表征有一定负向影响(22=-0.217,=-0.284~-0.145),且上述路径之间差异显著(符号-图象=1.05,=0.943~1.152;符号-语言=0.419,=0.312~0.524;图象-语言=-0.63,=-0.741~-0.526);在“图形与几何”领域,结构表征对该领域成绩的直接影响(1=0.358,=0.24~0.476)及间接影响(2=0.961,=0.891~1.029)均达显著.具体而言,通过图象表征的影响未达显著(22=-0.013,=-0.068~0.044),在两条显著的影响路径中,通过符号表征的影响最大(11=0.619,=0.567~0.673),通过语言表征的影响次之(33=0.355,=0.297~0.411),且两条路径之间差异显著(符号-语言=0.263,=0.176~0.352);在“统计与概率”领域,结构表征对该领域成绩的直接影响(1=0.025,=-0.007~0.057)不显著,间接影响(2=0.216,=0.198~0.235)达到显著.具体而言,通过图象表征的影响未达显著(22=-0.012,=-0.027~0.003),在两条显著的影响路径中,通过符号表征的影响最大(11=0.146;=0.132~0.161),通过语言表征的影响次之(33=0.082;=0.066~0.097),且两条路径之间差异显著(符号-语言=0.064;=0.041~0.088).
进一步,就概念表征对数学三大内容领域的影响路径效应量进行了比较(表5).结果表明,在“数与代数”领域,结构表征对学业成绩的直接影响最强,其效应量近乎所有影响路径的一半;通过符号表征的间接影响次之,其效应量达到40%以上;通过语言表征的间接影响最小,通过图象表征的间接影响意义不大.在“图形与几何”领域,结构表征通过符号表征对学业成绩的间接影响最强,其效应量近乎所有影响路径的一半;结构表征的直接影响与其通过语言表征的间接影响相当.在“统计与概率”领域,结构表征通过符号表征的间接影响最强,其效应量高达60%以上;结构表征通过语言表征的间接影响次之;结构表征的直接影响及其通过图象表征的间接影响均未达显著.可见,符号表征在所有内容领域学业成绩的影响路径中均有显著且较高的中介作用;语言表征在所有内容领域学业成绩的影响路径中也均有显著的中介作用但效应量相对较低;符号表征在所有内容领域学业成绩的影响路径中均无显著的正向中介作用;结构表征对“数与代数”及“图形与几何”领域学业成绩有直接的正向作用,但对“统计与概率”领域的直接效果则未达显著.

表5 概念表征对数学三大内容领域的影响路径效应量比较
注:结构表征,1符号表征,2图象表征,3语言表征;效应量仅作各内容领域的内部比较
4 讨论与建议
4.1 关注学生数学体系的整体建构
结构表征对数学学业成绩及各内容领域(除“统计与概率”以外)的直接影响均达显著,但学生结构表征得分相对较低.建构主义认为,数学学习是通过建立新旧知识之间的联系,将新知识纳入原有知识体系或将原有知识适当改造以适应新知识的过程.换言之,学生对于某概念的理解除了能够在概念的符号表征、语言表征及图象表征之间进行内部转换之外,还应能将该概念纳入到更大的知识谱系中与其它的概念进行比较、区分或融合.尤其在数学问题解决及综合性测试中,学生更需要综合头脑中已经习得的概念,进行适当提取和运用.“结构表征最有利于元认知监视和正确解题,是最佳的表征方式.”[45]以几何证明为例,面临名目繁多的定义、命题、基本事实、定理等(如“过直线外一点有且只有一条直线与这条直线平行”,“角平分线上的点到角两边的距离相等,角的内部到角两边距离相等的点在角的平分线上”),学生要对其进行语言表征,将书面的知识进行内化;在证明的过程中,学生需要用运算符号刻画逻辑演绎的过程,这需要学生对知识进行符号表征;证明过程常常需要学生进行作图、添加辅助线、借助几何直观等,这涉及到知识的图象表征.然而,仅仅局限于以上,几何证明常常寸步难行,而更加需要学生对各个性质、定理进行全面联系和体系建构,在头脑的知识体系中合理选择论证依据,几何证明才能水到渠成.
4.2 培养学生多元表征及其交互的能力
数学概念的多元表征协同影响了数学学业成绩.结构表征尽管对综合性的学业测试有直接影响(37.3%),但它的影响更多地是通过其它表征而间接实现(62.7%).“统计与概率”领域的学业成绩甚至完全依赖于结构表征的间接影响,这或许因为义务教育阶段所涉及的该领域内容不多,学生对其尚未发展成系统的知识结构,进而其它表征的作用被凸显.概念的多元表征及其交互对数学学习有积极影响,这也得到了相关研究的支撑:概念表征间的转换和交互能加深数学理解[46]及有助于问题解决[47].不同的表征形式反映了概念的不同侧面,从整合的表征中获取的信息比从单一的表征中获取的要多[48].仍以函数概念为例,它有4种基本的表征形式(列表、公式、图象及语言).其中列表形式的函数比较直观地呈现了自变量和因变量的对应关系,但是不利于进行运算;公式形式是函数最抽象的表征方式,它简要地刻画了变量之间的数学关系;图象形式是函数最直观的表征方式,它不仅刻画了自变量和因变量的对应关系,更生动地描述了两者的相依及变化关系;语言形式是用文字描述函数的概念和意义,是学生理解函数概念必要的环节.此外,《课程标准(2011年版)》还对函数概念各类表征的适当选择及其相互转换提出了基本要求[8]:“能用适当的函数表示法刻画简单实际问题中变量之间的关系”;还强调了生活背景(现实情境表征)对于函数概念理解的重要意义,指出“能举出函数的实例,能结合图象对简单实际问题中的函数关系进行分析”.
4.3 重视数学符号意识及数学交流能力的培养
在结构表征的基础上,符号表征及语言表征对学业成绩的中介效果均达显著;在“图形与几何”及“统计与概率”领域,通过符号表征的间接效果贡献甚至大于结构表征的直接效果.符号表征是数学抽象化过程中的必要环节,仅仅停留在数学的直观表征层面则无法企及数学概念的深层次理解.数学交流是指学生用自己的语言对数学概念、观点等进行阐述,是一个对数学概念深度内化的过程,能够帮助学生获得对数学概念的个性化理解.《课程标准(2011年版)》对上述两类表征都做了明确的强调[8],把“符号意识”作为学生数学能力的十个关键词之一,“符号意识是指能够理解并且运用符号表示数、数量关系和变化规律;知道使用符号可以进行运算和推理,得到的结论具有一般性.建立符号意识有助于学生理解符号的使用是数学表达和进行数学思考的重要形式.”在“综合与实践”中则提出“会反思参与活动的全过程,将研究的过程和结果形成报告或小论文,并能进行交流.”
4.4 关注概念表征对不同内容领域学业成绩影响的差异
概念表征对数学三大内容领域的影响路径效应量存在较大差异,这也基本符合各内容领域知识属性的特征:中学阶段“数与代数”领域知识量较大且基本形成了前后连贯的知识体系,这对学生的结构表征提出了较高要求;其承载的核心能力主要有数感、符号意识、运算能力、模型思想、推理能力等,这对学生的符号表征及语言表征提出了较高的要求.“图形与几何”领域在知识量上也有较大比重,符号化的几何证明是该领域的特征之一,这对学生的符号表征提出了较高要求;此外,该领域的核心目标之一是逻辑推理能力的培养,而在演绎推理的语境之下,除了符号表征以外,学生的语言表征能力也扮演着重要角色;当然,该领域充斥着大量的性质、定理且它们之间存在严格的逻辑递进关系,这需要学生在其知识体系中形成相对系统的结构表征,以便在逻辑推理中灵活运用;比较意外的是,该领域还承载着几何直观、空间观念等能力的培养,然而图象表征对该领域学业成绩的间接影响未达显著.“统计与概率”领域在知识量上相对较少,且义务教育阶段在该领域内容的设置上相对松散,更多的该领域知识在高中阶段才正式学习.在综合性测试中,该领域知识的考查范围也常常有限,对学生的结构表征相对而言没有过高的要求,因而结构表征对该内容领域学业成绩的直接影响未达显著.尽管如此,该领域承载着数据分析能力的培养,而在此过程中,学生的运算能力及符号意识也扮演者较为重要的角色.
4.5 关注概念表征的性别差异
男、女生在数学概念表征方式上存在差异,男生更倾向于结构表征,女生则更倾向于其它方面的表征.这在一定程度上反应了男、女生数学学习策略上的差异,前者注重体系建构,后者注重概念内部的多元理解.为此,教师应能适应男、女生在概念表征及理解上的差异,针对不同的学习人群进行适当的差异教学.
5 结论
八年级学生数学概念表征得分排序从高到低依次是符号表征、语言表征、图象表征及结构表征;上述排序在各地区之间、不同性别之间均没有差异.
男生结构表征显著优于女生,女生在其它表征方面均显著优于男生.
结构表征对数学学业成绩的直接影响及间接影响均达显著,直接影响贡献小于间接影响;各间接影响路径差异显著,通过符号表征的影响最大,通过语言表征的影响次之.
概念表征对三大内容领域的影响机制存在差异.在“数与代数”领域,结构表征对该领域成绩的直接影响及间接影响均达显著,二者贡献相当;间接影响路径差异显著,通过符号表征的影响最大,通过语言表征的影响次之.在“图形与几何”领域,结构表征对该领域成绩的直接影响及间接影响均达显著,且直接影响贡献小于间接影响;仅通过符号表征及语言表征的影响显著,且两条路径之间差异显著,前者大于后者.在“统计与概率”领域,仅间接影响达到显著;在间接影响中,仅通过符号表征及语言表征的影响显著,且两条路径之间差异显著,前者大于后者.
[1] 艾森克,基恩.认知心理学(上册)[M].高定国,肖晓云,译.4版.上海:华东师范大学出版社,2004:361.
[2] 李善良.现代认知观下的数学概念学习与教学理论研究[D].南京:南京师范大学,2002:25.
[3] SCHNOTZ W, BANNERT M. Construction and interference in learning from multiple representations [J]. Learning and Instruction, 2003, 13(2): 141-156.
[4] BRUNER J S. Toward a theory of instruction [M]. Cambridge, MA: Belknap Press, 1966: 4-20.
[5] LESH R, POST T, BEHR M. Representations and translations among representations in mathematics learning and problem solving [C] // Janvier C. Problems of representations in the teaching and learning of mathematics. Hillsdale, Nj: Lawrence Erlbaum Associates, 1987: 33-40.
[6] National Council of Teachers of Mathematics. Principles and standards for school mathematics [M]. Reston, VA: Author, 2000: 17.
[7] KELLER B A, HIRSCH C R. Student preferences for representations of functions [J]. International Journal of Mathematical Education in Science and Technology, 1998, 29(1): 1-17.
[8] 中华人民共和国教育部.全日制义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:12-24.
[9] 唐剑岚.国外关于数学学习中多元外在表征的研究述评[J].数学教育学报,2008,17(1):30-34.
[10] 罗新兵,罗增儒.数学概念表征的初步研究[J].数学教育学报,2003,12(2):21-23.
[11] 李善良.关于数学概念表征层次的研究[J].数学教育学报,2005,14(4):35-37.
[12] 徐速.数学问题解决中视觉空间表征研究的综述[J].数学教育学报,2006,15(1):35-38.
[13] 章佳颖.4~6岁儿童数学认知中的多元表征研究[D].上海:华东师范大学,2011:23-60.
[14] 孙雪梅,赵永香,朱维宗,等.云南民族地区六年级彝族学生数学问题解决表征水平的调查研究[J].数学教育学报,2016,25(3):85-92.
[15] 宋广文,李晓芹,朱振菁.小学儿童数字线估计的心理表征模式[J].数学教育学报,2013,22(5):52-56.
[16] 谢海燕,姜慧慧,张晋宇,等.我国八年级学生数学表征能力的调查研究[J].基础教育,2016,13(1):65-70.
[17] 程龙海,黄兴丰.中学生数学解题表征的一次调查测试[J].数学教育学报,2003,12(2):63-65.
[18] 文萍.高中生数学概念表征的调查研究[D].长春:东北师范大学,2007:14-28.
[19] 徐学兵.高中生数学符号语言表征能力的调查研究[D].南京:南京师范大学,2015:16-49.
[20] 喻平.不同年级中学生对数学问题表征的差异性研究[J].应用心理学,2005,11(6):110-115.
[21] 郭萌,熊妍茜,杨新荣,等.五年级和六年级学生分数表征转化能力的调查研究[J].数学教育学报,2016,25(5):49-54.
[22] 刘建新.高一学优生与普通生数学问题表征的差异研究[D].石家庄:河北师范大学,2016:19-30.
[23] 任莎莎.京族汉族小学生数学概念表征的调查研究[D].桂林:广西师范大学,2010:20-30.
[24] 张维,蔡笑岳,曾苑霞.学科领域知识丰富性对中学代数问题表征层次的影响[J].心理科学,2011,34(2):398-401.
[25] 邢强,单永明.数学应用题外部表征的影响因素及启发[J].数学教育学报,2012,21(5):19-22.
[26] 张睆,辛自强,陈英和,等.集合关系特征对小学生分数乘法应用题表征的影响[J].数学教育学报,2016,25(1):43-46.
[27] GARRETT L E. Theeffect of technological representations on developmental mathematics students’ understanding of functions [D]. Auburn, AL: Doctoral Dissertation of Auburn University, 2010: 169-172.
[28] HAISTINGS J L. Using virtual manipulatives with and without symbolic representation to teach first grade multi-digit addition [D]. Lawrence, NY: Doctoral Dissertation of University of Kansas, 2009: 27-51.
[29] 邢强,蔡新华,单永明.外部表征和问题呈现方式对小学生数学应用题解决的影响[J].数学教育学报,2014,23(4):74-77.
[30] 魏丽圆.数学表征对解高考解答题的影响研究[D].广州:华南师范大学,2015:7-23.
[31] 滕静.儿童非符号数量表征与数学学业成绩的关系[D].上海:华东师范大学,2015:40-50.
[32] 赵平.儿童数字空间表征发展及其与数学学业能力的关系研究[D].石家庄:河北师范大学,2015:15-17.
[33] 杜青霞.高中生数学概念多元表征的调查研究[D].武汉:华中师范大学,2014:8-10.
[34] 鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:129-136.
[35] VARGHESE T. Concept maps to assess student teachers’ understanding of mathematical proof [J]. The Mathematics Educator, 2009, 12(1): 49-68.
[36] MUTODI P, CHIGONGA B. Concept map as an assessment tool in secondary school mathematics: an analysis of teachers’ perspectives [J]. Eurasia Journal of Mathematics, Science & Technology Education, 2016, 12(10): 2 685-2 696.
[37] CHEN W, LIN H, NIEN S. The learning effectiveness of the concept map approach of e-learning applied to a math class of special educational students in a vocational school [J]. International Journal of Information and Education Technology, 2014, 4(5): 388-393.
[38] STEKETEE S, SCHER D. Connecting functions in geometry and algebra [J].Mathematics Teacher, 2016, 109(6): 448-455.
[39] MARGARET M. Using concept maps to show connections in measurement: an example from the australian curriculum [J]. Australian Mathematics Teacher, 2014, 70(4): 11-20.
[40] SUN X. “Variation problems” and their roles in the topic of fraction division in chinese mathematics textbook examples [J]. Educational Studies in Mathematics, 2011, 76(1): 65-85.
[41] 鲍建生,黄荣金,易凌峰,等.变式教学研究[J].数学教学,2003(1):11-12.
[42] TIMSS & PIRLS International Study Center. TIMSS 2011 assessment framework [R]. TIMSS & PIRLS International Study Center Lynch School of Education Boston College Publishing, 2009: 49-51.
[43] OECD. PISA 2012 assessment and analytical framework [M]. Washington, D. C. : OECD Publishing, 2013: 24.
[44] 綦春霞,张新颜,王瑞霖.八年级学生数学学业水平的现状及其影响因素研究[J].教育学报,2015,11(2):87-92.
[45] 张庆林,管鹏.小学生表征应用题的元认知分析[J].心理发展与教育,1997,13(3):11-14.
[46] CLEAVES W P. Promoting mathematics accessibility through multiple representations jigsaws [J]. Mathematics Teaching in the Middle School, 2008, 13(8): 446-452.
[47] GAGATSIS A, SHIAKALLI M. Ability to translate from one representation of the concept of function to another and mathematical problem solving [J]. Educational Psychology, 2004, 24(5): 645-657.
[48] VERONICA J D. Switching between memory and perception: moving attention or memory retrieval [J]. Memory & Cognition, 1990, 18(2): 119-127.
[责任编校:周学智]
Eighth Graders’ Mathematical Conceptual Representation and Its Impact Mechanism on Academic Performance: Large-Scale Test in Z Province
HE Sheng-qing1, QI Chun-xia1, 2
(1. Faculty of Education, Beijing Normal University, Beijing 100875, China;2.Beijing Advanced Innovation Center for Future Education, Beijing 100875, China)
The present large-scale test chose 34 412 eighth graders from Z province as the subjects to investigate mathematical conceptual representation and its impact mechanism on academic performance. The results shown that eighth graders’ propensity of conceptual representation from high to low was symbolic representation, pictorial representation, linguistic representation and structural representation; Males shown preference to structural representation while females tend to others; The indirect impact mediated by other representations from structural representation to mathematics score and three content scores were both significant, and the effect size was bigger than direct impact; Among the indirect impact paths, the effect size was highest when mediated by symbolic representation, and linguistic representation followed; The impact mechanism was different among different content areas. Suggestions to curriculum and instruction were that, to cultivate students’ ability of multiple representation and the transformation among them; To help students constructing their own mathematics system; To attach attention to the symbols consciousness and mathematical communication ability; To pay attention to the influential path among different content areas; To pay attention to gender difference in conceptual representation.
eight graders; symbolic representation; pictorial representation; linguistic representation; structural representation; academic performance
G622.0
A
1004–9894(2017)06–0060–07
何声清,綦春霞.八年级学生数学概念表征及其对学业成绩的影响机制——基于Z省的大规模测试[J].数学教育学报,2017,26(6):60-66.
2017–06–04
北京师范大学未来教育高精尖创新中心项目——中学数学学科诊断分析工具开发与应用研究(BJAICFE2016SR-008);2016年国家建设高水平大学公派研究生项目(留金发[2016]3100);中国基础教育质量监测协同创新中心“区域质量健康体检项目”子项目——中学数学学业质量诊断与反馈(105006)
何声清(1988—),男,安徽安庆人,博士生,主要从事数学教育研究
