基于测试的高中生数学抽象素养水平现状研究

郑雪静，陈清华，王长平



基于测试的高中生数学抽象素养水平现状研究

郑雪静1，2，陈清华1，王长平1

（1．福建师范大学 数学与信息学院，福建 福州 350117；2．泉州师范学院 数学与计算机科学学院，福建 泉州 362000）

数学抽象素养是6个数学核心素养之一．通过建构一个数学抽象素养水平评价框架，利用自编的数学抽象素养水平测试卷，对福建省高中生数学抽象素养水平现状进行研究．结果表明：（1）高中生数学抽象素养水平一般；（2）高二与高三学生数学抽象素养水平存在显著差异；（3）高中男生与女生数学抽象素养水平存在显著差异；（4）市区、县城、乡镇不同地域学生数学抽象素养水平不均衡．

数学抽象素养；高中生；测试；评价

1 引言

自20世纪90年代以来，“核心素养”成为国际的重要议题．2014年3月30日，中国教育部印发的《关于全面深化课程改革，落实立德树人根本任务的意见》中指出：研究制订学生发展核心素养体系，明确学生应具备适应终身发展和社会发展需要的必备品格和关键能力．该《意见》正式提出“核心素养体系”的概念[1]．2016年9月13日发布的《中国学生发展核心素养》中指出：学生发展核心素养指学生应具备的，能够适应终身发展和社会发展需要的必备品格和关键能力，是关于学生知识、技能、情感、态度、价值观等多方面要求的综合表现[2]．至此，关于核心素养的研究引起了教育界的广泛关注．普通高中数学课程标准修订组专家提出高中6个数学核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析[3]，并分别对这6个核心素养从内涵、价值、表现3个方面进行描述，同时分别从情境与问题、知识与技能、思维与表达、交流与反思4个方面对6个核心素养进行3个水平的划分．

修订的《普通高中数学课程标准》即将颁布，如何对接高考综合改革？在“素养立意”命题理念下，如何评价高中生的数学核心素养水平？对这些问题的研究已迫在眉睫．数学抽象素养是第一个数学核心素养，通过建构一个数学抽象素养水平评价框架，利用自编的数学抽象素养水平测试卷，对福建省高中生数学抽象素养水平现状进行研究，以期为高中生数学核心素养水平的评价研究提供借鉴．

2 理论基础

2.1 数学核心素养的相关研究

许多学者对数学核心素养进行了相关研究[4-6]，南京师范大学喻平教授对数学学科核心素养要素析取进行实证研究，并提出将数学核心素养划分为知识理解、知识迁移、知识创新3种水平的评价框架．天津师范大学王光明教授等对高中生数学素养的操作定义进行了研究．2017年《数学教育学报》第1期刊载了7篇[7-13]基于2016年江苏省八年级学生学业质量监测的数学核心素养发展状况研究的文章，其借鉴高中数学核心素养水平划分，将初中数学核心素养的具体表现进行4个水平的划分，进而对不同群体分别就质量监测中与6个数学核心素养相关的题目得分情况及水平分布进行统计分析，得出江苏省八年级学生6个数学核心素养相应发展水平的特征．然而，目前对高中生数学核心素养水平的测评研究还很欠缺．

2.2 数学抽象素养的理解

数学抽象素养是6个数学核心素养之一，《普通高中数学课程标准（征求意见稿）》从内涵、价值、表现对其进行了描述．数学抽象是指舍去事物的一切物理属性，得到数学研究对象的素养．它主要包括：从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系，从事物的具体背景中抽象出一般规律和结构，用数学语言予以表征．数学是研究现实世界的数量关系和空间形式，因此，数学抽象主要是从众多事物中抽取出其在数量和图形方面共同的、本质的特征，通过对数量与图形的性质、关系和规律进行研究，进而用数学符号进行表征．

数学发展本质上依赖于抽象、推理、模型3个思想，其中最核心的是抽象思想[14]．数学抽象使得数学具有一般性．史宁中教授认为，数学抽象从表现形态和思维形态来看，需要经历两次抽象[15]，第一次是概念抽象，是在基于现实的概念抽象基础上，进而基于逻辑的抽象，从而得到数学概念以及概念之间的性质、关系和规律；第二次抽象是符号抽象，其抽象的特点是符号化、形式化和公理化．数学抽象让学生经历由感性具体到理性具体，从理性具体上升为理性一般的思维过程．

通过高中数学课程的学习，学生能在情境中抽象出数学概念、命题、方法和体系，积累从具体到抽象的活动经验；养成在日常生活和实践中一般性思考问题的习惯，把握事物的本质，以简驭繁；运用数学抽象的思维方式思考并解决问题．也即，学生形成一定的数学抽象素养，能够用数学的眼光观察现实世界，运用数学抽象的方法抓住事物的本质和结构，在一般的、抽象的层面上思考问题．同时，在数学学习过程中，能够更好地理解数学、应用数学，以及形成数学化的能力和思维习惯．

2.3 数学抽象素养水平评价框架

要评价高中生的数学抽象素养水平，首先要构建评价框架．依据《普通高中数学课程标准（征求意见稿）》中关于数学抽象素养3个水平的划分，同时借鉴PISA的数学能力群[16]，构建了一个数学抽象素养水平的评价框架（见表1）．评价框架里涉及6个指标，包括3个内容维度和3个水平维度．内容维度为：（1）情境：包含熟悉的情境、关联的情境、综合的情境；（2）认知：包含的行为动词有了解、模仿、理解、感悟、掌握（能）、建构、运用和创新；（3）表达：包括书面表达或口头表达，是交流过程中的思维表现和思维结果，包含的行为动词是解释．水平维度为：（1）再现（Reproduction Cluster）：主要指能够在熟悉的情境中结合相应的数学概念和规则，模仿学过的常规方法解决问题，包括常规的计算、推理和表达；（2）联系（Connections Cluster）：主要指能够在关联的情境中，对所学知识进行整合、关联以及适当拓展，能够对常规问题解决进行转换和解释，甚至运用多种方法进行计算、推理、论证，包括建模，提炼出通性通法；（3）创造（Creation Cluster）：主要指能够在综合情境中发现和提出数学问题，创造解决数学问题的新方法，包括建模，解决复杂问题．

表1 数学抽象素养水平评价框架

3 研究设计

3.1 研究思路

采用质性与量化相结合的研究方法，质性研究是结合文献对数学抽象素养的内涵进行界定，并建构一个数学抽象素养水平评价框架；量化研究是在质性分析的基础上通过自编测试卷，基于测试对福建省高中生数学抽象素养水平现状进行研究．

3.2 研究对象

以高二、高三学生为研究对象，采用分类和整群相结合的随机抽样方法，发放问卷量及回收样本量比较大，覆盖面比较广，包括福州、莆田、泉州、厦门、三明、龙岩地区的高中学校，既有市区中学，也有县城、乡镇中学，具有一定的代表性．共收回有效问卷3 704份：高二2 571份，其中女生1 304份，男生1 267份；高三1 133份，其中女生610份，男生523份．具体地区样本量和所占比例见图1．

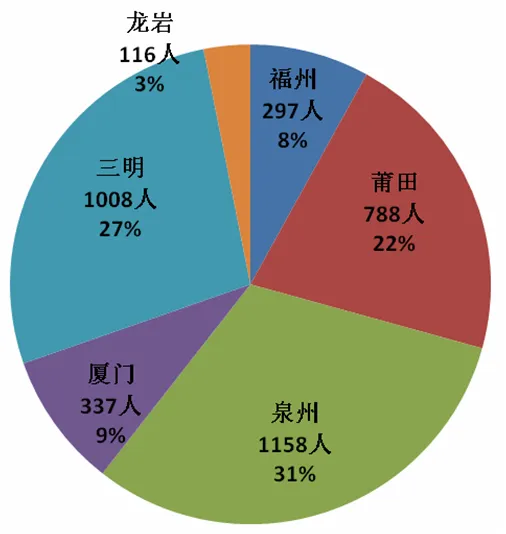
图1 样本地区分布

3.3 研究工具

（1）试卷编制．

史宁中教授认为：核心素养是后天习得的，与特定情境有关，是通过人的行为表现出来的，因此是可监测的知识、能力和态度[17]．关于数学抽象素养水平测试卷的编制，试题命制以《普通高中数学课程标准（征求意见稿）》中关于命题的建议为指导，综合考虑3个层面：一是3个基本要素：问题与情境、知识与技能、思维与表达；二是3条内容主线：函数、几何与代数、数学建模活动与数学探究活动；三是数学抽象素养的3个水平：水平一、水平二、水平三．进而选取与数学抽象素养相关联的知识，与现实生活及其它学科相联系的情境，聚焦数学概念、定理、方法、思想的理解和应用，淡化解题技巧，以知识内容为基础，思想方法为舵手，能力意识为根本，核心素养为目标，重点考查学生的数学抽象素养．测试题目的数学抽象素养水平是以表1评价框架为标准设置的，是经过十多名研究生多轮讨论，同时综合一线教师和多位专家的意见，有往年高考原题或拓展题，有改编、自编的试题，最终确定了9道与数学抽象素养相关的测试题，附加一道以“数学抽象”为题的写作题，总测试时间为150分钟．另外，为了避免学生由于知识水平不足对测试带来的影响，选择的测试时间段是高二、高三下半学期，测试的知识水平没有超过该时间段之前的课程内容要求．（测试卷详见附件）

（2）测试题目水平分析．

测试题水平分布为：第1题、第2题、第3题、第4题、第9题（Ⅰ）（Ⅱ）归属水平一类型；第5题、第6题、第7题、第8题、第9题（Ⅲ）归属水平二类型；第9题（Ⅳ）归属水平三类型．下面仅以一道试题为例就数学抽象素养水平二进行分析，见表2．

表2 数学抽象素养水平二试题分析

（3）水平等级细分．

进一步采用四等级细分法，将水平一、水平二、水平三各细分为、、、四个等级．测试卷中选择题、填空题的分值分别为3分、4分，水平一、水平二、水平三的解答试题分值分别为6分、9分、12分．将数学抽象素养水平一的试题得分为0分的定为等级，得分1~2分定为等级、得分3~4分定为等级，得分5~6分定为等级；将水平二的试题得分为0分的定为等级，得分1~3分定为等级、得分4~6分定为等级，得分7~9分定为等级；将水平三的试题得分为0分的定为等级，得分1~4分定为等级、得分5~8分定为等级，得分9~12分定为等级（见表3）．

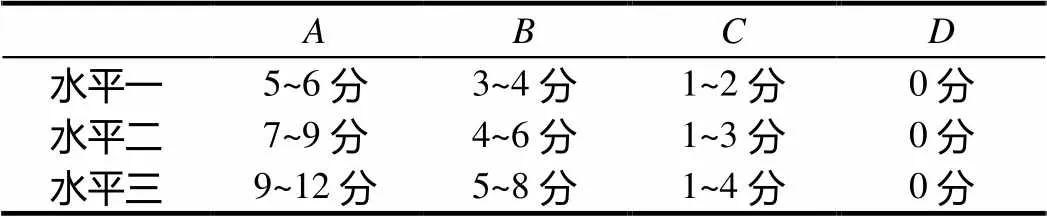
表3 水平等级细分

4 研究结果统计与分析

在编制好测试题及进行等级细分之后，制定了试题的评分标准．通过对研究对象的测试，由十多位研究生对收回的3 704份有效测试卷进行初评，最后由作者进行一一复评，当初评与复评分数出现不一致时，再经讨论确定分数并将成绩录入．录入前先对试卷进行7位编码：地区、学校、年级（编码2为高二、编码3为高三）、性别（编码1为女生、编码2为男生）、三位数编号，如泉州五中高二年级女生第10份试卷编码：CW21010．采用IBM SPSS Statistics 22 统计软件进行数据分析．

4.1 试卷信度分析

对3 704份样本在9道测试题（14个分题）中所得总分进行信度分析，采用信度系数的内部一致性信度分析，结果显示：测试卷的信度系数为0.841，具有非常好的信度[18]，说明这份测试卷测试结果具有较强的可靠性（详见表4）．

表4 信度分析

4.2 试题的难度与区分度分析

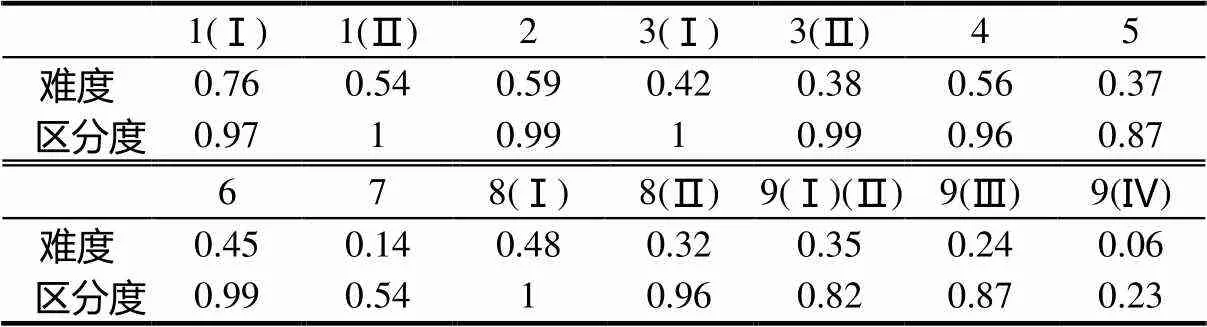
表5 试题的难度和区分度

表5显示，水平三试题第9题（Ⅳ）难度最大，难度值为0.06；从解答题的角度看，水平一试题第1（Ⅱ）题、第2题、第4题难度中等，难度值分别为0.54、0.59、0.56，而第3（Ⅱ）题、第9题（Ⅰ）（Ⅱ）难度值分别为0.38、0.35，测试结果比预测的难度略大；水平二试题第5题、第7题、第8（Ⅱ）题、第9题（Ⅲ）难度值分别为0.37、0.14、0.32、0.24，难度较大，第6题难度中等，而第7题难度超出了预测水平．整个试卷的难度采用各题难度与分值权重的乘积再求和的方法计算，试卷难度系数为0.35，试卷总体难度比较大．对于区分度，第9（Ⅳ）区分度为0.23，具有一定的区分功能，其它试题都具有很好的区分功能．整个试卷的区分度采用各题区分度与分值权重的乘积再求和的计算方法，试卷区分度为0.82，具有很好的区分度．

4.3 高中生数学抽象素养水平等级分析

利用表3的水平等级细分，对每道测试题得分的分布进行统计分析，借以分析学生的数学抽象素养水平等级分布情况．

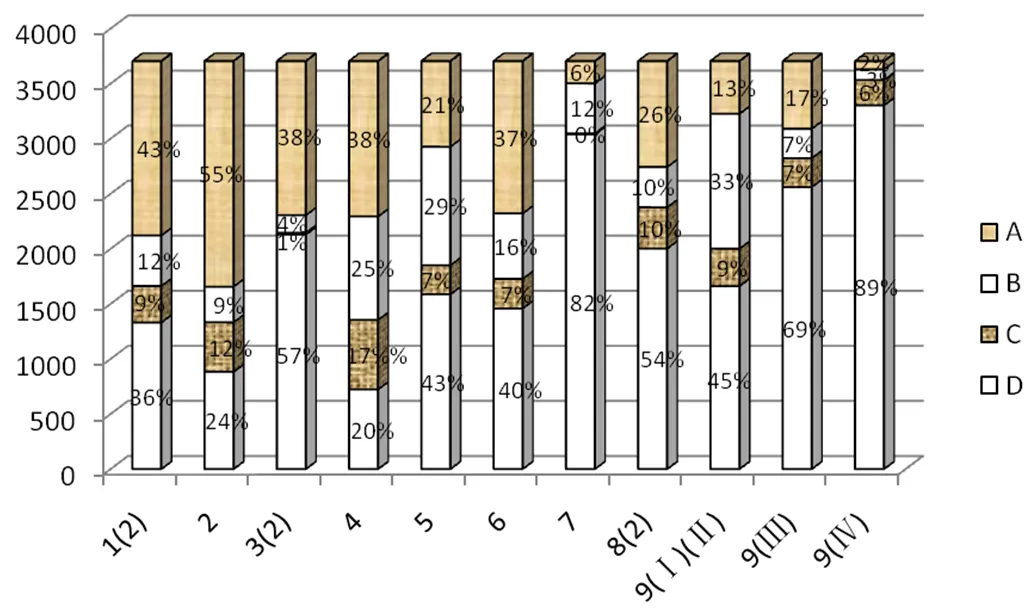
图2 学生数学抽象素养水平等级分布

图2显示各题中学生的数学抽象素养水平等级的百分比，其中考查水平一的第2题，学生达到等级的比重最大，有55%，最少的是第9题（Ⅰ）（Ⅱ），等级的比重为13%；将考查水平一的5道试题进行等级求和平均，得出学生数学抽象素养处于水平一、、、等级的比例分别为：37%、17%、10%、36%．考查水平二的试题中，学生达到等级比重最大的是第6题，有37%，最少的是第7题，仅6%；将考查水平二的5道试题进行等级求和平均，处于、、、等级的比例分别为：21%、15%、6%、58%．考查水平三的第9题（Ⅳ），学生数学抽象素养水平处于、、等级的比例分别为2%、3%、6%，而处于等级的有89%．

4.4 差异显著性检验

（1）高二、高三学生数学抽象素养水平差异显著性检验．对高二、高三学生数学抽象素养水平测试成绩进行独立样本检验．结果如表6、表7所示．

表6 基本描述性统计量

表7 独立样本t检验结果

（2）高中男、女生数学抽象素养水平差异显著性检验．

分别对高二和高三的男生与女生数学抽象素养水平测试成绩进行独立样本检验．结果如表8、表9所示．

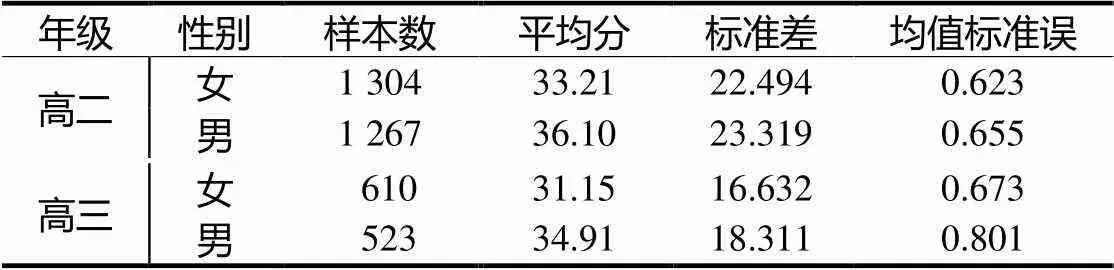
表8 基本描述性统计结果

表9 独立样本t检验结果

（3）市区、县城、乡镇差异显著性检验．

将调查的学校以市区、县城、乡镇归为3类，采用单因素方差分析，对这3类学校高二学生的数学抽象素养水平进行差异显著性分析．具体见表10—表13．

表10 描述统计量

表11 方差齐性检验

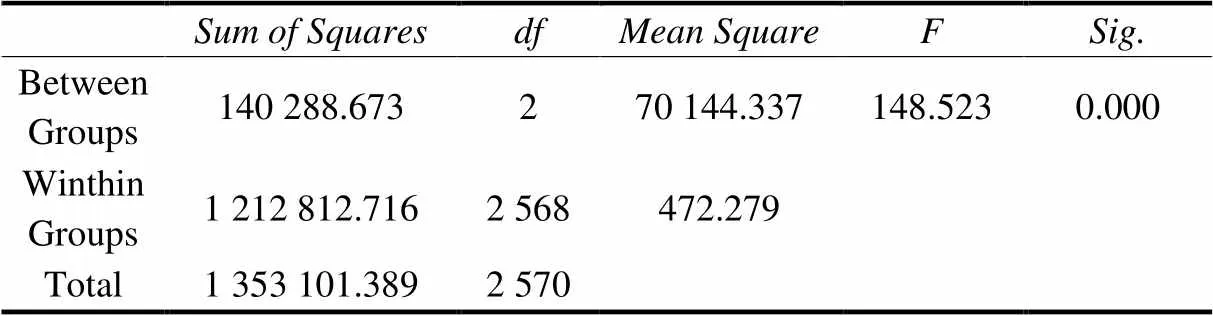
表12 方差分析

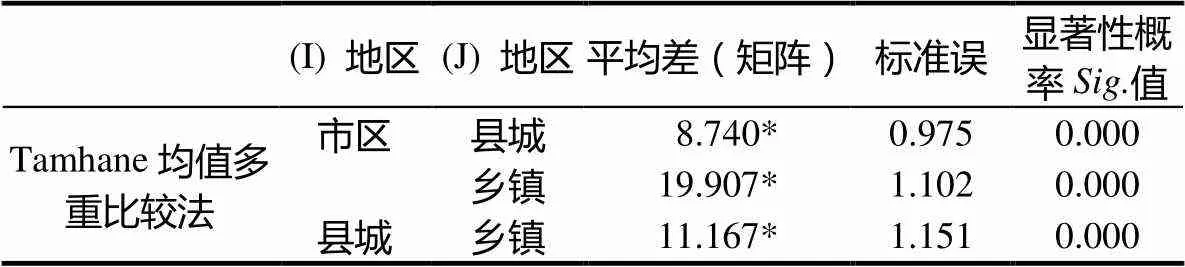
表13 均值多重比较

5 结论

通过测试数据分析，福建省高中生数学抽象素养水平现状如下：

（1）学生数学抽象素养水平一般．达到水平一、水平二等级的学生分别只有37%、21%，而处于水平二、水平三等级的学生分别有58%、89%．

（2）高二与高三学生数学抽象素养水平存在显著差异，总体上高二学生数学抽象素养的平均水平比高三学生高．

（3）高中男生与女生数学抽象素养水平存在显著差异，总体上高中男生数学抽象素养的平均水平比高中女生高．

（4）市区、县城、乡镇不同地域学生数学抽象素养水平不均衡．总体上，市区学生数学抽象素养的平均水平比县城高，县城学生数学抽象素养的平均水平比乡镇高．

6 反思与建议

（1）数学抽象一般是在熟悉的、关联的或综合的情境中进行，涉及一定的情境阅读，尤其是在关联的、综合的情境中，需要学生具备一定的阅读理解能力，阅卷中发现学生的阅读理解能力有待进一步提高．要提高学生的数学抽象素养水平，教师需要在一定程度上加强学生数学阅读理解能力的提升．

（2）高二学生数学抽象素养的平均水平比高三学生高．对于这一现象，可以从以下多方面进行反思：一方面，从试卷作答情况以及对部分学校高三学生的访谈发现，学生反映测试时正值高三紧张复习时期，因此，部分学生对测试卷作答积极性不够；另一方面，在应试训练及解题训练的背景下，高三阶段对学生素养培养的关注度可能有些欠缺；第三，建立的评价指标的科学性还有待进一步的实践检验．

（3）文[8]研究结果表明在数学抽象能力的发展上，初二年级男女学生基本不存在显著差异．研究结果显示，高二男女生数学抽象素养水平存在显著差异．这种差异是随着年级的升高导致呢，还是受其它因素的影响？这是一个值得进一步研究的课题．

（4）学生的数学抽象素养水平存在地域间的显著差异．那么，学生的其它5个数学核心素养水平是否也存在地域间的差异？高考数学命题经历“知识立意”到“能力立意”再到即将到来的“素养立意”的演变，“素养”理念下的数学教育如何缩短地域差异？这是需要整个教育部门认真思考的问题．

（5）虽然整个测试卷具有很好的区分度，但个别试题测试结果超出了预设难度．如何控制试题难度，更好地评价学生的数学抽象素养水平，需要更多的实践检验．

（6）6个数学核心素养既相互独立，又相互交融，尽管测试题侧重考查学生的数学抽象素养水平，但其它数学核心素养是否会影响数学抽象素养水平的考查，这里的研究尚未涉及，期待在后续测评研究中进一步加以完善．

致谢：感谢东北师范大学史宁中教授莅临福建师范大学讲学带来的启示与思考；感谢2016年全国教育科学规划课题“高中生数学核心素养培养的策略及评价研究”对研究的推动作用；感谢参与调查研究的17所学校；感谢福建师范大学陈清华教授指导的十多位在读研究生在试卷批改过程中的帮助．

[1] 中华人民共和国教育部．关于全面深化课程改革落实立德树人根本任务的意见[EB/OL]．（2014-04-24）[2017-02-20]．http://www.snedu.gov.cn/news/qitawenjian/201404/24/7873.html.

[2] 中华人民共和国教育部．《中国学生发展核心素养》发布[EB/OL]．（2016-09-14）[2017-02-20]．http://edu.people. com.cn/n1/2016/0914/c1053-28714231.html.

[3] 洪燕君，周九诗，王尚志，等．《普通高中数学课程标准（修订稿）》的意见征询——访谈张奠宙先生[J]．数学教育学报，2015，24（3）：35-39．

[4] 喻平．数学学科核心素养要素析取的实证研究[J]．数学教育学报，2016，25（6）：1-6．

[5] 王光明，张楠，周九诗．高中生数学素养的操作定义[J]．课程·教材·教法，2016，36（7）：50-55．

[6] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19-23，59．

[7] 董林伟，喻平．基于学业水平质量监测的初中生数学核心素养发展状况调查[J]．数学教育学报，2017，26（1）：7-13．

[8] 殷容仪，赵维坤．基于质量监测的初中学生数学抽象发展状况的调查研究[J]．数学教育学报，2017，26（1）：14-15，63．

[9] 周雪兵．基于质量监测的初中学生逻辑推理发展状况的调查研究[J]．数学教育学报，2017，26（1）：16-18．

[10] 李贺，张卫明．基于质量检测的初中学生数学建模发展状况的调查研究[J]．数学教育学报，2017，26（1）：19-21，87．

[11] 徐德同，钱云祥．基于质量监测的初中学生直观想象发展状况的调查研究[J]．数学教育学报，2017，26（1）：22-24．

[12] 杭毅，侯正永．基于质量监测的初中学生数学运算发展状况的调查研究[J]．数学教育学报，2017，26（1）：25-27．

[13] 张爱平，马敏．基于质量监测的初中学生数据分析发展状况的调查研究[J]．数学教育学报，2017，26（1）：28-31．

[14] 史宁中．数学思想概论：第1辑——数量与数量关系的抽象[M]．长春：东北师范大学出版社，2008：1．

[15] 史宁中．数学思想概论：第5辑——自然界中的数学模型[M]．长春：东北师范大学出版社，2015：2-3．

[16]  OECD Publishing. PISA 2012 assessment and analytical framework: mathematics, reading, science, problem solving and financial literacy [M]. Oecd Publishing, 2013: 264.

[17] 史宁中．学科核心素养的培养与教学——以数学学科核心素养的培养为例[J]．中小学管理，2017（1）：35-37．

[18] 吴明隆．问卷统计分析实务——SPSS操作与应用[M]．重庆：重庆大学出版社，2010．

附录：高中生数学核心素养之“数学抽象”测试卷

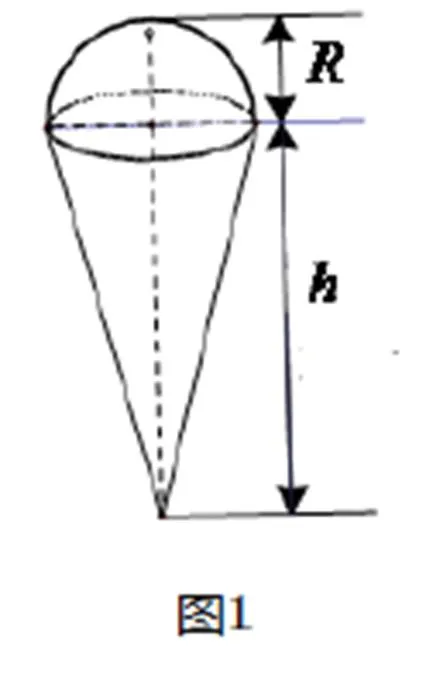
2．一个圆锥形的空杯子上放一个半径为的半球形冰淇淋（如图1），请你设计一种这样的圆锥形杯子（杯口直径等于半球形的冰淇淋的直径，杯子壁厚度忽略不计），使冰淇淋融化后不会溢出杯子，怎样设计最省材料？（说明：液体与固体的密度差忽略不计）

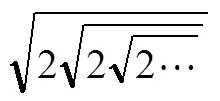
4．某新型企业随市场竞争加剧，为获得更大利润，企业须不断加大投资，若预计年利润率低于10%时，则该企业就得考虑转型．下表显示的是某企业从2013—2016年四年来年利润（百万）与年投资成本（百万）变化的一组数据．

年份2013201420152016…… 投资成本x（百万）35917…… 年利润y（百万）1234……

（Ⅰ）请根据上表的数据，选择一个适当的函数模型来描述年利润与投资成本的变化关系，并给出你选择的理由．

（Ⅱ）若要使企业利润超过6百万，则该企业就得考虑转型，这句话对不对？为什么？

5．学习了等差数列、等比数列之后，你是否想过还存在等和数列、等积数列？如果存在，请给出等和数列和等积数列的定义，并写出等和数列和等积数列各项的特点．

6．某时刻点向西400千米的处是台风中心，台风以每小时40千米的速度向东北方向直线前进，以台风中心为圆心、300千米为半径的圆称为“台风圈”，从此时刻算起，经过多长时间点进入台风圈？点处在台风圈中的时间多长？

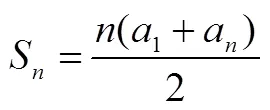
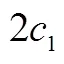
其中正确式子的序号是，请写出解答过程．

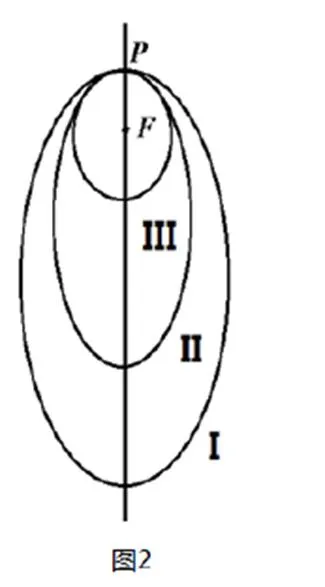
A. ①③ B. ①④ C. ②③ D. ②④

10．写作题：请以“数学抽象”为题，举例说明你对“数学抽象”的认识．（可以通过语言、文字、符号、图像综合阐述，200字左右．）

[责任编校：周学智]

Based Testing Research on the Current Situation of High School Students’ Level about Mathematics Abstract Literacy

ZHENG Xue-jing1, 2, CHEN Qing-hua1, WANG Chang-ping1

(1. School of Mathematics and Informatics, Fujian Normal University, Fujian Fuzhou 350117, China;2. School of Mathematics and Computer Science, Quanzhou Normal University, Fujian Quanzhou 362000, China)

Mathematical abstract literacy was one of the six mathematics key competencies. By constructing a evaluation framework of mathematical abstract literacy, using the self-made mathematical abstract literacy test volume, this paper made a research on the current situation of senior high school students’ mathematics abstract literacy in Fujian province. The results showed that: (1) Senior high school students’ mathematical abstract literacy level were general. (2) There were significant differences in the level of mathematical abstract literacy between senior two and senior three students. (3) There were significant differences in the level of mathematical abstract literacy between high school boys and girls. (4) The level of students’ mathematical abstract literacy was unbalanced between urban area, county town and village town.

mathematics abstract literacy; high school students; test; evaluation

G632

A

1004–9894（2017）06–0026–07

郑雪静，陈清华，王长平．基于测试的高中生数学抽象素养水平现状研究[J]．数学教育学报，2017，26（6）：26-32．

2017–05–24

2016年全国教育科学规划课题——高中生数学核心素养培养的策略及评价研究（DHA160364）；2015年福建省中青年教师教育科研项目——基于微课建设的高等数学课程改革理论与实践研究（JAS150461）

郑雪静（1978—），女，福建泉州人，讲师，博士生，主要从事数学教育、考试命题与评价研究．